
1.Понятие множества. Элементы множества
будем считать множество заданным, если его элементы однозначно определены и это не приводит к каким либо противоречиям.
Множества бывают конечными и бесконечными.
Конечное множество – множество, содержащее конечное число элементов
Бесконечное множество – множество, содержащее бесконечное число элементов.
Существует 2 способа задания множеств:
-
Перечисление элементов.
В таком случае элементы множества записываются в фигурных скобках через запятую. В случае бесконечных множеств можно указать интуитивно ясную последовательность и поставить многоточие.
Последний пример – бесконечное множество чисел, делящихся без остатка на 4.
-
Описание характеристического свойства элементов.
В этом случае используют следующий макет: {x | x обладает свойством Р}.
Объекты, из которых состоит множество, называют элементами множества Множества чаще всего обозначают большими буквами латинского алфавита, его элементы — маленькими Если а не является элементом множества А, то записывают а ∉ А В отличие от мультимножества каждый элемент множества уникален, и в множестве не может быть двух идентичных элементов: {6, 11} = {11, 6} = {11, 11, 6, 11}
2.Операции над множествами
Существует несколько основных операций над множествами.
-
Выделение подмножества.
Множество
А называется подмножеством
множества В, если любой элемент из
множества А является элементом множества
В. Это обозначается
 или
или
 .
Замечание:
Разумеется, любое множество является
подмножеством для самого себя. Такое
подмножество называется собственным
подмножеством.
.
Замечание:
Разумеется, любое множество является
подмножеством для самого себя. Такое
подмножество называется собственным
подмножеством.
-
Объединение множеств.
Множество
С, состоящее из всех элементов,
принадлежащих хотя бы одному из данных
множеств А и В называется объединением
множеств А и В и обозначается
 .
.
3.Пересечение множеств.
Множество
С, состоящее из всех элементов,
принадлежащих сразу двум множествам А
и В называется пересечением
множеств А и В и обозначается
 .
.
4.Разность множеств.
Множество С, состоящее из всех элементов, принадлежащих множеству А и одновременно не принадлежащих множеству В называется
разностью
между множеством А и множеством В и
обозначается
 .
.
5.Симметрическая разность.
Множество
С, состоящее из всех элементов,
принадлежащих только одному из данных
множеств называется симметрической
разностью
между множеством А и множеством В и
обозначается
 .
.
6.Универсальное множество.
Универсальным множеством или универсумом называется объединение всех рассматриваемых в конкретной задаче множеств.
Пример:
7.Дополнение множества.
Пусть
U
– универсальное множество, а А –
некоторое множество, тогда
 будет называться дополнением
множества
А и обозначаться
будет называться дополнением
множества
А и обозначаться
 .
.
3.Декартово произведение множеств
декартово
произведение
двух множеств — множество,
элементами
которого являются всевозможные
упорядоченные пары элементов исходных
двух множеств. Отображения
произведения множеств в его множители
называют координатными
функциями.
Степенью декартового произведения
![]() называется
число множеств n, входящих в это декартово
произведение. Замечание.
Если все множества
называется
число множеств n, входящих в это декартово
произведение. Замечание.
Если все множества
![]() одинаковы,
то используют обозначение
одинаковы,
то используют обозначение
![]() .
.
4.Основные логические операции
В логике логическими операциями называют действия, вследствие которых порождаются новые понятия, возможно с использованием уже существующих.
 – тождественный
ноль;
– тождественный
ноль;
 – конъюнкция
(
– конъюнкция
( )
или
)
или
 .
.
 – тождественный
– тождественный

 – обратная
импликация
– обратная
импликация
 – тождественный
– тождественный

 – сумма
по модулю 2 (сумма Жегалкина) (
– сумма
по модулю 2 (сумма Жегалкина) ( )
)
 – дизъюнкция
(
– дизъюнкция
( )
)
 – стрелка
Пирса (отрицание дизъюнкции) (
– стрелка
Пирса (отрицание дизъюнкции) ( )
)
 – эквиваленция
(
– эквиваленция
( )
)
 – отрицание
– отрицание
 (не
(не
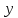 )
(
)
( )
)
 – отрицание
– отрицание
 (не
(не
 )
(
)
( )
)
 – импликация
(
– импликация
(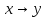 )
)
 – штрих
Шеффера (отрицание конъюнкции) (
– штрих
Шеффера (отрицание конъюнкции) (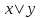 )
)
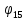 – тождественная
единица.
– тождественная
единица.
5.Таблица истинности. Представление логической функции формулой. Дизъюнктивная нормальная форма.
Таблица истинности — это таблица, описывающая логическую функцию.
Под «логической функцией» в данном случае понимается функция, у которой значения переменных и значение самой функции выражают логическую истинность.
Дизъюнкти́вная норма́льная фо́рма в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ.Для этого можно использовать закон двойного отрицания, закон де Моргана, закон дистрибутивности. Дизъюнктивная нормальная форма удобна для автоматического доказательства теорем.
Алгоритм построения днф
1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием
2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул
3) Избавиться от знаков двойного отрицания.
4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.
6. СДНФ, СКНФ. Способы приведения к СДНФ, СКНФ.
Совершенной дизъюнктивной нормальной формой называется такая дизъюнктивная нормальная форма, у которой в каждую конъюнкцию входят все переменные данного списка
Совершенная Конъюнктивная Нормальная Форма — это такая КНФ, которая удовлетворяет трём условиям:
-
в ней нет одинаковых элементарных дизъюнкций
-
в каждой дизъюнкции нет одинаковых пропозициональных букв
-
каждая элементарная дизъюнкция содержит каждую пропозициональную букву из входящих в данную КНФ пропозициональных букв.
Способы приведения к СДНФ.
1. Составить таблицу истинности для данной функции;
2. Для каждой строки таблицы, в которой функция принимает значение истина (1) выписать конъюнкцию переменных, записав переменную с отрицанием, если соответствующее ей значение в данной строке равно 0, в противном случае без отрицания.
3. Соединить все элементарные конъюнкции дизъюнкцией.
Способ приведения к СКНФ.
1. Составить таблицу истинности для данной функции;
2. Для каждой строки таблицы, в которой функция принимает значение ложь (0) выписать дизъюнкцию переменных, записав переменную с отрицанием, если соответствующее ей значение в данной строке равно 1, в противном случае без отрицания.
3. Соединить все элементарные дизъюнкции конъюнкцией.
7.Законы логики
-
Закон тождества
-
Закон исключённого третьего
-
Закон противоречия
-
Закон достаточного основания
-
Законы де Моргана
-
Законы дедуктивных умозаключений
-
Закон Клавия
-
Законы деления
8.Упрощение формул логики с помощью равносильных преобразований.
Под упрощением формулы понимают равносильное преобразование , приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных
9.Булевы векторы. Понятие булевой функции.
Булева функция— это функция, все аргументы и все значения которой принадле-жат множеству .
10.Представление булевой функции в виде МДНФ методом Квайна.
Метод Куайна — способ представления функции в ДНФ или КНФ с минимальным количеством членов и минимальным набором переменных. Преобразование функции можно разделить на два этапа:
-
на первом этапе осуществляется переход от канонической формы (СДНФ или СКНФ) к так называемой сокращённой форме;
-
на втором этапе — переход от сокращённой формы к минимальной форме.
11.Операция двоичного сложения. Многочлен Жегалкина.
Жегалкина многочлен) над Z2, то есть с коэффициентами вида 0 и 1, где в качестве произведения берется конъюнкция, а в качестве сложения исключающее или. Многочленом был предложен в 1927 году И. И. Жегалкиным в качестве удобного средства для представляения функций булевой логики
13. Важнейшие замкнутые классы.
Замкнутый класс в теории булевых функций — такое множество P функций алгебры логики, любая функция, которую можно выразить формулой с использованием функций множества P, снова входит в это же множество.
14..Основные понятия логики предикатов.
n-местный
предикат
– это отображение
 ,
где
,
где
 ,
а
,
а
 ,
элементы которого понимаются как «ложь»
и «истина». Множество
,
элементы которого понимаются как «ложь»
и «истина». Множество
 называется областью
определения
предиката и обозначается
называется областью
определения
предиката и обозначается
 .
.
0-местный предикат называется высказыванием.
Подмножество
области определения, состоящее из таких
наборов переменных, при которых предикат
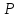 принимает значение 1, называется областью
истинности
предиката
принимает значение 1, называется областью
истинности
предиката
 и обозначается нами
и обозначается нами
 .
.
15.Логические операции над предикатами
Так как предикат принимает логические значения, то можно составлять логические формулы, переменными в которых будут предикаты. Эти формулы также будут предикатами. Часто их называют сложными предикатами.
16.Кванторные операции над предикатами
Квантор
(все-)общности
![]()
Квантор
существования
![]()
Квантор существования по переменной x1
Определение.
Операцией
связывания квантором общности
называется правило, по которому каждому
одноместному предикату Р(х), определенному
на множестве М, сопоставляется
высказывание, обозначаемое
![]() ,
которое истинно в том и только в том
случае, когда предикат Р(х) тождественно
истинен, и ложно в противном случае,
то есть
,
которое истинно в том и только в том
случае, когда предикат Р(х) тождественно
истинен, и ложно в противном случае,
то есть
17. Бинарные отношения. Свойства бинарных отношений.
В математике бинарным отношением называется подмножество декартова произведения двух множеств
