11. Основные равносильные формулы логики предикатов.

Пусть A(x) и B(x)  переменные предикаты, а C  переменное высказывание, тогда имеют место следующие равносильности:

1) ;

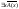2) ;

3) ;

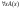
4) ;

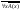5)

6) ;

7) ;

8) ;

9) .

10)

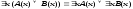
11) ;

12) ;

13) ;

14) .

15) ;

16) .

12. Предваренная нормальная форма формул логики предикатов.

В алгебре логики было введено понятие нормальной дизъюнктивной и конъюнктивной форм функции. В логике предикатов, сохраняя преемственность, используют аналогичное понятие для формул логики предикатов,отличающееся тем, что оно, кроме операций дизъюнкции, конъюнкции

и отрицания, распространяется и на кванторные операции и определяется следующим образом.

Определение. Нормальной формой формулы логики предикатов является такая формула, которая содержит только операции конъюнкции. дизъюнкции и кванторные операции, а операция отрицания применяется только к элементарным формулам. Под элементарной формулой понимается один отдельно взятый предикат.

Замечание. Иногда вместо термина нормальная, форма используется термин приведенная форма. Однако, по мнению автора, второй термин является неудачным, так как он не сохраняет преемственности между логикой предикатов и алгеброй логики. И если использовать этот термин, то окажется, что в логике предикатов и в алгебре логики очень похожие понятия называются разными словами, что делает саму логику не логичной. Приведем пример приведения формулы к нормальному виду. Для этого будем использовать равносильные преобразования.

Кванторные операции обусловливают появление новых форм формул (новых относительно алгебры логики). Такой формой является так называемая предваренная нормальная форма (ПНФ).

Определение. Под ПНФ понимается такая форма, в которой кванторные операции либо полностью отсутствуют, либо они предшествуют всем формулам логики предикатов. Иначе говоря, ПНФ имеет вид

где под символами (δx) понимается один из кванторов а формула В кванторов не содержит.

Примерами формул, записанных в ПНФ, являются формулы 1.1). 4). 6); 2.1), 2), 3), 4), 8) из упражнений к подразд. 3.5. А примерами формул. записанных не в ПНФ, являются формулы 1.3), 5); 2.5), 6), 7) из тех же упражнений.

Приведем без доказательства теорему, которая утверждает следующее.

Теорема. Всякая формула логики предикатов может быть приведена к ПНФ.

Пример приведения формулы логики предикатов к ПНФ.

13.Общезначимость и выполнимость формул.

Определение 1.

Формула А логики предикатов называется выполнимой в области М, если существуют значения переменных входящих в эту формулу и отнесенных к области М (иначе – существует модель), при которых формула А принимает истинные значения.

Определение 2.

Формула А логики предикатов называется выполнимой, если существует область, на которой эта формула выполнима.

Определение 3.

Формула А логики предикатов называется тождественно-истинной в области М (выполнимой), если она принимает истинные значения для всех значений переменных, входящих в эту формулу и отнесенных к этой области.

Определение 4.

Формула А логики предикатов называется общезначимой, если она тождественна истинна на всякой области (на любой модели).

Если две равносильные формулы логики предикатов соединить знаком эквиваленции , то полученная формула будет принимать значение И для любого набора переменных в любой области, т.е. будет общезначимой.

Это понятие является обобщением понятия тождественной истинности формулы логики высказываний. Все логические законы, представленный в логике высказываний формулами (1-30) являются общезначимыми формулами логики предикатов и выражают, как и другие общезначимые формулы , законы логики на языке логике предикатов.

Определение 5.

Формула А логики предикатов называется тождественно ложной в области М, если она принимает ложные значения для всех значений переменных, входящих в эту формулу и отнесенных к этой области (иными словами, на данной модели).

Определение 6.

Формула А логики предикатов называется тождественно ложной (невыполнимой), если она тождественно ложна на всякой области (на всякой модели).

Например, формула является тождественно ложной (невыполнимой) формулой логики предикатов.

Из приведенных определений с очевидностью следует:

Если формула А общезначима, то она и выполнима на всякой области (модели)

Если формула А тождественно истинна в области М, то она и выполнима в этой области .

Если формула А тождественно ложна в области М , то она не выполнима в этой области .

Если формула А не выполнима, то она тождественно ложна на всякой области (на всякой модели).

Для того, чтобы формула А логики предикатов была общезначима, необходимо и достаточно, чтобы ее отрицание было не выполнимо.

Для того, чтобы формула А логики предикатов была выполнимой, необходимо и достаточно, чтобы формула была не общезначима.Проблема разрешимости в логике предикатов ставится так же, как и в алгебре логики: существуют ли алгоритмы, позволяющие для любой формулы А логики предикатов установить, к какому типу (классу) она относится, т.е. является ли она общезначимой, выполнимой или тождественно ложной (невыполнимой). Если бы такой алгоритм существовал, то, как и в алгебре высказываний, он сводился бы к критерию тождественной истинности любой формулы логики предикатов. Отметим, что, в отличие от алгебры логики, в логике предикатов не применим метод перебора всех вариантов значений переменных, входящих в формулу, так как таких вариантов может быть бесконечное множество.