
- •Определенный интеграл и его приложения
- •Понятие определенного интеграла
- •Геометрический смысл определенного интеграла
- •Свойства определенного интеграла
- •Вычисления определенного интеграла Формула Ньютона – Лейбница
- •Замена переменной в определенном интеграле
- •Интегрирования по частям в определенном интеграле
- •Вычисление площадей плоских фигур Площадь криволинейной трапеции
- •Объем тела вращения
- •Длина дуги плоской кривой
Определенный интеграл и его приложения
-
Понятие определенного интеграла
Пусть функция
 определена на отрезке
определена на отрезке
 .
Выполним следующие действия.
.
Выполним следующие действия.
-
С помощью точек
 (
( )
разобьем отрезок
)
разобьем отрезок
 на
на
 частичных отрезков
частичных отрезков
 .
.
-
В каждом частичном отрезке
 ,
,
 выберем произвольную точку
выберем произвольную точку
 и вычислим значение функции в этой
точке, т. е.
и вычислим значение функции в этой
точке, т. е.
 ;
; -
Умножим найденное значение
 на длину
на длину
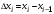 соответствующего
частичного отрезка:
соответствующего
частичного отрезка:
 ;
; -
Составим сумму
 всех таких произведений:
всех таких произведений:
 ,
(1)
,
(1)
Сумма
 называется интегральной суммой
функции
называется интегральной суммой
функции
 на отрезке
на отрезке
 .
Обозначим через
.
Обозначим через
 длину наибольшего частичного отрезка:
длину наибольшего частичного отрезка:

 .
.
-
Найдем предел интегральной суммы, когда
 ,
так что
,
так что .
.

Рис. 1
Если при этом интегральная сумма
 имеет предел I,
который не зависит от способа разбиения
отрезка
имеет предел I,
который не зависит от способа разбиения
отрезка
 на частичные отрезки, ни от выбора точек
на них, то число I
называется определенным интегралом
от функции
на частичные отрезки, ни от выбора точек
на них, то число I
называется определенным интегралом
от функции
 на отрезке
на отрезке
 и обозначается
и обозначается
 .
Таким образом,
.
Таким образом,
 .
(2)
.
(2)
В этом случае функция
 называется интегрируемой
на
называется интегрируемой
на
 .
Числа а
и b
называются соответственно нижним
и верхним пределами интегрирования,
.
Числа а
и b
называются соответственно нижним
и верхним пределами интегрирования,
 – подынтегральной
функцией,
– подынтегральной
функцией,
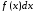 – подынтегральным
выражением,
– подынтегральным
выражением,
 – переменной
интегрирования,
отрезок
– переменной
интегрирования,
отрезок
 называется областью
(отрезком)
интегрирования.
называется областью
(отрезком)
интегрирования.
Теорема 1. Если
функция
 непрерывна на отрезке
непрерывна на отрезке
 ,
то она интегрируема на этом отрезке.
,
то она интегрируема на этом отрезке.
-
Геометрический смысл определенного интеграла
Пусть на отрезке
 задана
непрерывная функция
задана
непрерывная функция
 .
Фигура, ограниченная сверху графиком
функции
.
Фигура, ограниченная сверху графиком
функции
 ,
вертикальными прямыми
,
вертикальными прямыми
 и
и
 сбоку и осью
сбоку и осью
 снизу,
называется криволинейной трапецией.
Рассмотрим разбиение отрезка
снизу,
называется криволинейной трапецией.
Рассмотрим разбиение отрезка
 и соответствующую интегральную сумму
и соответствующую интегральную сумму
 (1). Слагаемые в
(1). Слагаемые в
 (1) равны площадям прямоугольников с
основаниями
(1) равны площадям прямоугольников с
основаниями
 и высотами
и высотами
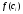 (
( ),
а вся сумма представляет площадь
ступенчатой фигуры, образованной этими
прямоугольниками (Рис. 2). Предел
интегральных сумм (если он существует),
то есть определенный интеграл от
неотрицательной функции численно равен
площади криволинейной трапеции.
),
а вся сумма представляет площадь
ступенчатой фигуры, образованной этими
прямоугольниками (Рис. 2). Предел
интегральных сумм (если он существует),
то есть определенный интеграл от
неотрицательной функции численно равен
площади криволинейной трапеции. 
Рис. 2
Таким образом
 ,
т. е.
,
т. е.
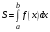 .
.
Таким образом, с геометрической точки зрения определенный интеграл от неотрицательной функции численно равен площади соответствующей криволинейной трапеции.
-
Свойства определенного интеграла
-
Значение определенного интеграла не зависит от обозначения переменной интегрирования:
 .
. -
Определенный интеграл с одинаковыми пределами интегрирования равен нулю
 :
:
 .
Это свойство
следует из определения интеграла.
.
Это свойство
следует из определения интеграла. -
Если
 ,
то, при
перестановке пределов интегрирования
определенный интеграл меняет знак на
противоположный
,
то, при
перестановке пределов интегрирования
определенный интеграл меняет знак на
противоположный
 .
. -
Постоянный множитель можно выносить за знак определенного интеграла:

-
Определенный интеграл от алгебраической суммы двух (и более) функций равен алгебраической сумме определенных интегралов от этих функций:
 .
.
-
Если функция
 интегрируема на
интегрируема на
 и
и
 ,
то
,
то
 (аддитивность
определенного интеграла).
(аддитивность
определенного интеграла). -
Если

 ,
то
,
то
 .
. -
Если интегрируемые функции
 и
и
 удовлетворяют неравенству
удовлетворяют неравенству

 ,
то
,
то
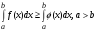 (определенность
определенного интеграла).
(определенность
определенного интеграла). -
Если m и М – соответственно наименьшее и наибольшее значения функции
 непрерывной на отрезке
непрерывной на отрезке
 ,
то
,
то
 .
. -
(Теорема о среднем). Если функция
 непрерывна на отрезке
непрерывна на отрезке
 ,
то на этом отрезке существует точка
,
то на этом отрезке существует точка
 ,
такая, что
,
такая, что
 .
.
