8. Непрерывные функции. Определение непрерывности с помощью приращений.

Н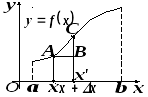а рисунке изображен график функции . Зададим точку . Близкая ей точка , где - приращение . Разность

называется приращением функции в точке , соответствующим приращению . На рисунке , .

Будем стремить к нулю. Тогда для рассматриваемой функции и будет стремиться к нулю

Рассмотрим теперь график другой функции . Придадим теперь приращение и определим соответствующее приращение функции

Если мы будем стремить к нулю, то теперь уже нельзя сказать, что стремится к нулю.

Теперь можно дать определение.

Функцию , заданную на отрезке , называют непрерывной в точке этого отрезка, если приращение ее в этой точке, соответствующее приращению , стремится к нулю при любом способе стремления к нулю.

Это свойство непрерывности в точке записывают в виде

В противном случае функция называется разрывной.

Функция непрерывная в любой точке отрезка (интервала), называется непрерывной на этом отрезке (интервале).

Функция называется непрерывной в точке , если она определена в некоторой окрестности этой точки, в том числе и в самой точке , и если ее приращение в этой точке, соответствующее приращению аргумента , стремится к нулю при

Либо ; ;

.

Пример. Функция непрерывна для любого . В самом деле.

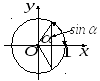
Но для любого имеет место неравенство . Если , то это следует из рисунка (длина дуги больше стягивающей ее хорды). Отсюда следует

Но тогда, очевидно, . Что и требовалось доказать.

Если функции и непрерывны в точке , то непрерывны также в этой точке их сумма, разность, произведение и частное (при ).

Пример. Функция непрерывна. Она является композицией двух непрерывных функций: , и .

Точки разрыва и их классификация.

Пусть функция – имеет предел в точке слева (справа). Если:

а сама функция в точке не определена, то эта точка называется устранимой точкой разрыва.

Если функция такова, что существуют пределы в точке , но верхнее равенство не выполняется, то функция в точке имеет разрыв первого рода.

Если у функции не существует правого предела или левого предела в точке , или не существует как правого, так и левого предела, или же эти пределы бесконечны, то функция в этой точке имеет разрыв второго рода.

Например, функция . Точка - точка разрыва второго рода, .

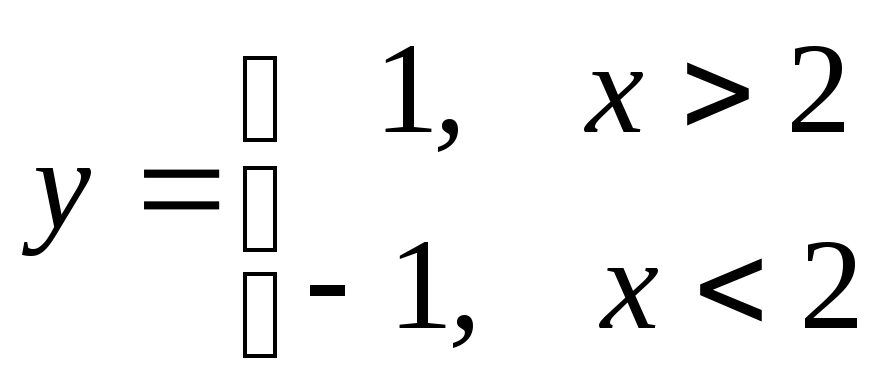Теорема 4. Если не убывает на отрезке , то существуют пределы и .

Следствие. Если не убывает на отрезке , то в любой точке существует правый предел и в любой точке существует левый предел .

Теоремы о непрерывных функциях

Функция называется непрерывной на отрезке , если она непрерывна во всех точках интервала , непрерывна справа в точке и непрерывна слева в точке .

Т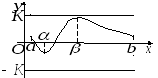еорема 5. Если функция непрерывна на отрезке , то она ограничена на нем, т.е. существует константа такая, что выполняется неравенство

На рисунке изображен график непрерывной функции на отрезке . Очевидно, что существует такое число , что график находится ниже прямой , но выше прямой .

Теорема 6 (Вейерштрассе). Если функция непрерывна на , то существует ее минимум и максимум на , т.е. существуют точки такие, что для всех . См. рис.

Теорема 7. Если функция непрерывна на отрезке и числа и не равны нулю и имеют разные знаки, то на интервале имеется п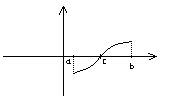о крайней мере одна точка такая, что .

Следствие 1. Если функция непрерывна на , , , и произвольное число, находящееся между числами и , то на интервале найдется по крайней мере одна точка такая, что .

Следствие 2. Непрерывная на отрезке функция принимает все промежуточные значения между ее наименьшим и наибольшим значениями.