«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра «Теория механизмов и машин»

Пресс чеканочный.

Курсовая работа

Студент группы: 3066/2

Никулин Василий

Проверил:

Терешин В.А.

Санкт-Петербург

2011

Содержание:

Техническое задание.
Структурный анализ.
План-положения.
Кинематический анализ:
Аналитический метод.
План скоростей.
План ускорений.
Силовой расчет.

1. Техническое задание

Цель: рассчитать скорости и ускорения отдельных звеньев, сделать силовой расчет, показать это графически.

Рисунок 1.1 – Схема механизма

Дано: OA=0,1 м

AB=0,35 м

LB=0,24 м

OL=0,32 м;

LD=0.4 м

CK=0.3 м

a=0,28 м

ω=6 c ^-1

D_П=0.2 м

Р=6 Атм

2. Структурный анализ механизма

Исследуемый механизм, кинематическая схема, которого приведена на рисунке: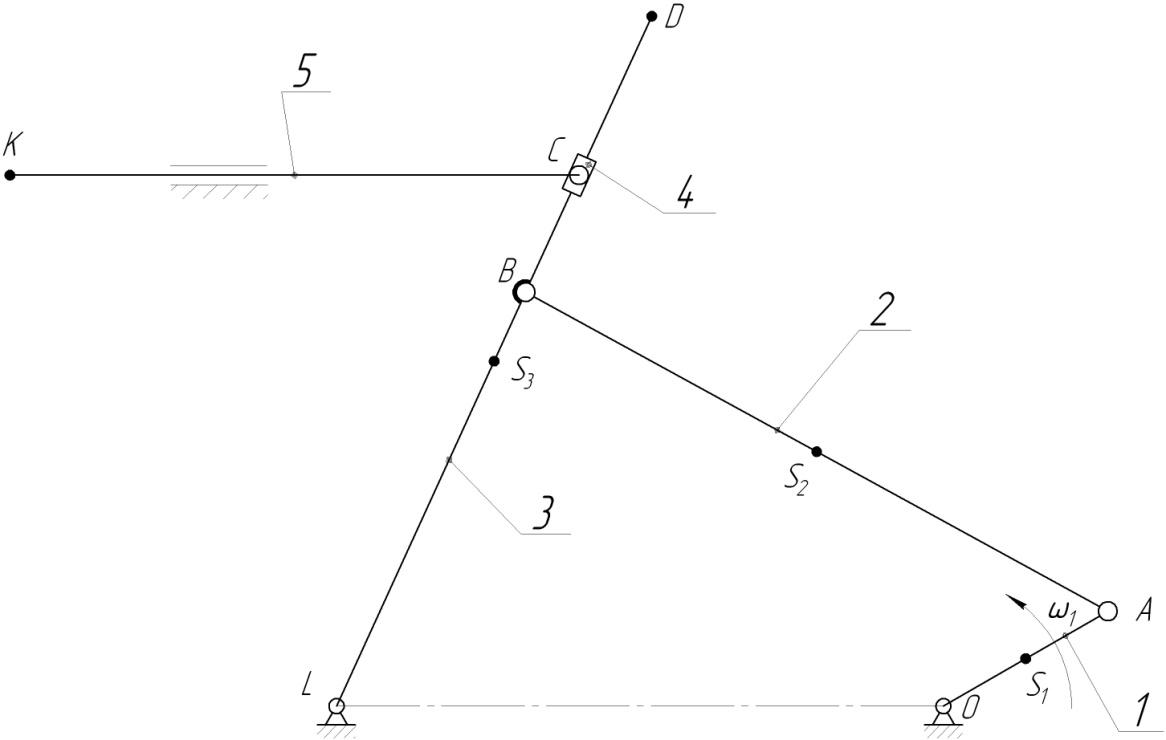

Рисунок 2. 1 – Кинематическая схема механизма

Определяем степень подвижности механизма по формуле:

,

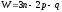где, р – число кинематических пар;

n – число подвижных звеньев

Так как W=1 , то у механизма одно входное звено.

0-стойка;

1-кривошип;

2-шатун;

3-кулиса;

4-камень кулисы;

5-ползун.

О(0-1)-вращающаяся кинематическая пара;

А(1-2) - вращающаяся кинематическая пара;

B(2-3) - вращающаяся кинематическая пара;

L(3-0) - вращающаяся кинематическая пара;

C₃(3-4) - вращающаяся кинематическая пара;

C₅(5-4) - поступательная кинематическая пара.

Механизм образован присоединением к неподвижной оси 0 кривошипа, который образует с ним вращательную пару (т.О). Кривошип 1 совершает вращательное движение вокруг неподвижной оси. Шатун 2 совершает сложное плоскопараллельное движение и присоединен к кривошипу 1(т.А).

Кулиса 3 присоединена к шатуну 2, образуя с ним вращательную КП (т.В). Кулиса 3 осуществляет неполное вращательное движение вокруг неподвижной оси. К кулисе 3 присоединяется камень кулисы 4, образовывая вращательную КП (т.С). Камень кулисы 4 присоединен к ползуну 5 и к кулисе 3. Ползун 5 осуществляет поступательное движение вдоль направляющей, образуя с ней поступательную кинематическую пару (т.К).

Разбиваем механизм на группы Асура:

Рисунок 2.2 – Структурная группа 4-5

Рисунок 2.3 – Структурная группа 2-3

W=3n-2p=3*2-2*3=0

Рисунок 2.4 Начальный механизм.

W=3n-2p=3*1-2*1=1

Рисунок 2.5 Структурные группы и граф механизма.

3. Построение плана положений механизма

4) Кинематический анализ.

4.1) Аналитический расчет скоростей и ускорений

Для определения скоростей и ускорений аналитическим способом воспользуемся методом замкнутых векторных контуров.

Рассмотрим первый векторный контур (рисунок 2.5).

Рисунок 4.1. – Первый векторный контур

Рассмотрим векторний контур ОАBL. Запишем условия замкнутости контура:

(1)

Уравнение (1) проектируем на оси координат :

(2)

Система (2) есть системой с неизвестными углами φ₂ и φ₃. Для решения системы контур ОАBL разбиваем на два ОАL и АBL.

Рассмотрим контур ОАL и запишем условия замкнутости контура:

(3)

Уравнения (3) проектируем на оси координат:

(4)

Из системы (4) находим и

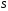
Рассмотрим контур АBL и определим углы φ_s3 и φ_s3 по теореме косинусов.

Теперь мы можем определить углы φ₂ и φ₃.

Для определения аналогов угловых скоростей ω₂ и ω₃ звеньев 2 и 3 дифференцируем уравнения (2) по обобщенной координате φ₁

(5)

Имея ввиду, что есть аналог угловой скорости ω₂ звена 2 и есть аналог угловой скорости ω₃ звена 3 получаем

(6)

Из углов, входящих в первое уравнение (6), вычитаем общий угол φ₂, что соответствует повороту осей координат xAy на общий угол φ₂. Имеем

откуда получаем выражения для аналога u₃₁ и угловой скорости ω₃

После аналогичного преобразования того же уравнения поворотом осей координат на угол φ₃ получаем выражение для аналога u₂₁ и угловой скорости ω₂

Для определения угловых ускорений ε₂ и ε₃ звеньев 2 и 3 дифференцируем по обобщенной координате φ₁ уравнение (6) что приводит к уравнению

(7)

где, и - аналоги угловых ускорений. Величины аналогов можно определить, если выполнить преобразования координат последовательным поворотом осей координат на углы φ₂ и φ₃. Имеем

Таким образом, находим истинные угловые скорости и ускорения звеньев 2 и 3 равны

Рассмотрим второй векторный контур (рисунок 4.2)

Рисунок 4.2 – Второй векторный контур

Запишем векторное уравнение контура

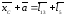(8)

Уравнение (8) проектируем на оси координат

(9)

Из системы (9) находим

Для определения аналогов скоростей и ускорений систему (9) продифференцируем по обобщенной координате φ₁

(10)

Для определения аналога ускорений уравнения (10) продифференцируем по обобщенной координате φ₁

Таким образом, находим истинные скорости и ускорения звеньев 3 4 5