5)Свойства определителя n-го порядка

Свойство 1. При замене строк столбцами (транспонировании)

значение определителя не изменится, т.е.

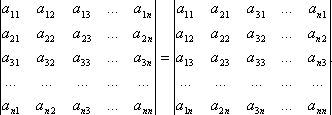Свойство 2. Если хотя бы один ряд

(строка или столбец) состоит из нулей, то определитель равен нулю. Доказательство очевидно.

В самом деле, тогда в каждом члене определителя один из множителей будет нуль.

Свойство 3. Если в определителе поменять местами два соседних параллельных ряда

(строки или столбцы), то определитель поменяет знак на противоположный, т.е.

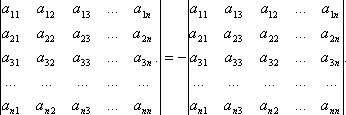Свойство 4. Если в определителе имеются

два одинаковых параллельных ряда, то определитель равен нулю:

Свойство 5. Если в определителе два параллельных

ряда пропорциональны, то определитель равен нулю:

Свойство 6. Если все элементы определителя, стоящие в

одном ряду, умножить на одно и то же число, то значение определителя изменится в это число раз:

Следствие. Общий множитель, содержащийся во всех элементах

одного ряда, можно вынести за знак определителя, например:

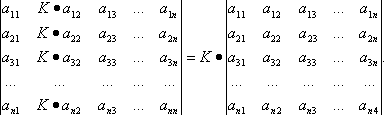Свойство 7. Если в определителе все элементы

одного ряда представлены в виде суммы двух слагаемых, то он равен сумме двух определителей:

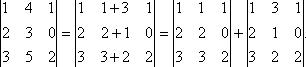Свойство 8. Если к элементам какого-либо ряда

прибавить произведение соответствующих элементов параллельного ряда на постоянный множитель, то

значение определителя не изменится:

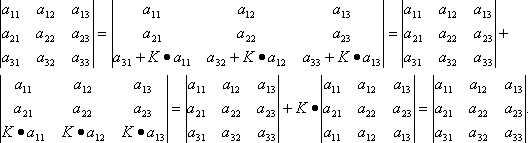Свойство 9. Если к

элементам i-го ряда прибавить линейную комбинацию соответствующих элементов нескольких параллельных

рядов, то значение определителя не изменится:

Справедливость этого равенства вытекает из свойства 8.

6)Системы линейных уравнений: основные понятия

Определение. Система линейных уравнений — это объединение из n линейных уравнений,

каждое из которых содержит k переменных. Записывается это так:

Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают,

что число уравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и 

бывает, однако для высшей алгебры это, вообще говоря, неверно.Определение. Решение системы

уравнений — это последовательность чисел (k₁, k₂, ..., k_n), которая является решением каждого уравнения

системы, т.е. при подстановке в это уравнение вместо переменных x₁, x₂, ..., x_n дает верное числовое равенство.

Соответственно, решить систему уравнений — значит найти множество всех ее решений или доказать, что это 

множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:

Система несовместна, т.е. множество всех решений пусто. Достаточно редкий случай, который легко

обнаруживается независимо от того, каким методом решать систему.

Система совместна и определена, т.е. имеет ровно одно решение. Классический вариант, хорошо

известный еще со школьной скамьи.

Система совместна и не определена, т.е. имеет бесконечно много решений. Это самый жесткий

вариант. Недостаточно указать, что «система имеет бесконечное множество решений» — надо описать,

как устроено это множество.

Определение. Переменная x_i называется разрешенной, если она входит только в одно уравнение системы, причем с

 коэффициентом 1. Другими словами, в остальных уравнениях коэффициент при переменной x_i должен быть равен нулю.

Если в каждом уравнении выбрать по одной разрешенной переменной, получим набор разрешенных переменных для всей

системы уравнений. Сама система, записанная в таком виде, тоже будет называться разрешенной. Вообще говоря, одну и 

ту же исходную систему можно свести к разным разрешенным, однако сейчас нас это не волнует. Вот примеры разрешенных систем:

Обе системы являются разрешенными относительно переменных x₁, x₃ и x₄. Впрочем, с тем же

успехом можно утверждать, что вторая система — разрешенная относительно x₁, x₃ и x₅. Достаточно переписать самое последнее

уравнение в виде x₅ = x₄.Теперь рассмотрим более общий случай. Пусть всего у нас k переменных, из которых r являются разрешенными.

Тогда возможны два случая:

Число разрешенных переменных r равно общему числу переменных k: r = k. Получаем систему

из k уравнений, в которых r = k разрешенных переменных. Такая система является совместной и определенной,

т.к. x₁ = b₁, x₂ = b₂, ..., x_k = b_k;

Число разрешенных переменных r меньше общего числа переменных k: r < k. Остальные (k − r) переменных называются

свободными — они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.

Так, в приведенных выше системах переменные x₂, x₅, x₆ (для первой системы) и x₂, x₅ (для второй) являются свободными. Случай,

когда есть свободные переменные, лучше сформулировать в виде теоремы:

Теорема. Если в системе из n уравнений переменные x₁, x₂, ..., x_r — разрешенные, а x_r + 1, x_r + 2, ..., x_k — свободные, то: Если задать значения

свободным переменным (x_r + 1 = t_r + 1, x_r + 2 = t_r + 2, ..., x_k = t_k), а затем найти значения x₁, x₂, ..., x_r, получим одно из решений.

Если в двух решениях значения свободных переменных совпадают, то значения разрешенных переменных тоже совпадают,

т.е. решения равны.В чем смысл этой теоремы? Чтобы получить все решения разрешенной системы уравнений, достаточно выделить

свободные переменные. Затем, присваивая свободным переменным разные значения, будем получать готовые решения. Вот и 

все — таким образом можно получить все решения системы. Других решений не существует.Вывод: разрешенная система уравнений

всегда совместна. Если число уравнений в разрешенной системе равно числу переменных, система будет определенной, если

— неопределенной.

---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

7) Метод Крамера (правило Крамера) — способ решения квадратных систем линейных

алгебраических уравнений с ненулевым определителем основной матрицы (причём для

таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера

(1704–1752), придумавшего метод.[править]Описание методаДля системы n линейных уравнений

с n неизвестными (над произвольным полем)

с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде

(i-ый столбец матрицы системы заменяется столбцом свободных членов). В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n

справедливо равенство: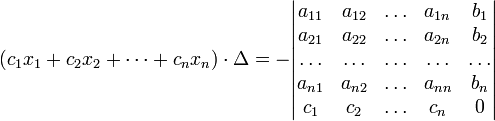В этой

форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно

даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель

системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что

либо наборы b₁,b₂,...,b_n и x₁,x₂,...,x_n, либо набор c₁,c₂,...,c_n состоят не из элементов кольца коэффициентов

системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется,

например, при доказательстве формулы для определителя Грама и Леммы Накаямы.