Теория рекурсивных функций

С каждый алгоритмом однозначно связана функция, которую он вычисляет. Возникает естественный вопрос, для всякой ли функции существует вычисляющий её алгоритм. Учитывая сформулированный тезис Тьюринга, данный вопрос трансформируется в следующий. Для всякой ли функции можно указать вычисляющую её машину Тьюринга? Если нет, то для каких функций существует вычисляющий их алгоритм (машина Тьюринга), как описать такие, как говорят, алгоритмически или эффективно вычислимые функции?

Исследование этих вопросов привело к созданию в 1930-ч годах теории рекурсивных функций. Сначала были выбраны простейшие функции, эффективная вычисляемость которых была очевидна. Затем сформулированы некоторые правила (операторы), на основе которых можно строить новые функции из уже имеющихся. Тогда требуемым классом функций будет совокупность всех функций, получающихся из простейших с помощью выбранных операторов. Наша цель будет состоять в тот, чтобы доказать, что этот класс функций совпадёт с классом функций, вычислимых с помощью машин Тьюринга.

Рекурсия - метод определения функции через её предыдущие и ранее определенные значения, а так же способ организации вычислений, при котором функция вызывает сама себя с другим аргументом.

Функция f называется вычислимой, если существует алгоритм её вычисления с произвольными переменными.

Понятие рекурсивной функции введено из следующих соображений. Некоторые функции объявляются первичными (базовыми). Первичную функцию нельзя заменить вычислением более простых функций. Из этих первичных функций строится с помощью определенных операций все множество известных нам вычислимых функций. Таких первичных функций над целыми положительными числами всего три.

А). Функция константа

Б) Функция непосредственного следования

В) Тождественная функция

Для построения более сложных функций из первичных используют следующие операторы:

• Операция подстановки. Эта операция заключается в том, что вместо каких-то переменных функции подставляют другие функции от тех же или иных переменных.

Пример. Пусть и . Тогда подставив вместо переменной х функцию g(у), получим новую функцию:

• Операция примитивной рекурсии. Эту операцию можно представить следующим образом

Пример 1. Пусть - известная вычислимая функция, т.е. известен алгоритм вычисления этой функции для произвольного х. Определим новую функцию f(x) следующим образом:

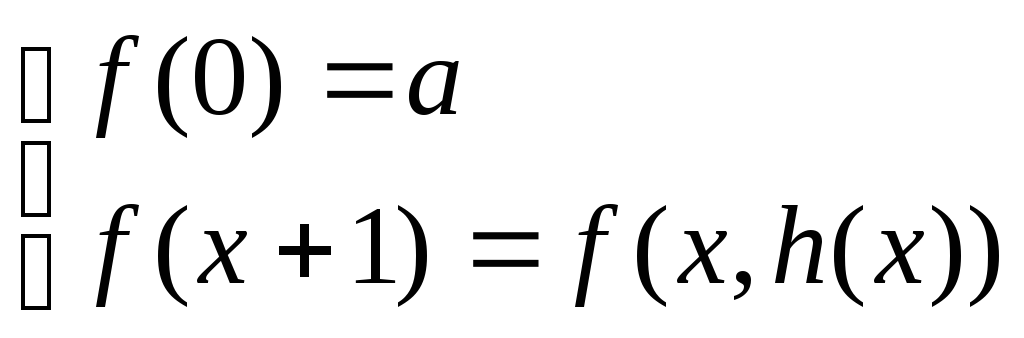
Это и есть определение функции с помощью операции примитивной рекурсии. Например, пусть

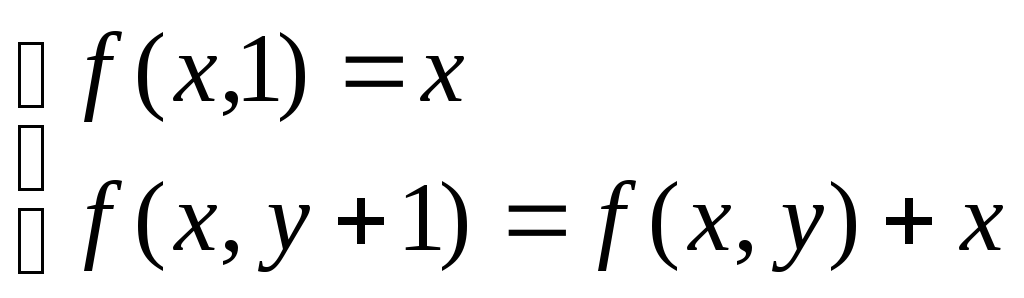
Это есть определение целочисленного умножения. Так f(3,3)=f(3,2)+3=f(3,1)+3+3=3+3+3=9.

Пример 2. 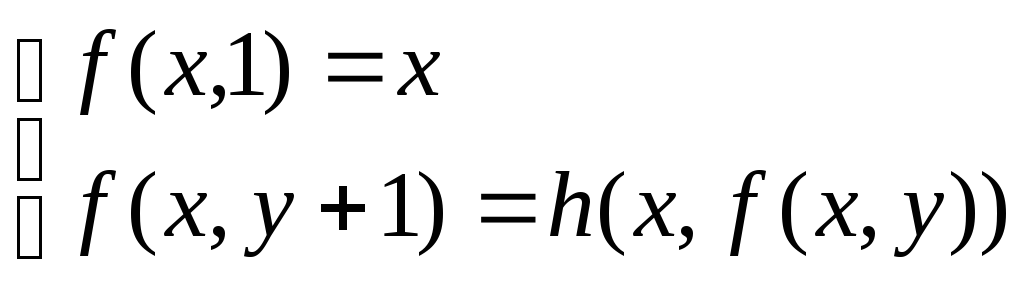и

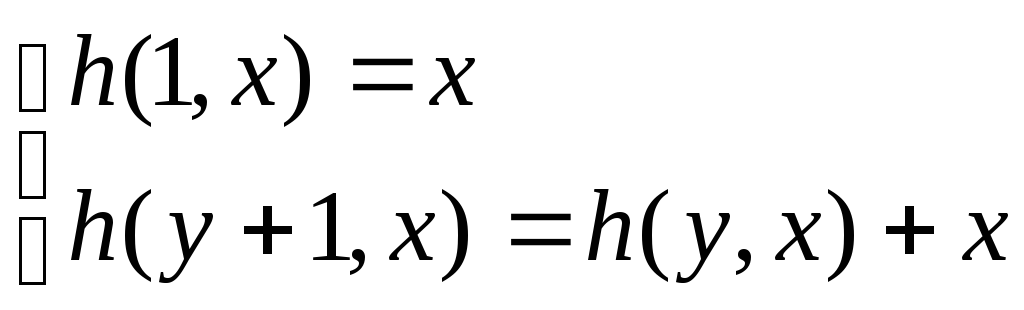
Это определение позволяет находить значение . В самом деле, рассмотрим следующий пример вычисления 3² .

f(3,1+1)=h(3,f(3,1))=h(3,3)=h(2+1,3)=h(2,3)+3=h(1+1,3)+3=h(1,3)+3+3=3+3+3=9

Функция, определяемая из простейших с помощью операций подстановки и/или примитивной рекурсии, называется примитивно рекурсивной.

Имеется еще одна операция для построения рекурсивных функций. Правда, эта операция не всегда дает результат или, как говорят, не является полностью определенной (тотальной). Эта операция называется операцией минимизации (взятия минимального корня). Ее определение таково.

• 

Эту операции можно для простоты обозначить как _y f(x,y).

Пример 3. Пусть . Тогда _y f(3,y)=2.

Функция, определяемая из простейших с помощью операций подстановки примитивной рекурсии и минимизации, называется частично рекурсивной.

Тезис Черча. Класс всех частично вычислимых функций над положительными целыми числами совпадает с классом всех частично рекурсивных функций.

Иными словами, каждая арифметическая функция, для которой имеется машина Тьюринга, является одновременно и рекурсивной, и наоборот – если функция является частично-рекурсивной, то она одновременно и вычислима.

Общерекурсивные функция – функция всюду определена, частично рекурсивная функция.