2. Симплекс метод решения задач линейного программирования

В основе симплексного метода решения ЗЛП лежит, с некоторыми дополнениями метод ОЖИ, построенных на последовательном применении симплексных преобразований системы уравнений.

К левой части неравенств добавляется положительная величина y_i > 0 (i = 1, 2, 3…), называемая выравнивающей или базисной переменной, преобразующая их в уравнения.

Порядок выполнения симплексного преобразования:

1. выбираем разрешающий столбец, по наименьшему отрицательному элементу в z-строке;

2. выбираем разрешающую строку, по наименьшему из положительных отношений элементов правой части систему на соответствующие элементы разрешающего столбца;

На пересечении разрешающего столбца и разрешающей строки располагается разрешающий элемент.

3. элементы разрешающей строки делятся на разрешающий элемент, а элементы разрешающего столбца обращаются в 0;

4. все элементы остальных строк определяются по формуле:

НЭ = СЭ – (СЭР_стр ∙ СЭР_стлб)/РЭ,

где НЭ – новый элемент;

СЭ – старый элемент;

СЭР_стр – старый элемент разрешающей строки;

СЭР_стлб – старый элемент разрешающего столбца;

РЭ – разрешающий элемент.

Процесс последовательных симплексных преобразований является процессов решения, при этом:

1. если в z-строке найдется, хоть один отрицательный элемент и:

• в разрешающем столбце найдется один положительный элемент, то решение можно улучшить;

• в разрешающем столбце не будет положительных элементов, то z неограниченно возрастает;

2. если все элементы в z-строке не отрицательные, то достигнуто оптимальное решение.

Задача №2.

Предприятие производит 3 вида изделий А, В и С располагая ограниченным объемом ресурсов чугуна и стали (1400 и 1800 кг соответственно) и оборудованием (800 ст./час).

На производство изделия А требуется 2 кг чугуна, 4 кг стали и 2 ст./час оборудования; изделия В – 4 кг чугуна, 1 кг стали и 1 ст./час оборудования, а изделия С – 3 кг чугуна, 1,5 кг стали и 1,5 ст./час оборудования.

Стоимость изделия А – 45$; изделия В - 50$; изделия С - 60$.

Необходимо определить сколько изделий А, В и С должно производить предприятие, чтобы достичь максимальной прибыли.

Решение

Для решения задачи необходимо разработать модель. Пусть x₁ – количество изделий А, x₂ – количество изделий В, x₃ – количество изделий С. Тогда по условию задачи среди множества неотрицательных решений имеем систему неравенств:

2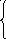x₁ + 4x₂ + 3x₃ = 1400;

4x₁ + x₂ + 1½ x₃ = 1800;

2x₁ + x₂ + 1½ x₃ = 800.

Необходимо найти решение, для которого целевая функция стремится к наибольшему значению: z = 45x₁ + 50x₂ + 60x₃ → max.

Вид ресурсов	Объем ресурсов	Затраты на 1 изделие, кг
		А	В	С
Чугун	1400	2	4	3
Сталь	1800	4	1	1 ½
Оборудование	800	2	1	1 ½
Прибыль, $		45	50	60

Добавив к левой части неравенств положительную величину y_i > 0 (i = 1, 2, 3…), называемую выравнивающей или базисной переменной, превратим их в уравнения:

2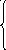x₁ + 4x₂ + 3x₃ + y₁ + 0 + 0 = 1400;

4x₁ + x₂ + 1½ x₃ + 0 + y₂ + 0 = 1800;

2x₁ + x₂ + 1½ x₃ + 0 + 0 + y₃ = 800;

-45x₁ – 50x₂ – 60x₃ + 0 + 0 + 0 + z = 0.

Выбираем разрешающий столбец, соответствующий наименьшему отрицательному значению в z-строке, так как теоретически установлено, что при этом можно ожидать большое увеличение функции z.

Элементы правой части системы делим на элементы разрешающего столбца и выбираем наименьшее положительное отношение, соответствующее разрешающей строке.

На пересечении выделенных элементов строки и столбца стоит разрешающее число.

Элементы разрешающей строки делим на разрешающий элемент, элементы разрешающего столбца обращаются в 0. Все элементы остальных строк определяем по формуле нового элемента (НЭ).

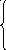
x₁ + x₂ + x₃ + y₁ + 0 + 0 = 466;

3x₁ – x₂ + 0 – ½ y₁+ y₂ + 0 = 1100;

x₁ – x₂ + 0 – ½ y₁ + 0 + y₃ = 100;

-5x₁ + 30x₂ + 0 + 20y₁ + 0 + 0 + z = 28000.

НЭ₂₁ = 4 – (2 ∙ 1,5)/3 = 3;

НЭ₂₂ = 1 – (4 ∙ 1,5)/3 = -1;

НЭ₂₄ = 0 – (1 ∙ 1,5)/3 = - ½;

НЭ₂₅ = 1 – (0 ∙ 1,5)/3 = 1;

НЭ₂₆ = 0 – (0 ∙ 1,5)/3 = 0;

НЭ₂₇ = 1800 – (1400 ∙ 1,5)/3 = 1100;

НЭ₃₁ = 2 – (2 ∙ 1,5)/3 = 1;

НЭ₃₂ = 1 – (4 ∙ 1,5)/3 = -1;

НЭ₃₄ = 0 – (1 ∙ 1,5)/3 = - ½;

НЭ₃₅ = 0 – (0 ∙ 1,5)/3 = 0;

НЭ₃₆ = 1 – (0 ∙ 1,5)/3 = 1;

НЭ₃₇ = 800 – (1400 ∙ 1,5)/3 = 100;

НЭ₄₁ = -45 – (2 ∙ (-60))/3 = -5;

НЭ₄₂ = -50 – (4 ∙ (-60))/3 = 30;

НЭ₄₄ = 0 – (2 ∙ (-60))/3 = 20;

НЭ₄₅ = 0 – (0 ∙ (-60))/3 = 0;

НЭ₄₆ = 0 – (0 ∙ (-60))/3 = 0;

НЭ₄₇ = 0 – (1400 ∙ (-60))/3 = 28000.

Так как в z-строке присутствует отрицательный элемент, то решение можно улучшить. Для этого в полученной матрице находим разрешающий столбец, разрешающую строку и разрешающий элемент соответственно. Элементы разрешающей строки делим на разрешающий элемент, элементы разрешающего столбца обращаются в 0. Все элементы остальных строк определяем по формуле нового элемента (НЭ).

0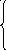 + 2x₂ + x₃ + y₁ + 0 + 0 = 400;

0 + 2x₂ + 0 + y₁+ y₂ – 3y₃= 800;

x₁ – x₂ + 0 – ½ y₁ + 0 + y₃ = 100;

0 + 25x₂ + 0 + 17 ½ y₁ + 0 + 5y₃ + z = 28500.

НЭ₁₂ = – ((-1) ∙ )/1 = 2;

НЭ₁₃ = 1 – (0 ∙ )/1 = 1;

НЭ₁₄ = – (- ½ ∙ )/1 = ;

НЭ₁₅ = 0 – (0 ∙ )/1 = 0;

НЭ₁₆ = 0 – (0 ∙ )/1 = 0;

НЭ₁₇ = 466 – (100 ∙ )/1 = 400;

НЭ₂₂ = -1 – (3 ∙ (-1))/1 = 2;

НЭ₂₃ = 0 – (0 ∙ 3)/1 = 0;

НЭ₂₄ = - ½ – ((- ½) ∙ 3)/1 = 1;

НЭ₂₅ = 1 – (0 ∙ 3)/1 = 1;

НЭ₂₆ = 0 – (1 ∙ 3)/1 = -3;

НЭ₂₇ = 1100 – (100 ∙ 3)/1 = 800;

НЭ₄₂ = 30 – ((-1) ∙ (-5))/1 = 25;

НЭ₄₃ = 0 – (0 ∙ (-5))/1 = 0;

НЭ₄₄ = 20 – ((- ½) ∙ (-5))/1 = 17 ½;

НЭ₄₅ = 0 – (0 ∙ (-5))/1 = 0;

НЭ₄₆ = 0 – (1 ∙ (-5))/1 = 5;

НЭ₄₇ = 28000 – (100 ∙ (-5))/1 = 28500.

Все элементы в z-строке неотрицательны, значит достигнуто оптимальное решение. Для получения максимальной прибыли предприятию необходимо производить 100 изделий вида А и 400 изделий вида С.

Найдем значение целевой функции: z = 400 ∙ 60 + 100 ∙ 45 = 24000 + 4500 = 28500.