Конспект лекций

По предмету

Системное программное обеспечение

Казань, 2009

Лекция 1.

Введение. Предмет "Системное программное обеспечение", основные поня­тия.

Операционные системы и среды

В англоязычной технической литературе термин System Software (системное программное обеспечение) означает программы и комплексы программ, являющиеся общими для всех, кто совместно использует технические средства компьютера и применяемые как для автоматизации разработки (создания) новых программ так и для организации выполнения программ существующих. С этих позицию системное программное обеспечение может быть разделено на следующие пять групп:

1. Операционные системы.

2. Системы управления файлами.

1. Интерфейсные оболочки для взаимодействия пользователя с ОС и программ ные среды.

3. Системы программирования.

4. Утилиты.

Рассмотрим вкратце эти группы системных программ.

1. Под операционной системой (ОС) обычно понимают комплекс управляющих и обрабатывающих программ, который, с одной стороны, выступает как интерфейс между аппаратурой компьютера и пользователем его задачам! а с другой — предназначен для наиболее эффективного использования ресурсов вычислительной системы и организации надежных вычислений. Любо: из компонентов прикладного программного обеспечения обязательно рабе тает под управлением ОС. На рис. 1 изображена обобщенная структура прс граммного обеспечения вычислительной системы. Видно, что ни один и компонентов программного обеспечения, за исключением самой ОС, не имеет непосредственного доступа к аппаратуре компьютера. Даже пользовател аимодействуют со своими программами через интерфейс ОС. Любые их шанды, прежде чем попасть в прикладную программу, сначала проходят!

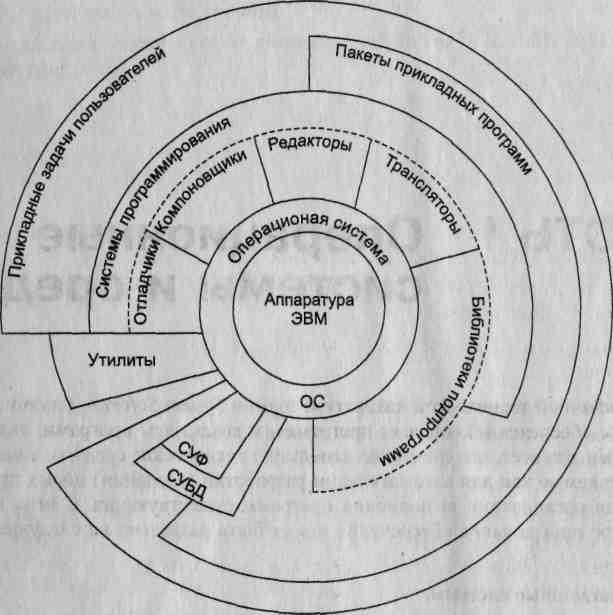Рис.1. Обобщенная структура программного обеспечения вычислительной системы

Основными функциями, которые выполняет ОС, являются следующие:

- прием от пользователя (или от оператора системы) заданий или команд, сформулированных на соответствующем языке — в виде директив (ко­манд) оператора или в виде указаний (своеобразных команд) с помощью соответствующего манипулятора (например, с помощью мыши), — и их обработка;

- прием и исполнение программных запросов на запуск, приостановку, оста­новку других программ;

- загрузка в оперативную память подлежащих исполнению программ; Э инициация программы (передача ей управления, в результате чего процес­сор исполняет программу); идентификация всех программ и данных;

- обеспечение работы систем управлений файлами (СУФ) и/или систем управления базами данных (СУБД), что позволяет резко увеличить эф­фективность всего программного обеспечения;

- обеспечение режима мультипрограммирования, то есть выполнение двух или более программ на одном процессоре, создающее видимость их одно­временного исполнения;

- обеспечение функций по организации и управлению всеми операциями ввода/вывода;

- удовлетворение жестким ограничениям на время ответа в режиме реаль­ного времени (характерно для соответствующих ОС);

- распределение памяти, а в большинстве современных систем и организа­ция виртуальной памяти;

О планирование и диспетчеризация задач в соответствии с заданными стра­тегией и дисциплинами обслуживания;

- организация механизмов обмена сообщениями и данными между выпол­няющимися программами;

- защита одной программы от влияния другой; обеспечение сохранности данных;

- предоставление услуг на случай частичного сбоя системы;

- обеспечение работы систем программирования, с помощью которых поль­зователи готовят свои программы.

2. Назначение системы управления файлами — организация более удобного доступа к данным, организованным как файлы. Именно благодаря системе управления файлами вместо низкоуровневого доступа к данным с указанием конкретных физических адресов нужной нам записи используется логиче­ский доступ с указанием имени файла и записи в нем. Как правило, все совре­менные ОС имеют соответствующие системы управления файлами. Однако выделение этого вида системного программного обеспечения в отдельную ка­тегорию представляется целесообразным, поскольку ряд ОС позволяет рабо­тать с несколькими файловыми системами (либо с одной из нескольких, либо сразу с несколькими одновременно). В этом случае говорят о монтируемых файловых системах (дополнительную систему управления файлами можно установить), и в этом смысле они самостоятельны. Более того, можно назвать примеры простейших ОС, которые могут работать и без файловых систем, а значит, им необязательно иметь систему управления файлами, либо они мо­гут работать с одной из выбранных файловых систем. Надо понимать, что любая система управления с файлами не существует сама по себе — она разработана для работы в конкретной ОС и с конкретной файловой систе­мой. Можно сказать, что всем известная файловая система FAT (file allocation table)¹ имеет множество реализаций как система управления файлами, напри­мер FAT-16 для самой MS-DOS, super-FAT для OS/2, FAT для Windows NT

Здесь и далее без указания на источник заимствования приводятся английские эквива­ленты слов и словосочетаний.

т. д. Другими словами, для работы с файлами, организованными в соответ-вии с некоторой файловой системой, для каждой ОС должна быть разра-1тана соответствующая система управления файлами; и эта система управ-ния файлами будет работать только в той ОС, для которой она и создана.

гя удобства взаимодействия с ОС могут использоваться дополнительные гтерфейсные оболочки. Их основное назначение — либо расширить возможности по управлению ОС, либо изменить встроенные в систему возможности, в качестве классических примеров интерфейсных оболочек и соответствующих операционных сред выполнения программ можно назвать различные варианты графического интерфейса X Window в системах семейства UNIX апример, К Desktop Environment в Linux), PM Shell или Object Desktop OS/2 с графическим интерфейсом Presentation Manager; наконец, можно :азать разнообразные варианты интерфейсов для семейства ОС Windows Алании Microsoft, которые заменяют Explorer и могут напоминать либо NTX с его графическим интерфейсом, либо OS/2, либо MAC OS. Следует метить, что о семействе ОС компании Microsoft с общим интерфейсом, реа-[зуемым программными модулями с названием Explorer (в файле system.ini, •торый находится в каталоге Windows, имеется строка SHELL=EXPLORER.EXE), е же можно сказать, что заменяемой в этих системах является только ин-рфейсная оболочка, в то время как сама операционная среда остается неиз-;нной; она интегрирована в ОС. Другими словами, операционная среда феделяется программными интерфейсами, то есть API (application program terface). Интерфейс прикладного программирования (API) включает в себя управление процессами, памятью и вводом/выводом.

ад операционных систем могут организовывать выполнение программ, соз-нных для других ОС. Например, в OS/2 можно выполнять как программы, зданные для самой OS/2, так и программы, предназначенные для выполнения в среде MS-DOS и Windows 3.x. Соответствующая операционная среда танизуется в операционной системе в рамках отдельной виртуальной ма-ины. Аналогично, в системе Linux можно создать условия для выполнения некоторых программ, написанных для Windows 95/98. Определенными воз-шностями исполнения программ, созданных для иной операционной среды, ■ладает и Windows NT. Эта система позволяет выполнять некоторые про-аммы, созданные для MS-DOS, OS/2 1.x, Windows 3.x. Правда, в своем по-еднем семействе ОС Windows XP разработчики решили отказаться от 'Ддержки возможности выполнения DOS-программ.

аконец, к этому классу системного программного обеспечения следует отне-и и эмуляторы, позволяющие смоделировать в одной операционной сис-ме какую-либо другую машину или операционную систему. Так, известна схема эмуляции WMWARE, которая позволяет запустить в среде Linux любую другую ОС, например Windows. Можно, наоборот, создать эмулятор, .ботающий в среде Windows, который позволит смоделировать компьютер, ботающий под управлением любой ОС, в том числе и под Linux.

жим образом, термин операционная среда означает соответствующий ин-Рфейс, необходимый программам для обращения к ОС с целью получить определенный сервис¹ — выполнить операцию ввода/вывода, получить или освободить участок памяти и т. д. 3. Система программирования на рис. 1 представлена прежде всего такими компонентами, как транслятор с соответствующего языка, библиотеки подпро­грамм, редакторы, компоновщики и отладчики. Не бывает самостоятельных (оторванных от ОС) систем программирования. Любая система программи­рования может работать только в соответствующей ОС, под которую она создана, однако при этом она может позволять разрабатывать программное обеспечение и под другие ОС. Например, одна из популярных систем про­граммирования на языке C/C++ от фирмы Watcom для OS/2 позволяет по­лучать программы и для самой OS/2, и для DOS, и для Windows. В том случае, когда создаваемые программы должны работать совсем на другой аппаратной базе, говорят о кросс-системах. Так, для ПК на базе микропроцес­соров семейства i80x86 имеется большое количество кросс-систем, позволяю,-щих создавать программное обеспечение для различных микропроцессоров и микроконтроллеров. 4. Наконец, под утилитами понимают специальные системные программы, с по­мощью которых можно как обслуживать саму операционную систему, так и подготавливать для работы носители данных, выполнять перекодирование данных, осуществлять оптимизацию размещения данных на носителе и про­изводить некоторые другие работы, связанные с обслуживанием вычислитель­ной системы. К утилитам следует отнести и программу разбиения накопителя на магнитных дисках на разделы, и программу форматирования, и программу переноса основных системных файлов самой ОС. Также к утилитам относят­ся и небезызвестные комплексы программ от фирмы Symantec, носящие имя Питера Нортона (создателя этой фирмы и соавтора популярного набора ути­лит для первых IBM PC). Естественно, что утилиты могут работать только в соответствующей операционной среде.

Сервис (service) - обслуживание, выполнение соответствующего запроса.

имеет почти то же значение. Разница между ними объясняется в той главе, в которой даются точные определения этим понятиям; здесь же можно только сказать, что «транслятор» — понятие более широкое, а «компилятор» — более уз­кое (любой компилятор является транслятором, но не наоборот).

Традиционная архитектура компьютера (архитектура фон Неймана) остается неизменной и преобладает в современных вычислительных системах. Столь же неизменными остаются и базовые принципы, на основе которых строятся сред­ства разработки программного обеспечения для компьютеров — трансляторы, компиляторы и интерпретаторы. Видимо, этим объясняется практически полное отсутствие современных публикаций в этой области, а те, что известны, являют­ся не достаточно широко доступными (автор может выделить книги и публика­ции [4, 13, 18, 26, 27, 35, 40, 45, 47]). Тем не менее современные средства разра­ботки, оставаясь на тех же базовых принципах, что и компьютеры традиционной архитектуры, прошли долгий путь совершенствования и развития от командных систем до интегрированных сред и систем программирования. И это обстоятель­ство нашло отражение в предлагаемом учебном пособии.

Ныне существует огромное количество разнообразных языков программирова­ния. Все они имеют свою историю, свою область применения, и перечислять даже наиболее известные из них здесь не имеет смысла. Но все эти языки по­строены на основе одних и тех же принципов, основы которых определяет тео­рия формальных языков и грамматик. Именно теоретическим основам посвящены четыре первые главы пособия, поскольку для построения транслятора необходи­мо знать все те принципы, на основе которых он работает. Первая глава посвя­щена общим принципам и определениям, на которых построена теория формаль­ных языков и грамматик; вторая глава посвящена регулярным языкам, а третья и четвертая — контекстно-свободным языкам и грамматикам.

В пятой и шестой главах рассматривается работа компилятора как генератора кода результирующей программы. Она рассматривается с точки зрения сущест­вующих примеров и методов реализации, поскольку семантика языков програм­мирования и генерация кода, к сожалению, не основаны на столь же «красивом», математически обоснованном аппарате, как анализ текста исходной программы в компиляторе.

Наконец, все современные компиляторы являются составной частью системного программного обеспечения. Они составляют основу всех современных средств разработки как прикладных, так и системных программ. Принципы организации и структура современных систем программирования рассматриваются в послед­ней (седьмой) главе. Там же приводятся примеры некоторых современных сис­тем программирования с разъяснением принципов, положенных в их основу.

2. Формальные языки и грамматики. Способы задания языков. символов. Операции над цепочками символов. Понятие языка. Способы задания языков. Синтаксис и семантика языка. Особенности языков программирования.

Цепочки символов. Операции над цепочками символов

Цепочкой символов (или строкой ) называют произвольную последовательность символов, записанных один за другим. Понятие символа (или буквы) является базовым в теории формальных языков и не нуждается в определении.

Далее цепочки символов будем обозначать греческими буквами: а, р\ у.

Итак, цепочка — это последовательность, в которую могут входить любые допус­тимые символы. Строка, которую вы сейчас читаете, является примером цепочки, допустимые символы в которой — строчные и заглавные русские буквы, знаки препинания и символ пробела. Но цепочка — это необязательно некоторая ос­мысленная последовательность символов. Последовательность «аввв.лагрьъ ,.лл» — тоже пример цепочки символов.

Для цепочки символов важен состав и количество символов в ней, а также поря­док символов в цепочке. Один и тот же символ может произвольное число раз входить в цепочку. Поэтому цепочки «а» и «аа», а также «аб» и «ба» — это раз­личные цепочки символов. Цепочки символов аир равны (совпадают), а = р, если они имеют один и тот же состав символов, одно и то же их количество и одинаковый порядок следования символов в цепочке.

Количество символов в цепочке называют длиной цепочки. Длина цепочки сим­волов а обозначается как |а|. Очевидно, что если а = р, то и |А| = |В|.

Основной операцией над цепочками символов является операция конкатенации (объединения или сложения) цепочек.

Конкатенация (сложение, объединение) двух цепочек символов — это дописы­вание второй цепочки в конец первой. Конкатенация цепочек аир обозначает­ся как ар. Выполнить конкатенацию цепочек просто: например, если а = «аб», а р = «вг», то ар = «абвг».

Так как в цепочке важен порядок символов, то очевидно, что операция конкате­нации не обладает свойством коммутативности, то есть в общем случае Заир такие, что ар*ра. Также очевидно, что конкатенация обладает свойством ассо­циативности, то есть (аР)у = а(Ру). Можно выделить еще две операции над цепочками.

Обращение цепочки — это запись символов цепочки в обратном порядке. Обра­щение цепочки а обозначается как a^R. Если a = «абвг», то a^R = «гвба». Для опе­рации обращения справедливо следующее равенство V a,p: (aP)^R = p^Ra^R.

Итерация (повторение) цепочки п раз, где neN, n > 0 — это конкатенация це­почки самой с собой п раз. Итерация цепочки a n раз обозначается как aⁿ. Для операции повторения справедливы следующие равенства V а: а¹ = а, а² = аа, а³ = ааа, ... и т. д.

Среди всех цепочек символов выделяется одна особенная — пустая цепочка. Пустая цепочка символов — это цепочка, не содержащая ни одного символа. Пустую цепочку здесь везде будем обозначать греческой буквой А, (в литературе ее иногда обозначают латинской буквой е или греческой г).

Для пустой цепочки справедливы следующие равенства:

1. N = 0;

2. Va: Ха = аХ = а;

3. X^R = X;

4. \/п>0:Х^п = Х;

5. Va:a°=l.

Понятие языка. Формальное определение языка

В общем случае язык — это заданный набор символов и правил, устанавливаю­щих способы комбинации этих символов между собой для записи осмысленных текстов. Основой любого естественного или искусственного языка является ал­фавит, определяющий набор допустимых символов языка.

Алфавит — это счетное множество допустимых символов языка. Будем обозна­чать это множество символом V. Интересно, что согласно формальному опре­делению, алфавит не обязательно должен быть конечным (перечислимым) мно­жеством, но реально все существующие языки строятся на основе конечных алфавитов.

Цепочка символов а является цепочкой над алфавитом V: a(V), если в нее вхо­дят только символы, принадлежащие множеству символов V. Для любого алфа­вита V пустая цепочка X может как являться, так и не являться цепочкой Х(У). Это условие оговаривается дополнительно

Если V — некоторый алфавит, то:

• V⁺ — множество всех цепочек над алфавитом V без X;

• V* — множество всех цепочек над алфавитом V, включая А,.

Справедливо равенство: V* = V⁺ u {X}.

Языком L над алфавитом V:L(V) называется некоторое счетное подмножес цепочек конечной длины из множества всех цепочек над алфавитом V. Из эп определения следуют два вывода: во-первых, множество цепочек языка не обя но быть конечным; во-вторых, хотя каждая цепочка символов, входящая в яз: обязана иметь конечную длину, эта длина может быть сколь угодно больше формально ничем не ограничена.

Все существующие языки подпадают под это определение. Большинство реа ных естественных и искусственных языков содержат бесконечное множество почек. Также в большинстве языков длина цепочки ничем не ограничена (нап мер, этот длинный текст — пример цепочки символов русского языка). Цепо¹ символов, принадлежащую заданному языку, часто называют предложением язь а множество цепочек символов некоторого языка L(V) — множеством предло: ний этого языка.

Для любого языка L(V) справедливо: L(V) с V*.

Язык L(V) включает в себя язык L'(V): L'(V)cL(V), если V aeL(V): aeL'( Множество цепочек языка L'(V) является подмножеством множества цепо языка L(V) (или эти множества совпадают). Очевидно, что оба языка доля строится на основе одного и того же алфавита.

Два языка L(V) и L'(V) совпадают (эквивалентны): L'(V) = L(V), если L'(V)cL и L(V)cL'(V); или, что то же самое: V aeL'(V): aeL(V) и V aeL'(V): aeL( Множества допустимых цепочек символов для эквивалентных языков доля быть равны.

Два языка L(V) и L'(V) почти эквивалентны: L'(V) = L(V), если L'(V)u{/ = L(V)u{A.}. Множества допустимых цепочек символов почти эквивалент языки могут различаться только на пустую цепочку символов.

Способы задания языков

Итак, каждый язык — это множество цепочек символов над некоторым алфавитом. Но кроме алфавита язык предусматривает и задание правил построения пустимых цепочек, поскольку обычно далеко не все цепочки над заданным алфавитом принадлежат языку. Символы могут объединяться в слова или лексем элементарные конструкции языка, на их основе строятся предложения — сложные конструкции. И те и другие в общем виде являются цепочками сил лов, но предусматривают некоторые правила построения. Таким образом, необходимо указать эти правила, или, строго говоря, задать язык.

Язык задать можно тремя способами:

1. Перечислением всех допустимых цепочек языка.

2. Указанием способа порождения цепочек языка (заданием грамматики языка)

3. Определением метода распознавания цепочек языка.

Первый из методов является чисто формальным и на практике не применяется, так как большинство языков содержат бесконечное число допустимых цепочек и перечислить их просто невозможно. Трудно себе представить, чтобы появи­лась возможность перечислить, например, множество всех правильных текстов на русском языке или всех правильных программ на языке Pascal. Иногда, для чисто формальных языков, можно перечислить множество входящих в них цепо­чек, прибегнув к математическим определениям множеств. Однако этот метод уже стоит ближе ко второму способу.

Например, запись Ц{0,1}) = {0ⁿlⁿ, n > 0} задает язык над алфавитом V п {0,1}, со­держащий все последовательности с чередующимися символами 0 и 1, начинаю­щиеся с 0 и заканчивающиеся 1. Видно, что пустая цепочка символов в этот язык не входит. Если изменить условие в этом определении с п > 0 на п>0, то получим почти эквивалентный язык L'({0,1}), содержащий пустую цепочку.

Второй способ предусматривает некоторое описание правил, с помощью кото­рых строятся цепочки языка. Тогда любая цепочка, построенная с помощью этих правил из символов алфавита языка, будет принадлежать заданному языку. На­пример, с правилами построения цепочек символов русского языка вы долго и упорно знакомились в средней школе.

Третий способ предусматривает построение некоторого логического устройства (распознавателя) — автомата, который на входе получает цепочку символов, а на выходе выдает ответ: принадлежит или нет эта цепочка заданному языку. На­пример, читая этот текст, вы сейчас в некотором роде выступаете в роли распо­знавателя (надеюсь, что ответ о принадлежности текста русскому языку будет положительным).

Синтаксис и семантика языка

Говоря о любом языке, можно выделить его синтаксис и семантику. Кроме того, трансляторы имеют дело также с лексическими конструкциями (лексемами), ко­торые задаются лексикой языка. Ниже даны определения для всех этих понятий.

Синтаксис языка — это набор правил, определяющий допустимые конструкции языка. Синтаксис определяет «форму языка» — задает набор цепочек символов, которые принадлежат языку. Чаще всего синтаксис языка можно задать в виде строгого набора правил, но полностью это утверждение справедливо только для чисто формальных языков. Даже для большинства языков программирования набор заданных синтаксических конструкций нуждается в дополнительных по­яснениях, а синтаксис языков естественного общения вполне соответствует об­щепринятому мнению о том, что «исключения только подтверждают правило».

Например, любой окончивший среднюю школу может сказать, что строка «3+2» является арифметическим выражением, а «3 2 +» — не является. Правда, не каж­дый задумается при этом, что он оперирует синтаксисом алгебры.

Семантика языка — это раздел языка, определяющий значение предложений языка. Семантика определяет «содержание языка» — задает значение для всех допустимых цепочек языка. Семантика для большинства языков определяется неформальными методами (отношения между знаками и тем, что они обозначают, изучаются семиотикой). Чисто формальные языки лишены какого-либо смыс/ Возвращаясь к примеру, приведенному выше, и используя семантику алгебр мы можем сказать, что строка «3 + 2» есть сумма чисел 3 и 2, а также то, ч «3 + 2 - 5» — это истинное выражение. Однако изложить любому ученику си таксис алгебры гораздо проще, чем ее семантику, хотя в данном случае семант ку как раз можно определить формально.

Лексика — это совокупность слов (словарный запас) языка. Слово или лексическая единица (лексема) языка — это конструкция, которая состоит из элементов алфавита языка и не содержит в себе других конструкций. Иначе говоря, лексическая единица может содержать только элементарные символы и не может с держать других лексических единиц.

Лексическими единицами (лексемами) русского языка являются слова русского языка, а знаки препинания и пробелы представляют собой разделители, не образующие лексем. Лексическими единицами алгебры являются числа, знаки математических операций, обозначения функций и неизвестных величин. В язьи программирования лексическими единицами являются ключевые слова, идет фикаторы, константы, метки, знаки операций; в них также существуют и раз, лители (запятые, скобки, точки с запятой и т. д.).

Особенности языков программирования

Языки программирования занимают некоторое промежуточное положение между формальными и естественными языками. С формальными языками их of единяют строгие синтаксические правила, на основе которых строятся пред. жения языка. От языков естественного общения в языки программирования решли лексические единицы, представляющие основные ключевые слова (чаще всего это слова английского языка, но существуют языки программирования чьи ключевые слова заимствованы из русского и других языков). Кроме того, алгебры языки программирования переняли основные обозначения математи ских операций, что также делает их более понятными человеку. Для задания языка программирования необходимо решить три вопроса:

• определить множество допустимых символов языка;

• определить множество правильных программ языка;

• задать смысл для каждой правильной программы.

Только первые два вопроса полностью или частично удается решить с помоп

теории формальных языков.

Первый вопрос решается легко. Определяя алфавит языка, мы автоматиче

определяем множество допустимых символов. Для языков программирова:

алфавит — это чаще всего тот набор символов, которые можно ввести с юш

туры. Основу его составляет младшая половина таблицы международной кс

ровки символов (таблицы ASCII), к которой добавляются символы национ;

ных алфавитов.

Второй вопрос решается в теории формальных языков только частично. ,

всех языков программирования существуют правила, определяющие синтаь

языка, но как уже было сказано, их недостаточно для того, чтобы строго опре­делить все возможные синтаксические конструкции. Дополнительные ограниче­ния накладываются семантикой языка. Эти ограничения оговариваются в не­формальной форме для каждого отдельного языка программирования. К таким ограничениям можно отнести необходимость предварительного описания пере­менных и функций, необходимость соответствия типов переменных и констант в выражениях, формальных и фактических параметров в вызовах функций и др.

Отсюда следует, что практически все языки программирования, строго говоря, не являются формальными языками. И именно поэтому во всех трансляторах, кроме синтаксического разбора и анализа предложений языка, дополнительно предусмотрен семантический анализ.

Третий вопрос в принципе не относится к теории формальных языков, посколь­ку, как уже было сказано, такие языки лишены какого-либо смысла. Для ответа на него нужно использовать другие подходы. В качестве таких подходов можно указать следующие:

• изложить смысл программы, написанной на языке программирования, на дру­гом языке, более понятном тому, кому адресована программа;

• использовать для проверки смысла некоторую «идеальную машину», которая предназначена для выполнения программ, написанных на данном языке.

Все, кто писал программы, так или иначе обязательно использовали первый под­ход. Комментарии в хорошей программе — это и есть изложение ее смысла. По­строение блок-схемы, а равно любое другое описание алгоритма программы — это тоже способ изложить смысл программы на другом языке (например, языке графических символов блок-схем алгоритмов, смысл которого в свою очередь, изложен в соответствующем ГОСТе). Да и документация к программе — тоже способ изложения ее смысла. Но все эти способы ориентированы на человека, которому они, конечно же, более понятны. Однако не существует пока универ­сального способа проверить, насколько описание соответствует программе.

Машина же понимает только один язык — язык машинных команд. Но изложить программу на языке машинных команд — задача слишком трудоемкая для чело­века, как раз для ее решения и создаются трансляторы.

Второй подход используется при отладке программы. Оценку же результатов выполнения программы при отладке выполняет человек. Любые попытки пору­чить это дело машине лишены смысла вне контекста решаемой задачи.

Например, предложение в программе на языке Pascal вида: i:=0; while i=0 do i:=0; может быть легко оценено любой машиной как бессмысленное. Но если в задачу входит обеспечить взаимодействие с другой параллельно выполняемой программой или, например, просто проверить надежность и долговечность про­цессора или какой-то ячейки памяти, то это же предложение покажется уже не лишенным смысла.

Некоторые успехи в процессе проверки осмысленности программ достигнуты в рамках систем автоматизации разработки программного обеспечения (CASE-системы). Их подход основан на проектировании сверху вниз — от описания за­дачи на языке, понятном человеку, до перевода ее в операторы языка программирования. Но такой подход выходит за рамки возможностей трансляторов, поэто­му здесь рассматриваться не будет.

Однако разработчикам компиляторов так или иначе приходится решать вопрос о смысле программ. Во-первых, компилятор должен все-таки преобразовать исходную программу в последовательность машинных команд, а для этого ему необходимо иметь представление о том, какая последовательность команд соот­ветствует той или иной части исходной программы. Обычно такие последова­тельности сопоставляются базовым конструкциям входного языка (далее будет рассмотрено, как это можно сделать). Здесь используется первый подход к изло­жению смысла программы. Во-вторых, многие современные компиляторы по­зволяют выявить сомнительные с точки зрения смысла места в исходной про­грамме — такие, как недостижимые операторы, неиспользуемые переменные, неопределенные результаты функций и т. п. Обычно компилятор указывает та­кие места в виде дополнительных предупреждений, которые разработчик может принимать или не принимать во внимание. Для достижения этой цели компиля­тор должен иметь представление о том, как программа будет выполняться — используется второй подход. Но в обоих случаях осмысление исходной програм­мы закладывает в компилятор его создатель (или коллектив создателей) — то есть человек, который руководствуется неформальными методами (чаще всего, описанием входного языка). В теории формальных языков вопрос о смысле про­грамм не решается.

Итак, на основании изложенных положений можно сказать, что возможности трансляторов по проверке осмысленности предложений входного языка сильно ограничены, практически даже равны нулю. Именно поэтому большинство из них в лучшем случае ограничиваются рекомендациями разработчикам по тем местам исходного текста программ, которые вызывают сомнения с точки зрения смысла. Поэтому большинство трансляторов обнаруживает только незначитель­ный процент от общего числа смысловых («семантических») ошибок, а следова­тельно, подавляющее число такого рода ошибок всегда, к большому сожалению, остается на совести автора программы.

3. Определение грамматики. Форма Бэкуса-Наура. Принцип рекурсии в правилах грамматики. Другие способы задания грамматик.

Определение грамматики. Форма Бэкуса—Наура

Понятие о грамматике языка

Грамматика — это описание способа построения предложений некоторого язы­ка. Иными словами, грамматика — это математическая система, определяющая язык.

Фактически, определив грамматику языка, мы указываем правила порождения цепочек символов, принадлежащих этому языку. Таким образом, грамматика — это генератор цепочек языка. Она относится ко второму способу определения языков — порождению цепочек символов. Грамматику языка можно описать различными способами; например, грамма-гика русского языка описывается довольно сложным набором правил, которые изучают в начальной школе. Но для многих языков (и для синтаксической части гзыков программирования в том числе) допустимо использовать формальное шисание грамматики, построенное на основе системы правил (или продукций).

Правило (или продукция) — это упорядоченная пара цепочек символов (а,(3). В правилах очень важен порядок цепочек, поэтому их чаще записывают в виде х->(3 (или а::=Р). Такая запись читается как «а порождает р» или «(3 по опреде­лению есть а».

Грамматика языка программирования содержит правила двух типов: первые ^определяющие синтаксические конструкции языка) довольно легко поддают-;я формальному описанию; вторые (определяющие семантические ограничения ?зыка) обычно излагаются в неформальной форме. Поэтому любое описание ^или общепринятый стандарт) языка программирования обычно состоит из двух частей: вначале формально излагаются правила построения синтаксических кон-:трукций, а потом на естественном языке дается описание семантических пра­вил. Естественный язык понятен человеку, пользователю, который будет писать программы на языке программирования; для компилятора же семантические эграничения необходимо излагать в виде алгоритмов проверки правильности про­граммы (речь, как уже было сказано выше, не идет о смысле программ, а только лишь о семантических ограничениях на исходный текст). Такой проверкой в компиляторе занимается семантический анализатор — специально для этого раз­работанная часть компилятора.

Далее, говоря о грамматиках языков программирования, будем иметь в виду только правила построения синтаксических конструкций языка. Однако следует помнить, что грамматика любого языка программирования в общем случае не ог­раничивается только этими правилами.

Язык, заданный грамматикой G, обозначается как L(G).

Две грамматики G и G' называются эквивалентными, если они определяют один и тот же язык: L(G) = L(G'). Две грамматики G и G' называются почти эквива­лентными, если заданные ими языки различаются не более чем на пустую цепоч­ку символов: L(G) u {A,} = L(G') и {Ц.

Формальное определение грамматики. Форма Бэкуса—Наура

Для полного формального определения грамматики кроме правил порождения цепочек языка необходимо задать также алфавит языка.

Формально грамматика G определяется как четверка G(VT,VN,P,S), где:

• VT — множество терминальных символов;

• VN — множество нетерминальных символов: VNnVT = 0;

Р — множество правил (продукций) грамматики вида а-»р, где aeV⁺, PeV*; Q S- целевой (начальный) символ грамматики SeVN. Множество V = VNuVT называют полным алфавитом грамматики G.

Рассмотрим множества VN и VT. Множество терминальных символов VT содер­жит символы, которые входят в алфавит языка, порождаемого грамматикой. Как правило, символы из множества VT встречаются только в цепочках правых час­тей правил, если же они встречаются в цепочке левой части правила, то обязаны быть и в цепочке правой его части. Множество нетерминальных символов VN содержит символы, которые определяют слова, понятия, конструкции языка. Каж­дый символ этого множества может встречаться в цепочках как левой, так и пра­вой частей правил грамматики, но он обязан хотя бы один раз быть в левой час­ти хотя бы одного правила. Правила грамматики строятся так, чтобы в левой части каждого правила был хотя бы один нетерминальный символ.

Эти два множества не пересекаются: каждый символ может быть либо терми­нальным, либо нетерминальным. Ни один символ в алфавите грамматики не может быть нетерминальным и терминальным одновременно. Целевой символ грамматики — это всегда нетерминальный символ.

Во множестве правил грамматики может быть несколько правил, имеющих оди­наковые правые части, вида: а->р₍, ач>р₂, ... а->р_п. Тогда эти правила объединя­ют вместе и записывают в виде: a—>p₁|p₂|—lPn • Одной строке в такой записи соот­ветствует сразу правил.

Такую форму записи правил грамматики называют формой Бэкуса—Наура. Форма Бэкуса—Наура предусматривает, как правило, также, что нетерминальные сим­волы берутся в угловые скобки: < >. Иногда знак «->» в правилах грамматики заменяют на знак «::=» (что характерно для старых монографий), но это всего лишь незначительные модификации формы записи, не влияющие на ее суть.

Ниже приведен пример грамматики для целых десятичных чисел со знаком:

G({0,1.2.3.4.5.6.7.8.9.-.+}.{<число>.<чс>,<цифра>},Р.<число>) Р:

<число> -» <чс> | +<чс> | -<чс>

<чс> -> <цифра> | <чс><цифра>

<цифра> ->0|1|2|3|4|5|6|7|8|9

Рассмотрим составляющие элементы грамматики G:

• множество терминальных символов VT содержит двенадцать элементов: де­сять десятичных цифр и два знака;

• множество нетерминальных символов VN содержит три элемента: символы <число>, <чс> и <цифра>;

• множество правил содержит 15 правил, которые записаны в три строки (то есть имеются только три различных правых части правил);

• целевым символом грамматики является символ <число>.

Следует отметить, что символ <чс> — это бессмысленное сочетание букв русско­го языка, но это обычный нетерминальный символ грамматики, такой же, как и два других. Названия нетерминальных символов не обязаны быть осмысленны­ми, это сделано просто для удобства понимания правил грамматики человеком. В принципе в любой грамматике можно полностью изменить имена всех нетер-минальных символов, не меняя при этом языка, заданного грамматикой, — точно также, например, в программе на языке Pascal можно изменить имена идентифи­каторов, и при этом не изменится смысл программы.

Для терминальных символов это неверно. Набор терминальных символов всегда строго соответствует алфавиту языка, определяемого грамматикой.

Бот, например, та же самая грамматика для целых десятичных чисел со знаком, в которой нетерминальные символы обозначены большими латинскими буквами (далее это будет часто применяться в примерах):

G'({0.1.2.3.4.5.6.7.8.9,-.+}.{S,T.F}.P,S)

Р:

S -» Т | +Т | -Т

Т -> F | TF

F-»0|l|2|3|4|5|6|7|8|9

Здесь изменилось только множество нетерминальных символов. Теперь VN = = {S,T,F}. Язык, заданный грамматикой, не изменился — грамматики G и G' эк­вивалентны.

Принцип рекурсии в правилах грамматики

Особенность формальных грамматик в том, что они позволяют определить бес­конечное множество цепочек языка с помощью конечного набора правил (конеч­но, множество цепочек языка тоже может быть конечным, но даже для простых реальных языков это условие обычно не выполняется). Приведенная выше в примере грамматика для целых десятичных чисел со знаком определяет беско­нечное множество целых чисел с помощью 15 правил.

Возможность пользоваться конечным набором правил достигается в такой фор­ме записи грамматики за счет рекурсивных правил. Рекурсия в правилах грам­матики выражается в том, что один из нетерминальных символов определяется сам через себя. Рекурсия может быть непосредственной (явной) — тогда символ определяется сам через себя в одном правиле, либо косвенной (неявной) — тогда то же самое происходит через цепочку правил.

В рассмотренной выше грамматике G непосредственная рекурсия присутствует в правиле: <чс>-»<чс><цифра>, а в эквивалентной ей грамматике G' — в правиле: T-»TF.

Чтобы рекурсия не была бесконечной, для участвующего в ней нетерминального символа грамматики должны существовать также и другие правила, которые оп­ределяют его, минуя самого себя, и позволяют избежать бесконечного рекурсив­ного определения (в противном случае этот символ в грамматике был бы просто не нужен). Такими правилами являются <чс>-»<цифра> — в грамматике G и T-»F — в грамматике G'.

• В теории формальных языков более ничего сказать о рекурсии нельзя. Но, чтобы полнее понять смысл рекурсии, можно прибегнуть к семантике языка — в рас­смотренном выше примере это язык целых десятичных чисел со знаком. Рас­смотрим его смысл.

Если попытаться дать определение тому, что же является числом, то начать мож­но с того, что любая цифра сама по себе есть число. Далее можно заметить, что любые две цифры — это тоже число, затем — три цифры и т. д. Если строить определение числа таким методом, то оно никогда не будет закончено (в матема­тике разрядность числа ничем не ограничена). Однако можно заметить, что каж­дый раз, порождая новое число, мы просто дописываем цифру справа (посколь­ку привыкли писать слева направо) к уже написанному ряду цифр. А этот ряд цифр, начиная от одной цифры, тоже в свою очередь является числом. Тогда определение для понятия «число» можно построить таким образом: «число — это любая цифра, либо другое число, к которому справа дописана любая цифра». Именно это и составляет основу правил грамматик G и G' и отражено во второй строке правил в правилах <чс>—><цифра> j <чс><цифра> и T-»F|TF. Другие правила в этих грамматиках позволяют добавить к числу знак (первая строка правил) и дают определение понятию «цифра» (третья строка правил). Они элементарны и не требуют пояснений.

Принцип рекурсии (иногда его называют «принцип итерации», что не меняет сути) — важное понятие в представлении о формальных грамматиках. Так или иначе, явно или неявно рекурсия всегда присутствует в грамматиках любых ре­альных языков программирования. Именно она позволяет строить бесконечное множество цепочек языка, и говорить об их порождении невозможно без пони­мания принципа рекурсии. Как правило, в грамматике реального языка програм­мирования содержится не одно, а целое множество правил, построенных с помо­щью рекурсии.

Другие способы задания грамматик

Форма Бэкуса—Наура — удобный с формальной точки зрения, но не всегда дос­тупный для понимания способ записи формальных грамматик. Рекурсивные определения хороши для формального анализа цепочек языка, но не удобны с точки зрения человека. Например, то, что правила <чс>—><цифра> | <чс><цифра> отражают возможность для построения числа дописывать справа любое число цифр, начиная от одной, неочевидно и требует дополнительного пояснения.

Но при создании языка программирования важно, чтобы его грамматику пони­мали не только те, кому предстоит создавать компиляторы для этого языка, но и пользователи языка — будущие разработчики программ. Поэтому существуют другие способы описания правил формальных грамматик, которые ориентирова­ны на большую понятность человеку.

Далее рассмотрим два наиболее распространенных из этих способов: запись пра­вил грамматик с использованием метасимволов и запись правил грамматик в графическом виде.

Запись правил грамматик

с использованием метасимволов

Запись правил грамматик с использованием метасимволов предполагает, что в строке правила грамматики могут встречаться специальные символы — мега-символы, — которые имеют особый смысл и трактуются специальным образом. В качестве таких метасимволов чаще всего используются следующие символы: (круглые скобки), (квадратные скобки), (фигурные скобки), (запя­тая) и "" (кавычки).

Эти метасимволы имеют следующий смысл:

• круглые скобки означают, что из всех перечисленных внутри них цепочек символов в данном месте правила грамматики может стоять только одна це­почка;

• квадратные скобки означают, что указанная в них цепочка может встречать­ся, а может и не встречаться в данном месте правила грамматики (то есть мо­жет быть в нем один раз или ни одного раза);

• фигурные скобки означают, что указанная внутри них цепочка может не встре­чаться в данном месте правила грамматики ни одного раза, встречаться один раз или сколь угодно много раз;

• запятая служит для того, чтобы разделять цепочки символов внутри круглых скобок;

О кавычки используются в тех случаях, когда один из метасимволов нужно включить в цепочку обычным образом — то есть когда одна из скобок или за­пятая должны присутствовать в цепочке символов языка (если саму кавычку нужно включить в цепочку символов, то ее надо повторить дважды — этот принцип знаком разработчикам программ).

Вот как должны выглядеть правила рассмотренной выше грамматики G, если их записать с использованием метасимволов:

<число> -» [(+.-)]<цифра>{<цифра>}

<цифра> ->0|1|2|3|4|5|6|7|8|9

Вторая строка правил не нуждается в комментариях, а первое правило читается так: «число есть цепочка символов, которая может начинаться с символов + или - должна содержать дальше одну цифру, за которой может следовать последова­тельность из любого количества цифр». В отличие от формы Бэкуса—Наура, в форме записи с помощью метасимволов, как видно, во-первых, убран из грам­матики малопонятный нетерминальный символ <чс>, а во-вторых — удалось пол­ностью исключить рекурсию. Грамматика в итоге стала более понятной.

Форма записи правил с использованием метасимволов — это удобный и понят­ный способ представления правил грамматик. Она во многих случаях позволяет полностью избавиться от рекурсии, заменив ее символом итерации (фигур­ные скобки). Как будет понятно из дальнейшего материала, эта форма наиболее употребительна для одного из типов грамматик — регулярных грамматик.

Запись правил грамматик в графическом виде

При записи правил в графическом виде вся грамматика представляется в форме набора специальным образом построенных диаграмм. Эта форма была предло­жена при описании грамматики языка Pascal, а затем она получила широкое рас­пространение в литературе. Она доступна не для всех типов грамматик, а толькодля контекстно-свободных и регулярных типов, но этого достаточно, чтобы ее можно было использовать для описания грамматик известных языков програм­мирования.

В такой форме записи каждому нетерминальному символу грамматики соответ­ствует диаграмма, построенная в виде направленного графа. Граф имеет следую­щие типы вершин:

• точка входа (на диаграмме никак не обозначена, из нее просто начинается входная дуга графа);

• нетерминальный символ (на диаграмме обозначается прямоугольником, в ко­торый вписано обозначение символа);

• цепочка терминальных символов (на диаграмме обозначается овалом, кругом или прямоугольником с закругленными краями, внутрь которого вписана це­почка);

• узловая точка (на диаграмме обозначается жирной точкой или закрашенным кружком);

• точка выхода (никак не обозначена, в нее просто входит выходная дуга графа).

Каждая диаграмма имеет только одну точку входа и одну точку выхода, но сколь­ко угодно вершин других трех типов. Вершины соединяются между собой на­правленными дугами графа (линиями со стрелками). Из входной точки дуги могут только выходить, а во входную точку — только входить. В остальные вер­шины дуги могут как входить, так и выходить (в правильно построенной грам­матике каждая вершина должна иметь как минимум один вход и как минимум один выход).

Чтобы построить цепочку символов, соответствующую какому-либо нетерми­нальному символу грамматики, надо рассмотреть диаграмму для этого символа. Тогда, начав движение от точки входа, надо двигаться по дугам графа диаграммы через любые вершины вплоть до точки выхода. При этом, проходя через верши­ну, обозначенную нетерминальным символом, этот символ следует поместить в результирующую цепочку. При прохождении через вершину, обозначенную цепочкой терминальных символов, эти символы также следует поместить в ре­зультирующую цепочку. При прохождении через узловые точки диаграммы над результирующей цепочкой никаких действий выполнять не надо. Через любую вершину графа диаграммы, в зависимости от возможного пути движения, можно пройти один раз, ни разу или сколь угодно много раз. Как только мы попадем в точку выхода диаграммы, построение результирующей цепочки закончено.

Результирующая цепочка, в свою очередь, может содержать нетерминальные символы. Чтобы заменить их на цепочки терминальных символов, нужно, опять же, рассматривать соответствующие им диаграммы. И так до тех пор, пока в це­почке не останутся только терминальные символы. Очевидно, что для того, что­бы построить цепочку символов заданного языка, надо начать рассмотрение с диаграммы целевого символа грамматики.

Это удобный способ описания правил грамматик, оперирующий образами, а по­тому ориентированный исключительно на людей. Даже простое изложение его основных принципов здесь оказалось довольно громоздким, в то время как суть

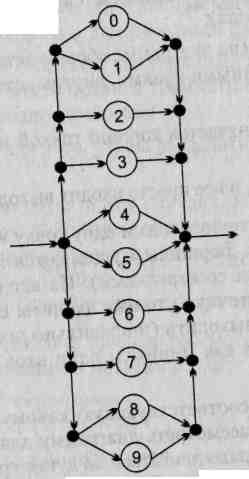
Рис. 9.1. Графическое представление грамматики целых десятичных чисел со знаком: вверху — для понятия «число»; внизу — для понятия «цифра»

Как уже было сказано выше, данный способ в основном применяется в литерату­ре при изложении грамматик языков программирования. Для пользователей — разработчиков программ — он удобен, но практического применения в компиля­торах пока не имеет.

Классификация языков и грамматик

Выше уже упоминались различные типы грамматик, но не было указано, как и по какому принципу они подразделяются на типы. Для человека языки быва­ют простые и сложные, но это сугубо субъективное мнение, которое зачастую за­висит от личности человека.

Для компиляторов языки также можно разделить на простые и сложные, но в данном случае существуют жесткие критерии для этого разделения. Как будет показано далее, от того, к какому типу относится тот или иной язык програмирования, зависит сложность распознавателя для этого языка. Чем сложнее язык, тем выше вычислительные затраты компилятора на анализ цепочек исходной программы, написанной на этом языке, а следовательно, сложнее сам компиля­тор и его структура. Для некоторых типов языков в принципе невозможно по­строить компилятор, который бы анализировал исходные тексты на этих языках за приемлемое время на основе ограниченных вычислительных ресурсов (имен­но поэтому до сих пор невозможно создавать программы на естественных язы­ках/например на русском или английском).

Классификация грамматик.

Четыре типа грамматик по Хомскому

Формальные грамматики классифицируются по структуре их правил. Если все без исключения правила грамматики удовлетворяют некоторой заданной струк­туре, то ее относят к определенному типу. Достаточно иметь в грамматике одно правило, не удовлетворяющее требованиям структуры правил, и она уже не по­падает в заданный тип. По классификации Хомского выделяют четыре типа грамматик.

Тип 0: грамматики с фразовой структурой

На структуру их правил не накладывается никаких ограничений: для граммати­ки вида G(VT,VN,P,S), V » VNuVT правила имеют вид: а-»р, где aeV\ (3eV*. Это самый общий тип грамматик. В него подпадают все без исключения фор­мальные грамматики, но часть из них, к общей радости, может быть также отне­сена и к другим классификационным типам. Дело в том, что грамматики, которые относятся только к типу 0 и не могут быть отнесены к другим типам, являются самыми сложными по структуре. Практического применения грамматики, относящиеся только к типу 0, не имеют.

Тип 1: контекстно-зависимые (КЗ) и неукорачивающие грамматики

В этот тип входят два основных класса грамматик.

Контекстно-зависимые грамматики G(VT,VN,P,S), V = VNuVT имеют правила вида: сцАаг-юцрсхг, где а^еУ, AeVN, PeV⁺.

Неукорачивающие грамматики G(VT,VN,P,S), V = VNu VT имеют правила вида: а->Р, где a,PeV⁺, ]p|>|a|.

Структура правил КЗ-грамматик такова, что при построении предложений за­данного ими языка один и тот же нетерминальный символ может быть заменен на ту или иную цепочку символов в зависимости от того контекста, в котором он встречается. Именно поэтому эти грамматики называют «контекстно-зависимы­ми». Цепочки а) и а₂ в правилах грамматики обозначают контекст (щ — левый контекст, а а₂ — правый контекст), в общем случае любая из них (или даже обе) Может быть пустой. Говоря иными словами, значение одного и того же символа может быть различным в зависимости от того, в каком контексте он встречаетсяНеукорачиваювдие грамматики имеют такую структуру правил, что при построе­нии предложений языка, заданного грамматикой, любая цепочка символов мо­жет быть заменена на цепочку символов не меньшей длины. Отсюда и название «неукорачивающие».

Доказано, что эти два класса грамматик эквивалентны. Это значит, что для лю­бого языка, заданного контекстно-зависимой грамматикой, можно построить неукорачивающую грамматику, которая будет задавать эквивалентный язык, и наоборот: для любого языка, заданного неукорачивающей грамматикой, мож­но построить контекстно-зависимую грамматику, которая будет задавать эквива­лентный язык.

При построении компиляторов такие грамматики не применяются, поскольку языки программирования, рассматриваемые компиляторами, имеют более про­стую структуру и могут быть построены с помощью грамматик других типов.

Тип 2: контекстно-свободные (КС) грамматики

Контекстно-свободные (КС) грамматики G(VT,VN,P,S), V = VNuVT имеют правила вида: А-»р\ где AeVN, |3eV⁺. Такие грамматики также иногда называют неукорачивающими контекстно-свободными (НКС) грамматиками (видно, что в правой части правила у них должен всегда стоять как минимум один символ).

Существует также почти эквивалентный им класс грамматик — укорачивающие контекстно-свободные (УКС) грамматики G(VT,VN,P,S), V = VNuVT, правила которых могут иметь вид: А->р\ где AeVN, PeV*.

Разница между этими двумя классами грамматик заключается лишь в том, что в УКС-грамматиках в правой части правил может присутствовать пустая це­почка (X), а в НКС-грамматиках — нет. Отсюда ясно, что язык, заданный НКС-грамматикой, не может содержать пустой цепочки. Доказано, что эти два класса грамматик почти эквивалентны. В дальнейшем, когда речь будет идти о КС-грамматиках, уже не будет уточняться, какой класс грамматики (УКС или НКС) имеется в виду, если возможность наличия в языке пустой цепочки не имеет принципиального значения.

КС-грамматики широко используются при описании синтаксических конструк­ций языков программирования. Синтаксис большинства известных языков про­граммирования основан именно на КС-грамматиках, поэтому в данном курсе им уделяется большое внимание.

Внутри типа КС-грамматик кроме классов НКС и УКС выделяют еще целое множество различных классов грамматик, и все они относятся к типу 2. Далее, когда КС-грамматики и КС-языки будут рассматриваться более подробно, на не­которые из этих классов грамматик и их характерные особенности будет обраще­но особое внимание.

Тип 3: регулярные грамматики

К типу регулярных относятся два эквивалентных класса грамматик: леволиней­ные и праволинейные.

Леволинейные грамматики G(VT,VN,P,S), V = VNuVT могут иметь правила двух видов: А-»Ву или А->у, где A,BeVN, yeVT.

В свою очередь, праволинейные грамматики G(VT,VN,P,S), V = VNuVT могут иметь правила тоже двух видов: А~-»уВ или А-»у, где A.BeVN, yeVT*.

Эти два класса грамматик эквивалентны и относятся к типу регулярных грам­матик.

Регулярные грамматики используются при описании простейших конструкций языков программирования: идентификаторов, констант, строк, комментариев и т. д. Эти грамматики исключительно просты и удобны в использовании, поэтому в компиляторах на их основе строятся функции лексического анализа входного языка (принципы их построения будут рассмотрены далее).

Типы грамматик соотносятся между собой особым образом. Из определения типов 2 и 3 видно, что любая регулярная грамматика является КС-грамматикой, но не наоборот. Также очевидно, что любая грамматика может быть отнесена и к типу 0, поскольку он не накладывает никаких ограничений на правила. В то же время существуют укорачивающие КС-грамматики (тип 2), которые не являют­ся ни контекстно-зависимыми, ни неукорачивающими (тип 1), поскольку могут содержать правила вида «А-»Ъ>, недопустимые в типе 1. В целом можно сказать, что сложность грамматики обратно пропорциональна тому максимально воз­можному номеру типа, к которому может быть отнесена грамматика. Граммати­ки, которые относятся только к типу 0, являются самыми сложными, а грамма­тики, которые можно отнести к типу 3 — самыми простыми.

Классификация языков

Языки классифицируются в соответствии с типами грамматик, с помощью кото­рых они заданы. Причем, поскольку один и тот же язык в общем случае может быть задан сколь угодно большим количеством грамматик, которые могут отно­ситься к различным классификационным типам, то для классификации самого языка среди всех его грамматик всегда выбирается грамматика с максимально возможным классификационным типом. Например, если язык L может быть за­дан грамматиками G_t и G₂, относящимися к типу (контекстно - зависимые), грамматикой G₃, относящейся к типу 2 (контекстно-свободные), и грамматикой G₄, относящейся к типу 3 (регулярные), то сам язык должен быть отнесен к типу 3 и является регулярным языком.

От классификационного типа языка зависит не только то, с помощью какой грамматики можно построить предложения этого языка, но также и то, насколь­ко сложно распознать эти предложения. Распознать предложения — значит по­строить распознаватель для языка (третий способ задания языка). Сами распо­знаватели, их структура и классификация будут рассмотрены далее, здесь же можно указать, что сложность распознавателя языка напрямую зависит от клас­сификационного типа, к которому относится язык.

Сложность языка убывает с возрастанием номера классификационного типа языка. Самыми сложными являются языки типа 0, самыми простыми — языки типа 3.

Согласно классификации грамматик, существуют также четыре типа языков.

Тип О: языки с фразовой структурой

Это самые сложные языки, которые могут быть заданы только грамматикой, от­носящейся к типу 0. Для распознавания цепочек таких языков требуются вычис­лители, равномощные машине Тьюринга. Поэтому можно сказать, что если язык относится к типу 0, то для него невозможно построить компилятор, который гарантированно выполнял бы разбор предложений языка за ограниченное время на основе ограниченных вычислительных ресурсов.

К сожалению, практически все естественные языки общения между людьми, строго говоря, относятся именно к этому типу языков. Дело в том, что структура и значение фразы естественного языка может зависеть не только от контекста данной фразы, но и от содержания того текста, где эта фраза встречается. Одно и то же слово в естественном языке может не только иметь разный смысл в зави­симости от контекста, но и играть различную роль в предложении. Именно по­этому столь велики сложности в автоматизации перевода текстов, написанных на естественных языках, а также отсутствуют (и видимо, никогда не появятся) компиляторы, которые бы воспринимали программы на основе таких языков.

Далее языки с фразовой структурой рассматриваться не будут.

Тип 1: контекстно-зависимые (КЗ) языки

Тип 1 — второй по сложности тип языков. В общем случае время на распознава­ние предложений языка, относящегося к типу 1, экспоненциально зависит от длины исходной цепочки символов.

Языки и грамматики, относящиеся к типу 1, применяются в анализе и переводе текстов на естественных языках. Распознаватели, построенные на их основе, по­зволяют анализировать тексты с учетом контекстной зависимости в предложе­ниях входного языка (но они не учитывают содержание текста, поэтому в общем случае для точного перевода с естественного языка все же требуется вмешатель­ство человека). На основе таких грамматик может выполняться автоматизиро­ванный перевод с одного естественного языка на другой, ими могут пользоваться сервисные функции проверки орфографии и правописания в языковых процес­сорах.

В компиляторах КЗ-языки не используются, поскольку языки программирова­ния имеют более простую структуру, поэтому здесь они подробно не рассматри­ваются.

Тип 2: контекстно-свободные (КС) языки

КС-языки лежат в основе синтаксических конструкций большинства современ­ных языков программирования, на их основе функционируют некоторые до­вольно сложные командные процессоры, допускающие управляющие команды цикла и условия. Эти обстоятельства определяют распространенность данного класса языков.

В общем случае время на распознавание предложений языка, относящегося к типу 1, полиномиально зависит от длины исходной цепочки символов (в зависи­мости от класса языка это либо кубическая, либо квадратичная зависимость).

Однако среди КС-языков существует много классов языков, для которых эта за­висимость линейна. Многие языки программирования можно отнести к одному из таких классов.

КС-языки подробно рассматриваются в главе «Контекстно-свободные языки» данного учебного пособия.

Тип 3: регулярные языки

Регулярные языки — самый простой тип языков. Наверное, поэтому они явля­ются самым распространенным и широко используемым типом языков в облас­ти вычислительных систем. Время на распознавание предложений регулярного языка линейно зависит от длины исходной цепочки символов.

Как уже было сказано выше, регулярные языки лежат в основе простейших кон­струкций языков программирования (идентификаторов, констант и т. п.), кро­ме того, на их основе строятся многие мнемокоды машинных команд (языки ассемблеров), а также командные процессоры, символьные управляющие коман­ды и другие подобные структуры.

Регулярные языки — очень удобное средство. Для работы с ними можно исполь­зовать регулярные множества и выражения, конечные автоматы. Регулярные языки подробно рассматриваются в следующей главе учебного пособия.

Примеры классификации языков и грамматик

Классификация языков идет от простого к сложному. Если мы имеем дело с ре­гулярным языком, то можно утверждать, что он также является и контекстно-свободным, и контекстно-зависимым, и даже языком с фразовой структурой. В то же время известно, что существуют КС-языки, которые не являются регу­лярными, и существуют КЗ-языки, которые не являются ни регулярными, ни контекстно-свободными.

Далее приводятся примеры некоторых языков указанных типов.

Рассмотрим в качестве первого примера ту же грамматику для целых десятич­ных чисел со знаком G({0,1,2,3,4_>5,6,7,8,9,-_I+},{S,T,F},P.S):

Р:

S -> Т | +Т | -Т

Т -> F | TF

F->0|1|2|3|4|5|6|7|8|9

По структуре своих правил данная грамматика G относится к контекстно-сво­бодным грамматикам (тип 2). Конечно, ее можно отнести и к типу 0, и к типу 1, но максимально возможным является именно тип 2, поскольку к типу 3 эту грамматику отнести никак нельзя: строка Т—»F | TF содержит правило Т—»TF, которое недопустимо для типа 3, и, хотя все остальные правила этому типу соот­ветствует, одного несоответствия достаточно.

Для того же самого языка (целых десятичных чисел со знаком) можно построить и другую грамматику G'({0,1,2.3,4,5,б,7,8,9,-,+}.{S,T},P.S):

Р:

S -> Т | +Т | -Т

Т -> 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ОТ | IT | 2Т | ЗТ | 4Т | 5Т | 6Т | 7Т | 8Т | 9Т

По структуре своих правил грамматика G' является праволинейной и может быть отнесена к регулярным грамматикам (тип 3).

Для этого же языка можно построить эквивалентную леволинейную грамматику (тип 3) G"({0,l_>2,3,4,5.6,7.8,9_>-,+},{SJ},P,S):

Р:

Т^₊ | - | X

S -> ТО | Т1 | Т2 | ТЗ | Т4 | Т5 | Т6 | Т7 | Т8 | Т9 | SO | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9

Следовательно, язык целых десятичных чисел со знаком, заданный грамматика­ми G, G' и G", относится к регулярным языкам (тип 3).

В качестве второго примера возьмем грамматику G₂({0,1},{A,S},P_>S) с правила­ми Р:

S -> 0А1 ОА -» 00А1 А -> X

Эта грамматика относится к типу 0. Она определяет язык, множество предложе­ний которого можно было бы записать так: L(G₂) = {0ⁿlⁿ |'n > 0}.

Для этого же языка можно построить также контекстно-зависимую грамматику G₂'({0.1},{A,S},P',S) с правилами Р":

S -t 0A1 | 01 ОА -> 00А1 | 001

Однако для того же самого языка можно использовать и контекстно-свободную грамматику G₂"({0,1},{S},P",S) с правилами Р":

S —> 0S1 | 01

Следовательно, язык L = {0ⁿlⁿ | n > 0} является контекстно-свободным (тип 2).

В третьем примере рассмотрим грамматику G₃({a,b,c},{B,C,D,S},P,S) с правила­ми Р:

S -» BD

В -> аВЬС | ab СЬ -> ЬС CD -> Dc bDc -> bcc abD -» abc

Эта грамматика относится к типу 1. Очевидно, что она является неукорачиваю-щей. Она определяет язык, множество предложений которого можно было бы за­писать так: L(G₃) = {aⁿbⁿcⁿ | n > 0}. Известно, что этот язык не является КС-язы­ком, поэтому для него нельзя построить грамматики типов 2 или 3. Язык L - {aⁿbⁿcⁿ | п > 0} является контекстно-зависимым (тип 1). Конечно, для произвольного языка, заданного некоторой грамматикой, в общем случае довольно сложно так легко определить его тип. Не всегда можно так просто построить грамматику максимально возможного типа для произвольного языка. К тому же при строгом определении типа требуется еще доказать, что две грамматики (первоначально имеющаяся и вновь построенная) эквивалентны, а также то, что не существует для того же языка грамматики с большим по номе­ру типом. Это нетривиальная задача, которую не так легко решить.

Для многих языков, и в частности для КС-языков и регулярных языков, сущест­вуют специальным образом сформулированные утверждения, которые позволя­ют проверить принадлежность языка к указанному типу. Такие утверждения (леммы) будут рассмотрены далее в соответствующих главах этого учебника. Тогда для произвольного языка достаточно лишь доказать нужное утверждение, и после этого можно точно утверждать, что данный язык относится к тому или иному типу. Преобразование грамматик в этом случае не требуется.

Тем не менее иногда возникает задача построения для имеющегося языка грам­матики более простого типа, чем данная. И даже в том случае, когда тип языка уже известен, эта задача остается нетривиальной и в общем случае не имеет фор­мального решения (проблема преобразования грамматик рассматривается далее).

Цепочки вывода. Сентенциальная форма

Вывод. Цепочки вывода

Выводом называется процесс порождения предложения языка на основе правил определяющей язык грамматики. Чтобы дать формальное определение процессу вывода, необходимо ввести еще несколько дополнительных понятий. Цепочка Р = 5_ty5₂ называется непосредственно выводимой из цепочки а = 5!(о5₂ в грамматике G(VT,VN,P,S), V = VTuVN, 8_Ь у, 5₂ е V", со е V⁺, если в граммати­ке G существует правило: ш-»у е Р. Непосредственная выводимость цепочки Р из цепочки а обозначается так: а=>р. Иными словами, цепочка р выводима из цепочки а в том случае, если можно взять несколько символов в цепочке а, заме­нить их на другие символы согласно некоторому правилу грамматики и полу­чить цепочку р. В формальном определении непосредственной выводимости любая из цепочек 5_t или 5₂ (а равно и обе эти цепочки) может быть пустой. В предельном случае вся цепочка а может быть заменена на цепочку р, тогда в грамматике G должно существовать правило: а-»Р е Р.

Цепочка Р называется выводимой из цепочки а (обозначается а=>*Р) в том слу­чае, если выполняется одно из двух условий:

• р непосредственно выводима из а (а=>Р);

• 3 у, такая, что: у выводима из а и р непосредственно выводима из у (а=>*у и у=>Р).

Это рекурсивное определение выводимости цепочки. Суть его заключается в том, что цепочка р выводима из цепочки а, если а=>р или же если можно построить последовательность непосредственно выводимых цепочек от а к р следующеговида: a^Yi^-^Yi^-^Yn^P, п>1. В этой последовательности каждая последую­щая цепочка у_{ непосредственно выводима из предыдущей цепочки ум-Такая последовательность непосредственно выводимых цепочек называется вы­водом или цепочкой вывода. Каждый переход от одной непосредственно выводи­мой цепочки к следующей в цепочке вывода называется шагом вывода. Очевидно, что шагов вывода в цепочке вывода всегда на один больше, чем промежуточных цепочек. Если цепочка р непосредственно выводима из цепочки а: а=>р, то име­ется всего один шаг вывода.

Если цепочка вывода из а к р содержит одну или более промежуточных цепочек (два или более шагов вывода), то она имеет специальное обозначение а=>+Р (го­ворят, что цепочка р нетривиально выводима из цепочки а). Если количество шагов вывода известно, то его можно указать непосредственно у знака выводи­мости цепочек. Например, запись а=>⁴Р означает, что цепочка Р выводится из це­почки а за 4 шага вывода¹.

Возьмем в качестве примера ту же грамматику для целых десятичных чисел со знаком G({0.1.2_>3,4,5.6,7,8.9.-.+}.{S.T.F},P,S):

Р:

S -> Т | +Т | -Т Т -> F | TF

F -> 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 Построим в ней несколько произвольных цепочек вывода:

1. S => -Т => -TF => -TFF => -FFF => -4FF => -47F => -479

2. S ==> Т => TF => Т8 => F8 => 18

3. Т => TF => ТО => TF0 => Т50 => F50 => 350

4. TFT => TFFT => TFFF => FFFF => 1FFF => 1FF4 => 10F4 => 1004

5. F=>5

Получили следующие выводы:

1. S => * -479 или S => + -479 или S => 7 -479

2. S => * 18 или S => + 18 или S => 5 18

3. Т => * 350 или Т => + 350 или Т => 6 350

4. TFT => * 1004 или TFT => + 1004 или TFT => 7 1004

5. F => * 5 или F =>' 5 (утверждение F => + 5 неверно!)

Все эти выводы построены на основе грамматики G. В принципе в этой грамма­тике (как, практически, и в любой другой грамматике реального языка) можно построить сколь угодно много цепочек вывода.

Возьмем в качестве второго примера грамматику G₃ ({a,b,c},{B,C,D,S}.P,S) с пра­вилами Р, которая уже рассматривалась выше:

¹ В литературе встречается также обозначение а=>°(3, которое означает, что цепочка а вы­водима из цепочки р за 0 шагов — иными словами, в таком случае эти цепочки равны: а = р. Подразумевается, что обозначение вывода а=>*р допускает и такое толкование — включает в себя вариант а=> р. S -» BD

В -> аВЬС | ab СЬ -> ЬС CD -» Dc bDc -* bcc abD -» abc

Как было сказано ранее, она задает язык L(G₃) = {0ⁿlⁿ | п > 0}. Рассмотрим npi мер вывода предложения «aaaabbbbcccc » языка L(G₃) на основе грамматики G

S => BD => aBbCD => aaBbCbCD => aaaBbCbCbCD => aaaabbCbCbCD => aaaabbbCCbCD = aaaabbbCbCCD => aaaabbbbCCCD => aaaabbbbCCDc => aaaabbbbCDcc => aaaabbbbDccc s aaaabbbbcccc. Тогда для грамматики G₃ получаем вывод: S => * aaaabbbbcccc.

Иногда, чтобы пояснить ход вывода, над стрелкой, обозначающей каждый ш; вывода, пишут обозначение того правила грамматики, на основе которого сдела этот шаг (для этой цели правила грамматики проще всего просто пронумеровать! в порядке их следования). Грамматика, рассмотренная в приведенных здесь npi мерах, содержит всего 15 правил, и на каждом шаге в цепочках вывода можг понять, на основании какого правила сделан этот шаг (читатели могут легко сделать это самостоятельно), но в более сложных случаях пояснения к шагам вывода с указанием номеров правил грамматики могут быть весьма полезными.

Сентенциальная форма грамматики. Язык, заданный грамматикой

Вывод называется законченным, если на основе цепочки р\ полученной в резул: тате вывода, нельзя больше сделать ни одного шага вывода. Иначе говоря, вывс называется законченным, если цепочка р, полученная в результате вывода, пу тая или содержит только терминальные символы грамматики G(VT,VN,P,S PeVT*. Цепочка р, полученная в результате законченного вывода, называете конечной цепочкой вывода.

В рассмотренном выше примере все построенные выводы являются закончеными, а, например, вывод S =>* -4FF (из первой цепочки в примере) будет незако] ченным.

Цепочка символов asV* называется сентенциальной формой грамматики G(V VN,P,S), V = VTuVN, если она выводима из целевого символа грамматики S =>* а. Если цепочка ae VT* получена в результате законченного вывода, то oi называется конечной сентенциальной формой.

Из рассмотренного выше примера можно заключить, что цепочки в символе «—479>> и «18» являются конечными сентенциальными формами грамматики цель Десятичных чисел со знаком, так как существуют выводы S =>* -479 и S =>* 1 (примеры 1 и 2). Цепочка F8 из вывода 2, например, тоже является сентенциальнс формой, поскольку справедливо S =>* F8, но она не является конечной цепочке вывода. В то же время в выводах примеров 3—5 явно не присутствуют сентенц: эльные формы. На самом деле цепочки «350», «1004» и «5» являются конечнг Ми сентенциальными формами. Чтобы доказать это, необходимо просто построить другие цепочки вывода (например, для цепочки «5» строим: S => Т => F => и получаем S => * 5). А вот цепочка «TFT» (пример 4) не выводима из целевого символа грамматики S, а потому сентенциальной формой не является. Язык L, заданный грамматикой G(VT,VN,P,S), — это множество всех конечных сентенциальных форм грамматики G. Язык L, заданный грамматикой G, обозна­чается как L(G). Очевидно, что алфавитом такого языка L(G ) будет множество терминальных символов грамматики VT, поскольку все конечные сентенциаль­ные формы грамматики — это цепочки над алфавитом VT. Следует помнить, что две грамматики G(VT,VN,P,S) и G'(VT',VN',P',S') называ­ются эквивалентными, если эквивалентны заданные ими языки: L(G) = L(G'). Очевидно, что эквивалентные грамматики должны иметь, по крайней мере, пере­секающиеся множества терминальных символов VTnVT * 0 (как правило, эти множества даже совпадают VT = VI"), а вот множества нетерминальных симво­лов, правила грамматики и целевой символ у них могут кардинально отличаться.

Левосторонний и правосторонний выводы

Вывод называется левосторонним, если в нем на каждом шаге вывода правило грамматики применяется всегда к крайнему левому нетерминальному символу в цепочке. Другими словами, вывод называется левосторонним, если на каж­дом шаге вывода происходит подстановка цепочки символов на основании пра­вила грамматики вместо крайнего левого нетерминального символа в исходной цепочке.

Аналогично, вывод называется правосторонним, если в нем на каждом шаге вы­вода правило грамматики применяется всегда к крайнему правому нетерминаль­ному символу в цепочке.

Если рассмотреть цепочки вывода из того же примера, то в нем выводы 1 и 5 яв­ляются левосторонними, выводы 2, 3 и 5 — правосторонними (вывод 5 одновре­менно является и лево- и правосторонним), а вот вывод 4 не является ни лево­сторонним, ни правосторонним.

Для грамматик типов 2 и 3 (КС-грамматик и регулярных грамматик) для любой сентенциальной формы всегда можно построить левосторонний или правосто­ронний выводы. Для грамматик других типов это не всегда возможно, так как по структуре их правил не всегда можно выполнить замену крайнего левого или крайнего правого нетерминального символа в цепочке.

Рассмотренный выше вывод S => * aaaabbbbcccc для грамматики G₃, задающей язык L(G₃) = {Oⁿlⁿ|n > 0}, не является ни левосторонним, ни правосторонним. Грамматика относится к типу 1, и в данном случае для нее нельзя построить та­кой вывод, на каждом шаге которого только один нетерминальный символ заме­нялся бы на цепочку символов.

Дерево вывода. Методы построения дерева вывода

Деревом вывода грамматики G(VT,VN,P,S) называется дерево (граф), которое соответствует некоторой цепочке вывода и удовлетворяет следующим условиям:

• каждая вершина дерева обозначается символом грамматики Ae(VT uVN);

• корнем дерева является вершина, обозначенная целевым символом граммати­ки — S;

• листьями дерева (концевыми вершинами) являются вершины, обозначенные терминальными символами грамматики или символом пустой цепочки X;

• если некоторый узел дерева обозначен символом AeVN, а связанные с ним узлы — символами Ь^.-.^! п > 0, Vn > i > 0: bje(VTuVNu{A.}), то в грамма­тике G(VT,VN,P,S) существует правило А-^Ь^Ьг b_n e Р.

Из определения видно, что по структуре правил дерево вывода в указанном виде всегда можно построить только для грамматик типов 2 и 3 (контекстно-свобод­ных и регулярных). Для грамматик других типов дерево вывода в таком виде можно построить не всегда (либо же оно будет иметь несколько иной вид).

На основе рассмотренного выше примера построим деревья вывода для цепочек вывода 1 и 2. Эти деревья приведены на рис. 9.2.

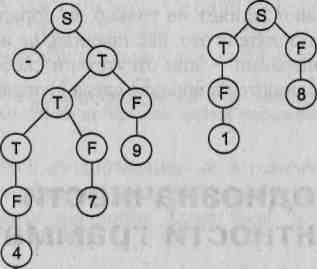
Рис. 9.2. Примеры деревьев вывода для грамматики целых десятичных чисел со знаком

Для того чтобы построить дерево вывода, достаточно иметь только цепочку вывода. Дерево вывода можно построить двумя способами: сверху вниз и снизу вверх. Для строго формализованного построения дерева вывода всегда удобнее пользоваться строго определенным выводом: либо левосторонним, либо право­сторонним.

При построении дерева вывода сверху вниз построение начинается с целевого символа грамматики, который помещается в корень дерева. Затем в грамматике выбирается необходимое правило, и на первом шаге вывода корневой символ раскрывается на несколько символов первого уровня. На втором шаге среди всех концевых вершин дерева выбирается крайняя (крайняя левая — для левосторон­него вывода, крайняя правая — для правостороннего) вершина, обозначенная нетерминальным символом, для этой вершины выбирается нужное правило грамматики, и она раскрывается на несколько вершин следующего уровня. По­строение дерева заканчивается, когда все концевые вершины обозначены терми­нальными символами, в противном случае надо вернуться ко второму шагу и продолжить построение.

Построение дерева вывода снизу вверх начинается с листьев дерева. В качестве листьев выбираются терминальные символы конечной цепочки вывода, которые на первом шаге построения образуют последний уровень (слой) дерева. Построе­ние дерева идет по слоям. На втором шаге построения в грамматике выбирается правило, правая часть которого соответствует крайним символам в слое дерева (крайним правым символам при правостороннем выводе и крайним левым — при левостороннем). Выбранные вершины слоя соединяются с новой вершиной, которая выбирается из левой части правила. Новая вершина попадает в слой де­рева вместо выбранных вершин. Построение дерева закончено, если достигнута корневая вершина (обозначенная целевым символом), а иначе надо вернуться ко второму шагу и повторить его над полученным слоем дерева. Поскольку все известные языки программирования имеют нотацию записи «сле­ва — направо», компилятор также всегда читает входную программу слева на­право (и сверху вниз, если программа разбита на несколько строк). Поэтому для построения дерева вывода методом «сверху вниз», как правило, используется ле­восторонний вывод, а для построения «снизу вверх» — правосторонний вывод. На эту особенность компиляторов стоит обратить внимание. Нотация чтения программ «слева направо» влияет не только на порядок разбора программы компилятором (для пользователя это, как правило, не имеет значения), но и на порядок выполнения операций — при отсутствии скобок большинство равно­правных операций выполняются в порядке слева направо, а это уже имеет суще­ственное значение.

Проблемы однозначности

и эквивалентности грамматик

Однозначные и неоднозначные грамматики

Рассмотрим некоторую грамматику G ({+,-.*,/,(,). а, b}, {S}, Р, S):

Р: S -> S+S | S-S | S*S | S/S | (S) | а | b Видно, что представленная грамматика определяет язык арифметических выра­жений с четырьмя основными операциями (сложение, вычитание, умножение и деление) и скобками над операндами а и Ь. Примерами предложений этого язы­ка могут служить: a*b+a, a*(a+b), а*Ь+а*а и т. д.

Возьмем цепочку а*Ь+а и построим для нее левосторонний вывод. Получится два варианта:

S => S+S => S*S+S о a*S+S => a*b+S => a*b+a S => S*S => a*S => a*S+S => a*b+S => a*b+a Каждому из этих вариантов будет соответствовать свое дерево вывода. Два вари­анта дерева вывода для цепочки «а*Ь+а» приведены на рис. 9.3. С точки зрения формального языка, заданного грамматикой, не имеет значения, какая цепочка вывода и какое дерево вывода из возможных вариантов будут построены. Однако для языков программирования, которые не являются чисто

формальными языками и несут некоторую смысловую нагрузку, это имеет зна­чение. Например, если принять во внимание, что рассмотренная здесь граммати­ка определяет язык неких арифметических выражений, то с точки зрения ариф­метики порядок построения дерева вывода соответствует порядку выполнения арифметических действий. В арифметике, как известно, при отсутствии скобок умножение всегда выполняется раньше сложения (умножение имеет более высо­кий приоритет), но в рассмотренной выше грамматике это ниоткуда не следу­ет—в ней все операции равноправны. Поэтому с точки зрения арифметических операций приведенная грамматика имеет неверную семантику — в ней нет при­оритета операций, а, кроме того, для равноправных операций не определен поря­док выполнения («слева направо»), хотя синтаксическая структура построенных с ее помощью выражений будет правильной.

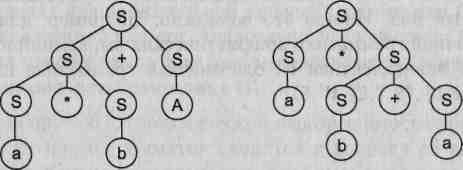
Рис. 9.3. Два варианта дерева цепочки «а*Ь+а» вывода для неоднозначной грамматики арифметических выражений

Такая ситуация называется неоднозначностью в грамматике. Естественно, для построения компиляторов и языков программирования нельзя использовать грам­матики, допускающие неоднозначности. Дадим более точное определение неод­нозначной грамматики.

Грамматика называется однозначной, если для каждой цепочки символов языка, заданного этой грамматикой, можно построить единственный левосторонний (и единственный правосторонний) вывод. Или, что то же самое: грамматика называется однозначной, если для каждой цепочки символов языка, заданного этой грамматикой, существует единственное дерево вывода. В противном случае грамматика называется неоднозначной.

Рассмотренная в примере грамматика арифметических выражений, очевидно, является неоднозначной.

Эквивалентность и преобразование грамматик

Поскольку грамматика языка программирования, по сути, всегда должна быть однозначной, то возникают два вопроса, которые необходимо в любом случае ре­шить:

Q как проверить, является ли данная грамматика однозначной? □ если заданная грамматика является неоднозначной, то как преобразовать ее к однозначному виду?

Однозначность — это свойство грамматики, а не языка. Для некоторых языков, заданных неоднозначными грамматиками, иногда удается построить эквивалент­ную однозначную грамматику (однозначную грамматику, задающую тот же язык).

Чтобы убедиться в том, что некоторая грамматика не является однозначной (яв­ляется неоднозначной), согласно определению достаточно найти в заданном ею языке хотя бы одну цепочку, которая бы допускала более чем один левосторон­ний или правосторонний вывод (как это было в рассмотренном примере). Одна­ко не всегда удается легко обнаружить такую цепочку символов. Кроме того, если такая цепочка не найдена, мы не можем утверждать, что данная грамматика является однозначной, поскольку перебрать все цепочки языка невозможно -как правило, их бесконечное количество. Следовательно, нужны другие способы проверки однозначности грамматики.

Если грамматика все же является неоднозначной, то необходимо преобразовать ее в однозначный вид. Иногда это возможно. Например, для рассмотренной выше неоднозначной грамматики арифметических выражений над операциями а и b существует эквивалентная ей однозначная грамматика следующего вида G'({+,-.*,/,(.),a,b}.{S,T,E},P\S):

Р':

S _> S+T | S-T | Т

Т -> Т*Е | Т/Е | Е

Е -> (S) | а | b В этой грамматике для рассмотренной выше цепочки символов языка а*Ь+а воз­можен только один левосторонний вывод:

S => S+T => Т+Т => Т*Е+Т Ь Е*Е+Т =* а*Е+Т => а*Ь+Т => a*b+E => a*b+a Этому выводу соответствует единственно возможное дерево вывода. Оно приве­дено на рис. 9.4. Видно, что хотя цепочка вывода несколько удлинилась, но при­оритет операций в данном случае единственно возможный и соответствует их порядку в арифметике.

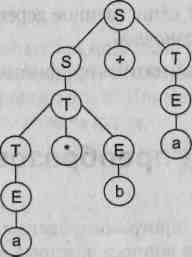
Рис. 9.4. Дерево вывода для однозначной грамматики арифметических выражений

В таком случае необходимо решить две проблемы: во-первых, доказать, что две имеющиеся грамматики эквивалентны (задают один и тот же язык); во-вторых, иметь возможность проверить, что вновь построенная грамматика является од­нозначной.

Проблема эквивалентности грамматик в общем виде формулируется следующим образом: имеются две грамматики G и G', необходимо построить алгоритм, кото­рый бы позволял проверить, являются ли эти две грамматики эквивалентными.

К сожалению, доказано, что проблема эквивалентности грамматик в общем слу­чае алгоритмически неразрешима. Это значит, что не только до сих пор не суще­ствует алгоритма, который бы позволял проверить, являются ли две заданные грамматики эквивалентными, но и доказано, что такой алгоритм в принципе не существует, а значит, он никогда не будет создан.

Точно так же неразрешима в общем виде и проблема однозначности грамматик. Это значит, что не существует (и никогда не будет существовать) алгоритм, который бы позволял для произвольной заданной грамматики G проверить, яв­ляется ли она однозначной или нет. Аналогично, не существует алгоритма, кото­рый бы позволял преобразовать заведомо неоднозначную грамматику G в экви­валентную ей однозначную грамматику G'.

В общем случае вопрос об алгоритмической неразрешимости проблем однознач­ ности и эквивалентности грамматик сводится к вопросу об алгоритмической неразрешимости проблемы, известной как «проблема соответствий Поста». Про­ блема соответствий Поста формулируется следующим образом: имеется задан­ ное множество пар непустых цепочек над алфавитом V: {(ctj,Pi)> (а₂,р₂) (^ап>Рп)}>

п > 0, Vn > i > 0: oippieV*; необходимо проверить, существует ли среди них такая последовательность пар цепочек: (cq.Pi), (a₂,P2),..., (a_m,p_m), m > 0 (необязательно различных), что a^.-.a,,, = p₁p₂...p_rn- Доказано, что не существует алгоритма, ко­торый бы за конечное число шагов мог дать ответ на этот вопрос, хотя на первый взгляд постановка задачи кажется совсем несложной.

То, что проблема не решается в общем виде, совсем не значит, что ее нельзя ре­шить в каждом конкретном случае. Например, для алфавита V - {а,Ь} можно по­строить множество пар цепочек {(abbb.b). (a.aab), (ba.b)} и найти одно из реше­ний: (a,aab),(a,aab),(ba,b),(abbb,b) - видно, что (a)(a)(ba)(abbb) = (aabKaab) (b)(b). А для множества пар цепочек {(ab,aba),(aba,baa),(baa,aa)} очевидно, что решения не существует.

Точно так же неразрешимость проблем эквивалентности и однозначности грам­матик в общем случае совсем не означает, что они не разрешимы вообще. Для не­которых частных случаев — например, для определенных типов и классов грам­матик (в частности, для регулярных грамматик) — эти проблемы решены. Также их иногда удается решить полностью или частично в каждом конкретном случае, и для конкретной заданной грамматики доказать, является ли она однозначной или нет. Например, приведенная выше грамматика G' для арифметических вы­ражений над операндами а и b относится к классу грамматик операторного пред­шествования из типа КС-грамматик. На основе этой грамматики возможно по­строить распознаватель в виде детерминированного расширенного МП-автомата, а потому можно утверждать, что она является однозначной (см. раздел «Восхо­дящие распознаватели КС-языков без возвратов», глава 12).

Правила, задающие неоднозначность в грамматиках

В общем виде невозможно проверить, является ли заданная грамматика одно­значной или нет. Однако для КС-грамматик существуют определенного вида правила, по наличию которых в множестве правил грамматики G(VT,VN,P,S) можно утверждать, что она является неоднозначной. Эти правила имеют сле­дующий вид:

1. А -» АА | а,

2. А -» АаА | (3,

3. А -> аА | Ар | у,

4. А -> аА | аАрА | у,

здесь AeVN; a,p,ye(VNuVT)*. Если в заданной грамматике встречается хотя бы одно правило подобного вида (любого из приведенных вариантов), то доказано, что такая грамматика точно будет неоднозначной. Однако если подобных правил во всем множестве правил грамматики нет, это совсем не означает, что грамматика является однозначной. Такая грамматика может быть однозначной, а может и не быть. То есть отсутст­вие правил указанного вида (всех вариантов) — это необходимое, но не достаточ­ное условие однозначности грамматики.

С другой стороны, установлены условия, при удовлетворении которым грамма­тика заведомо является однозначной. Они справедливы для всех регулярных и многих классов контекстно-свободных грамматик. Однако известно, что эти ус­ловия, напротив, являются достаточными, но не необходимыми для однозначно­сти грамматик.

В рассмотренном выше примере грамматики арифметических выражений с опе­рандами а и b — G({+,-,*,/,(.),а,b},{S},P,S) — во множестве правил Р: S -> S+S | S-S | S*S | S/S | (S) | а | b встречаются правила 2 типа. Поэтому данная грам­матика является неоднозначной, что и было показано выше.

Распознаватели. Задача разбора

Общая схема распознавателя

Для каждого языка программирования (как, наверное, и для многих других язы­ков) важно не только уметь построить текст програмы на этом языке, но и оп­ределить принадлежность имеющегося текста к данному языку. Именно эту задачу решают компиляторы в числе прочих задач (компилятор должен не толь­ко распознать исходную программу, но и построить эквивалентную ей результи­рующую программу). В отношении исходной программы компилятор выступает как распознаватель, а человек, создавший программу на некотором языке, высту­пает в роли генератора цепочек этого языка.

Распознаватель (или разборщик) — это специальный алгоритм, который позво­ляет определить принадлежность цепочки символов некоторому языку. Задача распознавателя заключается в том, чтобы на основании исходной цепочки дать ответ, принадлежит ли она заданному языку или нет. Распознаватели, как было сказано выше, представляют собой один из способов определения языка.

В общем виде распознаватель можно отобразить в виде условной схемы, пред­ставленной на рис. 9.5.

дом шаге работы распознавателя считывающая головка может либо переместить­ся по ленте символов на некоторое число позиций в заданном направлении, либо остаться на месте. Поскольку все языки программирования подразумевают нота­цию чтения исходной программы «слева направо», то так же работают и все рас­познаватели. Поэтому, когда говорят об односторонних распознавателях, то пре­жде всего имеют в виду левосторонние, которые читают исходную цепочку слева направо и не возвращаются назад к уже прочитанной части цепочки.

Двусторонние распознаватели допускают, что считывающая головка может пе­ремещаться относительно ленты входных символов в обоих направлениях: как вперед, от начала ленты к концу, так и назад, возвращаясь к уже прочитанным символам.

По видам устройства управления распознаватели бывают детерминированные и недетерминированные.

Распознаватель называется детерминированным в том случае, если для каждой допустимой конфигурации распознавателя, которая возникла на некотором шаге его работы, существует единственно возможная конфигурация, в которую распо­знаватель перейдет на следующем шаге работы.

В противном случае распознаватель называется недетерминированным. Неде­терминированный распознаватель может иметь такую допустимую конфигу­рацию, для которой существует некоторое конечное множество конфигураций, возможных на следующем шаге работы. Достаточно иметь хотя бы одну такую конфигурацию, чтобы распознаватель был недетерминированным.

По видам внешней памяти распознаватели бывают следующих типов:

• распознаватели без внешней памяти;

• распознаватели с ограниченной внешней памятью;

• распознаватели с неограниченной внешней памятью.

У распознавателей без внешней памяти эта память полностью отсутствует. В про­цессе их работы используется только конечная память устройства управления, доступ к внешней памяти не выполняется.

Для распознавателей с ограниченной внешней памятью размер внешней памяти ограничен в зависимости от длины исходной цепочки символов. Эти ограниче­ния могут налагаться некоторой зависимостью объема памяти от длины цепоч­ки — линейной, полиномиальной, экспоненциальной и т. д. Кроме того, для та­ких распознавателей может быть указан способ организации внешней памяти — стек, очередь, список и т. п.

Распознаватели с неограниченной внешней памятью предполагают, что для их работы может потребоваться внешняя память неограниченного объема (как пра­вило, вне зависимости от длины входной цепочки). У таких распознавателей предполагается память с произвольным методом доступа.

Вместе эти три составляющих позволяют организовать общую классификацию распознавателей. Например, в этой классификации возможен такой тип: «дву­сторонний недетерминированный распознаватель с линейно ограниченной сте­ковой памятью».

Тип распознавателя в классификации определяет сложность создания такого распознавателя, а следовательно, сложность разработки соответствующего про­граммного обеспечения для компилятора. Чем выше в классификации стоит рас­познаватель, тем сложнее создавать алгоритм, обеспечивающий его работу. Раз­рабатывать двусторонние распознаватели сложнее, чем односторонние. Можно заметить, что недетерминированные распознаватели по сложности выше детер­минированных. Зависимость затрат на создание алгоритма от типа внешней па­мяти также очевидна.

Классификация распознавателей по типам языков

Как было показано в предыдущей главе, классификация распознавателей (вид входящих в состав распознавателя компонентов) определяет сложность алгорит­ма работы распознавателя. Но сложность распознавателя также напрямую связа­на с типом языка, входные цепочки которого может принимать (допускать) рас­познаватель.

Выше было определено четыре основных типа языков. Доказано, что для каждого из этих типов языков существует свой тип распознавателя с определенным со­ставом компонентов и, следовательно, с заданной сложностью алгоритма работы. Для языков с фразовой структурой (тип 0) Необходим распознаватель, равномощной машине Тьюринга — недетерминированный двусторонний автомат, имею­щий неограниченную внешнюю память. Поэтому для языков данного типа нель­зя гарантировать, что за ограниченное время на ограниченных вычислительных ресурсах распознаватель завершит работу и примет решение о том, принадлежит или не принадлежит входная цепочка заданному языку. Отсюда можно заклю­чить, что практического применения языки с фразовой структурой не имеют (и не будут иметь), а потому далее они не рассматриваются. Для контекстно-зависимых языков (тип 1) распознавателями являются двусто­ронние недетерминированные автоматы с линейно ограниченной внешней памя­тью. Алгоритм работы такого автомата в общем случае имеет экспоненциальную сложность — количество шагов (тактов), необходимых автомату для распознава­ния входной цепочки, экспоненциально зависит от длины этой цепочки. Следо­вательно, и время, необходимое на разбор входной цепочки по заданному алго­ритму, экспоненциально зависит от длины входной цепочки символов. Такой алгоритм распознавателя уже может быть реализован в программном обес­печении компьютера — зная длину входной цепочки, всегда можно сказать, за какое максимально возможное время будет принято решение о принадлежности цепочки данному языку и какие вычислительные ресурсы для этого потребуют­ся. Однако экспоненциальная зависимость времени разбора от длины цепочки существенно ограничивает применение распознавателей для контекстно-зависи­мых языков. Как правило, такие распознаватели применяются для автоматизи­рованного перевода и анализа текстов на естественных языках, когда временные ограничения на разбор текста несущественны (следует также напомнить, что, по­скольку естественные языки более сложны, чем контекстно-зависимый тип, то после такой обработки часто требуется вмешательство человека). В компилято-

Входная цепочка символов |ai|a₂| |a_n|

+ Считывающая головка

УУ К-

Рабочая

(внешняя)

память

Рис. 9.5. Условная схема распознавателя

Следует подчеркнуть, что представленный рисунок — всего лишь условная схе­ма, отображающая работу алгоритма распознавателя. Ни в коем случае не стоит искать подобного устройства в составе компьютера. Распознаватель, являющийся частью компилятора, представляет собой часть программного обеспечения ком­пьютера.

Как видно из рисунка, распознаватель состоит из следующих основных компо­нентов:

• ленты, содержащей исходную цепочку входных символов, и считывающей го­ловки, обозревающей очередной символ в этой цепочке;

• устройства управления (УУ), которое координирует работу распознавателя, имеет некоторый набор состояний и конечную память (для хранения своего состояния и некоторой промежуточной информации);

• внешней (рабочей) памяти, которая может хранить некоторую информацию в процессе работы распознавателя и в отличие от памяти УУ может иметь не­ограниченный объем.

Распознаватель работает с символами своего алфавита — алфавита распознава­теля. Алфавит распознавателя конечен. Он включает в себя все допустимые сим­волы входных цепочек, а также некоторый дополнительный алфавит символов, которые могут обрабатываться УУ и храниться в рабочей памяти распознава­теля.

В процессе своей работы распознаватель может выполнять некоторые элемен­тарные операции, такие как чтение очередного символа из входной цепочки, сдвиг входной цепочки на заданное количество символов (вправо или влево), доступ к рабочей памяти для чтения или записи информации, преобразование информации в памяти, изменение состояния УУ. То, какие конкретно операции должны выполняться в процессе работы распознавателя, определяется в УУ.

Распознаватель работает по шагам или тактам. В начале такта, как правило, счи-тывается очередной символ из входной цепочки, и в зависимости от этого симво­ла УУ определяет, какие действия необходимо выполнить. Вся работа распозна­вателя состоит из последовательности тактов. В начале каждого такта состояние распознавателя определяется его конфигурацией. В процессе работы конфигура­ция распознавателя меняется. Конфигурация распознавателя определяется следующими параметрами:

• содержимое входной цепочки символов и положение считывающей головки в ней;

• состояние УУ;

• содержимое внешней памяти.

Для распознавателя всегда задается определенная конфигурация, которая счи­тается начальной конфигурацией. В начальной конфигурации считывающая головка обозревает первый символ входной цепочки, УУ находится в заданном начальном состоянии, а внешняя память либо пуста, либо содержит строго опре­деленную информацию.

Кроме начального состояния для распознавателя задается одна или несколько конечных конфигураций. В конечной конфигурации считывающая головка, как правило, находится за концом исходной цепочки (часто для распознавателей вводят специальный символ, обозначающий конец входной цепочки). Распознаватель допускает входную цепочку символов а, если, находясь в началь­ной конфигурации и получив на вход эту цепочку, он может проделать последо­вательность шагов, заканчивающуюся одной из его конечных конфигураций. Формулировка «может проделать последовательность шагов» более точна, чем прямое указание «проделает последовательность шагов», так как для многих распознавателей при одной и той же входной цепочке символов из начальной конфигурации могут быть допустимы различные последовательности шагов, не все из которых ведут к конечной конфигурации.

Язык, определяемый распознавателем, — это множество всех цепочек, которые допускает распознаватель.

Далее в главах этого пособия рассмотрены конкретные типы распознавателей для различных типов языков. Но все, что было сказано здесь, относится ко всем без исключения типам распознавателей для всех типов языков.

Виды распознавателей

Распознаватели можно классифицировать в зависимости от вида составляющих их компонентов: считывающего устройства, устройства управления (УУ) и внеш­ней памяти.

По видам считывающего устройства распознаватели могут быть двусторонние и односторонние.

Односторонние распознаватели допускают перемещение считывающей головки по ленте входных символов только в одном направлении. Это значит, что на каж-

рах для анализа текстов на различных языках программирования контекстно-за­висимые распознаватели не применяются, поскольку скорость работы компиля­тора имеет существенное значение, а синтаксический разбор текста программы можно выполнять в рамках более простого, контекстно-свободного типа языков.

Поэтому в рамках этого учебного пособия контекстно-зависимые языки также не рассматриваются.

Для контекстно-свободных языков (тип 2) распознавателями являются односто­ронние недетерминированные автоматы с магазинной (стековой) внешней па­мятью — МП-автоматы. При простейшей реализации алгоритма работы такого автомата он имеет экспоненциальную сложность, однако путем некоторых усо­вершенствований алгоритма можно добиться полиномиальной (кубической) за­висимости времени, необходимого на разбор входной цепочки, от длины этой цепочки. Следовательно, можно говорить о полиномиальной сложности распо­знавателя для КС-языков.

Среди всех КС-языков можно выделить класс детерминированных КС-языков, распознавателями для которых являются детерминированные автоматы с мага­зинной (стековой) внешней памятью — ДМП-автоматы. Эти языки обладают свойством однозначности — доказано, что для любого детерминированного КС-языка всегда можно построить однозначную грамматику. Кроме того, для таких языков существует алгоритм работы распознавателя с квадратичной сложно­стью. Поскольку эти языки являются однозначными, именно они представляют наибольший интерес для построения компиляторов.

Более того, среди всех детерминированных КС-языков существуют такие классы языков, для которых возможно построить линейный распознаватель — распозна­ватель, у которого время принятия решения о принадлежности цепочки языку имеет линейную зависимость от длины цепочки. Синтаксические конструкции практически всех существующих языков программирования могут быть отнесе­ны к одному из таких классов языков. Это обстоятельство очень важно для раз­работки современных быстродействующих компиляторов. Поэтому в главе, по­священной КС-языкам, в первую очередь будет уделено внимание именно таким классам этих языков.

Тем не менее следует помнить, что только синтаксические конструкции языков программирования допускают разбор с помощью распознавателей КС-языков. Сами языки программирования, как уже было сказано, не могут быть полностью отнесены к типу КС-языков, поскольку предполагают некоторую контекстную зависимость в тексте исходной программы (например, такую, как необходимость предварительного описания переменных). Поэтому кроме синтаксического раз­бора практически все компиляторы предполагают дополнительный семантиче­ский анализ текста исходной программы. Этого можно было бы избежать, если построить компилятор на основе контекстно-зависимого распознавателя, но ско­рость работы такого компилятора была бы недопустима низка, поскольку время разбора в таком варианте будет экспоненциально зависеть от длины исходной программы. Комбинация из распознавателя КС-языка и дополнительного семан­тического анализатора является более эффективной с точки зрения скорости разбора исходной программы. Для регулярных языков (тип 3) распознавателями являются односторонние неде­терминированные автоматы без внешней памяти — конечные автоматы (KA'i Это очень простой тип распознавателя, который всегда предполагает линейную зависимость времени на разбор входной цепочки от ее длины. Кроме того, конеч­ные автоматы имеют важную особенность: любой недетерминированный КА всегда может быть преобразован в детерминированный. Это обстоятельство су­щественно упрощает разработку программного обеспечения, обеспечивающего функционирование распознавателя.

Простота и высокая скорость работы распознавателей определяют широкую об­ласть применения регулярных языков.

В компиляторах распознаватели на основе регулярных языков используются для лексического анализа текста исходной программы — выделения в нем про­стейших конструкций языка, таких как идентификаторы, строки, константы и т. п. Это позволяет существенно сократить объем исходной информации и упрощает синтаксический разбор программы. Более подробно взаимодействие лексическо­го и синтаксического анализаторов текста программы рассмотрено дальше, в гла­ве, посвященной структуре компилятора. На основе распознавателей регулярных языков функционируют ассемблеры — компиляторы с языков ассемблера (мне­мокода) в язык машинных команд.

Кроме компиляторов регулярные языки находят применение еще во многих областях, связанных с разработкой программного обеспечения вычислительных систем. На их основе функционируют многие командные процесоры как в сис­темном, так и в прикладном программном обеспечении. Для регулярных языков существуют развитые, математически обоснованные механизмы, которые позво­ляют облегчить создание распознавателей. Они положены в основу существую­щих разнообразных программных средств, которые позволяют автоматизировать этот процесс.

Регулярные языки и связанные с ними математические методы рассматриваются в отдельной главе данного учебного пособия.

Задача разбора (постановка задачи)

Грамматики и распознаватели — два независимых метода, которые реально мо­гут быть использованы для определения какого-либо языка. Однако при разра­ботке компилятора для некоторого языка программирования возникает задача, которая требует связать между собой эти методы задания языков. Разработчики компилятора всегда имеют дело с уже определенным языком про­граммирования. Грамматика для синтаксических конструкций этого языка из­вестна. Она, как правило, четко описана в стандарте языка, и хотя форма опи­сания может быть произвольной, ее всегда можно преобразовать к требуемому виду (например, к форме Бэкуса—Наура или к форме описания с использованием метасимволов). Задача разработчиков заключается в том, чтобы построить рас­познаватель для заданного языка, который затем будет основой синтаксического анализатора в компиляторе.

Таким образом, задача разбора в общем виде заключается в следующем: на осно­ве имеющейся грамматики некоторого языка построить распознаватель для этого языка. Заданная грамматика и распознаватель должны быть эквивалентны, то есть определять один и тот же язык (часто допускается, чтобы они были почти эквивалентны, поскольку пустая цепочка во внимание обычно не принимается).

Задача разбора в общем виде может быть решена не для всех типов языков. Но как было сказано выше, разработчиков компиляторов интересуют, прежде всего, контекстно-свободные и регулярные языки. Для данных типов языков доказано, что задача разбора для них разрешима. Более того, для них найдены формальные методы ее решения. Описанию и обоснованию именно методов решения задачи разбора и будет посвящена большая часть материала последующих глав.

Поскольку языки программирования не являются чисто формальными языками и несут в себе некоторый смысл (семантику), то задача разбора для создания ре­альных компиляторов понимается несколько шире, чем она формулируется для чисто формальных языков. Компилятор должен не просто дать ответ, принадле­жит или нет входная цепочка символов заданному языку, но и определить ее смысловую нагрузку. Для этого необходимо выявить те правила грамматики, на основании которых цепочка была построена. Фактически работа распознавате­лей в составе компиляторов сводится к построению в том или ином виде дерева разбора входной цепочки. Затем уже это дерево разбора используется компиля­тором для синтеза результирующего кода.

Кроме того, если входная цепочка символов не принадлежит заданному языку — исходная программа содержит ошибку, — разработчику программы не интересно просто узнать сам факт наличия ошибки. В данном случае задача разбора также расширяется: распознаватель в составе компилятора должен не только устано­вить факт присутствия ошибки во входной программе, но и по возможности оп­ределить тип ошибки и то место в цепочке символов, где она встречается.

Регулярные языки и грамматики

Леволинейные и праволинейные грамматики. Автоматные грамматики

К регулярным, как уже было сказано, относятся два типа грамматик: леволинейные и праволинейные.

Леволинейные грамматики G(VT,VN,P,S), V = VNuVT могут иметь правила дву видов: А-»Ву или А-»у, где A,BeVN, yeVT*.

В свою очередь, праволинейные грамматики G(VT,VN,P,S), V - VNuVT могу иметь правила также двух видов: А-»уВ или А-»у, где A.BeVN, yeVT*.

Доказано, что эти два класса грамматик эквивалентны. Для любого регулярног языка, заданного праволинейной грамматикой, может быть построена левол* нейная грамматика, определяющая эквивалентный язык; и наоборот — для лк бого регулярного языка, заданного леволинейной грамматикой, может быть ш строена праволинейная грамматика, задающая эквивалентный язык.

Разница между леволинейными и праволинейными грамматиками заключаете в основном в том, в каком порядке строятся предложения языка: слева направления для леволинейных либо справа налево для праволинейных. Поскольку предл< жения языков программирования строятся, как правило, в порядке слева направления; то в дальнейшем в разделе регулярных грамматик будет идти речь в перву очередь о леволинейных грамматиках.

Среди всех регулярных грамматик можно выделить отдельный класс — автома ные грамматики. Они также могут быть леволинейными и праволинейными.

Леволинейные автоматные грамматики G(VT,VN,P,S), V - VNuVT могут имс правила двух видов: A-»Bt или A-»t, где A.BeVN, teVT.

Праволинейные автоматные грамматики G(VT,VN,P,S), V - VNuVT могут име правила двух видов: A-»tB или A-»t, где A.BeVN, teVT.

Разница между автоматными грамматиками и обычными регулярными rpai матиками заключается в следующем: там, где в правилах обычных регулярньграмматик может присутствовать цепочка терминальных символов, в автомат­ных грамматиках может присутствовать только один терминальный символ. Лю­бая автоматная грамматика является регулярной, но не наоборот — не всякая регулярная грамматика является автоматной.

Доказано, что классы обычных регулярных грамматик и автоматных грамматик почти эквивалентны. Это значит, что для любого языка, который задан регу­лярной грамматикой, можно построить автоматную грамматику, определяющую почти эквивалентный язык (обратное утверждение очевидно).

Чтобы классы автоматных и регулярных грамматик были полностью эквивалент­ны, в автоматных грамматиках разрешается дополнительное правило вида S->^., где S — целевой символ грамматики. При этом символ S не должен встречаться в правых частях других правил грамматики. Тогда язык, заданный автоматной грамматикой G может включать в себя пустую цепочку: >.eL(G). В таком случае автоматные леволинейные и праволинейные грамматики, так же как обычные леволинейные и праволинейные грамматики, задают регулярные языки. Поскольку реально используемые языки, как правило не содержат пустую цепочку симво­лов, разница на пустую цепочку между этими двумя типами грамматик значения не имеет и правила вида S->X далее рассматриваться не будут.

Существует алгоритм, который позволяет преобразовать произвольную регуляр­ную грамматику к автоматному виду — то есть построить эквивалентную ей ав­томатную грамматику. Этот алгоритм рассмотрен ниже. Он является исклю­чительно полезным, поскольку позволяет существенно облегчить построение распознавателей для регулярных грамматик.

Алгоритм преобразования регулярной грамматики к автоматному виду

Имеется регулярная грамматика G(VT,VN,P,S), необходимо преобразовать ее в почти эквивалентную автоматную грамматику G'(VT,VN',P',S'). Для опреде­ленности будем рассматривать леволинейные грамматики, как уже было сказано выше (для праволинейных грамматик можно легко построить аналогичный ал­горитм).

Алгоритм преобразования прост и заключается он в следующей последователь­ности действий:

Шаг 1. Все нетерминальные символы из множества VN грамматики G перено­сятся во множество VN' грамматики G'.

Шаг 2. Необходимо просматривать все множество правил Р грамматики G.

Если встречаются правила вида А->Ва!, A.BeVN, a_teVT или вида А-^, AeVN, aieVT, то они переносятся во множество Р' правил грамматики G' без измене­ний.

Если встречаются правила вида A->Baia₂...a„, n> 1, A,BeVN, Vn>i>0: а^УТ, то во множество нетерминальных символов VN' грамматики G' добавляются

символы Ai,A₂ А_п__ь а во множество правил Р' грамматики G' добавляются

правила:

A—> A_n_!a_n A_n-i-> A_n_₂a_n_i

A₂—> Aja₂ A^Ba!

Если встречаются правила вида A-^a^.-.a,,, n > 1, AeVN, Vn > i > 0: а_;еVT, то во множество нетерминальных символов VN' грамматики G' добавляются символы AtA^-A,,-!, а во множество правил Р' грамматики G' добавляются правила:

А—> А_п_!а_п An-i^-* An.^n-j

А₂-> А,а₂

Если встречаются правила вида А-»В или вида А->Х., то они переносятся во мно­жество правил Р' грамматики G' без изменений.

Шаг 3. Просматривается множество правил Р' грамматики G'. В нем ищутся пра­вила вида А->В или вида А-»А,.

Если находится правило вида А->В, то просматривается множество правил Р' грамматики G'. Если в нем присутствует правила вида В-»С, В->Са, В-»а или В-»Х,, то в него добавляются правила вида А-»С, А->Са, А->а и А->Х соответст­венно, VA,B,CeVN\ VaeVT' (при этом следует учитывать, что в грамматике не должно быть совпадающих правил, и если какое-то правило уже присутствует в грамматике G', то повторно его туда добавлять не следует). Правило А->В уда­ляется из множества правил Р'.

Если находится правило вида А->\, то просматривается множество правил Р' грамматики G'. Если в нем присутствует правило вида В->А или В->Аа, то в него добавляются правила вида В-»А, и В-»а соответственно, VA.BeVN', VaeVT' (при этом следует учитывать, что в грамматике не должно быть совпадающих правил, и если какое-то правило уже присутствует в грамматике G', то повторно его туда добавлять не следует). Правило А-»Х, удаляется из множества правил Р'. Шаг 4. Если на шаге 3 было найдено хотя бы одно правило вида А->В или А-»Х во множестве правил Р' грамматики G', то надо повторить шаг 3, иначе перейти к шагу 5.

Шаг 5. Целевым символом S' грамматики G' становится символ S. Шаги 3 и 4 алгоритма в принципе можно не выполнять, если грамматика не со­держит правил вида А-»В (такие правила называются цепными) или вида А-»> (такие правила называются ^-правилами). Реальные регулярные грамматики обыч­но не содержат правил такого вида. Тогда алгоритм преобразования грамматик* к автоматному виду существенно упрощается. Кроме того, эти правила можн( было бы устранить предварительно с помощью специальных алгоритмов преоб разования (они рассмотрены дальше, в главе, посвященной КС-грамматикам, не также применимы и к регулярным грамматикам).

Пример преобразования регулярной грамматики к автоматному виду

Рассмотрим в качестве примера следующую простейшую регулярную граммати­ку: G({"a". "(","*",")","{"."}"}. {S.CK}, Р, 5)(символыа. (, *, ), {, } из мно­жества терминальных символов грамматики взяты в кавычки, чтобы выделить их среди фигурных скобок, обозначающих само множество):

Р:

S -> С*) | К}

С -* (* | Са | С{ | С} | С( | С* | С)

К -► { | Ка | К( | К* | К) | К{

Если предположить, что а здесь — это любой алфавитно-цифровой символ, кро­ме символов (, *. ), {, }, то эта грамматика описывает два типа комментариев, допустимых в языке программирования Borland Pascal. Преобразуем ее в авто­матный вид.

Шаг 1. Построим множество VN' = {S,C,K}.

Шаг 2. Начинаем просматривать множество правил Р грамматики G.

Для правила S ->• С*) во множество VN' включаем символ Si, а само правило разбиваем на два: S -> S_t) и Si -» С*; включаем эти правила во множество пра­вил Р'.

Правило S -» К} переносим во множество правил Р' без изменений.

Для правила С -> (* во множество VN' включаем символ С_ь а само правило раз­биваем на два: С -> C_t* и С! -> (; включаем эти два правила во множество пра­вил Р'.

Правила С -» Са | С{ | С} | С( | С* | С) переносим во множество правил Р' без изменений.

Правила К -» { | Ка | К( | К* | К) | К{ переносим во множество правил Р' без из­менений.

Шаг 3. Правил вида А->В или А-»Х, во множестве правил Р' не содержится.

Шаг 4. Переходим к шагу 5.

Шаг 5. Целевым символом грамматики G' становится символ S.

В итоге получаем автоматную грамматику:

G'({"a"."("."*".")"."{"."}"}■ {_{S S[ c Ci|K}^ _р._ _S).

Р':

$% ЭД | К}

S, -+ с*

С -> d* | Са | С{ | С} | С( | С* | С)

t, -> (

К -» { | Ка | К( | К* | К) | К{

Эта грамматика, так же как и рассмотренная выше, описывает два типа коммен­тариев, допустимых в языке программирования Borland Pascal.

Конечные автоматы

Определение конечного автомата

Конечным автоматом (КА) называют пятерку следующего вида: M(Q,V,8,qo,F),

где

• Q, — конечное множество состояний автомата;

• V — конечное множество допустимых входных символов (алфавит автомата);

• 5 — функция переходов, отображающая VxQ (декартово произведение мно­жеств) в множество подмножеств Q: R(Q), то есть 8(a,q) = R, ае V, qeQ, RcOj

• q₀ — начальное состояние автомата Q, q₀eOj

• F — непустое множество конечных состояний автомата, FcQ, F*0.

КА называют полностью определенным, если в каждом его состоянии сущест­вует функция перехода для всех возможных входных символов, то есть VaeV, VqeQ38(a,q) = R, RcQ.

Работа конечного автомата представляет собой последовательность шагов (или тактов). На каждом шаге работы автомат находится в одном из своих состояний Q (в текущем состоянии), на следующем шаге он может перейти в другое состоя­ние или остаться в текущем состоянии. То, в какое состояние автомат перейдет на следующем шаге работы, определяет функция переходов 8. Она зависит не только от текущего состояния, но и от символа из алфавита V, поданного на вход автомата. Когда функция перехода допускает несколько следующих состояний автомата, то КА может перейти в любое из этих состояний. В начале работы ав­томат всегда находится в начальном состоянии q₀. Работа КА продолжается до тех пор, пока на его вход поступают символы из входной цепочки coeV⁺.

Видно, что конфигурацию КА на каждом шаге работы можно определить в виде (q,co,n), где q — текущее состояние автомата, qeQj со — цепочка входных симво­лов, соеV⁺; n — положение указателя в цепочке символов, neNu{0}, п < |co| (N — множество натуральных чисел). Конфигурация автомата на следующем шаге — это (q',co,n+l), если q'e8(a,q) и символ aeV находится в позиции п+1 цепочки со. Начальная конфигурация автомата: (q₀,co,0); заключительная конфигурация ав­томата: (f,co,n), feQ,, n = |со|, она является конечной конфигурацией, если feF.

КА M(Q,V,S,qo,F) принимает цепочку символов coeV⁴, если, получив на вход эту цепочку, он из начального состояния q₀ может перейти в одно из конечных со­стояний feF. В противном случае КА не принимает цепочку символов.

Язык ЦМ), заданный КА М(О,У,8^₀,Р), — это множество всех цепочек симво­лов, которые принимаются этим автоматом. Два КА эквивалентны, если они за­дают один и тот же язык.

Таким образом, КА является распознавателем для формальных языков. Далее будет показано, что КА — это распознаватели для регулярных языков.

КА часто представляют в виде диаграммы или графа переходов автомата.

Граф переходов КА — это направленный помеченный граф, с символами состоя­ний КА в вершинах, в котором есть дуга (p,q) p,qeQ, помеченная символом aeV, если в КА определена 5(а,р) и qe8(a,p). Начальное и конечные состояния авто­мата на графе состояний помечаются специальным образом (в данном пособии начальное состояние — дополнительной пунктирной линией, конечное состоя­ние — дополнительной сплошной линией).

Рассмотрим конечный автомат: M({H,A,B,S}.{a,b},8,H,{S}); 8: 8(H,b) = В, 8(В,а) = А, 8(A,b) = {B,S}. Ниже на рис. 10.1 приведен пример графа состояний для этого КА.

" b а ^ь^=^

р

Рис. 10.1. Граф переходов недетерминированного конечного автомата

Для моделирования работы КА его удобно привести к полностью определенно­му виду, чтобы исключить ситуации, из которых нет переходов по входным сим­волам. Для этого в КА добавляют еще одно состояние, которое можно условно назвать «ошибка». На это состояние замыкают все неопределенные переходы, а все переходы из самого состояния «ошибка» замыкают на него же.

Если преобразовать подобным образом рассмотренный выше автомат М, то по­лучим полностью определенный автомат: M({H,A,B,E,S},{a,b},8,H,{S}); 8: 8(Н,а) = Е, 8(H,b) = B, 8(B,a) = A, 8(B,b) = E, 8(A,a) = {E}, 8(A,b) = {B,S}, 8(E,a) = {Е}, 8(E,b) = {E}, 8(S,a) = {E}, 8(S,b) = {Е}. Состояние Е как раз соответствует состоянию «ошиб­ка». Граф переходов этого КА представлен на рис. 10.2.

,_.. Ь а Ь

а

а,Ь

_*а-

Рис. 10.2. Граф переходов полностью определенного недетерминированного конечного автомата

Детерминированные и недетерминированные конечные автоматы

Конечный автомат M(Q,V,8,q₀,F) называют детерминированным конечным авто­матом (ДКА), если в каждом из его состояний для любого входного символа функ­ция перехода содержит не более одного состояния: VaeV, VqeQ; либо S(a,q) = {г}, reQ либо 8(a,q) = 0.

В противном случае конечный автомат называют недетерминированным. ДКА может быть задан в виде пятерки:

M(Q,V,5,q₀,F),

где Q — конечное множество состояний автомата; V — конечное множество до­пустимых входных символов; 8 — функция переходов, отображающая VxQ e множество Q: S(a,q) = г, aeV, q,reQ; q₀ — начальное состояние автомата Q q₀eQ; F — непустое множество конечных состояний автомата, FcQ F*0.

Если функция переходов ДКА определена для каждого состояния автомата, тс автомат называется полностью определенным ДКА: VaeV, VqeQ: либо 38(a,q) = r reQ.

Моделировать работу ДКА существенно проще, чем работу произвольного ДКА.

Доказано, что для любого ДКА можно построить эквивалентный ему ДКА. По­этому используемый произвольный ДКА А стремятся преобразовать в ДКА. При построении компиляторов чаще всего используют полностью определеный ДКА.

Преобразование конечного автомата к детерминированному виду

Алгоритм преобразования произвольного ДКА M(Q₎V,8,q₀,F) в эквивалентный ему ДКА M'(Q',V,S',q'₀,F') заключается в следующем:

1. Множество состояний Q' автомата М' строится из комбинаций всех состоя­ ний множества Q автомата М. Если qi,q₂ q_n, n > 0 — состояния автомата М

V0<i<n qjeQ, то всего будет 2^п-1 состояний автомата М'. Обозначим ю так: [q,,q₂,...,q_m], 0<m<n.

2. Функция переходов 8' автомата М' строится так: 8'(a,[q₁,q₂,...,q_m]) = [г^г^л-Л] где V0 < i < m Э0 < j < k так, что 8(а^) = г,;

3. Обозначим q'₀ = [q₀];

4. Пусть f^.-jfi, 1 > 0 — конечные состояния автомата М, V0 < i < 1 f^eF, тогдг множество конечных состояний F' автомата М' строится из всех состояний имеющих вид [...,1,,...], fjeF.

Доказано, что описанный выше алгоритм строит ДКА, эквивалентный заданно­му произвольному КА.

После построения из нового ДКА необходимо удалить все недостижимые со­стояния.

Состояние qeQ в КА M(QV,S,q₀,F) называется недостижимым, если ни при ка­кой входной цепочке юе V⁺ невозможен переход автомата из начального состоя­ния q₀ в состояние q. Иначе состояние называется достижимым.

Для работы алгоритма удаления недостижимых состояний используются двг множества: множество достижимых состояний R и множество текущих актив­ных состояний на каждом шаге алгоритма Р_г Результатом работы алгоритма яв­ляется полное множество достижимых состояний R. Рассмотрим работу алгоритма по шагам:

1. R:={q₀}; i:=0; P₀:={q₀};

2. P_i+1:=0;

3. VaeV, VqePj: P_i+1:-P_i+1u8(a,q);

4. Если Pi+i-R = 0, то выполнение алгоритма закончено, иначе R:=RuP_i+1, i:=i+l и перейти к шагу 3.

После выполнения данного алгоритма из КА можно исключить все состояния, не входящие в построенное множество R.

Рассмотрим работу алгоритма преобразования произвольного КА в ДКА на при­мере автомата M({H,A,B,S},{a.b},8,H,{S}); 5: 8(H,b) «- В, 8(В,а) = А, 5(А,Ь) = {B.S}. Видно, что это недетерминированный КА (из состояния А возможны два раз­личных перехода по символу Ь). Граф переходов для этого автомата был изобра­жен выше на рис. 10.1.

Построим множество состояний эквивалентного ДКА:

Q'={[H].[A],[B].[S].[HA],[HB].[HS].[AB],[AS],[BS].[HAB].[HAS].[HBS]. [ABS].[HABS]}.

Построим функцию переходов эквивалентного ДКА:

8'([Н],Ь)	= [B]
8'([А],Ь)	H [BS]
8'([В],а)	- [A]
8Х[НА],Ь)	= [BS]
8'([НВ],а)	= [A]
8'([НВ],Ь)	= [B]
5'([HS],b)	= [B]
8'([АВ],а)	= [A]
8Х[АВ],Ь)	= [BS]
8'([AS],b)	= [BS]
S'([BS],a)	- [A]
8'([НАВ],а)	= [A]
8X[HAB],b)	- [BS]
8X[HAS],b)	= [BS]
8X[HBS],b)	- [B]
8X[HBS],a)	= [A]
8X[ABS],b)	= [BS]
8X[ABS],a)	= [A]
SX[HABS],a)	= [A]
SX[HABS],b)	- [BS]

Начальное состояние эквивалентного ДКА:

Qo' = [Н] Множество конечных состояний эквивалентного ДКА:

F' - {[S].[HS].[AS].[BS].[HAS].[HBS].[ABS].[HABS]}

После построения ДКА исключим недостижимые состояния. Множество дости­жимых состояний ДКА будет следующим R = {[H],[B],[A],[BS]}. В итоге, ис­ключив все недостижимые состояния, получим ДКА:

M4{[H].[B].[A].[BS]}.{a.b}.[H].{[BS]}).

S([H].b)=[B]. 5([B].a)-[A]. 8([A],b)=[BS]. 5([BS].a)=[A].

Ничего не изменяя, переобозначим состояния ДКА. Получим:

M'({H.B.A.S}.{a.b}.H.{S}).

5(H.b)=B. 6(B.a)=A. 8(A.b)=S. 5(S,a)-A.

Граф переходов полученного ДКА изображен на рис. 10.3.

Рис. 10.3. Граф переходов детерминированного конечного автомата

Этот автомат можно преобразовать к полностью определенному виду. Получим граф состояний, изображенный на рис. 10.4 (состояние Е — это состояние «ошиб­ка»).

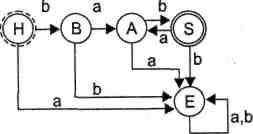
Рис. 10.4. Граф переходов полностью определенного детерминированного конечного автомата

При построении распознавателей к вопросу о необходимости преобразования К/ в ДКА надо подходить, основываясь на принципе разумной достаточности. Мо делировать работу ДКА существенно проще, чем произвольного КА, но при вы полнении преобразования число состояний автомата может существенно возрас ти и, в худшем случае, составит 2^п-1, где п — количество состояний исходноп КА. В этом случае затраты на моделирование ДКА окажутся больше, чем на моделирование исходного КА. Поэтому не всегда выполнение преобразования ав томата к детерминированному виду является обязательным.

Минимизация конечных автоматов

Многие КА можно минимизировать. Минимизация КА заключается в построе нии эквивалентного КА с меньшим числом состояний. В процессе минимизаци необходимо построить автомат с минимально возможным числом состояний, эквивалентный данному КА.

Для минимизации автомата используется алгоритм построения эквивалентны состояний КА. Два различных состояния в конечном автомате M(Q,V,5,q₀,F

qeQ,и q'eQ. называются п-эквивалентными (n-неразличимыми), п > О neNu{0}, если, находясь в одном из этих состояний и получив на вход любую цепочку символов со: <oeV* |co| < п, автомат может перейти в одно и то же множество конеч­ных состояний. Очевидно, что эквивалентными состояниями автомата M(Q,V, 5,q₀,F) являются два множества его состояний: F и Q-F. Множества эквивалент­ных состояний автомата называют классами эквивалентности, а всю их совокуп­ность — множеством классов эквивалентности R(n) причем R(0)={F,Q,-F}.

Рассмотрим работу алгоритма построения эквивалентных состояний по шагам:

1. На первом шаге п:=0 строим R(0).

1. На втором шаге п:=п+1 строим R(n) на основе R(n-l): R(n) = {Г((п): {qjjeQj VaeV 8(a,qjj)cij(n-l)} VijeN}. To есть в классы эквивалентности на шаге п входят те состояния, которые по одинаковым символам переходят в п-1 эк­вивалентные состояния.

2. Если R(n) = R(n-l), то работа алгоритма закончена, иначе необходимо вер­нуться к шагу 2.

Доказано, что алгоритм построения множества классов эквивалентности завер­шится максимум для n = m-2, где т — общее количество состояний автомата.

Алгоритм минимизации КА заключается в следующем:

1. Из автомата исключаются все недостижимые состояния.

2. Строятся классы эквивалентности автомата.

3. Классы эквивалентности состояний исходного КА становятся состояниями ре­зультирующего минимизированного КА.

4. Функция переходов результирующего КА очевидным образом строится на ос­нове функции переходов исходного КА.

Для этого алгоритма доказано, во-первых, что он строит минимизированный КА, эквивалентный заданному; во-вторых, что он строит КА с минимально возмож­ным числом состояний (минимальный КА).

Рассмотрим пример: задан автомат M({A,B,C,D,E,F,G},{0,1},5,A,{D,E}), 5(A,0) = {В}, 5(А,1) = {С}, 8(В,1) = {D}, 5(С,1) = {Е}. 5CD.0) = {С}, 5(0,1) = {Е}, 5(Е,0) = {В}, 5(E.l) = {D}, 5(F,0) = {D}, 5(F.l) = {G}, 5(G,0) = {F}, 5(G,1) = {F}; необходимо построить эквивалентный ему минимальный КА.

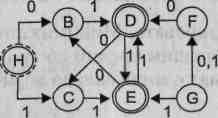
Рис. 10.5. Граф переходов конечного автомата до его минимизации

Состояния F и G являются недостижимыми, они будут исключены на первом шаге алгоритма. Построим классы эквивалентности автомата:

R(0)={{A,B,C},{D,E}}, n=0;

R(1)={{A},{B.C},{D,E}}, n=l;

R(2)={{A},{B,C},{D,E}}, n=2.

Обозначим соответствующим образом состояния полученного минимального КА и построим автомат: M({A.BC,DE},{0,1},5',A,{DE}), 5'(А,0) = {ВС}, 5'(А,1) = {ВС} 5ЧВС.1) = {DE}, 54DE.0) = {ВС}, 54DE.1) = {DE}.

Граф переходов минимального КА приведен на рис. 10.6.

Рис. 10.6. Граф переходов конечного автомата после его минимизации

Минимизация конечных автоматов позволяет при построении распознавателей получить автомат с минимально возможным числом состояний и тем самым г дальнейшим упростить функционирование распознавателя.

Регулярные множества и регулярные выражения

Определение регулярного множества

Определим над множествами цепочек символов из алфавита V операции конка­тенации и итерации следующим образом:

PQ - конкатенация PeV* и QeV*: PQ = {pq VpeP, VqeQJ; P* - итерация PeV*: P* = {pⁿ VpeP, VneN}.

Тогда для алфавита V регулярные множества определяются рекурсивно:

1. 0 — регулярное множество.

2. {к} — регулярное множество.

3. {а} — регулярное множество VaeV.

4. Если Р и Q. — произвольные регулярные множества, то множества PuQ, PC и Р* также являются регулярными множествами.

5. Ничто другое не является регулярным множеством.

Фактически регулярные множества — это множества цепочек символов над за­данным алфавитом, построенные определенным образом (с использованием опе­раций объединения, конкатенации и итерации).

Все регулярные языки представляют собой регулярные множества.

Регулярные выражения. Свойства регулярных выражений

Регулярные множества можно обозначать с помощью регулярных выражений. Эти обозначения вводятся следующим образом:

1. 0 — регулярное выражение, обозначающее 0.

2. X — регулярное выражение, обозначающее {X}.

3. а — регулярное выражение, обозначающее {a} VaeV.

4. Если р и q — регулярные выражения, обозначающие регулярные множества Р и Q, то p+q, pq, p* — регулярные выражения, обозначающие регулярные мно­жества PuQ, PQ и Р* соответственно.

Два регулярных выражения а и (3 равны, а = Р, если они обозначают одно и то же множество.

Каждое регулярное выражение обозначает одно и только одно регулярное мно­жество, но для одного регулярного множества может существовать сколь угодно много регулярных выражений, обозначающих это множество.

При записи регулярных выражений будут использоваться круглые скобки, как и для обычных арифметических выражений. При отсутствии скобок операции вы­полняются слева на право с учетом приоритета. Приоритет для операций принят следующий: первой выполняется итерация (высший приоритет), затем конкате­нация, потом — объединение множеств (низший приоритет).

Если а, р и у — регулярные выражения, то свойства регулярных выражений можно записать в виде следующих формул:

1.	^+а<х* г А.+а*а = а*
2.	а+Р = р+аЗ.
3.	а+(Р+у) = (а+р)+у
4.	а(Р+У) ? оф+ау
5.	(Р+у)а = Ра+уа
6.	а(Ру) = (ар)у
7.	а+а = а
8.	а+а* *■ а*
9.	Х+а' = а*+Х - а*
10.	0' = Х
П.	0а=а0~0
12.	0+а = а+0"а
13.	tax = аХ = а
14.	(а*)* - а*

Все эти свойства можно легко доказать, основываясь на теории множеств, так как регулярные выражения — это только обозначения для соответствующих множеств. Следует также обратить внимание на то, что среди прочих свойств отсутствует равенство оф = ра, то есть операция конкатенации не обладает свойством комму­тативности. Это и не удивительно, поскольку для этой операции важен порядок следования символов.

Уравнения с регулярными коэффициентами

На основе регулярных выражений можно построить уравнения с регулярными коэффициентами [32]. Простейшие уравнения с регулярными коэффициентами будут выглядеть следующим образом:

X = аХ + р,

Х= Ха + р,

где a,PeV* — регулярные выражения над алфавитом V, а переменная XgV.

Решениями таких уравнений будут регулярные множества. Это значит, что если взять регулярное множество, являющееся решением уравнения, обозначить его в виде соответствующего регулярного выражения и подставить в уравнение, то по­лучим тождественное равенство. Два вида записи уравнений (правосторонняя и левосторонняя запись) связаны с тем, что для регулярных выражений опера­ция конкатенации не обладает свойством коммутативности, поэтому коэффици­ент можно записать как справа, так и слева от переменной и при этом получатся различные уравнения. Обе записи равноправны.

Решением первого уравнения является множество, обозначенное регулярным вы­ражением а*р. Проверим это решение, подставив его в уравнение вместо пере­менной X:

aX+p = a(a*p)+P =⁶ (aa*)P+P =¹³ (aa*)p+ty3 =⁵ (aa*+?,)p -i a*p = X

Над знаками равенства указаны номера свойств регулярных выражений, кото­рые были использованы для выполнения преобразований.

Решением второго уравнения является множество, обозначенное регулярным выражением pa*.

Xa+p = (pa*)a+p =⁶ p(a*a)+p =¹³ P(a*a)+pb =⁴ |3(a'a+X.) ** Pa* = X

Указанные решения уравнений не всегда являются единственными. Например, если регулярное выражение а в первом уравнении обозначает множество, кото­рое содержит пустую цепочку, то решением уравнения может быть любое мно­жество, обозначенное выражением X = а*(Р+у), где у — выражение, обозначаю­щее произвольное множество над алфавитом V (причем это множество даже может не быть регулярным). Однако доказано, что X = а'Р и X = Ра* — это наи­меньшие из возможных решений для данных двух уравнений. Эти решения на­зываются наименьшей подвижной точкой.

Из уравнений с регулярными коэффициентами можно формировать систему уравнений с регулярными коэффициентами. Система уравнений с регулярными коэффициентами имеет вид (правосторонняя запись):

X_t = а₁₀ + a._nXi + а₁₂Х₂ + ... + а_1пХ_п Х₂ = а₂₀ + a₂₁X_t + а₂₂Х₂ + ... + а_2пХ_п

Xj = a_i0 + a_uXi + a_i2X₂ + ... + a_inX_n

X_n = a_n0 + a_nlXj + a₁₂X₂ + ... + a_nnX_n или (левосторонняя запись):

X, = a₁₀ + Xjan + X₂a₁₂ + ... + X_na_ln X₂ = a₂₀ + Х_ха₂1 + X₂a₂₂ + ... + X_na_2n

Xj = a_i0 + XjOit + X₂a_i2 + ... + X_na_in

X_n = a_n0 + X_ta_nl + X₂a₁₂ + ... + X_na_nn

В системе уравнений с регулярными коэффициентами все коэффициенты а^ яв­ляются регулярными выражениями над алфавитом V, а переменные не входят в алфавит V: Vi Xjg V. Оба варианта записи равноправны, но в общем случае могут иметь различные решения при одинаковых коэффициентах при переменных. Чтобы решить систему уравнений с регулярными коэффициентами, надо найти такие регулярные множества Xj, при подстановке которых в систему все уравне­ния превращаются в тождества множеств. Иными словами, решением системы является некоторое отображение f(X) множества переменных уравнения Л={Х|: n > i > 0} на множество языков над алфавитом V*.

Системы уравнений с регулярными коэффициентами решаются методом после­довательных подстановок. Рассмотрим метод решения для правосторонней запи­си. Алгоритм решения работает с переменной номера шага i и состоит из следую­щих шагов.

Шаг 1. Положить i := 1.

Шаг 2. Если i = п, то перейти к шагу 4, иначе записать i-e уравнение в виде: Xj = ajXi+Pi, где a; = a_ii7 Pi = р_ю + Р_И-цХ₁₊₁ + ... + p_inX_n. Решить уравнение и полу­чить Xj = ocj'pj. Затем для всех уравнений с переменными X_i+1,...,X_n подставить в них найденное решение вместо Xj.

Шаг 3. Увеличить i на 1 (i := i+1) и вернуться к шагу 2.

Шаг 4. После всех подстановок уравнение для Х_п будет иметь вид X_n = a_nX_n+p, где a_n = a_nn. Причем р будет регулярным выражением над алфавитом V* (не со­держит в своем составе переменных системы уравнений Xj). Тогда можно найти окончательное решение для X_n: X_n r a_n*p. Перейти к шагу 5. Шаг 5. Уменьшить i на 1 (i := i-1). Если i = 0, то алгоритм завершен, иначе перей­ти к шагу 6.

Шаг 6. Берем найденное решение для Xj = cxjXj+Pj, где оц = a_ii; р₍ = p_i0 + Pii+iX_i+i + + ... + p_inX_n> и подставляем в него окончательные решения для переменных Xj+i Х_п. Получаем окончательное решение для Х_;. Перейти к шагу 5.

Для левосторонней записи системы уравнений алгоритм решения будет анало­гичным, с разницей только в порядке записи коэффициентов (справа от пере­менных).

Система уравнений с регулярными коэффициентами всегда имеет решение, но это решение не всегда единственное. Для рассмотренного алгоритма решения системы уравнений с регулярными коэффициентами доказано, что он всегда на­ходит решение f(X) (отображение f: Vi Xj->V"), которое является наименьшей неподвижной точкой системы уравнений. То есть если существует любое другое решение g(X), то всегда f(X)cg(X).

В качестве примера рассмотрим систему уравнений с регулярными коэффици­ентами над алфавитом V = {"-", "+", ".", О, 1, 2, 3, 4, 5, 6, 7, 8, 9} (для ясности за­писи символы -, + и . взяты в кавычки, чтобы не путать их со знаками опера­ций):

Xj = ("-" + "+" + X)

Х₂ = Х₁"."(0+1+2+3+4+5+6+7+8+9) + Х₃"." + Х₂(0+1+2+3+4+5+6+7+8+9)

Х₃ - Х₁(0+1+2+3+4+5+6+7+8+9) + Х₃(0+1+2+3+4+5+6+7+8+9)

х₄ = х₂ + х₃

Обозначим регулярное выражение (0+1+2+3+4+5+6+7+8+9) через а для крат­кости записи: a = (0+1+2+3+4+5+6+7+8+9). Получим:

_Xl = ("-" + "+;; + х)

Х₂ - X,"."a + Х₃"." + Х₂а

Х₃ = XjCt + Х₃а

х₄ = х₂ + х₃

Решим эту систему уравнений. Шаг 1. i := 1.

Шаг 2. Имеем i = 1 < 4. Берем уравнение для i = 1. Имеем Х₁ = ("-" + "+" + X). Это уже и есть решение для Xj. Подставляем его в другие уравнения. Получаем:

Х₂ = ("-" + "+" + ху."а + Х₃"." + Х₂а Х₃ = ("-" + "+" + А.)а + Х₃а

х₄ ⁼ х₂ + х₃

Шаг 3. i:- i + 1 - 2.

Возвращаемся к шагу 2.

Шаг 2. Имеем i = 2 < 4. Берем уравнение для i = 2. Имеем

Х₂ = ("-" + "+" + Х)"."а + Х₃"." + Х₂а. Преобразуем уравнение к виду:

Х₂ = Х₂а + (("-" + "+" + Х)"."а + Х₃"."). Тогда а₂ = а, р₂ = ("-" + "+" + Х)""а + Х₃".". Решением для Х₂ будет:

Х₂ = р₂а₂* - (("-" + "+" + Х)"."а + Х₃".")а* = ("-" + "+" + Х)"."аа' + Х₃"."а*.

Подставим его в другие уравнения. Получаем:

Х₃ = ("-" + "+" + ^)а + Х₃а

Х₄ - ("-" + "+" + ^)"."аа* + Х₃"."а* + Х₃

Шаг 3. i:- i + 1 = 3.

Возвращаемся к шагу 2.

Шаг 2. Имеем i = 3 < 4. Берем уравнение для i = 3. Имеем

Х₃ - ("-" + "+" + Х)а + Х₃а. Преобразуем уравнение к виду

Х₃ = Х₃а + ("-" + "+" + Х)а. Тогда а₃ = а, р₃ = ("-" + "+" + Х)а. Решением для Х₃ будет: Х₃ = (3₃а₃* = ("-" + "+" + ^)аа*. Подставим его в другие уравнения. Получаем:

Х₄ - ("-" + "+" + b)"."aa* + ("-" + "+" + A,)aa*"."a* + ("-" + "+" + X,)aa*.

Шаг 3. i:- i + 1 = 4.

Возвращаемся к шагу 2.

Шаг 2. Имеем i = 4 = 4. Переходим к шагу 4.

Шаг 4. Уравнение для Х₄ теперь имеет вид

Х₄ = ("-" + "+" + ^)"."aa* + ("-" + "+" + ^)aa*"."a* + ("-" + "+" + я,)аа*. Оно не нуждается в преобразованиях и содержит окончательное решение для Х₄. Переходим к шагу 5. Шаг 5. i := i - 1 - 3 > 0. Переходим к шагу 6.

Шаг 6. Уравнение для Х₃ имеет вид Х₃ = ("-" + "+" + X,)aa*. Оно уже содержит окончательное решение для Х₃. Переходим к шагу 5.

Шаг 5. i:- i - 1 = 2 > 0. Переходим к шагу 6.

Шаг 6. Уравнение для Х₂ имеет вид Х₂ = ("-" + "+" + X,)"."aa* + X₃"."a*. Подста­вим в него окончательное решение для Х₃. Получим окончательное решение для Х₂: Х₂ = ("-" + "+" + X.)"."aa* + ("-" + "+" + Я.)аа*"."а*. Переходим к шагу 5.

Шаг 5. i:- i - 1 = 1 > 0. Переходим к шагу 6.

Шаг 6. Уравнение для X_t имеет вид X_t = ("-" + "+" + X). Оно уже содержит окон­чательное решение для Х\. Переходим к шагу 5. Шаг 5. i :=. i - 1 - 0'- 0. Алгоритм завершен. В итоге получили решение:

Xj = ("-" + "+" + X)

Х₂ - ("-" + "+" + Х)"."аа + ("-" + "+" + >.)aa*"."a* Х₃ = ("-" + "+" + ^)аа

Х₄ = ("-" + "+" + %)".Ш' + ("-" + "+" + ^)aa*".V + ("-" + "+" + A.)aa*

Выполнив несложные преобразования, это же решение можно представить в бо­лее простом виде:

Х₁ = ("-" + "+" + X)

Х₂ = ("_" + "+" + Х)("."а + aa*".")a*

Х₃ - ("-" + "+" + ^)aa*

Х₄ = ("-" + "+" + Х)("."а + aa*"." + a)a*

Если подставить вместо обозначения а соответствующее ему регулярное выра­жение a = (0+1+2+3+4+5+6+7+8+9), то можно заметит, что регулярное выраже­ние для Х₄ описывает язык десятичных чисел с плавающей точкой.

Способы задания регулярных языков

Три способа задания регулярных языков

Регулярные (праволинейные и леволинейные) грамматики, конечные автоматы (КА) и регулярные множества (равно как и обозначающие их регулярные выра­жения) — это три различных способа, с помощью которых можно задавать регу­лярные языки. Регулярные языки в принципе можно определять и другими способами, но именно три указанных способа представляют наибольший инте­рес.

Доказано, что все три способа в равной степени могут быть использованы для определения регулярных языков. Для них можно записать следующие утвержде­ния:

Утверждение 2.1. Язык является регулярным множеством тогда и только тогда, когда он задан леволинейной (праволинейной) грамматикой.

Утверждение 2.2. Язык может быть задан леволинейной (праволинейной) грам­матикой тогда и только тогда, когда он является регулярным множеством.

Утверждение 2.3. Язык является регулярным множеством тогда и только тогда, когда он задан с помощью конечного автомата.

Утверждение 2.4. Язык распознается с помощью конечного автомата тогда и только тогда, когда он является регулярным множеством.

Все три способа определения регулярных языков эквивалентны. Существуют ал­горитмы, которые позволяют для регулярного языка, заданного одним из ука­занных способов, построить другой способ, определяющий тот же самый язык. Это не всегда справедливо для других способов, которыми можно определить регулярные языки. Ниже рассмотрены некоторые из таких алгоритмов.

Связь регулярных выражений и регулярных грамматик

Регулярные выражения и регулярные грамматики связаны между собой следую­щим образом:

• для любого регулярного языка, заданного регулярным выражением, можно по­строить регулярную грамматику, определяющую тот же язык;

• для любого регулярного языка, заданного регулярной грамматикой, можно по­лучить регулярное выражение, определяющее тот же язык.

Ниже будут рассмотрены два алгоритма, реализующие эти преобразования. В ал­горитмах будут использоваться леволинейные грамматики и леволинейная за­пись уравнений с регулярными коэффициентами, но очевидно, что все то же самое справедливо также для праволинейных грамматик и праволинейной запи­си уравнений.

Построение леволинейной грамматики для языка, заданного регулярным выражением

Регулярные множества (и обозначающие их регулярные выражения) заданы с помощью рекурсивного определения. Будем строить леволинеиную грамматику для регулярного выражения над алфавитом V, следуя шагам этого определения.

1. Для регулярного выражения 0 построим леволинеиную грамматику G(V, {S},0,S), которая будет определять язык, заданный этим выражением (грам­матика, в которой нет ни одного правила).

2. Для регулярного выражения X построим леволинеиную грамматику G(V,{S}, {S—>A.},S), которая будет определять язык, заданный этим выражением.

3. Для регулярного выражения aeV построим леволинеиную грамматику G(V, (S},{S-»a},S), которая будет определять язык, заданный этим выражением.

4. Имеем регулярные выражения аир, заданные ими языки Ц и L₂, а также со­ ответствующие им леволинейные грамматики G^V.VNt.Pj.S!) и G₂(V,VN₂, P₂,S₂): Ц = L(G₄) и L₂ = L(G₂). Необходимо на основе этих данных построить леволинейные грамматики для языков, заданных выражениями а+р (L₃ = = Lj и L₂), ар (L₄ = L,L₂) и а* (L₅ = Ц*): О для языка, заданного выражением а+р, строим грамматику G₃(V,VN₃,P₃,S₃):

VN₃ = VNi u VN₂ u {S₃} (алфавит нетерминальных символов G₃ строится на основе алфавитов нетерминальных символов Gj и G₂ с добавлением но-' вого символа S₃), P₃ = P_t u Р₂ и {S₃-»S₂|Si} (множество правил G₃ строит­ся на основе множеств правил G] и G₂ с добавлением двух новых правил S₃—>S₂lS_t), целевым символом грамматики G₃ становится символ S₃; О для языка, заданного выражением ар, строим грамматику G₄(V,VN₄,P₄,S₂): VN₃ r VNj u VN₂ (алфавит нетерминальных символов G₃ строится на ос­нове алфавитов нетерминальных символов G_t и G₂), множество правил Р₄ строится на основе множеств правил P_t и Р₂ следующим образом: все правила из множества Р₄ переносятся в Р₄,

если правило из множества Р₂ имеет вид А-»Ву, A,BeVN₂, yeV, то оно г реносится в Р₄ без изменений,

если правило из множества Р₂ имеет вид А->у, Ае VN₂, ye V", то в Р₄ доба ляется правило A-^S₁y,

целевым символом грамматики G₄ становится целевой символ граммат ки G₂ - S₂;

- для языка, заданного выражением а*, строим грамматику G₅(V,VN₅,P₅,S VN₃ = VNj U {S₅} (алфавит нетерминальных символов G₃ строится на с нове алфавита нетерминальных символов Gj с добавлением нового симв ла S₅), множество правил Р₅ строится на основе множеств правил ', следующим образом:

если правило из множества Pt имеет вид А-»Ву, А,ВеVN_1; yeV*, то оно б реносится в Р₅ без изменений,

если правило из множества Pi имеет вид А-»у, АеVN₂, yeV*, то в Р₅ доба ляются два правила A—>S₁y|y,

дополнительно в Р₅ добавляются два новых правила S₅—>S₁|A., целевым си волом грамматики G₃ становится символ S₅.

Используя указанные построения в качестве базиса индукции, на основе матем тической индукции можно доказать, что для любого регулярного языка, заданн го регулярным выражением, можно построить определяющую этот язык левол нейную грамматику.

Для любого произвольного регулярного выражения, напрямую применяя ра смотренные выше выкладки, можно построить леволинеиную грамматику, опр деляющую заданный этим выражением язык. Начинать построение надо от эл ментарных операндов выражения: символов, пустых цепочек и пустых множеств Построение необходимо вести в порядке выполнения операций выражения.

Построение регулярного выражения для языка, заданного леволинейной грамматикой

Имеем леволинеиную грамматику G(VT,VN,P,S), необходимо найти регуляр» выражение над алфавитом VT, определяющее язык L(G), заданный этой грамм тикой.

В данном случае преобразование не столь элементарно. Выполняется оно следующим образом:

1. Обозначим символы алфавита нетерминальных символов VN следующим о разом: VN = {X_t, X₂, ..., Х„}. Тогда все правила грамматики будут иметь ви X,—»Х/у или X,—>у X;,X_;eVN, yeVT*; целевому символу грамматики S буд соответствовать некоторое обозначение X*.

2. Построим систему уравнений с регулярными коэффициентами на основе п ременных Х_1;Х₂,...,Х„:

Xi = a₀i + Xjttj, + Х₂а₂₁ + ... + Х„а„!

Х₂ = а₀₂ + Х1ОЧ2 ⁺ Х₂а₂₂ + ... + Х_па_п2

Х_п = а_0п + Хдац, + Х₂а_2п + ... + X_na_nn;

коэффициенты a₀i, a₀₂,..., а_0п выбираются следующим образом: a_0i = (Yi ⁺ Y2 ^{+ +} - ⁺ Ут)> ^{если во} множестве правил Р грамматики G существуют правила Х₄—>Y₁ly₂l...JYm' ^{и a}oi⁼ 0> ^если правил такого вида не существует; коэффициенты а^, сы, ..., a_jn для некоторого j выбираются следующим обра­зом: otji = (y_t + у₂ + ... + Ym)>^{если в0} множестве правил Р грамматики G сущест­вуют правила Xj—>XjYi|XjY₂|...lXjy_m, и о^ = 0, если правил такого вида не суще­ствует.

3. Находим решение построенной системы уравнений.

Доказано, что решение для Х_к (которое обозначает целевой символ S граммати­ки G) будет представлять собой искомое регулярное выражение, обозначающее язык, заданный грамматикой G. Остальные решения системы будут представ­лять собой регулярные выражения, обозначающие понятия грамматики, соответ­ствующие ее нетерминальным символам. В принципе для поиска регулярного выражения, обозначающего весь язык, не нужно искать все решения — достаточ­но найти решение для Х_к, если выражения для понятий грамматики не представ­ляют отдельного интереса.

Например, рассмотрим леволинейную грамматику, определяющую язык деся­тичных чисел с плавающей точкой G({".", "-". "+", "О", "1", "2". "3", "4", "5", "6", "7", "8", "9"}, {<знак>, <дробное>, <целое>, <число>},Р,<число>):

Р:

<знак> -> -' | +\'%

<дробное> -> <знак>.0 | <знак>.1 | <знак>.2 | <знак>.3 | <знак>.4 | <знак>,5 | <знак>.6 | <знак>.7 | <знак>.8 | <знак>.9 | <целое>. | <дробное>0 | <дробное>1 | <дробное>2 | <дробное>3 | <дробное>4 | <дробное>5 | <дробное>6 | <дробное>7 | <дробное>8 | <дробное>9 <целое> -> <знак>0 | <знак>1 | <знак>2 | <знак>3 | <знак>4 | <знак>5 | <знак>6 | <знак>7 | <знак>8 | <знак>9 | <целое>0 | <целое>1 | <целое>2 | <целое>3 | <целое>4 | <целое>5 | <целое>6 | <целое>7 | <целое>8 | <целое>9 <число> -» <дробное> | <целое> Обозначим символы множества VN = {<знак>, <дробное>, <целое>, <число>} соот­ветствующими переменными Хр получим: VN = {Xl Х₂, Х₃, Х₄}. Построим систему уравнений на основе правил грамматики G:

Xj = ("-•• + "+" + X)

Х₂ = Xj"."(0+1+2+3+4+5+6+7+8+9) + Х₃"." + Х2(0+1+2+3+4+5+6+7+8+9)

Х₃ « X _t(0+1+2+3+4+5+6+7+8+9) + Х₃(0+1+2+3+4+5+6+7+8+9)

Х₄ = Х₂ + Х₃ Эта система уравнений уже была решена выше. В данном случае нас интересует только решение для Х₄, которое соответствует целевому символу грамматики G <число>. Решение для Х₄ может быть записано в виде: Х₄ = ("-" + "+" + X) ("."(0+1+2+3+4+5+6+7+8+9) + (0+1+2+3+4+5+6+7+8+9) (O+l+2+3-t +4+5+6+7+8+9)*"." + (0+1+2+3+4+5+6+7+8+9)) (0+1+2+3+4+5+6+7+8+9)*

Это и есть регулярное выражение, определяющее язык, заданный грамматикой G.

Связь регулярных выражений и конечных автоматов

Регулярные выражения и конечные автоматы связаны между собой следующим образом:

• для любого регулярного языка, заданного регулярным выражением, можнс построить конечный автомат, определяющий тот же язык;

• для любого регулярного языка, заданного конечным автоматом, можно полу­чить регулярное выражение, определяющее тот же язык.

Ниже будет рассмотрен алгоритм, реализующий построение конечного автомате по регулярному выражению. Алгоритм построения регулярного выражения пс конечному автомату здесь не рассматривается — он не представляет интереса поскольку, как будет показано ниже, проще построить грамматику, эквивалент­ную заданному конечному автомату, а потом уже найти регулярное выражение для заданного грамматикой языка (по алгоритму, который уже был выше рас­смотрен) [5, 6, т. 1, 12, 26].

Построение конечного автомата для языка, заданного регулярным выражением

Регулярные множества (и обозначающие их регулярные выражения) заданы ( помощью рекурсивного определения. Будем строить КА для регулярного выра­жения над алфавитом V, следуя шагам этого определения.

1. Для регулярного выражения 0 построим КА M(Q,= {H,F},V,5,H,{F}), у кото рого функция переходов VqeQ, VaeV имеет вид 5(q,a) = 0.

2. Для регулярного выражения X построим КА M(Q= {F},V,5,F,{F}), у которой функция переходов VaeV имеет вид 8(F,a) = 0, а множество конечных со­стояний содержит только начальное состояние.

3. Для регулярного выражения asV построим КА M(Q= {H,F},V,8,H,{F}), с функ цией переходов 8(Н,а) = {F}.

4. Имеем регулярные выражения аир, заданные ими языки L_t и L₂, а также со ответствующие им КА M^Qj.V.SLq^F,) и M₂(Q₂,V,5₂,q₂,F₂): L_{ = L(Mi) 1 L₂ = L(M₂). Необходимо на основе этих данных построить КА для языков, за данных выражениями а+р (L₃ = Lj u L₂), ар (L₄ = L₍L₂) и а* (L₅ - L/).

О для языка, заданного выражением а+р, строим КА M₃(Q₃,V,5₃,q₃,F₃): Оз г Qi u Q2 Ч {Яз} (множество состояний М₃ строится из множеств со стояний М( и М₂ с добавлением нового состояния q₃),

§з(Яз>а) = S^qj.a) u 5₂(q₂,a) VaeV, 5₃(q,a) = 5,(q,a) VaeV VqeQ,,

8₃(q,a) = 5₂(q,a) VaeV VqeQa,

F₃ = F_t О F₂ О {q₃}, если a+p содержит X, или F₃ = F_t и F₂, если a+p не со­держит X, начальным состоянием КА М₃ становится состояние q₃;

- для языка, заданного выражением ар, строим КА M₄(Q4,V,8₄,qi,F₄):

Q4 = Qi V Q2 (множество состояний М₄ строится из множеств состояний

Mj и М₂),

5₄(q,a) = ЩЩк) VaeV ЧЩ%/*д\

5₄(q,a) = 8!(q,a) и 8₂(q₂,a) VaeV VqeF_t,

8₄(q,a) = 8₂(q,a) VaeV VqeQ,,

F₄ = F₂, если q₂gF₂ или F₄ = Щ и F₂, если q₂eF₂,

начальным состоянием К А М₃ становится начальное состояние К A M_t — q₍; О для языка, заданного выражением а*, строим КА M₅(Q5,V,85,q5,F₅):

Q5 = Q.! u {qs} (множество состояний М5 строится из множества состояний

M_t с добавлением нового состояния q₅),

5₅(q,a) - 8,(q,a) VaeV Vqe(Q₁/F₁),

8₅(q,a) = 8i(q,a) u S^q^a) VaeV VqeF_t,

8₅(q₅.a) Г 8i(q!,a) VaeV,

F5 = Fi О {q₅}, >m

начальным состоянием КА М₅ становится состояние q₅. Используя указанные построения в качестве базиса индукции, на основе матема­тической индукции можно доказать, что для любого регулярного языка, заданно­го регулярным выражением, можно построить определяющий этот язык КА. Построение КА на основе регулярного выражения выполняется аналогично по­строению леволинейной грамматики.

Связь регулярных грамматик и конечных автоматов

На основе имеющейся регулярной грамматики можно построить эквивалентный ей конечный автомат и, наоборот, для заданного конечного автомата можно по­строить эквивалентную ему регулярную грамматику.

Это очень важное утверждение, поскольку регулярные грамматики используют­ся для определения лексических конструкций языков программирования. Соз­дав автомат на основе известной грамматики, мы получаем распознаватель для лексических конструкций данного языка. Таким образом, удается решить задачу разбора для лексических конструкций языка, заданных произвольной регуляр­ной грамматикой. Обратное утверждение также полезно, поскольку позволяет узнать грамматику, цепочки языка которой допускает заданный автомат. Для построения конечного автомата на основании известной грамматики и для построения грамматики на основании данного конечного автомата используются достаточно простые алгоритмы. Все языки программирования определяют нотацию записи «слева направо». В той же нотации работают и компиляторы. Поэтому далее рассмотрены алгоритмы для леволинейных грамматик.

Построение конечного автомата на основе леволинейной грамматики

Имеется леволинейная грамматика G(VT,VN,P,S), необходимо построить экви­валентный ей конечный автомат M(Q,V,5,q₀,F).

Прежде всего для построения автомата исходную грамматику G необходимо привести к автоматному виду. Известно, что такое преобразование можно вы­полнить для любой регулярной грамматики. Алгоритм преобразования к авто­матному виду был рассмотрен выше, поэтому здесь на данном вопросе останав­ливаться нет смысла. Можно считать, что исходная грамматика G уже является леволинейной автоматной грамматикой.

Тогда построение конечного автомата M(Q,V,8,q₀,F) на основе грамматики G(VT, VN,P,S) выполняется по следующему алгоритму.

Шаг 1. Строим множество состояний автомата 0\ Состояния автомата строятся таким образом, чтобы каждому нетерминальному символу из множества VN грам­матики G соответствовало одно состояние из множества Q автомата М. Кроме того, во множество состояний автомата добавляется еще одно дополнительное состояние, которое будем обозначать Н. Сохраняя обозначения нетерминальных символов грамматики G, для множества состояний автомата М можно записать: Q = VNu{H}.

Шаг 2. Входным алфавитом автомата М является множество терминальных сим­волов грамматики G: V = VT.

Шаг 3. Просматриваем все множество правил исходной грамматики. Если встречается правило вида A->teP, где AeVN, teVT, то в функцию перехо­дов 8(H,t) автомата М добавляем состояние A: AeS(H,t).

Если встречается правило вида A-»BteP, где A.BeVN, teVT, то в функцию пе­реходов 8(B,t) автомата М добавляем состояние A: Ae8(B,t).

Шаг 4. Начальным состоянием автомата М является состояние Н: q₀ = Н.

Шаг 5- Множество конечных состояний автомата М состоит из одного состоя­ния. Этим состоянием является состояние, соответствующее целевому символу грамматики G: F = {S}.

На этом построение автомата заканчивается.

Построение леволинейной грамматики на основе конечного автомата

Имеется конечный автомат M(Q,V,8,q₀,F), необходимо построить эквивалент­ную ему леволинейную грамматику G(VT,VN,P,S). Построение выполняется по следующему алгоритму. Шаг 1. Множество терминальных символов грамматики G строится из алфавита входных символов автомата М: VT = V.

Шаг 2. Множество нетерминальных символов грамматики G строится на основа­нии множества состояний автомата М таким образом, чтобы каждому состоянию автомата, за исключением начального состояния, соответствовал один нетерми­нальный символ грамматики: VN = Q\{qo}.

Шаг 3. Просматриваем функцию переходов автомата М для всех возможных со­стояний из множества Одля всех возможных входных символов из множества V. Если имеем 8(A,t) = 0, то ничего не выполняем.

Если имеем 8(A,t) = {В^Вг^.Д,}, п >0, где AeQ, Vn>i>0: B;eQ, teV, тогда для всех состояний Bj выполняем следующее:

• добавляем правило B_s—>t во множество Р правил грамматики G, если А = q₀;

• добавляем правило B^At во множество Р правил грамматики G, если A*q₀. Шаг 4. Если множество конечных состояний F автомата М содержит только одно состояние F = {F₀}, то целевым символом S грамматики G становится символ мно­жества VN, соответствующий этому состоянию: S = F₀; иначе, если множество конечных состояний F автомата М содержит более одного состояния F = {¥_и F₂,...,F_n}, п>1, тогда во множество нетерминальных символов VN грамматики G добавляется новый нетерминальный символ S: VN = VNu{S}, а во множество пра­вил Р грамматики G добавляются правила: S—»F_i|F₂|...|F_n.

На этом построение грамматики заканчивается.

Пример построения конечного автомата на основе заданной грамматики

Рассмотрим грамматику 6({"а","(","*".")"."{"'"}"}• {S.C.K}, P. S) (символы а, (, *, ), {, } из множества терминальных символов грамматики взяты в кавычки, чтобы выделить их среди фигурных скобок, обозначающих само множество):

Р:

S -> С*) | К}

С -» (* | Са | С{ | С} | С( | С* | С)

К -» { | Ка | К( | К* | К) | К{ Это леволинейная регулярная грамматика. Как было показано выше, ее можно преобразовать к автоматному виду.

Получим леволинейную автоматную грамматику следующего вида: G'({"a","(", "*".")","{"."}"}. {S.SlCCl^.P'.S):

Р':

S -> S,) | К}

S! -» С*

С -> С,* | Са | С{ | С} | С( | С* | С)

С, -» С

К -> { | Ка | К( | К* | К) | К{

Для удобства переобозначим нетерминальные символы Q и S₄ символами D и Е. Получим грамматику G'({"a","С."*",")","{",'■}"}. {S.E.C.D.K}, P\ S):

Р':

S -> Е) | К}

Е -> С*

С -> D* | Са | С{ | С} | С( | С* | С)

О -> (

К -» { | Ка | К( | К* | К) | К{

Построим конечный автомат M(Q,V,8,q₀,F), эквивалентный указанной грамма­тике.

Шаг 1. Строим множество состояний автомата. Получаем: Q=VNu{H} = = {S,E,C,D,K,H}.

Шаг 2. В качестве алфавита входных символов автомата берем множество тер­минальных символов грамматики. Получаем: V = {"а","(","*",")","{ ">"}"}•

Шаг 3. Рассматриваем множество правил грамматики.

Для правил S -> Е) | К} имеем 5(Е,")") = {S}: 5(К,"}") = {S}.

Для правила Е ->• С* имеем 8(С,"*") = {Е}.

Для правил С -» D* | Са | С{ | С} | С( | С* | С) имеем 5(D,"*") = {С}: 5(С."а") = {С}; 5(С,"{") = {С}: 5(С,"}") = {С}; 5(С."(") = {С}: 8(С,"*") = {Е.С}; 8(С,"Г) = {С}.

Для правила D -> ( имеем 5(Н,"(") = {D}.

Для правил К -+ { | Ка | К( | К* | К) | К{ имеем 5(Н,"{") = {К}: 5(К,"а") = {К}: 5(К,"(") = {К}; 8(К,"*") = {К}; 5(К,")") = {К}: 8(К."{") = {К}.

Шаг 4. Начальным состоянием автомата является состояние q₀ = Н.

Шаг 5. Множеством конечных состояний автомата является множество F = {S}.

Выполнение алгоритма закончено.

В итоге получаем автомат M({S.E.CD,К,Н}, {"а","(","*",")","{"."}"}. 8, Н, {S}) с функцией переходов:

8(Н.'	{	') " {<}
5(Н.'	(	') = {0}
5(К,'	а	') = {<}
6(К.'	(	') = {К}
5(К,'	*	') - {к}
5(К.'	)	') = (к}
5СК.'	{	') - {к}
5(К.'	}	') - {S}
5(D.'	*	') ■ (С}
8(С	а	') - {С}
6(С	{	') ■ {С}
8(С.'	}	') - {С}
8(С	(	') - {С}
8(С.'	*	') = {Е.С}

5(С.")") 5(1,"О")

{С} {S}

Граф переходов этого автомата изображен на рис. 10.7.

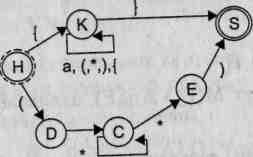
а, (,*,)ДЛ

Рис. 10.7. Недетерминированный КА для языка комментариев в Borland Pascal

Это недетерминированный конечный автомат, поскольку существует состояние, в котором множество, получаемое с помощью функции переходов по одному и тому же символу, имеет более одного следующего состояния. Это состояние С и функция 8(0,"*") - {Е,С}.

Моделировать поведение недетерминированного КА — непростая задача, поэто­му можно построить эквивалентный ему детерминированный КА. Полученный таким путем КА можно затем минимизировать.

В результате всех преобразований получаем детерминированный конечный ав­томат M'({S.E, CD. К, Н},{"а", ■•(»,•'*",")","{". "}"}.5',H.{S}) с функцией переходов:

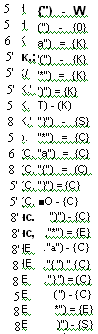
Граф переходов этого автомата изображен на рис. 10.8.

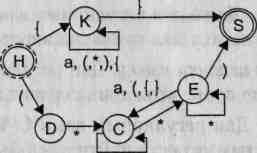
а,(,Ш Рис. 10.8. Детерминированный КАдля языка комментариев в Borland Pascal

На основании этого автомата можно легко построить распознаватель. В данном случае мы можем получить распознаватель для двух типов комментариев языка программирования Borland Pascal, если учесть, что а может означать любой ал­фавитно-цифровой символ, кроме символов (, *, ), {, }.

Свойства регулярных языков

Свойства регулярных языков

Множество называется замкнутым относительно некоторой операции, если в ре­зультате выполнения этой операции над любыми элементами, принадлежащими данному множеству, получается новый элемент, принадлежащий тому же мно­жеству.

Например, множество целых чисел замкнуто относительно операций сложения, умножения и вычитания, но оно не замкнуто относительно операции деления — при делении двух целых чисел не всегда получается целое число.

Регулярные множества (и однозначно связанные с ними регулярные языки) замк­нуты относительно многих операций, которые применимы к цепочкам символов.

Например, регулярные языки замкнуты относительно следующих операций:

• пересечения;

• объединения;

• дополнения;

• итерации;

• конкатенации;

• гомоморфизма (изменения имен символов и подстановки цепочек вместо сим­волов).

Поскольку регулярные множества замкнуты относительно операций пересечения, объединения и дополнения, то они представляют булеву алгебру множеств. Су­ществуют и другие операции, относительно которых замкнуты регулярные мно­жества. Вообще говоря, таких операций достаточно много.

Регулярные языки представляют собой очень удобный тип языков. Для них раз­решимы многие проблемы, неразрешимые для других типов языков. Например, доказано, что разрешимыми являются следующие проблемы.

Проблема эквивалентности. Даны два регулярных языка L_t(V) и L₂(V). Необхо­димо проверить, являются ли эти два языка эквивалентными. Проблема принадлежности цепочки языку. Дан регулярный язык L(V) и цепочка символов cteV*. Необходимо проверить, принадлежит ли цепочка данному языку. Проблема пустоты языка. Дан регулярный язык L(V). Необходимо проверить, является ли этот язык пустым, то есть найти хотя бы одну цепочку а^Х, такую что aeL(V).

Эти проблемы разрешимы вне зависимости от того, каким из трех способов за­дан регулярный язык. Следовательно, эти проблемы разрешимы для всех спосо­бов представления регулярных языков: регулярных множеств, регулярных грам­матик и конечных автоматов. На самом деле достаточно доказать разрешимость любой из этих проблем хотя бы для одного из способов представления языка, то­гда для остальных способов можно воспользоваться алгоритмами преобразова­ния, рассмотренными выше¹.

Для регулярных грамматик также разрешима проблема однозначности — доказа­но, что для любой регулярной грамматики можно построить эквивалентную ей однозначную регулярную грамматику. Это очевидно, поскольку для любой регу­лярной грамматики можно однозначно построить регулярное выражение, опре­деляющее заданный этой грамматикой язык.

Лемма о разрастании для регулярных языков

Иногда бывает необходимо доказать, является или нет некоторый язык регуляр­ным. Конечно, можно пойти путем поиска определения для цепочек заданного языка через один из рассмотренных выше способов (регулярные грамматики, ко­нечные автоматы и регулярные выражения). Если для этого языка хотя бы один из способов будет определен, следовательно, язык является регулярным (и на основании одного найденного способа определения языка можно найти осталь­ные). Но если не удается построить определение языка ни одним из этих спосо­бов, то остается неизвестным: то ли язык не является регулярным, то ли просто не удалось найти определение для него.

Однако существует простой метод проверки, является или нет заданный язык регулярным. Этот метод основан на проверке так называемой леммы о разраста­нии языка. Доказано, что если для некоторого заданного языка выполняется лемма о разрастании регулярного языка, то этот язык является регулярным; если же лемма не выполняется, то и язык регулярным не является [6, т. 1]. Лемма о разрастании для регулярных языков формулируется следующим обра­зом: если дан регулярный язык и достаточно длинная цепочка символов, при­надлежащая этому языку, то в этой цепочке можно найти непустую подцепочку, которую можно повторить сколь угодно много раз, и все полученные таким спо­собом новые цепочки будут принадлежать тому же регулярному языку².

¹ Возможны и другие способы представления регулярных множеств, а для них разреши­мость указанных проблем будет уже не очевидна.

²Если найденную подцепочку повторять несколько раз, то исходная цепочка как бы «раз­ растается» - отсюда и название «лемма о разрастании языков». Формально эту лемму можно записать так: если дан язык L, то 3 константа р > О, такая, что если asL и |а|>р, то цепочку а можно записать в виде а = 8ре, где О < |р| < р, и тогда а' = 8р^!е, a'eL Vi > 0.

Используя лемму о разрастании регулярных языков, докажем, что язык L = {а^пЬ^л | п > 0} не является регулярным.

Предположим, что этот язык регулярный, тогда для него должна выполняться лемма о разрастании. Возьмем некоторую цепочку этого языка a = aⁿbⁿ и запи­шем ее в виде a = 5рБ. Если Реа⁺ или Peb⁺, то тогда для i = 0 цепочка 5р°е = 8е не принадлежит языку L, что противоречит условиям леммы; если же Реа⁺Ь⁺, то­гда для i = 2 цепочка 5p²s = 5рре не принадлежит языку L. Таким образом, язык L не может быть регулярным языком.

Контекстно-свободные языки

Распознаватели КС-языков. Автоматы с магазинной памятью

Определение МП-автомата

Контекстно-свободными (КС) называются языки, определяемые грамматиками типа G(VT,VN,P,S), в которых правила Р имеют вид: А-»р, где AeVN и peV, V=VTuVN.

Распознавателями КС-языков служат автоматы с магазинной памятью (МП-ав­томаты). В общем виде МП-автомат можно определить следующим образом:

RtaV.ZAqo.Zo.F), где Q, — множество состояний автомата; V — алфавит входных символов автома­та; Z — специальный конечный алфавит магазинных символов автомата (обычно он включает в себя алфавиты терминальных и нетерминальных символов грам­матики), VcZ; 8 — функция переходов автомата, которая отображает множество Qx(Vu{?i})xZ на конечное множество подмножеств P(QxZ'); qoeQ. — начальное состояние автомата; z₀eZ — начальный символ магазина; FcQ, — множество ко­нечных состояний.

МП-автомат в отличие от обычного КА имеет стек (магазин), в который можно помещать специальные «магазинные» символы (обычно это терминальные и не­терминальные символы грамматики языка). Переход из одного состояния в дру­гое зависит не только от входного символа, но и от одного или нескольких верхних символов стека. Таким образом, конфигурация автомата определяется тремя

Конфигурация МП-автомата описывается в виде тройки (q,a,eo)eQxV*xZ*, кот< рая определяет текущее состояние автомата q, цепочку еще непрочитанных сил волов а на входе автомата и содержимое магазина (стека) со. Вместо а в конф! гурации можно указать пару (Р,п), где PeV* — вся цепочка входных символо а neNu{0}, п > 0 — положение считывающего указателя в цепочке.

Тогда один такт работы автомата можно описать в виде (q,aa,zco) -s- (q',a,yco), есл (q',y)e8(q,a,z), где q.q'eQ, aeVu{^}, aeV, zeZu{A.}, y,coeZ*. При выполнени такта (перехода) из стека удаляется верхний символ, соответствующий услови перехода, и добавляется цепочка, соответствующая правилу перехода. Первы символ цепочки становится верхушкой стека. Допускаются переходы, при коп рых входной символ игнорируется (и тем самым он будет входным символо при следующем переходе). Эти переходы (такты) называются ^-переходами (^-та тами). Аналогично, автомат не обязательно должен извлекать символ из стека когда z=X,, этого не происходит.

МП-автомат называется недетерминированным, если из одной и той же его ко] фигурации возможен более чем один переход.

Начальная конфигурация МП-автомата, очевидно, определяется как (q₀,a,z₀), ae\ Множество конечных конфигураций автомата — (q,?t,co), qeF, coeZ*.

МП-автомат допускает (принимает) цепочку символов, если, получив эту цепо ку на вход, он может перейти в одну из конечных конфигураций, — когда щ окончании цепочки автомат находится в одном из конечных состояний, а cti содержит некоторую определенную цепочку. Тогда входная цепочка принимаеся (после окончания цепочки автомат может сделать произвольное количесп А.-переходов). Иначе цепочка символов не принимается.

Язык, определяемый МП-автоматом, — это множество всех цепочек символе которые допускает данный автомат. Язык, определяемый МП-автоматом R, об значается как L(R). Два МП-автомата называются эквивалентными, если oi определяют один и тот же язык. Если два МП-автомата Rj и R₂ определяют 0Д1 и тот же язык, это записывается как L(Rj) = L(R2)-

МП-автомат допускает цепочку символов с опустошением магазина, если п] окончании разбора цепочки автомат находится в одном из конечных состояни

а стек пуст — конфигурация (q,X,\), qeF. Если язык задан МП-автоматом R, который допускает цепочки с опустошением стека, это обозначается так: L^(R). Для любого МП-автомата всегда можно построить эквивалентный ему МП-ав­томат, допускающий цепочки заданного языка с опустошением стека. То есть V МП-автомата R: 3 МП-автомат R', такой что L(R) = L^(R').

Кроме обычного МП-автомата существует также понятие расширенного МП-ав­томата.

Расширенный МП-автомат может заменять цепочку символов конечной длины в верхней части стека на другую цепочку символов конечной длины. В отличие от обычного МП-автомата, который на каждом такте работы может изымать из сте­ка только один символ, расширенный МП-автомат может изымать за один такт сразу некоторую цепочку символов, находящуюся на вершине стека. Функция переходов 5 для расширенного МП-автомата отображает множество Qx(Vu{A,})xZ* на конечное множество подмножеств P(QxZ').

Доказано, что для любого расширенного МП-автомата всегда можно построить эквивалентный ему обычный МП-автомат (обратное утверждение очевидно, так как любой обычный МП-автомат является и расширенным МП-автоматом). Та­ким образом, классы МП-автоматов и расширенных МП-автоматов эквивалент­ны и задают один и тот же тип языков.

Эквивалентность языков МП-автоматов и КС-грамматик

Пусть задана КС-грамматика G(VT,VN,P,S). Построим на ее основе МП-автомат R({q},VT,VTuVN,5,q,S,{q}). Этот автомат имеет только одно состояние. Опреде­лим функцию переходов автомата следующим образом:

(q,a)e5(q,X.,A), VA-»a ё Р; (яЛ)е5(я,а,а), Va e VT.

Начальная конфигурация автомата: (q,a,S); конечная конфигурация автомата: (q,U).

Докажем, что данная грамматика и построенный на ее основе автомат определя­ют один и тот же язык. Для этого надо доказать два следующих утверждения:

• если в грамматике G существует вывод А=>*ос, то автомат R может сделать последовательность шагов (q,a,A)-s-*(q,^), где AeVN — некоторый произ­вольный нетерминальный символ грамматики, а aeVT*;

• если автомат R может сделать последовательность шагов (q,a,A)+*(q,X,X), то в грамматике G существует вывод А=>*а.

Докажем первое утверждение. Доказательство будем вести на основе математи­ческой индукции. Положим, что в грамматике G существует вывод A=>^ma для некоторого m > 0.

Для m = 1 имеем А=>а, а = а^-з.^, к>0. Тогда если к = 0, то a = X, и должно су­ществовать правило грамматики А—>Х, а по определению автомата R имеем:

(q,a,A) + (q,A.,A.). Если к > 0, то должно существовать правило грамматики А-»а, и по определению автомата R получаем:

(q,a₁a₂...a_k,A) j (q,a₁a₂...a_k,a₁a₂...a_k) 4- (q,a₂...a_k,a₂...a_k) * ... 4- (q,a_k,a_k) + (q,X,X),

следовательно,

(q,a₁a₂...a_k,A) + (q,a₁a₂...a_k,a₁a₂...a_k) +^k (q,X,X) и (q,a₁a₂...a_k,A) ** (q,X,X).

Таким образом, утверждение для m = 1 доказано.

Предположим, что для некоторого т>1 это утверждение справедливо. Значит, если существует вывод А=>^тгх в грамматике G, то существует и последователь­ность шагов автомата R: (q,a,A) +* (q,X,X).

Следуя принципу математической индукции, докажем теперь, что это утвержде­ние справедливо и для некоторого т+1. То есть докажем, что если существует вывод A=>^m+1a в грамматике G, то существует и последовательность шагов авто­мата R: (q,a,A)+*(q,A,,X,).

Рассмотрим первый шаг вывода A=>^m+1a: A=>X!X₂...X_k, где V k>i>0: Xje(VTuVN). Если X_;eVN, то существует вывод Xj =>^mi x_i; причем XjeVT* и m^m; если же XjeVT, to Xi=Xj. Саму исходную цепочку а можно записать как конкатенацию цепочек терминальных символов х^ a = x_tx₂...x_k.

Если первый шаг вывода А=>Х₁Х₂...Х_к, тогда в грамматике G существует правило А->Х!Х₂...Х_к, и, по определению автомата R, первым шагом его работы может быть шаг: (q,a,A) * (q,a₎X₁X₂..'X_k).

Но для всех XjeVN, так как V k > i > 0: Xj =>^mi ,xj и т_{ < пт, то по утверждению ин­дукции имеем (q^i.Xj) +* (q,X,X).

А для всех X_;eVT по определению автомата R имеем (q.x'^Xj) * (q,X,X).

Объединяя шаги работы автомата R для всех Xj из конфигурации (q,a,X!X₂...X_k), получаем (q,a,X₁X₂...X_k) -гЛ (q,^.,A,), следовательно, (q,a,A) + (q,a,X₁X₂...X_k) +* (q,X,X), и отсюда можно утверждать, что (q,a,A) +* (q,A.,A.).

На основании положений математической индукции утверждение доказано.

Докажем второе утверждение. Доказательство будем вести на основе математи­ческой индукции. Положим, что автомат R может выполнить последовательность шагов (q,a,A) 4^Г (q,X,X) для некоторого п > 0.

Если п = 1, тогда имеем один шаг работы автомата: (q,a,A) -f (q,X,X) и, следова­тельно, a = X. Отсюда, согласно определению автомата R, в грамматике G долж­но существовать правило вида А->А,. Тогда в грамматике G существует и вывод А=>А, или, что то же самое, А=>*а. Для п = 1 утверждение доказано.

Предположим, что для некоторого п>1 это утверждение справедливо. Значит, если существует последовательность шагов работы автомата R: (q,a,A) -ь^п (q,X,X), то в грамматике G существует вывод А=>*а.

Теперь докажем, что это утверждение справедливо и для некоторого п +1. Рас­смотрим последовательность шагов работы автомата R: (q,a,A) -ь^п+1 (q,X,X). Пер­вым шагом этой последовательности будет шаг (q,a,A) + (q,a,X₁X₂...X_k), V k S i > 0: Xje(VTuVN). Причем, по определению автомата R, в грамматике G должно су­ществовать правило вида A-»XiX₂...X_k.

Можно утверждать, что V Xje(VTuVN), (q^.Xj) *ⁿi (q,^), X;eVT*, причем a = Х$£.щ, и в грамматике G существует вывод Х;=>*х_;.

Действительно, если X^VN и (q,Xj,Xi) +ⁿi (q,X,X), X;eVT, то по сделанному пред­положению индукции справедливо утверждение, что существует вывод Х,=>*Х; в грамматике G, так как Vi: nj<n.

Если же Х.еУТ, то по определению автомата R: (q.Xj.Xj) * (q,A-,A,), fcjssXi, что соот­ветствует выводу Х|=>°Х;, и тогда также справедливо Х,=>*Х|. ¹

Тогда можно построить левосторонний вывод в грамматике G: А => Х^.-.Хк =>* Х!Х₂...Х_к =>* Х!Х₂...Х_к =>* ... =>* х^.-.Хк = а. Следовательно, в грамматике G суще­ствует вывод А =>* а.

На основании положений математической индукции утверждение доказано.

Поскольку из двух доказанных утверждений однозначно следует, что в КС-грам­матике G существует вывод S =>* а (где S — целевой символ грамматики) тогда и только тогда, когда в МП-автомате R существует последовательность шагов работы автомата (q,a,S) ■*•* (q,X,X), то можно утверждать, что построенный МП-автомат R распознает язык, заданный КС-грамматикой G: L(R) = L(G). Посколь­ку построенный МП-автомат допускает входные цепочки языка с опустошением стека, то доказано также утверждение L^(R) = L(G).

При доказательстве на структуру правил грамматики G не накладывалось ника­ких дополнительных ограничений, поэтому все доказанные утверждения спра­ведливы для произвольной КС-грамматики.

После того как доказано, что для произвольной КС-грамматики всегда можно построить МП-автомат, распознающий заданный этой грамматикой язык, можно говорить, что МП-автоматы распознают КС-языки. На самом деле существует также и доказательство того, что для произвольного МП-автомата всегда можно построить КС-грамматику, которая задает язык, распознаваемый этим автома­том. Таким образом, КС-грамматики и МП-автоматы задают один и тот же тип языков — КС-языки.

Поскольку класс расширенных МП-автоматов эквивалентен классу обычных МП-автоматов и задает тот же самый тип языков, то можно утверждать, что и расши­ренные МП-автоматы распознают языки из типа КС-языков. Следовательно, язык, который может распознавать расширенный МП-автомат, также может быть за­дан с помощью КС-грамматики.

¹ Здесь используется представление о том, что обозначение «=>*» включает в себя также понятие «вывод с нулевым количеством шагов», которое обозначается «=> » и на самом деле означает, что две цепочки символов совпадают (равны). Если каждая цепочка состо­ит из одного символа, то символы двух цепочек эквивалентны между собой. Эта особен­ность упоминалась, когда вводилось понятие — «а =>* Р» — «цепочка Р выводима из цепочки а», но до настоящего момента явно нигде не использовалась. В данном случае это не влияет на структуру доказательства, но очень удобно, поскольку не требует ввода дополнительного обозначения для понятия «цепочка р выводима из цепочки а или сов­падает с нею».

Детерминированные МП-автоматы

МП-автомат называется детерминированным, если из одной и той же его конф гурации возможно не более одного перехода в следующую конфигурацию.

формально для детерминированного МП-автомата R(Q,V,Z,8,q₀,z₀,F) функщ переходов 8 может VqeQ, VaeV, VzeZ иметь один из следующих трех видов:

1. 5(q,a,z) содержит один элемент: 5(q,a,z) = {(q',y)}, yeZ* и 5(q,^.,z) = 0.

2. 5(q,a,z) = 0 и 5(q,X.,z) содержит один элемент: 8(q,A,,z) = {(q',y)}, yeZ*.

3. 5(q,a,z) = 0 и 5(q,X,z) * 0.

Класс ДМП-автоматов и соответствующих им языков значительно уже, чем ве класс МП-автоматов и КС-языков. В отличие от обычного конечного автома: не для каждого МП-автомата можно построить эквивалентный ему ДМП-авт мат. Иными словами, в общем случае невозможно преобразовать недетермин рованный МП-автомат в детерминированный.

Детерминированные МП-автоматы (ДМП-автоматы) определяют очень важнь класс среди всех КС-языков, называемый детерминированными КС-языкам Доказано, что все языки, принадлежащие к классу детерминированных КС-яз ков, могут быть построены с помощью однозначных КС-грамматик. Посколь однозначность — это важное и обязательное требование в грамматике любого яз ка программирования, ДМП-автоматы представляют особый интерес для созг ния компиляторов. Синтаксический распознаватель цепочек любого языка пр граммирования может быть построен на основе ДМП-автомата.

Кроме того, доказано, что для любого ДМП-автомата всегда можно построй эквивалентный ему ДМП-автомат, который будет учитывать входную цепочку до конца — не допускать бесконечной последовательности ^.-переходов по завершении цепочки [6, т. 1]. Это значительно облегчает моделирование работы ДМ автоматов.

Все без исключения синтаксические конструкции языков программирования : даются с помощью однозначных КС-грамматик (неоднозначность, конечно >: ни в одном компиляторе недопустима). Синтаксические структуры этих язык относятся к классу детерминированных КС-языков и могут распознаваться с г мощью ДМП-автоматов. Поэтому большинство распознавателей, которые бул рассмотрены далее, относятся к классу детерминированных КС-языков.

Свойства КС-языков

Свойства произвольных КС-языков

Класс КС-языков замкнут относительно операции подстановки. Это означа что если в каждую цепочку символов КС-языка вместо некоторого символа ш ставить цепочку символов из другого КС-языка, то получившаяся новая цепоч также будет принадлежать КС-языку. Это основное свойство КС-языков. Формально оно может быть записано так. Если L,L_ai,L_a2,...,L_an — это произвольные КС-языки и {a^.-.a,,} — алфавит язы­ка L, п>0, то тогда язык L' = {х!Х₂...х_к| а^.д-ёЬ, ^xi^eL x₂eL^,..., х_кеЦ_к, к > 0: V к > i > 0: п > j _S > 0} также является КС-языком [6, т. 1].

Например:

L = {0^П1^П | п > 0}, Lo = {a}, L_t = {b^mc^m | m > 0} — это исходные КС-языки, тогда после подстановки получаем новый КС-язык: L' = {aⁿb^mic^mib^m2c^m2...b^mnc^mn | n > 0, Vi:mi>0}.

На основе замкнутости относительно операции подстановки можно доказать дру­гие свойства КС-языков. В частности, класс КС-языков замкнут относительно следующих четырех операций:

• объединения;

• конкатенации;

• итерации;

• гомоморфизма (изменения имен символов).

Интересно, что класс КС-языков не замкнут относительно операции пересече­ния, а поэтому не является классом булевой алгебры. Как следствие, этот класс не замкнут и относительно операции дополнения [6, т. 1].

Например:

L_{ = {aⁿbⁿc^j | п > 0, i > 0} и L₂ = {a^jbⁿcⁿ | n > 0, i > 0} - КС-языки, но L = I^nL, = = {aⁿbⁿcⁿ | n > 0} не является КС-языком (это можно проверить с помощью лем­мы о разрастании КС-языков, которая рассмотрена ниже).

Для КС-языков разрешимы проблема пустоты языка и проблема принадлежно­сти заданной цепочки языку — для их решения достаточно построить МП-авто­мат, распознающий данный язык. Но для КС-языков является неразрешимой проблема эквивалентности двух произвольных КС-грамматик, а, как следствие, также и проблема однозначности заданной КС-грамматики. Не разрешима даже более узкая проблема — проблема эквивалентности заданной произвольной КС-грамматики и произвольной регулярной грамматики.

Тем не менее, хотя в общем случае проблема однозначности для КС-языков не разрешима, для некоторых КС-грамматик можно построить эквивалентную им однозначную грамматику.

Свойства детерминированных КС-языков

Детерминированные КС-языки — это класс тех КС-языков, цепочки которых можно распознавать с помощью ДМП-автоматов. Класс детерминированных КС-языков, естественно, является собственным подмножеством всего класса КС-язы­ков [6, т. 1].

Как уже было сказано ранее, детерминированные КС-языки — это значительно более узкий класс, чем все КС-языки. Класс детерминированных КС-языков не замкнут даже относительно операции объединения, равно как и операции пере­сечения (хотя и замкнут относительно операции дополнения, в отличие от всех КС-языков в целом).

Класс детерминированных КС-языков интересен тем, что для него разрешима проблема однозначности. Доказано, что если язык может быть распознан с помо­щью ДМП-автомата (и потому является детерминированным КС-языком), то он может быть описан на основе однозначной КС-грамматики. Именно поэтому дан­ный класс как раз и используется для построения синтаксических конструкций языков программирования.

Дополнительно следует заметить, что в общем случае подавляющее большинст­во языков программирования (таких, как Pascal, С, FORTRAN и т. п.) формаль­но не являются КС-языками. Причина в том, что в языках программирования всегда присутствует контекстная зависимость, которая выражается, например, в необходимости предварительного описания переменных, в соответствии коли­чества и типов формальных и фактических параметров процедур и функций и т. п. Но с целью упрощения работы компиляторов подобного рода зависимости на этапе синтаксического анализа не учитывают, рассматривая только сами кон­струкции языков программирования, которые формально могут быть описаны с помощью КС-грамматик. Соблюдение контекстных условий (зависимостей) в компиляторах проверяется уже на этапе семантического анализа при подготов­ке к генерации кода.

Лемма о разрастании КС-языков

Лемма о разрастании КС-языков звучит так: если взять достаточно длинную це­почку символов, принадлежащую произвольному КС-языку* то в ней всегда можно выделить две подцепочки, длина которых в сумме больше нуля, таких, что, повторив их сколь угодно большое число раз, можно получить новую цепоч­ку символов, принадлежащую данному языку [6, т. 1].

Формально ее можно определить следующим образом: если L — это КС-язык, то 3 keN, k > 0, что если |а| > к и aeL, то а = еР5ую, где Ру^А., |рбу| < к и ep'Sy'oeL Vi > 0 (где N — это множество целых чисел)¹.

Как и для регулярных языков, лемма о разрастании для КС-языков служит для проверки принадлежности заданного языка классу КС-языков. Доказано, что всякий язык является КС-языком тогда и только тогда, когда для него выполня­ется лемма о разрастании КС-языков.

Например, докажем, что язык L = {aⁿbⁿcⁿ | n > 0} не является КС-языком.

Предположим, что этот язык все же является КС-языком. Тогда для него должна выполняться лемма о разрастании, и существует константа к, заданная в этой лемме. Возьмем цепочку a = a^kb^kc\ |a| > к, принадлежащую этому языку. Если ее записать в виде а = spSyco, то по условиям леммы |р5у| < к, следовательно, цепоч­ка рбу не может содержать вхождений всех трех символов a, b и с — каких-то

Для КС-языков, как и для регулярных языков, с помощью леммы о разрастании можно повторять подцепочки сколько угодно раз и получать новые цепочки языка — исходная цепочка как бы «разрастается» (отсюда название леммы). На самом деле лемма о разрас­тании для КС-языков является частным случаем более общей леммы, известной как «лемма Огдена» [6, т. 1]. символов в ней нет. Рассмотрим цепочку ер°5у°со = ебсо. По условиям леммы она должна принадлежать языку, но в то же время она содержит либо к символов а, либо к символов с и при этом не может содержать к вхождений каждого из сим­волов a, b и с, так как |eSco| < 3k. Значит, какой-то символ в ней встречается мень­ше, чем другие — такая цепочка не может принадлежать языку L. Следовательно, язык L не удовлетворяет требованиям леммы о разрастании КС-языков и поэто­му не является КС-языком.

Преобразование КС-грамматик. Приведенные грамматики

Преобразование грамматик. Цель преобразования

Как было сказано выше, для КС-грамматик невозможно в общем случае прове­рить их однозначность и эквивалентность. Но очень часто правила КС-грамма­тик можно и нужно преобразовать к некоторому заранее заданному виду таким образом, чтобы получить новую грамматику, эквивалентную исходной. Заранее определенный вид правил грамматики позволяет упростить работу с языком, за­данным этой грамматикой, и облегчает создание распознавателей для него.

Таким образом, можно выделить две основные цели преобразований КС-грам­матик: упрощение правил грамматики и облегчение создания распознавателя языка. Не всегда эти две цели можно совместить. В случае с языками програм­мирования, когда итогом работы с грамматикой является создание компилятора языка, именно вторая цель преобразования является основной. Поэтому упро­щениями правил пренебрегают, если при этом удается упростить построение распознавателя языка [12, 15, 32].

Все преобразования условно можно разбить на две группы:

• первая группа — это преобразования, связанные с исключением из граммати­ки тех правил и символов, без которых она может существовать (именно эти преобразования позволяют выполнить основные упрощения правил);

• вторая группа — это преобразования, в результате которых изменяется вид и состав правил грамматики, при этом грамматика может дополняться новыми правилами, а ее словарь нетерминальных символов — новыми символами (то есть преобразования второй группы не связаны с упрощениями).

Следует еще раз подчеркнуть, что всегда в результате преобразований мы полу­чаем новую КС-грамматику, эквивалентную исходной, то есть определяющую тот же самый язык.

Тогда формально преобразование можно определить следующим образом: G(VT,VN,P,S) -» G'(VT^,,Vhf^,,P',S'): L(G) - L(G')

Приведенные грамматики

Приведенные грамматики — это КС-грамматики, которые не содержат недости­жимых и бесплодных символов, циклов и ^.-правил («пустых» правил). Приве­денные грамматики называют также КС-грамматиками в каноническом виде.

Для того чтобы преобразовать произвольную КС-грамматику к приведенному виду, необходимо выполнить следующие действия:

• удалить все бесплодные символы;

• удалить все недостижимые символы;

• удалить ^.-правила;

• удалить цепные правила.

Следует подчеркнуть, что шаги преобразования должны выполняться именно в указанном порядке, и никак иначе.

Удаление недостижимых символов

Символ xe(VTuVN) называется недостижимым, если он не встречается ни в од­ной сентенциальной форме грамматики G(VT,VN,P,S).

Конечно, чтобы исключить из грамматики все недостижимые символы, не надо рассматривать все ее сентенциальные формы (это просто невозможно), доста­точно воспользоваться специальным алгоритмом удаления недостижимых сим­волов.

Алгоритм удаления недостижимых символов строит множество достижимых сим­волов грамматики G(VT,VN,P,S) — Vj. Первоначально в это множество входит только целевой символ грамматики S, затем оно пополняется на основе правил грамматики. Все символы, которые не войдут в данное множество, являются не­достижимыми и могут быть исключены в новой грамматике G' из словаря и из правил.

Алгоритм удаления недостижимых символов по шагам

1. V₀ = {S},i:=l.

2. V; - {х | xe(VTuVN) и (А-хххр)еР, AeV|_„ <x,pe(VTuVN)*} u Vj_₀₁.

3. Если Vj ф Vj.t, то i := i+1 и перейти к шагу 2, иначе перейти к шагу 4.

4. VN' = VN п Vj, VT = VT n Vj, в Р' входят те правила из Р, которые содержат только символы из множества Vj, S' = S.

Удаление бесплодных символов

В грамматике G(VT,VN,P,S) символ AeVN называется бесплодным, если для него выполняется: {а | А=>*а, oieVT} = 0, то есть нетерминальный символ явля­ется бесплодным тогда, когда из него нельзя вывести ни одной цепочки терми­нальных символов.

В простейшем случае символ является бесплодным, если во всех правилах, где этот символ стоит в левой части, он также встречается и в правой части. Более сложные варианты предполагают зависимости между цепочками бесплодных сим­волов, когда они в любой последовательности вывода порождают друг друга.

Для удаления бесплодных символов используется специальный алгоритм удале­ния бесплодных символов. Он работает со специальным множеством нетерми­нальных символов Yj. Первоначально в это множество попадают только те сим­волы, из которых непосредственно можно вывести терминальные цепочки, затем оно пополняется на основе правил грамматики G.

Алгоритм удаления бесплодных символов по шагам

1. Y_o = 0, i:-l.

2. Yj = {А | (А-ж)еР, ae(Y_MuVT)*} u Y_M.

3. Если Yj ф Y_i_₁, то i := i+1 и перейти к шагу 2, иначе перейти к шагу 4.

4. VN' = Yj, VT = VT, в Р' входят те правила из Р, которые содержат только символы из множества (VTuYi), S' = S.

Пример удаления недостижимых и бесплодных символов

Рассмотрим работу алгоритмов удаления недостижимых и бесплодных симво­лов на примере грамматики:

G({a.b,c}.{A,B,C.D.E.F.G.S},P,S)

Р:

S -» аАВ | Е

А -> аА | ЬВ

В -*■ АСЬ | Ь

С -> А | ЬА | сС | аЕ

Е —> сЕ | аЕ J ЕЬ | ED | FG

D -> а | с | Fb

F -> ВС |. ЕС | АС

G -> Ga | Gb

Следует обратить внимание, что для правильного выполнения преобразований необходимо сначала удалить бесплодные символы, а потом — недостижимые сим­волы, но не наоборот. То есть порядок, в каком будут выполняться алгоритмы, имеет существенное значение.

Удалим бесплодные символы:

1. Y_o = 0, i:-l.

2. Y, = {B,D}, Y^Y₀: i:=2.

3. Y₂ = {B,D,A}, Y₂*Y_i: i:=3.

4. Y₃ = {B,D,A,S,C}, Y₃*Y₂: i:=4.

5. Y₄ = {B,D,A,S,C,F}, Y₄*Y₃: i:-5.

6. Y₅ = {B,D,A,S,C,F}, Y₅ = Y₄.

Строим множества VN' = {A,B,C,D,F,S}, VT' - {a,b,c} и Р'.

Получили грамматику:

G'({a.b.c}.{A.B.C.D.F,S}.P',S) P':

S -> aAB A -> aA | bB В -> ACb | b С -> A | bA | cC D -> a | С | Fb F -> ВС | AC

Удалим недостижимые символы:

1. V₀ = {S},i~l.

2. V, = {S,A,B}, V^V₀: i:=2.

3. V₂ = {S,A,B,C}, y>Vj: i:=2.

4. V₃ = {S,A,B,C},V₃ = V₂.

5. Строим множества VN" - {A,B,C,S}, VT" = {a,b,c} и Р'.

В итоге получили грамматику:

G"({a,b.c},{A.B,C.S}.P".S)

Р":

S i* aAB

A -> aA | bB

В -> ACb | b

С -» A | bA | cC Алгоритмы удаления бесплодных и недостижимых символов относятся к первой группе преобразований КС-грамматик. Они всегда ведут к упрощению грамма­тики, сокращению количества символов алфавита и правил грамматики.

Устранение л-правил

^-правилами (или правилами с пустой цепочкой) называются все правила грам­матики вида А->Х, где AeVN.

Грамматика G(VT,VN,P,S) называется грамматикой без ^-правил, если в ней не существует правил (А-»^)еР, A*S и существует только одно правило (S-»^.)eP, в том случае, когда ^eL(G), и при этом S не встречается в правой части ни одно­го правила грамматики.

Для того чтобы упростить построение распознавателей цепочек языка L(G), лю­бую грамматику G целесообразно преобразовать к виду без ^.-правил. Существу­ет алгоритм преобразования произвольной КС-грамматики к виду без ^-правил. Он работает с некоторым множеством нетерминальных символов W;.

Алгоритм устранения - правил по шагам

1. W₀ = {A:(A-^)eP}, i:-l.

2. Wi - W_H u {A: (А-кх)еР, aeW,.,').

3. Если W, ф Wi-ii то i := i+1 и перейти к шагу 2, иначе перейти к шагу 4.

4. VN' = VN, VT' - VT, в Р' входят все правила из Р, кроме правил вида А->\.

5. Если (А-»а)е Р и в цепочку а входят символы из множества Wj, тогда на ос­нове цепочки а строится множество цепочек {а'} путем исключения из а всех возможных комбинаций символов из Wj, и все правила вида А-»а' добавля­ются в Р'.

6. Если SeWj, то значит XeL(G), и тогда в VN' добавляется новый символ S', который становится целевым символом грамматики G, а в Р' добавляются два новых правила: S'-»X,|S; иначе S' = S.

Данный алгоритм часто ведет к увеличению количества правил грамматики, но позволяет упростить построение распознавателя для заданного языка.

Пример устранения - правил

Рассмотрим грамматику:

G({a.b.c}.{A,B.C.S}.P.S)

Р:

S -> АаВ | аВ | сС

А -> АВ | а | b | В

В -> Ва | X

С -> АВ | с

Удалим Х-правила:

1. W₀ = {B},i:=l.

2. W, = {В,А}, W^W₀, i:-2.

3. W₂ = {В,А,С}, W₂*Wi, i:=3.

4. W₃ - {B,A,Q, W₃ = W₂.

5. Построим множества VN' = {A,B,C,S}, VT' я {a,b,c} и множество правил Р'.

6. Рассмотрим все правила из множества Р':

О Из правил S-»AaB | аВ | сС исключим все комбинации А, В и С и получим но­вые правила S—>Аа | аВ j a | a | с, добавим их в Р', исключая дубликаты, полу­чим: S->AaB | аВ | сС | Аа | аВ | а | с.

О Из правил А->АВ | а | b | В исключим все комбинации А и В и получим новые правила A-W\|B, в Р' их добавлять не надо, поскольку правило А-»В там уже есть, а правило А->А бессмысленно.

О Из правила В—>Ва исключим В и получим новое правило В->а, добавим его в Р', получим В->Ва|а.

О Из правил С->АВ | с исключим все комбинации А и В и получим новые пра­вила С—>А| В, добавим их в Р', получим С—>АВ | А | В | с.

7. SeW₃, поэтому в грамматику С не надо добавлять новый целевой символ S', S' = S.

Получим грамматику:

G'({a.b,c}.{A,B.C.S}.P'.S)

Р':

S -> АаВ | аВ | сС | Аа | а | с

А -> АВ | а | b | В

В —> Ва | а

С -> АВ | А | В | с

Устранение цепных правил

Циклом (циклическим выводом) в грамматике G(VT,VN,P,S) называется вывод вида А=>*А, AeVN. Очевидно, что такой вывод абсолютно бесполезен. Поэтому в распознавателях КС-языков целесообразно избегать возможности появления циклов.

Циклы возможны только в том случае, если в КС-грамматике присутствуют цеп­ные правила вида А-»В, А,Ве VN. Чтобы исключить возможность появления цик­лов в цепочках вывода, достаточно устранить цепные правила из набора правил грамматики.

Чтобы устранить цепные правила в КС-грамматике G(VT,VN,P,S), для каждого нетерминального символа XeVN строится специальное множество цепных сим­волов N^x, а затем на основании построенных множеств выполняются преобразо­вания правил Р. Поэтому алгоритм устранения цепных правил надо выполнить для всех нетерминальных символов грамматики из множества VN.

Алгоритм устранения цепных правил по шагам

1. Для всех символов X из множества VN повторять шаги 1-4, затем перейти к шагу 5.

2. NV{X},i:=l.

3. N* = Щ_л и {В: (А->В)еР, Ве№У.

4. Если N^x ф N\i, то i:=i+l и перейти к шагу 2, иначе N^x'= N^-{X} и перейти к шагу 1.

5. VN' = VN, VT = VT, в Р' входят все правила из Р, кроме правил вида А-»В, S' = S.

6. Для всех правил (А-»а)еР', если BeN^A, B*A, то в Р' добавляются правила вида В->а.

Данный алгоритм, так же как и алгоритм устранения А,-правил, ведет к увеличе­нию числа правил грамматики, но упрощает построение распознавателей.

Пример устранения цепных правил

Рассмотрим работу алгоритмов удаления недостижимых и бесплодных симво­лов на примере грамматики:

G({a.b.c}.{A.B.C,S}.P,S)

Р:

S -> АаВ | аВ | сС | Аа | а | с

А —> АВ | а | b | В

В -> Ва | а С —> АВ | А | с

Устраним цепные правила:

1. N^s₀ = {S},i:=l.

2. N^s! = {S}, N^sj= N^s₀, N^s = 0.

3. РП = {А},1:=1.

4. N^A! - {A,B}, NVNV i:-2.

5. N^A₂ = {A,B}, Щ = N^A,, N^A = {B}.

6. N^B₀ = {B},i:=l.

7. N^B! = {B}, N^B,- N^B₀, N^B = 0.

8. N^c₀ = {C},i:=l.

9. N^c, = {C,A}, N^C^N^C₀: i:-2.

10. N^c₂ = {C,A,B}, N^C₂^NS: i:=3.

11. N^c₃ - {C,A,B}, N^c₃ = N^c₂, N^c = {A,B}.

12. Получили: N^s = 0, N^A = {B}, N^B - 0, N^c = {A,B}, S' = S, построим множества VN' = {A,B,C,S}, VT = {a,b,c} и множество правил Р'.

13. Рассмотрим все правила из множества Р' — интерес для нас представляют только правила для символов А и В, так как N^A = {В } и N^c = {А,В}.

О Для правил А-»АВ | а | b имеем новые правила С-»АВ | а | Ь, поскольку Ае№ (пра­вило А-»В цепное и поэтому не входит в Р'), из них правило С-»АВ уже су­ществует в Р'.

О Для правил В-»Ва|а имеем новые правила А-»Ва|а и С—>Ва | а, поскольку BeN^A и BeN^c, из них правила Ан>а и С-»а (последнее добавлено на преды­дущем шаге) уже существуют в Р'.

Получим новую грамматику:

G'({a.b.c}.{A.B.C.S}.P'.S)

Р':

S -> АаВ | аВ | сС | Аа | а | с

А -> АВ | а | b | Ва

В -» Ва | а

С -» АВ | с | а | b | Ва

Рассмотрим дополнительно в качестве примера грамматику для арифметических выражений над символами «а» и «Ь», которая уже рассматривалась ранее в этом пособии в разделе «Проблемы однозначности и эквивалентности грамматик», гла­ва 9 - G({+.-,/.*.a,b}, {S.T.E}, P. S):

Р:

S -> S+T | S-T | Т

Т -> Т*Е | Т/Е | Е

Е -> (S) | а | Ь

Устраним цепные правила:

1. N^s₀ = {S},i:=l.

2. N^s! - {S,T}_; NVN^so, i:-2.

3. N^s₂ = {S,T,E}, ЩфЩ, i:-3.

4. N^S3 = {S₎T,E},N^S3 = NS_2lN^s = {T₁E}.

5. N^T₀ = {T},i:=l.

6. N^T! = {T,E}, NVN^T₀: i:=2.

7. N^T₂ = {T,E}₎N^T₂=N^T₁,N^T = {E}.

8. N^E₀ = {E},i:=l.

9. N^E! = {E}, N^Ej= N^E₀, N^E = 0.

10. Получили: N^s = {T,E}, N^T = {E}, N^E = 0, S' - S, построим множества VN' = {S,T,E}, VT' = {+,-,/,*,a,b } и множество правил Р'.

11. Рассмотрим все правила из множества Р' — интерес представляют только пра­вила для символов Т и Е, так как N^s = {Т,Е} и N^T = {Е}:

О Для правил Т->Т*Е|Т/Е имеем новые правила S->T*E|T/E, поскольку TeN^s.

О Для правил E->(S)|a|b имеем новые правила S-»(S)|a|b и T->(S)|a|b, посколь­ку EeN^s и EeN^T.

Получим новую грамматику:

G'({+.-./.*.a.b}, {S.T.E}. Р'. S) Р';

S -> S+T | S-T | Т*Е | Т/Е | (S) | а | b Т -> Т*Е | Т/Е | (S) | а | b Е -у (S) | а | b

Эту грамматику мы дальше будем использовать для построения распознавателей КС-языков.

КС-грамматики в нормальной форме

Грамматики в нормальной форме Хомского

Нормальная форма Хомского или бинарная нормальная форма (БНФ) — это одна из предопределенных форм для правил КС-грамматики. В нормальную форму Хомского можно преобразовать любую произвольную КС-грамматику. Для пре­образования в нормальную форму Хомского предварительно грамматику надо преобразовать в приведенный вид.

Определение нормальной формы Хомского

КС-грамматика G(VT,VN,P,S) называется грамматикой в нормальной форме Хомского, если в ее множестве правил Р присутствуют только правила следую­щего вида:

1. А -> ВС, где A,B,CeVN.

2. А -» а, где AeVN и aeVT.

3. S -» X, если XeL(G), причем S не должно встречаться в правых частях других правил.

Никакие другие формы правил не должны встречаться среди правил граммати­ки в нормальной форме Хомского [6, т. 1, 26].

КС-грамматика в нормальной форме Хомского называется также грамматикой в бинарной нормальной форме (БНФ). Название «бинарная» происходит от того, что на каждом шаге вывода в такой грамматике один нетерминальный символ может быть заменен только на два других нетерминальных символа. Поэтому в дереве вывода грамматики в нормальной форме Хомского каждая вершина либо распадается на две другие вершины (в соответствии с первым видом правил), либо содержит один последующий лист с терминальным символом (в соответст­вии со вторым видом правил). Третий вид правил введен для того, чтобы к нор­мальной форме Хомского можно было преобразовывать грамматики КС-языков, содержащих пустые цепочки символов.

Алгоритм преобразования грамматики в нормальную форму Хомского

Алгоритм позволяет преобразовать произвольную исходную КС-грамматику в эквивалентную грамматику в нормальной форме Хомского.

Условие: дана КС-грамматика G(VT,VN,P,S), необходимо построить эквивалентную ей грамматику G'(VT,VN',P',S') в нормальной форме Хомского: L(G) = = L(G').

На первом шаге исходную грамматику надо преобразовать к приведенному виду. Поскольку алгоритм преобразования КС-грамматик к приведенному виду был рассмотрен выше, можно считать, что исходная грамматика уже является приве­денной (не содержит бесполезных и недостижимых символов, цепных правил и ^.-правил).

В начале работы алгоритма преобразования приведенной КС-грамматики в нор­мальную форму Хомского множество нетерминальных символов VN' результи­рующей грамматики G' строится на основе множества нетерминальных симво­лов VN исходной грамматики G: VN' = VN.

Затем алгоритм преобразования работает с множеством правил Р исходной грам­матики G. Он просматривает все правила из множества Р и в зависимости от вида каждого правила строит множество правил Р' результирующей граммати­ки G' и дополняет множество нетерминальных символов этой грамматики VN'.

1. Если встречается правило вида А—>а, где AeVN и aeVT, то оно переносится во множество Р' без изменений.

2. Если встречается правило вида А-»ВС, где A,B,CeVN, то оно переносится во множество Р' без изменений.

3. Если встречается правило вида S-^>X, где S — целевой символ грамматики G, тп оно переносится во множество Р' без изменений. Если встречается правило вида А-»аВ, где A.BeVN и aeVT, то во множест­во правил Р' включаются правила А-»<АаВ>В и <АаВ>-»а и новый символ <АаВ > добавляется во множество нетерминальных символов VN' граммати­ки G'.

4. Если встречается правило вида А-»Ва, где A,BeVN и aeVT, то во множество правил Р' включаются правила А-»В<АВа> и <АВа>-»а, и новый символ <АВа> добавляется во множество нетерминальных символов VN' граммати­ки G'.

5. Если встречается правило вида A->ab, где A eVN и a,beVT, то во множество правил Р' включаются правила А-»<Аа><АЬ>, <Аа>-»а и <Ab>->b, новые символы <Аа> и <АЬ> добавляются во множество нетерминальных симво­лов VN' грамматики G'.

6. Если встречается правило вида А-^...Xk, к>2, где AeVN и Vi: X^VTuVN, то во множество правил Р' включается цепочка правил:

А 4 <Х₁'><Х₂...Х_к>

<Х₂...Х_к> -* <Х₂'><Х₃...Х_к>

<Х_ыХ_к> -> <Х_ы'><Х_к'>

новые нетерминальные символы <Х₂...Х_к>, <Х₂...Х_к>,..., <Х_к. Х_к> включают­ся во множество нетерминальных символов VN' грамматики G', кроме того, Vi: если XeVN, то <Xi'>sXi, иначе (если XjeVT) <Xi'> — это новый нетер­минальный символ, он добавляется во множество VN', а во множество пра­вил Р' грамматики G' добавляется правило <Xj'> -> X,.

Целевым символом результирующей грамматики G' является целевой символ исходной грамматики G.

Пример преобразования грамматики в нормальную форму Хомского

Рассмотрим в качестве примера грамматику G({a,b,c},{A,B,C,S},P,S)

Р:

S -* АаВ | Аа | be А —> АВ | а | аС В -> Ва | b ,

С -> АВ | с

Эта грамматика уже находится в приведенной форме. Построим эквивалентную ей грамматику G'(VT,VN',P',S ) в нормальной форме Хомского. Начнем построе­ние с множества нетерминальных символов новой грамматики: VN' = {A,B,C,S}. Множество еще будет дополняться в процессе работы алгоритма.

Начнем разбирать правила этой грамматики.

Первое правило исходной грамматики S-»AaB подпадает под 7-й вариант рабо­ты алгоритма. В соответствии с требованиями алгоритма заменяем его на после­довательность:

S -> <A'><aB> <aB> -j> <a'><B'>

Поскольку А и В — нетерминальные символы, а «а» — терминальный символ, то получаем, что <А'>г=А и <В'>=В, а новое правило <а'>-»а должно быть добав­лено во множество правил Р' новой грамматики. Получаем последовательность правил:

S -> А<аВ> <аВ> -> <а'>В <а' >->а

Во множество нетерминальных символов VN' новой грамматики необходимо до­бавить новые символы <аВ> и <а'>. Получаем VN' = {A,B,C,S,<aB>,<a'>}.

Второе правило исходной грамматики S-»Aa подпадает под 5-й вариант работы алгоритма. Заменяем его на два правила:

S -» A<SAa> <SAa> -> a

Новый символ <SAa> добавляется во множество нетерминальных символов но­вой грамматики. Получаем VN' = {A,B,C,S,<aB>,<a'>,<SAa>}.

Третье правило исходной грамматики S—>Ьс подпадает под 6-й вариант работы алгоритма. Заменяем его на три правила:

S -» <Sb><Sc>

<Sb> -* b <Sc> -> с

Новые символы <Sb> и <Sc> добавляются во множество нетерминальных сим­волов новой грамматики. Получаем VN' = {A,B,C,S,<aB>,<a'>,<SAa>,<Sb>,<Sc>}. Четвертое правило исходной грамматики А->АВ подпадает под 2-й вариант рабо­ты алгоритма. Переносим его во множество правил новой грамматики без изме­нений.

Пятое правило исходной грамматики А-»а подпадает под 1-й вариант работы ал­горитма. Переносим его во множество правил новой грамматики без изменений.

Шестое правило исходной грамматики А-»аС подпадает под 4-й вариант работы алгоритма. Заменяем его на два правила:

А -> <АаОС <АаС> -> а

Новый символ <АаС> добавляется во множество нетерминальных символов но­вой грамматики. Получаем VN' = {A,B,C,S,<aB>,<a'>,<SAa>,<Sb>,<Sc>,<AaC>}.

Седьмое правило исходной грамматики В-»Ва подпадает под 5-й вариант работы алгоритма. Заменяем его на два правила:

В -» В<ВВа> <ВВа> -> а

Новый символ <ВВа> добавляется во множество нетерминальных символов но­вой грамматики. Получаем VN' = {A,B,C,S,<aB>,<a'>,<SAa>,<Sb>,<Sc>,<AaC>, <ВВа>}.

Восьмое правило исходной грамматики В->Ь подпадает под 1-й вариант работы алгоритма. Переносим его во множество правил новой грамматики без изменений.

Девятое правило исходной грамматики С-»АВ подпадает под 2-й вариант работы алгоритма. Переносим его во множество правил новой грамматики без изменений.

Десятое правило исходной грамматики С-»с подпадает под 1-й вариант работы алгоритма. Переносим его во множество правил новой грамматики без изменений.

Рассмотрение множества правил исходной грамматики закончено. Множестве правил Р' новой грамматики G' и множество нетерминальных символов VN этой грамматики окончательно построены. Целевым символом новой граммати­ки является символ S.

Получаем новую грамматику в нормальной форме Хомского, эквивалентную ис­ходной: G4{a,b,с} ,{А,В,С,S,<aB>,<a4<SAa>,<Sb>,<Sc>,<AaC>,<BBa>},P\S)^

Р':

S -> А<аВ> | A<SAa> | <Sb><Sc>

<аВ> -4 <а'>В

<а'>-»а

<SAa> -* a

<Sb> --» b

<Sc> -> с

А —> АВ | а | <АаОС

<АаС> -> а

В -» В<ВВа> | b

<ВВа> -> а

С —> АВ | с Видно, что при приведении грамматики к нормальной форме Хомского количе ство правил и нетерминальных символов в грамматике увеличивается. При этом растет объем грамматики и несколько затрудняется ее восприятие человеком. Од нако цель преобразования — не упрощение грамматики, а упрощение построе ния распознавателя языка на ее основе. Именно этой цели и служит нормальна форма Хомского. Далее будут рассмотрены методы построения распознавателей в основе которых лежит именно эта форма представления грамматики КС языка.

Устранение левой рекурсии. Грамматики в нормальной форме Грейбах

Определение левой рекурсии

Символ AeVN в КС-грамматике G(VT,VN,P,S) называется рекурсивным, есл для него существует цепочка вывода вида А=>+аА(3, где a,pe(VTuVN)*.

Если а = X и $*\, то рекурсия называется левой, а грамматика G — леворекурсивной; если а*Х и (3 = X, то рекурсия называется правой, а грамматика G — прг ворекурсивной. Если a = X и р = X, то рекурсия представляет собой цикл. Котр грамматика G — приведенная, в ней нет цепных правил и не может встречатьс циклов, поэтому далее циклы рассматриваться не будут.

Любая КС-грамматика может быть как леворекурсивной, так и праворекурсивной, а также леворекурсивной и праворекурсивной одновременно (по различ­ным символам из множества нетерминальных символов).

КС-грамматика называется нелеворекурсивной, если она не является леворекур­сивной. Аналогично, КС-грамматика является неправорекурсивной, если не яв­ляется праворекурсивной.

Некоторые алгоритмы левостороннего разбора для КС-языков не работают с ле­ворекурсивными грамматиками, поэтому возникает необходимость исключить левую рекурсию из выводов грамматики. Далее будет рассмотрен алгоритм, ко­торый позволяет преобразовать правила произвольной КС-грамматики таким образом, чтобы в выводах не встречалась левая рекурсия.

Следует отметить, что поскольку рекурсия лежит в основе построения языков на основе правил грамматики в форме Бэкуса—Наура, полностью исключить рекур­сию из выводов грамматики невозможно. Можно избавиться только от одного вида рекурсии — левого или правого, то есть преобразовать исходную граммати­ку G к одному из видов: нелеворекурсивному (избавиться от левой рекурсии) или неправорекурсивному (избавиться от правой рекурсии). Для левосторонних распознавателей интерес представляет избавление от левой рекурсии — то есть преобразование грамматики к нелеворекурсивному виду.

Доказано, что любую КС-грамматику можно преобразовать к нелеворекурсивно­му или неправорекурсивному виду.

Алгоритм устранения левой рекурсии

Условие: дана КС-грамматика G(VT,VN,P,S), необходимо построить эквивалент­ную ей нелеворекурсивную грамматику G'(VN',VT,P',S'): L(G) = L(G').

Алгоритм преобразования работает с множеством правил исходной граммати-¹ ки Р, множеством нетерминальных символов VN и двумя переменными счетчи­ками: i и j.

Шаг 1. Обозначим нетерминальные символы грамматики так: VN = {А!,А₂,...,А_П}. i:= 1.

Шаг 2. Рассмотрим правила для символа А;. Если эти правила не содержат левой рекурсии, то перенесем их во множество правил Р' без изменений, а символ Aj добавим во множество нетерминальных символов VN'.

Иначе запишем правила для Aj в виде А, -» A_iai|A_ia₂|...|A_iaJpi|P2l-|Pp. где Vj 1 < j < Р ни одна из цепочек Pj не начинается с символов А_к, таких, что k < i.

Вместо этого правила во множество Р' запишем два правила вида:

А^ —»a₁|a₂|...|aJa₁A_i'|a2A_i'|...|a_mA_i'

Символы Aj и А_;' включаем во множество VN'.

Теперь все правила для А; начинаются либо с терминального символа, либо с не­терминального символа Ак, такого, что k > i. Шаг 3. Если i = п, то грамматика G' построена, иначе i := i+1, j := 1 и перейти к шагу 4.

Шаг 4. Для символа Aj во множестве правил Р' заменить все правила вида А;-»Аа, где ae(VTuVN)*, на правила вида А^р^Рзоф.^Рща, причем Aj—>Pi|p2l---lP_m — все правила для символа Aj.

Так как правая часть правил Aj-»p₁|p₂|...|p_m уже начинается с терминального сим­вола или нетерминального символа А_к, к > j, то и правая часть правил для симво­ла Aj будет удовлетворять этому условию.

Шаг 5. Если j = i-1, то перейти к шагу 2, иначе j := j+1 и перейти к шагу 4.

Шаг 6. Целевым символом грамматики G' становится символ А_к, соответствую­щий символу S исходной грамматики G.

Рассмотрим в качестве примера грамматику для арифметических выражений над символами «а» и «b» G({+,-,/,*,a,b}, {S,T,E}, P, S):

Р:

S -> S+T | S-T | Т

Т -> Т*Е | Т/Е | Е

Е -4 (S) | а | b

Эта грамматика является леворекурсивной. Построим эквивалентную ей нелево­рекурсивную грамматику G'.

Шаг 1. Обозначим VN - {A_h A₂, A₃}. i .:= 1,

Тогда правила грамматики G будут иметь вид:

Aj -> A_t+A₂ | А_ГА₂ | А₂

А₂ -> А₂*А₃ | А₂/А₃ | А₃

А₃ -> (Aj) | а | Ь

Шаг 2. Для А! имеем правила А₁->А₁+А₂|А₁-А₂|А₂. Их можно записать в виде A_t-> —>А₁сх₁1 A₍a₂1 р₁₍ где Щ = + А₂, a₂ = -A₂, P_t = A₂.

Запишем новые правила для множества Р':

Aj -» А₂|А₂А_1;'

A,i' -> +А₂| -A₂|+A₂Ai' j-AvjAi'

Добавив эти правила в Р', а символы Aj и А{ во множество нетерминальных

символов, получим: VN' = {А₁₍АГ}-

Шаг 3. i = 1 < 3. Построение не закончено: i := i+1 = 2, j := 1.

Шаг 4. Для символа А₂ во множестве правил Р' нет правила вида А₂->А₁а, поэто­му на этом шаге никаких действий не выполняем.

Шаг 5. j = 1 = i-1, переходим опять к шагу 2.

Шаг 2. Для А₂ имеем правила А₂->А₂*А₃1A2/A31А₃. Их можно записать в виде А₂-» -^А₂а, | А₂а₂1 р_1; где сц = *А₃, а₂ = /A3. Pi ⁼ А₃. Запишем новые правила для множества Р':

А₂ -> А₃1А₃А₂"

А₂: -> *А₃1 /А₃1 *А₃А₂ ■ [ /А₃А₂'

Добавим эти правила в Р', а символы А₂ и А₂' во множество нетерминальных символов, получим: VN' = {А^А/.А^А^}.

Шаг j?. i = 2 < 3. Построение не закончено: i := i+1 = 3, j := 1.

Шаг 4. Для символа А₃ во множестве правил Р' нет правила вида Аз-^а, поэто­му на этом шаге никаких действий не выполняем.

Шаг 5. j = 1 < i-1, j := j+1 = 2, переходим к шагу 4.

Шаг 4. Для символа А₃ во множестве правил Р' нет правила вида А₃-»А₂а, поэто­му на этом шаге никаких действий не выполняем.

Шаг 5. j = 2 = i-1, переходим опять к шагу 2.

Шаг 2. Для А₃ имеем правила А₃ -> (А,) | а | Ь. Эти правила не содержат левой рекурсии. Переносим их в Р', а символ А₃ добавляем в VN'. Получим: VN' = =s {A^Aj ,A₂,A2 ,A₃}.

Шаг 3. i = 3 = 3. Построение грамматики G' закончено.

В результате выполнения алгоритма преобразования получили нелеворекурсив­ную грамматику G({+,-./.*,a,b}, {A_t.Aj' ,А₂,А₂' ,А₃}, Р', A_t) с правилами:

Р':

А, -» А₂ | A₂A_t'

Aj' -> +А₂ | -А₂ | +А₂А,' | -А₂А('

А₂ -> А₃ | А₃А₂'

V -> *А₃ | /Аз | *А₃А₂' | /А₃А₂'

А₃ -> (Aj) | а | b

Грамматики в нормальной форме Грейбах

На основании грамматики, в которой исключена левая рекурсия, можно постро­ить грамматику в нормальной форме Грейбах.

КС-грамматика G(VT,VN,P,S) называется грамматикой в нормальной форме Грей­бах, если она не является леворекурсивной и в ее множестве правил Р присутст­вуют только правила следующего вида:

1. А -> аа, где aeVT и aeVN*.

2. S -» X, если ^eL(G), причем S не должно встречаться в правых частях других правил.

Никакие другие формы правил не должны встречаться среди правил граммати­ки в нормальной форме Грейбах.

Нормальная форма Грейбах является удобной формой представления грамматик для построения нисходящих левосторонних распознавателей (в тех случаях, ко­гда присутствие левой рекурсии в правилах грамматики недопустимо). В данном пособии эта нормальная форма отдельно не рассматривается. Подробнее с нею можно ознакомиться в [6, т. 1, 26].

Распознаватели КС-языков с возвратом

Принципы работы распознавателей с возвратом

Распознаватели с возвратом — это самый примитивный тип распознавателей для КС-языков. Логика их работы основана на моделировании недетерминированно­го МП-автомата.

Поскольку моделируется недетерминированный МП-автомат (который в общем виде не преобразуется в детерминированный), то на некотором шаге работы мо­делирующего алгоритма возможно возникновение нескольких допустимых сле­дующих состояний автомата. В таком случае существуют два варианта реализа­ции алгоритма [6, т. 1, 40].

В первом варианте на каждом шаге работы алгоритм должен запоминать все воз­можные следующие состояния МП-автомата, выбирать одно из них, переходить в это состояние и действовать так до тех пор, пока либо не будет достигнуто ко­нечное состояние автомата, либо автомат не перейдет в такую конфигурацию, когда следующее состояние будет не определено. Если достигнуто одно из ко­нечных состояний — входная цепочка принята, работа алгоритма завершается. В противном случае алгоритм должен вернуть автомат на несколько шагов на­зад, когда еще был возможен выбор одного из набора следующих состояний, вы­брать другой вариант и промоделировать поведение автомата с этим условием. Алгоритм завершается с ошибкой, когда все возможные варианты работы авто­мата будут перебраны и ни одно из возможных конечных состояний не было достигнуто.

Во втором варианте алгоритм моделирования МП-автомата должен на каждом шаге работы при возникновении неоднозначности с несколькими возможными следующими состояниями автомата запускать новую свою копию для обработки каждого из этих состояний. Алгоритм завершается, если хотя бы одна из выпол­няющихся его копий достигнет одно из конечных состояний. При этом работа всех остальных копий алгоритма прекращается. Если ни одна из копий алгорит­ма не достигла конечного состояния МП-автомата, то алгоритм завершается с ошибкой.

Второй вариант реализации алгоритма связан с управлением параллельными процессами в вычислительных системах, поэтому сложен в реализации. Кроме того, на каждом шаге работы МП-автомата альтернатив следующих состояний может быть много, а количество возможных параллельно выполняющихся про­цессов в операционных системах ограничено, поэтому применение второго ва­рианта алгоритма осложнено. По этим причинам большее распространение по­лучил первый вариант алгоритма, который предусматривает возврат к ранее запомненным состояниям МП-автомата — отсюда и название «разбор с возвра­тами». Следует отметить, что, хотя МП-автомат является односторонним распознавате­лем, алгоритм моделирования его работы предусматривает возврат назад, к уже прочитанной части цепочки символов, чтобы исключить недетерминизм в пове­дении автомата (который невозможно промоделировать).

Есть еще одна особенность в моделировании МП-автомата: любой практически ценный алгоритм должен завершаться за конечное число шагов (успешно или неуспешно). Алгоритм моделирования работы произвольного МП-автомата в об­щем случае не удовлетворяет этому условию. Например, даже после считывания всей входной цепочки символов МП-автомат может совершить произвольное (в том числе и бесконечное) число переходов. В том случае, если цепочка не принята, это может привести к бесконечному количеству шагов моделирующего алгоритма, который по этой причине никогда не будет закончен.

Чтобы избежать таких ситуаций, алгоритмы разбора с возвратами строят не для произвольных МП-автоматов, а для МП-автоматов, удовлетворяющим некото­рым заданным условиям. Как правило, эти условия связаны с тем, что МП-авто­мат должен строиться на основе грамматики заданного языка только после того, как она подвергнется некоторым преобразованиям. Поскольку преобразования грамматик сами по себе не накладывают каких-либо ограничений на входной класс КС-языков (в результате преобразования мы всегда получаем эквивалент­ную грамматику), то они и не ограничивают применимости алгоритмов разбора с возвратами — эти алгоритмы применимы для любого КС-языка, заданного произвольной КС-грамматикой или МП-автоматом.

Алгоритмы разбора с возвратами обладают экспоненциальными характеристика­ми. Это значит, что вычислительные затраты алгоритмов экспоненциально зави­сят от длины входной цепочки символов: a, aeVT, n = |а|. Конкретная зависи­мость определяется вариантом реализации алгоритма.

Доказано, что в общем случае при первом варианте реализации для произволь­ной КС-грамматики G(VT,VN,P,S) время выполнения данного алгоритма Т_э бу­дет иметь экспоненциальную зависимость от длины входной цепочки, а необхо­димый объем памяти М_э — линейную зависимость от длины входной цепочки: Т_э = 0(е^п) и М_э = О(п). При втором варианте реализации, наоборот, время вы­полнения данного алгоритма Т_э будет иметь линейную зависимость от длины входной цепочки, а необходимый объем памяти М_э — экспоненциальную зависи­мость от длины входной цепочки: Т_э = О(п) и М_э = 0(е^п).

Экспоненциальная зависимость вычислительных затрат от длины входной це­почки существенно ограничивает применимость алгоритмов разбора с возврата­ми. Они тривиальны в реализации, но имеют неудовлетворительные характери­стики, поэтому могут использоваться только для простых КС-языков с малой длиной входных предложений языка¹. Для многих классов КС-языков существу-

Возможность использовать эти алгоритмы в реальных компиляторах весьма сомнитель­на, поскольку длина входной цепочки может достигать нескольких тысяч и даже десят­ков тысяч символов. Очевидно, что время работы алгоритма при экспоненциальной зависимости требуемых вычислительных ресурсов от длины входной цепочки символов будет в таком варианте явно неприемлемым даже на самых современных компьютерах. ют более эффективные алгоритмы распознавания, поэтому алгоритмы разбор; с возвратами применяются редко.

Далее рассмотрены два основных варианта таких алгоритмов.

Нисходящий распознаватель с возвратом

Принцип работы нисходящего распознавателя с подбором альтернатив

Этот распознаватель моделирует работу МП-автомата с одним состояние\ q: R({q}, V,Z,5,q,S,{q}). Автомат распознает цепочки КС-языка, заданного КС грамматикой G(VT,VN,P,S). Входной алфавит автомата содержит терминальны! символы грамматики: V = VT, а алфавит магазинных символов строится из тер минальных и нетерминальных символов грамматики: Z = VTuVN.

Начальная конфигурация автомата определяется так: (q,a,S) — автомат пребы вает в своем единственном состоянии q, считывающая головка находится в нача ле входной цепочки символов aeVT*, в стеке лежит символ, соответствующие целевому символу грамматики S.

Конечная конфигурация автомата определяется так: (q,X,X) — автомат пребывае^-в своем единственном состоянии q, считывающая головка находится за концов входной цепочки символов, стек пуст.

Функция переходов МП-автомата строится на основе правил грамматики:

1. (q,a)e8(q,A.,A), AeVN, ae(VTuVN)*, если правило A->a содержится во мно жестве правил Р грамматики G: A-»a e Р.

2. (q,X,)eS(q,a,a) VaeVT.

Этот МП-автомат уже был рассмотрен выше.

Работу данного МП-автомата можно неформально описать следующим образом если на верхушке стека автомата находится нетерминальный символ А, то еп можно заменить на цепочку символов а, если в грамматике языка есть правил! А—>а, не сдвигая при этом считывающую головку автомата (этот шаг работы на зывается «подбор альтернативы»); если же на верхушке стека находится терми нальный символ а, который совпадает с текущим символом входной цепочки, п этот символ можно выбросить из стека и передвинуть считывающую головку н; одну позицию вправо (этот шаг работы называется «выброс»). Данный МП-ав томат может быть недетерминированным, поскольку при подборе альтернатив! в грамматике языка может оказаться более одного правила вида А-»сс, следо вательно, тогда функция 8(q,A.,A) будет содержать более одного следующего со стояния — у автомата будет несколько альтернатив.

Данный МП-автомат строит левосторонние выводы для грамматики G(VT,Vr> P,S). Для моделирования такого автомата необходимо, чтобы грамматика G(VT VN,P,S) не была леворекурсивной (в противном случае, очевидно, автомат мо жет войти в бесконечный цикл). Поскольку, как было доказано выше, произволь ную КС-грамматику всегда можно преобразовать к нелеворекурсивному виду, т этот алгоритм применим для любой КС-грамматики, следовательно, им мож» распознавать цепочки любого КС-языка. Рассмотренный МП-автомат строит левосторонние выводы и читает цепочку входных символов слева направо. Поэтому для него естественным является по­строение дерева вывода сверху вниз. Такой распознаватель называется нисходя­щим.

Решение о том, выполнять ли на каждом шаге работы МП-автомата выброс или подбор альтернативы, принимается однозначно. Моделирующий алгоритм дол­жен обеспечивать выбор одной из возможных альтернатив и хранение информа­ции о том, какие альтернативы на каком шаге уже были выбраны, чтобы иметь возможность вернуться к этому шагу и подобрать другие альтернативы. Такой алгоритм разбора называется алгоритмом с подбором альтернатив.

Реализация алгоритма распознавателя с подбором альтернатив

Существует масса способов реализации алгоритма, моделирующего работу этого МП-автомата. Рассмотрим один из примеров реализации алгоритма нисходяще­го распознавателя с возвратом.

Для работы алгоритма используется МП-автомат, построенный на основе исход­ной грамматики G(VT,VN,P,S). Для удобства работы все правила из множест­ва Р в грамматике G представим в виде A-»ai|a₂|.:.|et_nj то есть пронумеруем все возможные альтернативы для каждого нетерминального символа AeVN. Вход­ная цепочка символов имеет вид a = а₁а₂...а_п, |а| = п. В алгоритме используется также еще дополнительное состояние автомата b (от «back» — «назад»), которое сигнализирует о выполнении возврата к уже прочитанной части входной цепоч­ки¹. Для хранения уже выбранных альтернатив используется дополнительный стек L₂, который может содержать следующую информацию:

• символы aeVT входного языка автомата;

• символы вида Aj, где AeVN — это означает, что среди всех возможных правил для символа А была выбрана альтернатива с номером j.

В итоге алгоритм работает с двумя стеками: L_t — стек МП-автомата и L₂ — стек возвратов. Оба они представлены в виде цепочек символов. Символы в цепочку стека L_t помещаются слева, а в цепочку стека L₂ — справа. В целом состояние ал­горитма на каждом шаге определяется четырьмя параметрами: (Q, i, L_b L₂), где Q — текущее состояние автомата (q или b); i — положение считывающей голов­ки во входной цепочке символов а (1 < i < n+1); L_t — содержимое стека МП-ав­томата; L₂ — содержимое дополнительного стека.

Начальным состоянием алгоритма является состояние (q, 1, S, X), где S — целе­вой символ грамматики. Алгоритм начинает свою работу с начального состояния и циклически выполняет шесть шагов до тех пор, пока не перейдет в конечное состояние или не обнаружит ошибку. На каждом шаге алгоритма проверяется,

Сам автомат имеет только одно состояние q, которого достаточно для его функциониро­вания, однако нет возможности моделировать на компьютере работу недетерминирован­ного автомата, поэтому приходится выполнять возврат к уже прочитанной части цепочки и вводить для этой цели дополнительное состояние.

соответствует ли текущее состояние алгоритма заданному для данного шага и< ходному состоянию, и выполняются ли заданные дополнительные условия. Есл это требование выполняется, алгоритм переходит в следующее состояние, уст; новленное для этого шага, если нет — шаг пропускается, алгоритм переходит следующему шагу.

Алгоритм предусматривает циклическое выполнение следующих шагов.

Шаг 1 (Разрастание), (q, i, Ар, а) ->■ (q, i, уф, аА^, если A-»Yi — это первая i всех возможных альтернатив для символа А.

Шаг 2 (Успешное сравнение), (q, i, ар, а) -> (q, i+1, Р, аа), если а = a_i? aeVT.

ШагЗ (Завершение). Если состояние соответствует (q, п+1Д, а), то разбор заве' шен, алгоритм заканчивает работу, иначе (q, i, X, а) -» (b, i, X, а), когда i*n+l.

Шаг 4 (Неуспешное сравнение), (q, i, ар, а) -> (b, i, ap, а), если а Ф a;, aeVT.

Шаг 5 (Возврат по входу), (b, i, Р, аа) -> (q, i-1, ар, а), V aeVT.

Шаг 6 (Другая альтернатива). Исходное состояние (b, i, Yjp, aAj), действия:

О перейти в состояние (q, i, Yj+tP> otAj₊₁), если еще существует альтерната: A—>Yj₊₁ для символа AeVN;

О сигнализировать об ошибке и прекратить выполнение алгоритма, если А= и не существует больше альтернатив для символа S;

О иначе перейти в состояние (q, i, Ap, a).

В случае успешного завершения алгоритма цепочку вывода можно построить основе содержимого стека L₂, полученного в результате выполнения алгорит\ Цепочка вывода строится следующим образом: поместить в цепочку номер пр вила т, соответствующий альтернативе А—»у|, если в стеке содержится симв> Aj^-, все символы aeVT, содержащиеся в стеке L₂, игнорируются.

Этот алгоритм может быть напрямую использован для построения распознаг телей. Следует помнить, что для применения этого алгоритма исходная гра матика не должна быть леворекурсивной. Если это условие не удовлетворяв ся, то грамматику предварительно надо преобразовать к нелеворекурсивному виду.

Рассмотрим в качестве примера грамматику G({+,-,/,*,а,b}, {S,R,T,F,E}, P,

с правилами:

Р:

S -» Т | TR

R _> +т | -Т | +TR | -TR

Т -> Е | EF

F -> *Е | /Е | *EF | /EF

Е -» (S) | a | b

Это нелеворекурсивная грамматика для арифметических выражений (pai в разделе «Устранение левой рекурсии. Грамматики в нормальной фор Грейбах» она была построена с помощью алгоритма устранения левой ] курсии).

На основании полученной цепочки номеров альтернатив

SjTtEsRjTiEjSiTaEiFtEa

построим последовательность номеров примененных правил: 2, 7, 14, 3, 7, 13, 1, 8, 14, 9, 15. Получаем левосторонний вывод: S => TR => ER => aR => а+Т => а+Е ^> a+(S) => а+(Т) Щ a+(EF) => a+(a'F) => a+(a*E) => a+(a*b). Соответствующее ему дерево вывода приведено на рис. 11.2.

Рис. 11.2. Дерево вывода для грамматики без левых рекурсий

Из приведенного примера очевиден недостаток алгоритма нисходящего разбора с возвратами — значительная временная емкость: для разбора достаточно корот­кой входной цепочки (всего 7 символов) потребовалось 68 шагов работы алго­ритма. Такого результата и следовало ожидать, исходя из экспоненциальной зависимости необходимых для работы алгоритма вычислительных ресурсов от длины входной цепочки. Это существенный недостаток данного алгоритма. Преимуществом данного алгоритма можно считать простоту его реализации. Прак­тически этот алгоритм разбора можно использовать только тогда, когда извест­но, что длина исходной цепочки символов заведомо не будет большой (не боль­ше нескольких десятков символов). Для реальных компиляторов такое условие невыполнимо, но для некоторых небольших распознавателей вполне допустимо, и здесь данный алгоритм разбора может найти применение именно благодаря своей простоте.

Еще одно преимущество алгоритма — его универсальность. На его основе можно распознавать входные цепочки языка, заданного любой КС-грамматикой, доста­точно лишь привести ее к нелеворекурсивному виду (а это можно сделать с любой грамматикой, см. раздел «Преобразование КС-грамматик. Приведенные грамма­тики»). Интересно, что грамматика даже не обязательно должна быть однознач-

ной — для неоднозначной грамматики алгоритм найдет один из возможных ле­восторонних выводов.

Сам по себе алгоритм разбора с подбором альтернатив, использующий возвраты, не находит применения в реальных компиляторах. Однако его основные принци­пы лежат в основе многих нисходящих распознавателей, строящих левосторон­ние выводы и работающих без использования возвратов. Методы, позволяющие строить такие распознаватели для некоторых классов КС-языков, рассмотрены далее. Эти распознаватели будут более эффективны в смысле необходимых вы­числительных ресурсов, но алгоритмы их работы уже более сложны, кроме того, они не являются универсальными.

Распознаватель на основе алгоритма «сдвиг-свертка»

Принцип работы восходящего распознавателя по алгоритму «сдвиг-свертка»

Этот распознаватель строится на основе расширенного МП-автомата с одним состоянием q: R({q},V,Z,5,q,S,{q}). Автомат распознает цепочки КС-языка, задан­ного КС-грамматикой G(VT,VN,P,S). Входной алфавит автомата содержит тер­минальные символы грамматики: V = VT; а алфавит магазинных символов стро­ится из терминальных и нетерминальных символов грамматики: Z = VTuVN.

Начальная конфигурация автомата определяется так: (q,a,X) — автомат пребыва­ет в своем единственном состоянии q, считывающая головка находится в начале входной цепочки символов aeVT", стек пуст.

Конечная конфигурация автомата определяется так: (q,X,S) — автомат пребывает в своем единственном состоянии q, считывающая головка находится за концом входной цепочки символов, в стеке лежит символ, соответствующий целевому символу грамматики S.

Функция переходов МП-автомата строится на основе правил грамматики:

1. (q,A)e8(q,^,y), AeVN, ye(VTuVN)*, если правило А-»у содержится во мно­жестве правил Р грамматики G: А->у е Р.

2. (q,a)e5(q,a,A.) VaeVT.

Неформально работу этого расширенного автомата можно описать так: если на верхушке стека находится цепочка символов у, то ее можно заменить на нетер­минальный символ А, если в грамматике языка существует правило вида А-»у, не сдвигая при этом считывающую головку автомата (этот шаг работы называет­ся «свертка»); с другой стороны, если считывающая головка автомата обозревает некоторый символ входной цепочки а, то его можно поместить в стек, сдвинув при этом головку на одну позицию вправо (этот шаг работы называется «сдвиг» или «перенос»). Сам алгоритм, моделирующий работу такого расширенного ав­томата, называется алгоритмом «сдвиг-свертка» или «перенос-свертка» (по на­званиям основных действий алгоритма).

Данный расширенный МП-автомат строит правосторонние выводы для грам­матики G(VT,VN,P,S). Для моделирования такого автомата необходимо, чтобы грамматика G(VT,VN,P,S) не содержала ^.-правил и цепных правил (в против­ном случае, очевидно, автомат может войти в бесконечный цикл из сверток). По­скольку, как было доказано выше, произвольную КС-грамматику всегда можно преобразовать к виду без ^.-правил и цепных правил, то этот алгоритм применим для любой КС-грамматики, следовательно, им можно распознавать цепочки любого КС-языка.

Этот расширенный МП-автомат строит правосторонние выводы и читает цепоч­ку входных символов слева направо. Поэтому для него естественным является построение дерева вывода снизу вверх. Такой распознаватель называется восхо­дящим.

Данный расширенный МП-автомат потенциально имеет больше неоднозначно­стей, чем рассмотренный ваше МП-автомат, основанный на алгоритме подбора альтернатив. На каждом шаге работы автомата надо решать следующие вопросы:

• что необходимо выполнять: сдвиг или свертку;

• если выполнять свертку, то какую цепочку у выбрать для поиска правил (це­почка у должна встречаться в правой части правил грамматики);

• какое правило выбрать для свертки, если окажется, что существует несколько правил вида А-»у (несколько правил с одинаковой правой частью).

Чтобы промоделировать работу этого расширенного МП-автомата, надо на каж­дом шаге запоминать все предпринятые действия, чтобы иметь возможность вер­нуться к уже сделанному шагу и выполнить эти же действия по-другому. Этот процесс должен повторяться до тех пор, пока не будут перебраны все возможные варианты.

Реализация распознавателя с возвратами на основе алгоритма «сдвиг-свертка»

Существует несколько реализаций для алгоритма моделирования работы такого расширенного МП-автомата [6, т. 1, 40]. Один из вариантов рассмотрен ниже.

Для работы алгоритма всем правилам грамматики G(VT,VN,P,S ), на основе ко­торой построен автомат, необходимо дать порядковые номера. Будем нумеровать правила грамматики в направлении слева направо и сверху вниз в порядке их за­писи в форме Бэкуса—Наура. Входная цепочка символов имеет вид а = aia₂...a_n,

|а| = п.

Алгоритм моделирования расширенного МП-автомата, аналогично алгоритму нисходящего распознавателя, использует дополнительное состояние b и допол­нительный стек возвратов L₂. В стек помещаются номера правил грамматики, использованных для свертки, если на очередном шаге алгоритма была выполне­на свертка, или 0, если на очередном шаге алгоритма был выполнен сдвиг.

В итоге алгоритм работает с двумя стеками: L] — стек МП-автомата и L₂ — стек возвратов. Первый представлен в виде цепочки символов, второй — цепочки це­лых чисел от 0 до т, где т — количество правил грамматики G. Символы в це- почку стека Li помещаются справа, числа в стек L₂ — слева. В целом состояние алгоритма на каждом шаге определяется четырьмя параметрами: (Q, i, L,, L₂), где Q. — текущее состояние автомата (q или b); i — положение считывающей го­ловки во входной цепочке символов а (К i < n+1); Lj - содержимое стека МП-автомата; L₂ — содержимое дополнительного стека возвратов.

Начальным состоянием алгоритма является состояние (q, 1, X, X). Алгоритм

начинает свою работу с начального состояния и циклически выполняет пят!

шагов до тех пор, пока не перейдет в конечное состояние или не обнаружш

ошибку.

Алгоритм предусматривает циклическое выполнение следующих шагов.

Шаг 1 (Попытка свертки), (q, i, ар, у) ->• (q, i, аА, jy), если А-»Р - это первое и:

всех возможных правил из множества правил Р с номером j для подцепочки р

причем оно есть первое подходящее правило для цепочки ар, для которой пра

вило вида А-»р существует. Если удалось выполнить свертку — возвращаемся i

шагу 1, иначе — переходим к шагу 2.

Шаг 2 (Перенос - сдвиг). Если i<n+l, то (q, i, а, у) -> (q, i+1, аг_ь Оу), a, eVT

Если i = n+1, то перейти к шагу 3, иначе перейти к шагу 1.

Шаг 3 (Завершение). Если состояние соответствует (q, n+1, S, у), то разбор завер

шен, алгоритм заканчивает работу, иначе перейти к шагу 4.

Шаг 4 (Переход к возврату), (q, n+1, а, у) -» (Ь, п+1, а, у). Шаг 5 (Возврат). Если исходное состояние (b, i, аА, jy), то:

О перейти в состояние (q, i, а'В, ky), если j > 0, и А-»Р - это правило с номе ром j и существует правило В->Р' с номером к, к > j, такое, что ар = а'Р после чего надо вернуться к шагу 1;

О перейти в состояние (Ь, п+1, ар, у), если i = n+1, j > 0, А->Р - это правил с номером j и не существует других правил из множества Р с номеро: k > j, таких, что их правая часть является правой подцепочкой из цепочк ар; после этого вернуться к шагу 5;

О перейти в состояние (q, i+1, ар^, Оу), aj eVT, если i * n+1, j > 0, A->P - эт правило с номером j и не существует других правил из множества Р с^нс мером k>j, таких, что их правая часть является правой подцепочкой у цепочки аР; после этого перейти к шагу 1;

О иначе сигнализировать об ошибке и прекратить выполнение алгоритма.

Если исходное состояние (b, i, аа, Оу), a eVT, то если i > 1, тогда перейти в cm

дующее состояние (b, i-1, а, у) и вернуться к шагу 5; иначе сигнализировать с

ошибке и прекратить выполнение алгоритма.

В случае успешного завершения алгоритма цепочку вывода можно построить i

основе содержимого стека L₂, полученного в результате выполнения алгоритм

Для этого достаточно удалить из стека L₂ все цифры 0 — и получим последов

тельность номеров правил.

Этот алгоритм может быть напрямую использован для построения распознав

телей. Следует помнить, что для применения этого алгоритма исходная грамм

тика не должна допускать циклов и не должна содержать ^-правил. Если это ус­ловие не удовлетворяется, то грамматику надо предварительно преобразовать к приведенной форме.

Возьмем в качестве примера грамматику G({+,-,/,*,а,b}, {S.T.E}, P, S):

Р:

S -> S+T | S-T | Т*Е | Т/Е | (S) | а | b

Т -» Т*Е | Т/Е | (S) | а | b

Е 4 (S) | а | b

Это грамматика для арифметических выражений, в которой устранены цепные правила (ее уже рассматривали в разделе «Преобразование КС-грамматик. При­веденные грамматики»). Следовательно, в ней не может быть циклов¹. Кроме того, видно, что в ней нет ^.-правил. Таким образом, цепочки языка, заданного этой грамматикой, можно распознавать с помощью алгоритма восходящего распозна­вателя с возвратами.

Проследим разбор цепочки а+(а*Ь) из языка этой грамматики. Работу алгоритма будем представлять в виде последовательности его состояний, взятых в скобки {} (фигурные скобки используются, чтобы не путать их с круглыми скобками, пре­дусмотренными в правилах грамматики). Правила будем нумеровать слева на­право и сверху вниз (всего в грамматике получается 15 правил). Для пояснения каждый шаг работы сопровождается номером шага алгоритма, который был при­менен для перехода в очередное состояние (записывается перед состоянием че­рез символ : — двоеточие).

Алгоритм работы восходящего распознавателя с возвратами при разборе цепоч­ки а+(а*Ь) будет выполнять следующие шаги:

{q, 1, К Ц

{q, 2, а, [0]}

{q. 2, S, [6,0]}

{q, 3, S+, [0,6,0]}

{q, 4, S+(, [0,0,6,0]}

{q, 5, S+(a, [0,0,0,6,0]}

{q, 5, S+(S, [6,0,0,0,6,0]}

{q, 6, S+(S*, [0,6,0,0,0,6,0]}

{q, 7, S+(S*b, [0,0,6,0,0,0,6,0]}

{q, 7, S+(S*S, [7,0,0,6,0,0,0,6,0]}

На самом деле исходная грамматика для арифметических выражений, которая была рас­смотрена в разделе «Проблемы однозначности и эквивалентности грамматик», тоже не содержит циклов (это легко заметить из вида ее правил), однако для чистоты утвержде­ния цепные правила были исключены. Кроме того, следует отметить, что рассмотренные грамматики эквивалентны (задают один и тот же язык) — это можно утверждать, по­скольку обе они были получены из одной и той же фамматики путем строгих преобразо­ваний, не меняющих заданный грамматикой язык.

11. 2: {q, 8, S+(S*S), [0,7,0,0,6,0,0,0,6,0]}

12. 4: {b, 8, S+(S*S), [0,7,0,0,6,0,0,0,6,0]}

13. 5: {b, 7, S+(S*S, [7,0,0,6,0,0,0,6,0]}

14. 5: {q, 7, S+(S*T, [12,0,0,6,0,0,0,6,0]}

15. 2: {q, 8, S+(S*T), [0,12,0,0,6,0,0,0,6,0]}

16. 4: (b, 8, S+(S*T), [0,12,0,0,6,0,0,0,6,0]}

17. 5: (b, 7, S+(S*T, [12,0,0,6,0,0,0,6,0]}

18. 5: {q, 7, S+(S*E, [15,0,0,6,0,0,0,6,0]}

19. 2: {q, 8, S+(S*E), [0,15,0,0,6,0,0,0,6,0]}

20. 4: {b, 8, S+(S*E), [0,15,0,0,6,0,0,0,6,0]}

21. 5: {b, 7, S+(S*E, [15,0,0,6,0,0,0,6,0]}

22. 5: {q, 8, S+(S*a), [0,0,0,6,0,0,0,6,0]}

23. 4: {b, 8, S+(S*a), [0,0,0,6,0,0,0,6,0]}

24. 5: (b, 7, S+(S*a, [0,0,6,0,0,0,6,0]}

25. 5: {b, 6, S+(S*, [0,6,0,0,0,6,0]}

26. 5: {b, 5, S+(S, [6,0,0,0,6,0]}

27. 5:{q,5,S+(T, [11,0,0,0,6,0]}

28. 2:{q, 6, S+(T*, [0,11,0,0,0,6,0]}

29. 2: {q, 7, S+(T*b, [0,0,11,0,0,0,6,0]}

30. 1: {q, 7, S+(T*S, [7,0,0,11,0,0,0,6,0]}

31. 2: {q, 8, S+(T*S), [0,7,0,0,11,0,0,0,6,0]}

32. 4: {b, 8, S+(T*S), [0,7,0,0,11,0,0,0,6,0]}

33. 5: {b, 7, S+(T*S, [7,0,0,11,0,0,0,6,0]}

34. 5: {q, 7, S+(T*T, [12,0,0,11,0,0,0,6,0]}

35. 2: {q, 8, S+(T*T), [0,12,0,0,11,0,0,0,6,0]}

36. 4: {b, 8, S+(T*T), [0,12,0,0,11,0,0,0,6,0]}

37. 5: {b, 7, S+(T*T, [12,0,0,11,0,0,0,6,0]}

38. 5: {q, 7, S+(T*E, [15,0,0,11,0,0,0,6,0]}

39. 1: (q, 7, S+(S, [3,15,0,0,11,0,0,0,6,0]}

40. 2: {q, 8, S+(S), [0,3,15,0,0,11,0,0,0,6,0]}

41. 1: {q, 8, S+S, [5,0,3,15,0,0,11,0,0,0,6,0]}

42. 4: {b, 8, S+S, [5,0,3,15,0,0,11,0,0,0,6,0]}

43. 5: {q, 8, S+T, [10,0,3,15,0,0,11,0,0,0,6,0]}

44. 1: {q, 8, S, [1,10,0,3,15,0,0,11,0,0,0,6,0]}

3: Разбор закончен, алгоритм завершен.

На основании полученной цепочки номеров правил: 1, 10, 3, 15, 11, 6 получаем правосторонний вывод: S => S+T => S+(S) => S+(T*E) => S+(T*b) => S+(a*b) => a+(a*b). Соответствующее ему дерево вывода приведено на рис. 11.3.

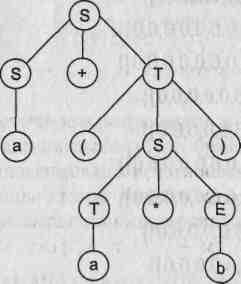
Рис. 11.3. Дерево вывода для грамматики без цепных правил

В приведенном примере очевиден тот же недостаток алгоритма восходящего разбора с возвратами, что и у алгоритма нисходящего разбора с возвратами — значительная временная емкость: для разбора достаточно короткой входной це­почки (всего 7 символов) потребовалось 45 шагов работы алгоритма. Такого результата и следовало ожидать, исходя из экспоненциальной зависимости необ­ходимых для работы алгоритма вычислительных ресурсов от длины входной це­почки. Это существенный недостаток данного алгоритма.

Преимущество у данного алгоритма то же, что и у алгоритма нисходящего раз­бора с возвратами — простота реализации. Поэтому и использовать его можно практически в тех же случаях — когда известно, что длина исходной цепочки символов заведомо не будет большой (не больше нескольких десятков симво­лов).

Этот алгоритм также универсален. На его основе можно распознавать входные цепочки языка, заданного любой КС-грамматикой, достаточно лишь преобразо­вать ее к приведенному виду (а это можно сделать с любой грамматикой, см. раз­дел «Преобразование КС-грамматик. Приведенные грамматики»), чтобы она не содержала цепных правил и ^-правил.

Сам по себе алгоритм «сдвиг-свертка» с возвратами не находит применения в ре­альных компиляторах. Однако его базовые принципы лежат в основе многих восходящих распознавателей, строящих правосторонние выводы и работающих без использования возвратов. Методы, позволяющие строить такие распознава­тели для некоторых классов КС-языков, рассмотрены далее. Эти распознаватели будут более эффективны в смысле потребных вычислительных ресурсов, но ал­горитмы их работы уже сложнее, кроме того, они не являются универсальными. В тех случаях, когда удается дать однозначные ответы на поставленные выше три вопроса о выполнении сдвига (переноса) или свертки при моделировании данного алгоритма, он оказывается очень удобным и полезным.

В принципе два рассмотренных алгоритма — нисходящего и восходящего разбо ра с возвратами — имеют схожие характеристики по потребным вычислитель ным ресурсам и одинаково просты в реализации. То, какой из них лучше взят для реализации простейшего распознавателя в том или ином случае, зависи прежде всего от грамматики языка. В рассмотренном примере восходящий алгс ритм смог построить вывод за меньшее число шагов, чем нисходящий — но эт еще не значит, что он во всех случаях будет эффективнее для рассмотренног языка арифметических выражений. Вопрос о выборе типа распознавателя — нис ходящий либо восходящий — достаточно сложен. В компиляторах на него кром структуры правил грамматики языка влияют и другие факторы, например, нео£ ходимость локализации ошибок в программе, а также то, что предложения все языков программирования строятся в нотации «слева направо». Этот вопро будет затронут далее, при рассмотрении других вариантов распознавателей дл КС-языков; пока же эти два типа распознавателей можно считать сопоставимь ми по эффективности (отметим — низкой эффективности) своей работы и прс стоте реализации.

Табличные распознаватели для КС-языков

Общие принципы работы табличных распознавателей

Табличные распознаватели используют для построения цепочки вывода К( грамматики другие принципы, нежели МП-автоматы. Как и МП-автоматы, ог получают на вход цепочку входных символов а = aia₂...a_n, aeVT*, |a| = n,an строение вывода основывают на правилах заданной КС-грамматики G(VT,VN,P,S Принцип их работы заключается в том, что искомая цепочка вывода строится ) сразу — сначала на основе входной цепочки порождается некоторое промеж точное хранилище информации объема п*п (промежуточная таблица)¹, а поте уже на его основе строится вывод.

Табличные алгоритмы обладают полиномиальными характеристиками требу мых вычислительных ресурсов в зависимости от длины входной цепочки. Д. произвольной КС-грамматики G(VT,VN,P,S) время выполнения алгоритма ' имеет кубическую зависимость от длины входной цепочки, а необходимый об ем памяти М_э — квадратичную зависимость от длины входной цепочки: а, ае V п = |а|: Т_э = 0(п³) и М_э = 0(п²), Квадратичная зависимость объема необходим! памяти от длины входной цепочки напрямую связана с использованием пром жуточного хранилища данных.

¹ В алгоритме Кока—Янгера—Касами промежуточная таблица используется в явном ви, а в алгоритме Эрли она завуалирована под хранилище, именуемое «список ситуацш которое организовано несколько сложнее, чем простая таблица.

Табличные распознаватели универсальны — они могут быть использованы для распознавания цепочек, порожденных с помощью произвольной КС-грамматики (возможно, саму грамматику первоначально потребуется привести к заданному виду, но это не ограничивает универсальности алгоритмов). Кроме того, таблич­ные распознаватели — это самые эффективные с точки зрения требуемых вычис­лительных ресурсов универсальные алгоритмы для распознавания цепочек КС-языков¹,

Алгоритм Кока—Янгера—Касами

Алгоритм Кока—Янгера—Касами для заданной грамматики G(VT,VN,P,S) и цепочки входных символов а = aia₂...a_n, aeVT*, |a| = п строит таблицу Т_п._п, та­кую, что VAeVN: AeT[i,j], тогда и только тогда, если A=>+a_i...a_i+j.₁. Таким обра­зом, элементами таблицы Т_п»_п являются множества нетерминальных символов из алфавита VN.

Тогда существованию вывода S=>*a соответствует условие SeT[l,n].

При условии существования вывода по таблице Т_п._п можно найти всю полную цепочку вывода S=s>*a.

Для построения вывода по алгоритму Кока—Янгера—Касами грамматика G(VT, VN,P,S) должна быть в нормальной форме Хомского. Поскольку, как было пока­зано выше, любую произвольную КС-грамматику можно преобразовать в нор­мальную форму Хомского, это не накладывает дополнительных ограничений на применимость данного алгоритма.

Алгоритм Кока—Янгера—Касами фактически состоит из трех вложенных цик­лов. Поэтому ясно, что время выполнения алгоритма имеет кубическую зависи­мость от длины входной цепочки символов. Таблица Т_п»_п, используемая для хра­нения промежуточных данных в процессе работы алгоритма, является таблицей множеств. Очевидно, что требуемый для ее хранения объем памяти имеет квад­ратичную зависимость от длины входной цепочки символов.

Сам алгоритм Кока—Янгера—Касами можно описать следующим образом:

Шаг 1.

Цикл для j от 1 до п

T[l.j] := {А | 3 АтМ, eP}-i T[l,j] включаются все нетерминальные символы,

для которых в грамматике G существует правило А->а.,.

Конец цикла для j.

Хотя табличные распознаватели и являются самыми эффективными среди универсаль­ных распознавателей, тем не менее они не находят широкого применения. Дело в том, что полиномиальная зависимость требуемых вычислительных ресурсов от длины входной цепочки символов является неудовлетворительной для компиляторов (длины входных цепочек — тысячи и десятки тысяч символов). Поэтому практически всегда используют­ся не универсальные, а более узкие, специализированные алгоритмы распознавателей, которые имеют обычно линейную зависимость требуемых вычислительных ресурсов от длины входной цепочки символов. К универсальным алгоритмам прибегают только то­гда, когда специализированный распознаватель построить не удается. Шаг 2.

Цикл для i от 2 до п

Цикл для j от 1 до n-1+l T[i.j] := 0; Цикл для к от 1 до п-1

Tti.j] : = T[i.j] и {А | .3 А^ВС € P. BeT[k.j]. CeT[i-k.j+k]} Конец цикла для к. Конец цикла для j. Конец цикла для i. Результатом работы алгоритма будет искомая таблица Т_п._п. Для проверки супц ствования вывода исходной цепочки в заданной грамматике остается только прс верить условие SeT[l,n].

Если вывод существует, то необходимо получить цепочку вывода. Для этот, существует специальная рекурсивная процедура R. Она выдает последовательность номеров правил, которые нужно применить, чтобы получить цепочку вь вода. Ее можно описать следующим образом: R(i,j,A), где AeVN.

1. Если j = 1 и существует правило A-»aj, то выдать номер этого правила.

2. Иначе (если j > 1) возьмем к как наименьшее из чисел, для которых 3 А--»ВХ е Р, BeT[k,j], CeT[i-k,j+k] (таких правил может быть несколько, д; определенности берем наименьшее к). Пусть правило А-»ВС имеет номер i Тогда нужно выдать этот номер ш, потом вызвать сначала R(i,k,B), а затем R(i-k,j+k,C).

Для получения всей последовательности номеров правил нужно вызвать R(l,n,S Рекурсивная процедура R не требует дополнительной памяти для своего выпо нения, кроме стека, необходимого для организации рекурсии. Время ее выполн ния имеет квадратичную зависимость от длины входной цепочки. На основании последовательности номеров правил, полученной с помощью алг ритма Кока—Янгера—Касами и рекурсивной процедуры R, можно построить лев сторонний вывод для заданной грамматики G(VT,VN,P,S) и цепочки входных си волов а. Таким образом, с помощью данного алгоритма решается задача разбора.

Алгоритм Эрли (основные принципы)

Алгоритм Эрли основан на том, что для заданной КС-грамматики G(VT,VN,P, и входной цепочки со = а^.-.а,,, goeVT, |со| = п строится последовательность era ков ситуаций 1₀,1_1?..., 1_п. Каждая ситуация, входящая в список Ij для входной i почки со, представляет собой структуру вида [A->X₁X₂...X_k»X_k+1...X_m,i], N X_ke(VNuVT), причем правило A-^Х^..Х,,, принадлежит множеству правил грамматики G, и 0<i<n, 0<k<m. Символ • («точка») — это метасимвол особе вида, который не входит ни во множество терминальных (VN), ни во множе! во нетерминальных (VT) символов грамматики. В ситуации этот символ мои стоять в любой позиции, в том числе в начале (•Щ.:.Х_т) или в конце (Х)...Х, всей цепочки символов правила А->Х)...Х_т. Если цепочка символов правг пустая (А—>Х), то ситуация будет выглядеть так: [A—>«,i]. Список ситуаций строится таким образом, что Vj, 0<j<n: [A->a»p,i]eIj тогда и только тогда, если 3 S=>*yAS, у=>*а1...а, и a=>*a_i+1...aj. Иначе говоря, между вто­рым компонентом ситуации и номером списка, в котором он появляется, заклю­чена часть входной цепочки, выводимая из А. Условия ситуации L гарантируют возможность применения правила А-»сф в выводе некоторой входной цепочки, совпадающей с заданной цепочкой со до позиции j.

Условием существования вывода заданной входной цепочки со в грамматике G(VN,VT,P,S) после завершения алгоритма Эрли служит [S-Ko»,0]sl_n. На осно­вании полученного в результате выполнения алгоритма списка ситуаций можно затем с помощью специальной процедуры построить всю цепочку вывода и по­лучить номера применяемых правил. Причем проще построить правосторонний вывод.

Алгоритм Эрли подробно здесь не рассматривается. Его описание можно найти, например, в книге [6, т. 1].

Как и все табличные алгоритмы, алгоритм Эрли обладает полиномиальными характеристиками в зависимости от длины входной цепочки. Доказано, что для произвольной КС-грамматики G(VN,VT,P,S) время выполнения данного алго­ритма Т_э будет иметь кубическую зависимость от длины входной цепочки, а не­обходимый объем памяти М_э — квадратичную зависимость от длины входной цепочки: а, ае VT*, п т |а|: Т_э = 0(п³) и М_э = 0(п²). Но для однозначных КС-грамматик алгоритм Эрли имеет лучшие характеристики — его время выполне­ния в этом случае квадратично зависит от длины входной цепочки: Т_э = 0(п²). Кроме того, для некоторых классов КС-грамматик время выполнения этого ал­горитма линейно зависит от длины входной цепочки (правда, для этих классов, как правило, существуют более простые алгоритмы распознавания). В целом алгоритм Эрли имеет лучшие характеристики среди всех универсаль­ных алгоритмов распознавания входных цепочек для произвольных КС-грамма­тик. Он превосходит алгоритм Кока—Янгера—Касами для однозначных грамма­тик (которые представляют интерес в первую очередь), хотя и является более сложным в реализации.

Принципы построения распознавателей КС-языков без возвратов

Выше были рассмотрены различные универсальные распознаватели для КС-языков — то есть распознаватели, позволяющие выполнить разбор цепочек для любого КС-языка (заданного произвольной КС-грамматикой). Они универсаль­ны, но имеют неудовлетворительные характеристики. Распознаватели с возвра­тами имеют экспоненциальную зависимость требуемых для выполнения алго­ритма разбора вычислительных ресурсов от длины входной цепочки символов, а табличные распознаватели — полиномиальную. Для практического примене­ния в реальных компиляторах такие характеристики являются неудовлетвори­тельными. К сожалению, универсальных распознавателей с лучшими характеристиками для КС-языков построить не удается. Среди универсальных распознавателей лучши­ми по эффективности являются табличные.

С другой стороны, универсальные распознаватели для КС-языков на практике и не требуются. В каждом конкретном случае компилятор имеет дело с синтак­сическими структурами, заданными вполне определенной грамматикой. Чаще всего эта грамматика является не просто КС-грамматикой, а еще и относится к какому-нибудь из известных классов КС-грамматик (нередко сразу к несколь­ким классам). Как минимум грамматика синтаксических конструкций языка про­граммирования должна быть однозначной, а это уже значит, что она относится к классу детерминированных КС-языков.

Для многих классов КС-грамматик (и соответствующих им классов КС-языков) можно построить распознаватели, имеющие лучшие характеристики, чем рассмот­ренные выше распознаватели с возвратами и табличные. Эти распознаватели уже не будут универсальными — они будут применимы только к заданному классу КС-языков с соответствующими ограничениями, зато они будут иметь лучшие характеристики.

Далее будут рассмотрены некоторые из таких распознавателей. Все они имеют линейные характеристики — линейную зависимость необходимых для выпол­нения алгоритма разбора вычислительных ресурсов от длины входной цепочки. Для каждого распознавателя рассматривается класс КС-грамматик, с которым он связан. Это значит, что он может принимать только входные цепочки из КС-языков, заданных такими грамматиками. Всегда описываются ограничения, на­лагаемые на правила грамматики, или дается алгоритм проверки принадлежно­сти произвольной КС-грамматики к заданному классу.

Однако следует всегда помнить, что проблема преобразования КС-грамматик алго­ритмически неразрешима. Если какая-то грамматика не принадлежит к требуе­мому классу КС-грамматик, это еще не значит, что заданный ею язык не может быть описан грамматикой такого класса. Иногда удается выполнить преобразо­вания и привести исходную грамматику к требуемому виду. Но, к сожалению, этот процесс не формализован, не поддается алгоритмизации и требует участия человека. Чаще всего такую работу вынужден выполнять разработчик компиля­тора (правда, выполняется она только один раз для синтаксических конструкций каждого языка программирования).

Существуют два принципиально разных класса распознавателей. Первый — нис­ходящие распознаватели, которые порождают цепочки левостороннего вывода и строят дерево вывода сверху вниз. Второй — восходящие распознаватели, кото­рые порождают цепочки правостороннего вывода и строят дерево вывода снизу вверх. Названия «нисходящие» и «восходящие» связаны с порядком построения дерева вывода. Как правило, все распознаватели читают входную цепочку симво­лов слева направо, поскольку предполагается именно такая нотация в написании исходного текста программ.

Нисходящие распознаватели используют модификации алгоритма с подбором альтернатив. При их создании применяются методы, которые позволяют одно­значно выбрать одну и только одну альтернативу на каждом шаге работы МП-

автомата (шаг «выброс» в этом автомате всегда выполняется однозначно). Алго­ритм подбора альтернатив без модификаций был рассмотрен выше.

Восходящие распознаватели используют модификации алгоритма «сдвиг-сверт­ка» (или «перенос-свертка», что то же самое). При их создании применяются методы, которые позволяют однозначно выбрать между выполнением «сдвига» («переноса») или «свертки» на каждом шаге работы расширенного МП-автома­та, а при выполнении свертки однозначно выбрать правило, по которому будет производиться свертка. Алгоритм «сдвиг-свертка» без модификаций был рассмот­рен выше.

Далеко не все известные распознаватели с линейными характеристиками рассмат­риваются в данном пособии. Более полный набор распознавателей, а также опи­сание связанных с ними классов КС-грамматик и КС-языков вы можете найти в [5, 6, 23, 42, 65]. Далее будут рассмотрены только самые часто встречающиеся и употребительные классы.

Классы кс-языков и грамматик.

Нисходящие распознаватели КС-языков без возвратов

Левосторонний разбор по методу рекурсивного спуска

Стремление улучшить алгоритм нисходящего разбора заключается в первую очередь в определении метода, по которому на каждом шаге алгоритма можно был бы однозначно выбрать одну из всего множества возможных альтернатив. В тг ком случае алгоритм моделирования работы МП-автомата не требовал бы возврг та на предыдущие шаги и за счет этого обладал бы линейными характеристике ми от длины входной цепочки. В случае неуспеха выполнения такого алгоритм входная цепочка однозначно не принимается, повторные итерации разбора н выполняются.

Наиболее очевидным методом выбора одной из множества альтернатив являете выбор ее на основании символа ае VT, обозреваемого считывающей головкой ai томата на каждом шаге его работы (находящегося справа от положения текуще головки во входной цепочке символов). Поскольку в процессе нисходящего ра: бора именно этот символ должен появиться на верхушке магазина для продв! жения считывающей головки автомата на один шаг (условие 5(q,a,a) = {(q,^-) VaeVT в функции переходов МП-автомата), то разумно искать альтернатив где он присутствует в начале цепочки, стоящей в правой части правила грамм; тики. По такому принципу действует алгоритм разбора по методу рекурсивного спуска

Алгоритм разбора по методу рекурсивного спуска

В реализации этого алгоритма для каждого нетерминального символа AeV грамматики G(VN,VT,P,S) строится процедура разбора, которая получает i вход цепочку символов а и положение считывающей головки в цепочке i. Ecj для символа А в грамматике G определено более одного правила, то процедура разбора ищет среди них правило вида А-»ау, aeVT, ye(VNuVT)*, первый сим­вол правой части которого совпадал бы с текущим символом входной цепочки а = оц. Если такого правила не найдено, то цепочка не принимается. Иначе (если найдено правило А-»ау или для символа А в грамматике G существует только одно правило А-»у), то запоминается номер правила, и когда а = ocj, то считываю­щая головка передвигается (увеличивается i), а для каждого нетерминального символа в цепочке у рекурсивно вызывается процедура разбора этого символа. Название метода происходит из реализации алгоритма, которая заключается в последовательности рекурсивных вызовов процедур разбора. Для начала разбо­ра входной цепочки нужно вызвать процедуру для символа S с параметром i = 1.

Условия применимости метода можно получить из описания самого алгорит­ма—в грамматике G(VN,VT,P,S) VAeVN возможны только два варианта пра­вил:

А->у, ye(VNuVT)* и это единственное правило для А;

A->a,pi|a₂p₂|...|a_np_n, Vi: a_ieVT, p_i6(VNuVT)* и если щ, то аЦ.

Этим условиям удовлетворяет незначительное количество реальных грамматик. Это достаточные, но не необходимые условия. Если грамматика не удовлетворя­ет этим условиям, еще не значит, что заданный ею язык не может распознаваться с помощью метода рекурсивного спуска. Возможно, над грамматикой просто не­обходимо выполнить ряд дополнительных преобразований.

К сожалению, не существует алгоритма, который бы позволил преобразовать произвольную КС-грамматику к указанному выше виду, равно как не существу­ет и алгоритма, который бы позволял проверить, возможны ли такого рода пре­образования. То есть для произвольной КС-грамматики нельзя сказать, анализи­руема ли она методом рекурсивного спуска или нет.

Можно рекомендовать ряд преобразований, которые способствуют приведению грамматики к требуемому виду, но не гарантируют его достижения.

1. Исключение ^-правил.

2. Исключение левой рекурсии.

3. Добавление новых нетерминальных символов. Например:

если правило: A->aa₁|aa₂|...|aa_n|b₁p₁|b₂p₂|...|b_mp_m,

то заменяем его на два: А-»аА'| b₁p₁|b₂p₂l—|b_mp_m и A'—>cc₁jot₂|---|a._n.

4. Замена нетерминальных символов в правилах на цепочки их выводов. Например:

если имеются правила:

A->B₁|B₂|...|B_n|b₁p,|b₂p₂|...|b_mp_mi

Bj-KXnIa^Ulcq,,,

B_n->a_nl|a_n2|...|a

заменяем первое правило на A^a_n|a₁₂|...|a_lk|...|a_nl|a_n2|...|a_np|b₁p₁|b₂p₂|...|b_mp_m.

В целом алгоритм рекурсивного спуска эффективен и прост в реализации, но имеет очень ограниченную применимость.

Пример реализации метода рекурсивного спуска

Дана грамматика G({a,b,c},{A,B,C,S},P,S):

Р:

S -> аА | ЬВ

А -> а | ЬА | сС

В -> b | аВ | сС

С.-> АаВЬ Необходимо построить распознаватель, работающий по методу рекурсивного спуска.

Видно, что грамматика удовлетворяет условиям, необходимым для построения такого распознавателя.

Напишем процедуры на языке программирования С, которые будут обеспечи­вать разбор входных цепочек языка, заданного данной грамматикой. Согласно алгоритму, необходимо построить процедуру разбора для каждого нетерминаль­ного символа грамматики, поэтому дадим процедурам соответствующие наиме­нования. Входные данные для процедур разбора будут следующие:

• цепочка входных символов;

• положение указателя (считывающей головки МП-автомата) во входной це­почке;

• массив для записи номеров примененных правил;

• порядковый номер очередного правила в массиве.

Результатом работы каждой процедуры может быть число, отличное от нуля («истина»), или 0 («ложь»). В первом случае входная цепочка символов прини­мается распознавателем, во втором случае — не принимается. Для удобства реа­лизации в том случае, если цепочка принимается распознавателем, будем воз­вращать текущее положение указателя в цепочке. Кроме того, потребуется еще одна дополнительная процедура для ведения записей в массиве последователь­ности правил (назовем ее WriteRules).

void WriteRulesdnt* piRul. int* iP, int iRule)

{

piRul[*iP] = iRule;

*iP - *iP + 1; }

int proc_S (char* szS, int IN, int* piRul, int* iP)

{

switch CszSCiN])

case а :

WriteRules(piRul.iP.l);

return proc_A(szS.iN+l.piRul .iP); case 'b':

WriteRules(piRul.iP,2):

return proc_B(szS.iN+l,piRul,iP);

return 0:

int proc_A (char* szS. int iN. int* piRul. int* iP) {

switch CszS[iN])

{

case 'a':

writeRu1es(piRul,iP.3);

return iN+1: case 'b':

WriteRules(piRul,iP.4):

return proc_A(szS.1N+l,piRul,i P); case 'c':

WnteRules(piRul.iP,5);

return proc_C(szS.iN+l.piRul,iP);

} return 0;

}

int proc_B (char* szS. int iN. int* piRul. int* iP) {

switch (szS[iN])

{

case 'b':

WriteRules(piRul,iP,6): return iN+1; case 'a':

WriteRules(piRul.iP.7); return proc_B(szS,iN+l,piRul.iP); case 'c':

WriteRules(piRul.iP,8); return proc_B(szS.i N+l,pi Rul.i P); } return 0;

}

int proc_C (char* szS, int iN, int* piRul. int* iP) { i nt i;

WriteRules(piRu1.iP,9): i = proc_A(szS.iN,piRul .iP); if (i «— 0) return 0; if (szS[i] != 'a') return 0; i++;

i - proc_B(szS,i.piRul.iP); if (i == 0) return 0; if (szS[i] != 'b') return 0: return i+1: }

Теперь для распознавания входной цепочки необходимо иметь целочисленный массив Rules достаточного объема для хранения номеров правил. Тогда работа распознавателя заключается в вызове процедуры proc_S(Str,0,Rules,&N), где Str -это входная цепочка символов, N — переменная для запоминания количества при­мененных правил (первоначально N = 0). Затем требуется обработка полученно­го результата: если результат на 1 превышает длину цепочки — цепочка принята, иначе — цепочка не принята. В первом случае в массиве Rules будем иметь по­следовательность номеров правил грамматики, необходимых для вывода цепоч­ки, а в переменной N — количество этих правил. На основе этой цепочки можнс легко построить дерево вывода.

Объем массива Rul es заранее не известен, так как заранее не известно количестве шагов вывода. Чтобы избежать проблем с недостаточным объемом статическогс массива, приведенные выше процедуры распознавателя можно модифицировал так, чтобы они работали с динамическим распределением памяти (изменив про­цедуру WriteRules и тип параметра pi Rul в вызовах остальных процедур). На ло­гику работы распознавателя это никак не повлияет. Следует помнить также, чте метод рекурсивного спуска основан на рекурсивном вызове множества проце­дур, что при значительной длине входной цепочки символов может потребовал соответствующего объема стека вызовов для хранения адресов процедур, их па­раметров и локальных переменных (более подробно об этом можно посмотрел в данном пособии в разделе «Семантический анализ и подготовка к генерации кода», глава 14).

Из приведенного примера видно, что алгоритм рекурсивного спуска удобен и прост в реализации. Главным препятствием в его применении является то, что класс грамматик, допускающих разбор на основе этого алгоритма, сильно ограничен.

Расширенное применение распознавателей на основе метода рекурсивного спуска

Метод рекурсивного спуска позволяет выбрать альтернативу, ориентируясь нг текущий символ входной цепочки, обозреваемый считывающей головкой МП автомата. Если имеется возможность просматривать не один, а несколько симво лов вперед от текущего положения считывающей головки, то можно расширит! область применимости метода рекурсивного спуска. В этом случае уже можнс искать правила на основе некоторого терминального символа, входящего в пра вую часть правила. Естественно, и в таком варианте выбор должен быть однознач

ным — для каждого нетерминального символа в левой части правила необходи­мо, чтобы в правой части правила не встречалось двух одинаковых терминальных символов.

Этот метод требует также анализа типа присутствующей в правилах рекурсии, поскольку один и тот же терминальный символ может встречаться во входной строке несколько раз, и в зависимости от типа рекурсии следует искать его край­нее левое или крайнее правое вхождение в строке.

Рассмотрим грамматику арифметических выражений без скобок для символов aHbG({+, -./.*. a, b}. {S.T.E}, Р, S):

Р:

S -> S+T | S-T | Т

Т -> Т*Е | Т/Е | Е

Е -» (S) | a | b Это грамматика для арифметических выражений, которая уже была рассмотрена в разделе «Проблемы однозначности и эквивалентности грамматик», глава 9 и служила основой для построения распознавателей в разделе «Распознаватели КС-языков с возвратом», глава 11.

Запишем правила этой грамматики в форме с применением метасимволов. По­лучим:

Р:

S ^ Т{(+Т,-Т)}

Т -» Е{(*Е,/Е)}

Е -> (S) | а | b При такой форме записи процедура разбора для каждого нетерминального сим­вола становится тривиальной.

Для символа S распознаваемая строка должна всегда начинаться со строки, до­пустимой для символа Т, за которой может следовать любое количество симво­лов + или -, и если они найдены, то за ними опять должна быть строка, допусти­мая для символа Т. Аналогично, для символа Т распознаваемая строка должна всегда начинаться со строки, допустимой для символа Е, за которой может сле­довать любое количество символов * или /, и если они найдены, то за ними опять должна быть строка, допустимая для символа Е. С другой стороны, для симво­ла Е строка должна начинаться строго с символов (, а или Ь, причем в первом случае за ( должна следовать строка, допустимая для символа S, а за ней — обя­зательно символ ).

Исходя из этого, построены процедуры разбора входной строки на языке Pascal (используется Borland Pascal или Borland Delphi, которые допускают тип string — строка). Входными данными для них являются:

• исходная строка символов;

• текущее положение указателя в исходной строке;

• длина исходной строки (в принципе, этот параметр можно опустить, но он введен для удобства);

• результирующая строка правил.

Процедуры построены так, что в результирующую строку правил помещаются номера примененных правил в строковом формате, перечисленные через запя­тую (.). Правила номеруются в грамматике, записанной в форме Бэкуса—Наура, в порядке слева направо и сверху вниз (всего в исходной грамматике 9 правил). Распознаватель строит левосторонний вывод, поэтому на основе строки номеров правил всегда можно получить цепочку вывода или дерево вывода. Для начала разбора нужно вызвать процедуру proc_S(S,l,N,Pr), где S — входная строка символов; N — длина входной строки (в языке Borland Pascal вместо N можно взять Length(S)); Pr — строка, куда будет помещена последовательность примененных правил.

Результатом proc_S(S,l,N,Pr) выполнения будет N+1, если строка S принимается, и некоторое число, меньшее N+1, если строка не принимается. Если строка S при­нимается, то строка Рг будет содержать последовательность номеров правил, ко­торые необходимо применить для того, чтобы вывести S¹.

procedure proc_S (S; string: i.n: integer; var pr: string): integer:

var si : string:

begin

i :* proc_T(S.i,n,sl); if 1 > 0 then begin

pr := '3.' + si: while (i <* n) and (i <> 0) do case S[i] of '+'_: begin

if i = n then i :» 0

else

begin

i := proc_T(S.i+l,n,sl): pr := '1.' + pr +'.'+ si; end: end: '-': begin

if i = n then i := 0

else

begin

i := proc_T(S,i+l.n,sl): pr := '2,' + pr +'.'+ si:

¹ Использование языка программирования Borland Pascal накладывает определенные тех­нические ограничения на данный распознаватель - длина строки в этом языке не может превышать 255 символов. Однако данные ограничения можно снять если реализовать свои тип данных «строка», или используя тот же алгоритм в другом языке программиоо-вания. При использовании Borland Delphi эти ограничения отпадают Конечно такого рода ограничения не имеют принципиального значения при теоретическом исслеловя нии работы распознавателя, тем не менее автор считает необходимым упомянуть о них

end:
end:
else break;
end;{case}
end;{if}
proc_S :- i:
end;
procedure proc_S (S; string;	i,n: integer; var pr:		string): integer
var si : string;
begin
i := proc_E(S.i.n.sl):
if i > 0 then
begin
pr ;= '6.' + si;
while (i <= n) and (i	<> 0) do
case S[i] of
.'*': begin
if i - n then	i :- 0
else
begin
i := proc_	E(S.i+l.n	si);
pr : = '4,'	+ pr +',	+ si:
end;
end;
7'; begin
if i = n then	i := 0
else
begin
i := proc	_E(S.i+l.r	.si);
pr ;= '5.	' + pr +'	' + si:
end;
end;
else break;
end;{case}
end;{if}
proc_S ;= i;
end;

procedure procJ (S: string: i.n: integer; var pr: string): integer:

var si : string:

begin

case S[i] of 'a': begin pr := '8': proc_E := i+1: end;

'to': begin рг := '9'; ргос_Е := i+1; end:

'С: begin '

ргос_Е :- 0; if i < n then begin

i := proc_S(S.i+l.n.sl); if (i > 0) and (i < n) then begin

pr := '7,' + si;

if S[i] = ')' then proc_E := i+1; end; end; end;

else proc_E :- 0; end;{case} end;

Конечно, и в данном случае алгоритм рекурсивного спуска позволил построить достаточно простой распознаватель, однако, прежде чем удалось его применить, потребовался неформальный анализ правил грамматики. Далеко не всегда тако­го рода неформальный анализ является возможным, особенно если грамматика содержит десятки и даже сотни различных правил — человек не всегда в состоя­нии уловить их смысл и взаимосвязь. Поэтому расширения алгоритма рекурсив­ного спуска, хотя просты и удобны, но не всегда применимы. Даже понять сам факт того, можно или нет в заданной грамматике построить такого рода распо­знаватель, бывает очень непросто [15, 26, 74].

Далее будут рассмотрены распознаватели и алгоритмы, которые основаны на строго формальном подходе. Они предваряют построение распознавателя рядом обоснованных действий и преобразований, с помощью которых подготавлива­ются необходимые исходные данные. Все такого рода действия построены на ос­нове операций над множествами и символами, а исходными данными для них служат множества символов и правил исходной грамматики. В этом случае под­готовку всех исходных данных для распознавателя можно формализовать и ав­томатизировать вне зависимости от объема грамматики (количества правил и символов в ней). Эти предварительные действия можно выполнить на компью­тере, в то время как расширенная трактовка рекурсивного спуска предполагает неформальный анализ грамматики человеком, и в этом серьезный недостаток метода.

Определение 1_Цк)-грамматики

Логическим продолжением идеи, положенной в основу метода рекурсивного спус­ка, является предложение использовать для выбора одной из множества альтер­натив не один, а несколько символов входной цепочки. Однако напрямую пере- дожить алгоритм выбора альтернативы для одного символа на такой же алгоритм для цепочки символов не удастся — два соседних символа в цепочке на самом деле могут быть выведены с использованием различных правил грамматики, по­этому неверным будет напрямую искать их в одном правиле. Тем не менее суще­ствует класс грамматик, основанный именно на этом принципе — выборе одной альтернативы из множества возможных на основе нескольких очередных симво­лов в цепочке. Это так называемые LL(k)-грамматики. Правда, алгоритм работы распознавателя для них не так очевидно прост, как рассмотренный выше алго­ритм рекурсивного спуска.

Грамматика обладает свойством LL(k), k > 0, если на каждом шаге вывода для однозначного выбора очередной альтернативы МП-автомату достаточно знать символ на верхушке стека и рассмотреть первые к символов от текущего поло­жения считывающей головки во входной цепочке символов. Грамматика называется LL(k)-грамматикой, если она обладает свойством LL(k) для некоторого к > О¹.

Название «LL(k)>> несет определенный смысл. Первая литера «L» происходит от слова «left» и означает, что входная цепочка символов читается в направлении слева направо. Вторая литера «L» также происходит от слова «left» и означает, что при работе распознавателя используется левосторонний вывод. Вместо «к» в названии класса грамматики стоит некоторое число, которое показывает, сколь­ко символов надо рассмотреть, чтобы однозначно выбрать одну из множества аль­тернатив. Так, существуют LL(1)-грамматики, 1Х(2)-грамматики и другие классы.

В совокупности все П_(к)-грамматики для всех к>0 образуют класс LL-грам-матик.

На рис. 12.1 схематично показано частичное дерево вывода для некоторой LL(k)-грамматики. В нем ю обозначает уже разобранную часть входной цепочки а, ко­торая построена на основе левой части дерева у. Правая часть дерева х — это еще не разобранная часть, а А — текущий нетерминальный символ на верхушке стека МП-автомата. Цепочка х представляет собой незавершенную часть цепочки вы­вода, содержащую как терминальные, так и нетерминальные символы. После за­вершения вывода символ А раскрывается в часть входной цепочки о, а правая часть дерева х преобразуется в часть входной цепочки т. Свойство LL(k) предпо­лагает, что однозначный выбор альтернативы для символа А может быть сделан на основе к первых символов цепочки от, являющейся частью входной цепоч­ки а.

Алгоритм разбора входных цепочек для 1Х(к)-грамматики носит название «к-предсказывающего алгоритма». Принципы его выполнения во многом соответст­вуют функционированию МП-автомата с той разницей, что на каждом шаге ра-

Требование к > 0, безусловно, является разумным — для принятия решения о выборе той или иной альтернативы МП-автомату надо рассмотреть хотя бы один символ входной цепочки. Если представить себе LL-грамматику с к = 0, то в такой грамматике вывод со­всем не будет зависеть от входной цепочки. В принципе такая грамматика возможна, но в ней будет всего одна-единственная цепочка вывода. Поэтому практическое применение языка, заданного такого рода грамматикой, представляется весьма сомнительным. боты этот алгоритм может просматривать к символов вперед от текущего поло­жения считывающей головки автомата.

V	ш	л
1	и - \\	\
со	и	1х
	к
а

Рис. 12.1. Схема построения дерева вывода для Щк)-грамматики

Для LL(k)-грамматик известны следующие полезные свойства:

• всякая 1_Цк)-грамматика для любого к>0 является однозначной;

• существует алгоритм, позволяющий проверить, является ли заданная грамма­тика ЬЦк)-грамматикой для строго определенного числа к.

Кроме того, известно, что все грамматики, допускающие разбор по методу рекур­сивного спуска, являются подклассом ЬЦ1)-грамматик. То есть любая грамма­тика, допускающая разбор по методу рекурсивного спуска, является LL( 1 ^грам­матикой (но не наоборот!).

Есть, однако, неразрешимые проблемы для произвольных КС-грамматик:

• не существует алгоритма, который бы мог проверить, является ли заданная КС-грамматика 1Х(к)-грамматикой для некоторого произвольного числа к;

• не существует алгоритма, который бы мог преобразовать произвольную КС-грамматику к виду ЬЦк)-грамматики для некоторого к (или доказать, что преобразование невозможно).

Это несколько ограничивает применимость ГЦк)-грамматик, поскольку не все­гда для произвольной КС-грамматики можно очевидно найти число к, для кото­рого она является LL(k)-грамматикой, или узнать, существует ли вообще для нее такое число к.

Для ЬЦк)-грамматики при к>1 совсем не обязательно, чтобы все правые части правил грамматики для каждого нетерминального символа начинались с к различ­ных терминальных символов. Принципы распознавания предложений входного языка такой грамматики накладывают менее жесткие ограничения на правила грамматики, поскольку к соседних символов, по которым однозначно выбирает­ся очередная альтернатива, могут встречаться и в нескольких правилах грамма­тики (эти условия рассмотрены ниже). Грамматики, у которых все правые части правил для всех нетерминальных символов начинаются с к различных терми­нальных символов, носят название «сильно ЬЦк)-грамматик». Метод построе­ния распознавателей для них достаточно прост, алгоритм разбора очевиден, но, к сожалению, такие грамматики встречаются крайне редко.

Для LL(l)-rpaMMaTHKH, очевидно, для каждого нетерминального символа не мо­жет быть двух правил, начинающихся с одного и того же терминального симво­ла. Однако это менее жесткое условие, чем то, которое накладывает распознава­тель по методу рекурсивного спуска, поскольку в принципе LL(l)-rpaMMaTHKa допускает в правой части правил цепочки, начинающиеся с нетерминальных символов, а также ^.-правила. LL(l)-rpaMMaTHKH позволяют построить достаточ­но простой и эффективный распознаватель, поэтому они рассматриваются далее отдельно в соответствующем разделе.

Поскольку все LL(k)-rpaMMaTHKH используют левосторонний нисходящий рас­познаватель, основанный на алгоритме с подбором альтернатив, очевидно, что они не могут допускать левую рекурсию. Поэтому никакая леворекурсивная грам­матика не может быть LL-грамматикой. Следовательно, первым делом при по­пытке преобразовать грамматику к виду LL-грамматики необходимо устранить в ней левую рекурсию (соответствующий алгоритм был рассмотрен выше). Класс LL-грамматик широк, но все же он недостаточен для того, чтобы покрыть все возможные синтаксические конструкции в языках программирования (к ним относим все детерминированные КС-языки). Известно, что существуют детер­минированные КС-языки, которые не могут быть заданы LL(k)-грамматикой ни для каких к. Однако LL-грамматики удобны для использования, поскольку по­зволяют построить распознаватели с линейными характеристиками (линейной зависимостью требуемых для работы алгоритма распознавания вычислительных ресурсов от длины входной цепочки символов).

Принципы построения распознавателей для LL(k)-грамматик

Для построения распознавателей LL(k)-rpaMMaraK используются два важных мно­жества, определяемые следующим образом:

• FIRST(k,a) — множество терминальных цепочек, выводимых из ae(VTuVN)*, укороченных до к символов;

• FOLLOW(k.A) — множество укороченных до к символов терминальных це­почек, которые могут следовать непосредственно за AeVN в цепочках вывода.

Формально эти два множества могут быть определены следующим образом: FIRST(k,a) = {coeVT* | либо |со|<к и а=>*со, либо |ео|>к и а=>*сох, xe(VTuVN)*}, ae(VTuVN)*, k>0. FOLLOW(k,A) = {coeVT* | S=>*aAy и coeFIRST(y,k), aeVT*}, AeVN, k>0.

Очевидно, что если имеется цепочка терминальных символов aeVT*, то FIRST(k,a) — это первые к символов цепочки а.

Доказано, что грамматика G(VT,VN,P,S) является LL(k )-грамматикой тогда и только тогда, когда выполняется следующее условие: V А—»р е Р и V А-> ->g е P (pVy): FIRST(k,(3co) n FIRST(k,yco) = 0 для всех цепочек со таких, что S =>* схАсо.

Иначе говоря, если существуют две цепочки вывода: S =>* aAy => azy =>* асо S =>* aAy => aty =>* аи

то из условия FIRST(k,co) = FIRST(k,u) следует, что z = t.

На основе этих двух множеств строится алгоритм работы распознавателя для LL(k)-rpaMMaTHK, который представляет собой k-предсказывающий алгоритм для МП-автомата, заданного так: R({q},VT,Z,5,q,S,{q}), где Z = VTuVN, a S — целевой символ грамматики G. Функция переходов автомата строится на основе управ­ляющей таблицы М, которая отображает множество (Zu{^}) x VT*^k на множест­во, состоящее из следующих элементов:

• пар вида (РД), где (3 — цепочка символов, помещаемая автоматом на верхушку стека, a i — номер правила вида А-»р, AeVN, peZ*;

• «выброс»;

• «допуск»;

• «ошибка».

Конфигурацию распознавателя можно отобразить в виде конфигурации МП-автомата с дополнением цепочки п, в которую помещаются номера применен­ных правил. Поскольку автомат имеет только одно состояние, его в конфигура­ции можно не указывать. Если считать, что X — это символ на верхушке стека автомата, а — непрочитанная автоматом часть входной цепочки символов, а и = FIRST(k,a), то работу алгоритма распознавателя можно представить сле­дующим образом:

• (а, Ху, п) н- (а, Ру, rci), yeZ*, если М(Х,и) = (P,i);

• (а, Ху, я) * (а', у, л), если X = aeVT и а = аа', М(а,и) = «выброс»;

• (X, X, л) — завершение работы, при этом М(^Д) = «допуск»;

• иначе — «ошибка».

Цепочка и = FIRST(k,a) носит в работе автомата название «аванцепочка».

Таким образом, для создания алгоритма распознавателя языка, заданного произ­вольной LL(k)-rpaMMaTHKoft, достаточно уметь построить управляющую табли­цу М. Управляющую таблицу М, а также множества FIRST и FOLLOW можно получить на основе правил исходной грамматики. Методы построения этой таб­лицы для к>1 в данном пособии не рассматриваются, с ними можно ознакомить­ся в работах [5, 6, т. 1, 65].

При к= 1 все существенно проще. Методы построения для LL(1)-грамматик, а также проверки принадлежности грамматики к классу LL(l)-rpaMMaTHK рас­смотрены ниже.

Алгоритм разбора для Щ1)-грамматик

Для LL(l)-rpaMMaTHK алгоритм работы распознавателя предельно прост. Он за­ключается всего в двух условиях, проверяемых на шаге выбора альтернати­вы. Исходными данными для этих условий являются символ aeVT, обозревав-мый считывающей головкой МП-автомата (текущий символ входной цепочки), и символ AeVN, находящийся на верхушке стека автомата¹. Эти условия можно сформулировать так:

□ необходимо выбрать в качестве альтернативы правило А->х, если

aeFIRST(l,x);

□ необходимо выбрать в качестве альтернативы правило А-+Х, если aeFOLLOW(l,A).

Если ни одно из этих условий не выполняется (нет соответствующих правил), то цепочка не принадлежит заданному языку и МП-автомат не принимает ее (алго­ритм должен сигнализировать об ошибке). Работа автомата на шаге «выброса» остается без изменений. Кроме того, чтобы убедиться, является ли заданная грамматика G(VT,VN,P,S) ЬЦ1)-грамматикой, необходимо и достаточно проверить следующее условие: для каждого символа AeVN, для которого в грамматике существует более одного правила вида А -> а^агЩйп, должно выполняться требование

FIRST(l,OiFOLLOW(l,A)) n FIRST(l,<XjFOLLOW(l,A)) = 0

Vi*j,n>i>0, n>j>0. Очевидно, что если для символа AeVN отсутствует правило вида А-»Х., то соглас­но этому требованию все множества FIRST(l,a₁), FIRST(l,a₂), ..., FIRST(l,a_n) должны попарно не пересекаться, если же присутствует правило А-Л, то они не должны также пересекаться со множеством FOLLOW(l,A). Отсюда видно, что ЬЦ1)-грамматика не может содержать для одного и того же нетерминального символа AeVN двух правил, начинающихся с одного и того же терминального символа.

Условие, накладываемое на правила ЬЦ1)-грамматики, является довольно жест­ким. Очень немногие реальные грамматики могут быть отнесены к классу LL(1)-грамматик. Например, даже довольно простая грамматика G({a},{S}, {S-»a|aS}, S) не удовлетворяет этому условию (хотя она является ЬЦ2)-грамматикой и даже регулярной праволинейной грамматикой).

Иногда удается преобразовать правила грамматики так, чтобы они удовлетворя­ли требованию LL(1)-грамматик. Например, приведенная выше грамматика мо-

Может показаться, что класс ЬЦ1)-грамматик соответствует классу грамматик, анализи­руемых методом рекурсивного спуска, где выбор альтернативы также основан на теку­щем символе входной цепочки. На самом деле это не так — класс LL(1)-грамматик является более широким, чем класс грамматик, анализируемым методом рекурсивно­го спуска. Любая грамматика, анализируемая методом рекурсивного спуска, является ЬЦ1)-грамматикой, но не наоборот: существуют ЬЦ1)-грамматики, которые напрямую методом рекурсивного спуска не анализируются. Дело в том, что распознаватель на базе ЬЦ1)-грамматики (который основан на множествах FIRST и FOLLOW) при выборе альтернативы фактически анализирует не одно, а сразу несколько правил, связанных с текущим символом на верхушке стека, в то время как рекурсивный спуск основан на ана­лизе только одного правила, непосредственно относящегося к этому символу. жет быть преобразована к виду G'({a},{S,A}, {S-»aA, A—>X,|S}, S)¹. В такой форме она уже является LL(1)-грамматикой (это можно проверить). Но формальной метода преобразовать произвольную КС-грамматику к виду LL(1)-грамматик! или убедиться в том, что такое преобразование невозможно, не существует. Пер вое преобразование правил грамматики, которое можно рекомендовать, — устра нение левой рекурсии². Второе преобразование носит название «левая фактори зация», оно уже было упомянуто выше при знакомстве с методом рекурсивной спуска. Это преобразование заключается в следующем: если для символа AeV> существует ряд правил

A->ap₁|ap₂|...|ap_n|YilY2l-L- Vi: p_ie(VTuVN)*, Vj: _7je(VTuVN)*, aeVT

и ни одна цепочка символов _7j не начинается с символа а, тогда во множество не­терминальных символов грамматики VN добавляется новый символ А', а прави­ла для А и А' записываются следующим образом: А—>аА.' jy _t |у₂|- - -1 Ym ^и A'->Pi|p₂|...|p_n Левую факторизацию можно применять к правилам грамматики несколько раз с целью исключить для каждого нетерминального символа правила, начинающие­ся с одних и тех же терминальных символов. Однако применение этих двух пре­образований отнюдь не гарантирует, что произвольную КС-грамматику удастся привести к виду ЬЬ(1)-грамматики.

Для того чтобы запрограммировать работу МП-автомата, выполняющего разбор входных цепочек символов языка, заданного ЬЦ1)-грамматикой, надо научить­ся строить множества символов FIRST(l,x) и FOLLOW(l,A). Для множества FIRST(l,x) все очевидно, если цепочка х начинается с терминального симво­ла, если же она начинается с нетерминального символа В (х = By, xe(VTuVN)⁺ ye(VTuVN)*), то FIRST(l,x) = FIRST(1,B). Следовательно, для Ы(1)-грамматив остается только найти алгоритм построения множеств FIRST(1,B) и FOLLOW(l,A^ для всех нетерминальных символов A.BeVN.

Исходными данными для этих алгоритмов служат правила грамматики.

Алгоритм построения множества FIRST(1,A)

Алгоритм строит множества FIRST(1,A) сразу для всех нетерминальных сим­волов грамматики G(VT,VN,P,S), AeVN. Для выполнения алгоритма надо пред­варительно преобразовать исходную грамматику G(VT,VN,P,S) в граммати­ку G'(VT,VN',P',S'), не содержащую А,-правил (см. алгоритм преобразования в разделе «Преобразование КС-грамматик. Приведенные грамматики», глава 11). На основании полученной грамматики G' и выполняется построение множеств FIRST(l.A) для всех AeVN (если AeVN, то согласно алгоритму преобразова-

Можно убедиться, что две приведенные грамматики задают один и тот же язык: L(G) = = L(G'). Это легко сделать, поскольку обе они являются не только КС-грамматиками, но и регулярными праволинейными грамматиками. Кроме того, формальное преобразова­ние G' в G существует — достаточно устранить в грамматике G' Pt-правила и цепные пра­вила, и будет получена исходная грамматика G. А вот формального преобразования G в G' нет. В общем случае все может быть гораздо сложнее.

¹ Устранение левой рекурсии — это, конечно, необходимое, но не достаточное условие для преобразования грамматики к виду LL-грамматики. Это будет видно далее из примера.

ния также справедливо AeVN'). Множества строятся методом последовательно­го приближения. Если в результате преобразования грамматики G в граммати­ку G' множество VN' содержит новый символ S', то при построении множества FIRST(1,A) он не учитывается. Алгоритм состоит из нескольких шагов.

Шаг 1. Для всех AeVN: FIRST₀(1,A) = {X | А->Ха е Р, Xe(VTuVN), ae(VTuVN)*} (первоначально вносим во множество первых символов для каждого нетерми­нального символа А все символы, стоящие в начале правых частей правил для этого символа A); i:=0.

Шаг 2. Для всех AeVN: FIRST_i+1(l,A) = FIRSTj(l,A) и FIRST^LB), для всех не­терминальных символов Be(FIRSTi(l,A) n VN).

Шаг 3. Если 3 AeVN: FIRST_i+1(l,A) * FIRSTj(l,A), то 1:4+1 и вернуться к шагу 2, иначе перейти к шагу 4.

Шаг 4. Для всех AeVN: FIRST(1,A) = FIRSTi(l,A) \ VN (исключаем из постро­енных множеств все нетерминальные символы).

Алгоритм построения множества FOLLOW(1,A)

Алгоритм строит множества FOLLOW(l,A) сразу для всех нетерминальных сим­волов грамматики G(VT,VN,P,S), AeVN. Для выполнения алгоритма предвари­тельно надо построить все множества FIRST(1,A), V AeVN. Множества строят­ся методом последовательного приближения. Алгоритм состоит из нескольких шагов.

Шаг 1. Для всех AeVN: FOLLOW₀(1,A) - {X | 3 В-ххАХр е Р, BeVN, Xe(VTuVN), a,pe(VTuVN)*} (первоначально вносим во множество последующих символов для каждого нетерминального символа А все символы, которые в правых частях правил встречаются непосредственно за символом A); i:=0. Шаг 2. FOLLOW₀(1,S) = FOLLOW₀(1,S) u {1} (вносим пустую цепочку во мно­жество последующих символов для целевого символа S — это означает, что в конце разбора за целевым символом цепочка кончается, иногда для этой цели используется специальный символ конца цепочки: 1_к).

Шаг 3. Для всех AeVN: FOLLOW; (1,A) = FOLLOWj(l,A) u FIRST(1,B), для всех нетерминальных символов Be(FOLLOWj(l,A) n VN). Шаг 4. Для всех AeVN: FOLLOW", (1,A) = FOLLOW'i(l,A) u FOLLOW^l.B). для всех нетерминальных символов Be(FOLLOW'j(l,A) n VN) и существует пра­вило В-»А..

Шаг 5. Для всех AeVN: FOLLOW_i+1(l,A) = FOLLOW"j(l,A) U FOLLOW"j(l,B). для всех нетерминальных символов BeVN, если существует правило В-»аА, ae(VTuVN)*.

Шаг 6. Если 3 AeVN: FOLLOW_i+1(l,A) ф FOLLOW^l.A), то i:=i+l и вернуться к шагу 3, иначе перейти к шагу 7.

Шаг 7. Для всех AeVN: FOLLOW(l,A) = FOLLOWj(l,A) \ VN (исключаем из построенных множеств все нетерминальные символы).

Пример построения распознавателя для Щ1)-грамматики

Рассмотрим в качестве примера грамматику G({+,-,/,*,а,b}, {S,R,T,F,E}, P, S) с правилами:

Р:

S -> Т | TR

R -> +Т | -Т | +TR | -TR

Т ~> Е | EF

F -> *Е | /Е | *EF | /EF

Е -> (S) | а | b

Это нелеворекурсивная грамматика для арифметических выражений (ранее она была построена в разделе «Распознаватели КС-языков с возвратом», глава 11). Эта грамматика не является ЕЕ(1)-грамматикой. Чтобы убедиться в этом, доста­точно обратить внимание на правила для символов R и F — для них имеется по два правила, начинающихся с одного и того же терминального символа. Преобразуем ее в другой вид, добавив ^-правила. В результате получим новую грамматику G'({+.-,/,*,а,b}, {S,R,T,F,E}, P', S) с правилами:

Р':

S -> TR

R -» X | +TR | -TR

Т -> EF

F 1> X | *EF | /EF

Е -> (S) | а | Ь

Построенная грамматика G' эквивалентна исходной грамматике G. В этом мож­но убедиться, если воспользоваться алгоритмом устранения ^.-правил из разде­ла «Преобразование КС-грамматик. Приведенные грамматики», глава 11. Приме­нив его к грамматике G', получим грамматику G, а по условиям данного алгорит­ма L(G') = L(G). Таким образом, мы получили эквивалентную грамматику, хотя она и построена неформальным методом (следует помнить, что не существует формального алгоритма, преобразующего произвольную КС-грамматику в LL(k)-грамматику для заданного к).

Эта грамматика является ЕЕ(1)-грамматикой. Чтобы убедиться в этом, построим множества FIRST и FOLLOW для нетерминальных символов этой грамматики (поскольку речь заведомо идет об LL(1)-грамматике, цифру «1» в обозначении множеств опустим для сокращения записи).

Для построения множества FIRST будем использовать исходную грамматику G, так как именно она получается из G' при устранении Я,-правил. Построение множеств FIRST.

Шаг 1. FIRSTo(S) = {Т}; FIRSTo(R) = {+,-}; FIRSTo(T) = {E}; FIRSTo(F) = {*,/};

FIRSTo(E) = {(,a,b};

i = 0. Шаг 2. FIRSTj(S) - {Т,Е};

FIRSTAR) = {+,-};

FIRSTt(T) = {E,(,a,b};

FIRST^F) = {*,/};

FIRST^E) = {(,a,b}. Шаг 3. i = 1, возвращаемся к шагу 2. Шаг 2. FIRST₂(S) - {T,E,(,a,b};

FIRST₂(R) = {+,-};

FIRST₂(T) = {E,(,a,b};

FIRST₂(F) = {*,/};

FIRST₂(E) = {(,a,b}. Шаг 3- i = 2, возвращаемся к шагу 2. Шаг 2. FIRST₃(S) - {T,E,(,a,b};

FIRST₃(R) = {+,-};

FIRST₃(T) = {E,(,a,b};

FIRST₃(F) = {*,/};

FIRST₃(E) = {(,a,b}. Шаг 3. i = 2, переходим к шагу 4. Шаг 4. FIRST(S) = {(,a,b};

FIRST(R) = {+,-};

FIRST(T) = {(,a,b};

FIRST(F) = {*,/};

FIRST(E) - {(,a,b}.

Построение закончено. Построение множества FOLLOW.

FOLLOW0(S) -	mi
FOLLOWq(R) ■	-0;
FOLLOWq(T) ■	- {R};
FOLLOWq(F) ■	= 0;
FOLLOW0(E) ■ i-0. FOLLOW0(S) •	= {F};
	• Ш
FOLLOW0(R) ■	= 0;
FOLLOWq(T) ■	= {R};
FOLLOWq(F) =	= 0;
FOLLOW0(E) -	= {F}.

ШагЗ. FOLLOW'₀(S) = {)Д};

FOLLOW'o(R) = 0;

FOLLOW'₀(T) = {R,+,-};

FOLLOW'₀(F) = 0;

FOLLOW'₀(E) = {FA/}. Шаг 4. FOLLOW'o(S) = {)Д};

FOLLOWER) = 0;

FOLLOW"₀(T) = {R,+,-};

FOLLOW"₀(F) = 0;

FOLLOW'o(E) = {FA/}. Шаг 5. FOLLOW^S) = {)Д};

FOLLOWER) = {)Л};

FOLLOW^T) = {R,+,-};

FOLLOW^F) = {R,+,-};

FOLLOW^E) = {F,*,/}. Шаг 6. i = 1, возвращаемся к шагу 3. Шаг 3. FOLLOW'^S) - {Щ

FOLLOWER) = {)Л};

F0LL0W'1(T) = {R,+,-};

FOLLOW',^) * {R,+ -};

FOLLOW'^E) = {F ,*,/}. Шаг 4. FOLLOW'^S) = {)Д};

FOLLOWER) = {)Л};

FOLLOW",(T) = {R,+,-,),M;

FOLLOW",(F) - {R,+ -,)Л};

FOLLOW"i(E) = {F,RV,+,-)Л}-Шаг 5. FOLLOW₂(S) = {)Д};

FOLLOW₂(R) = {)Л|;

FOLLOW₂(T) = {R.+ -, )Л};

FOLLOW₂(F) = {R,+,-,U};

FOLLOW₂(E) = {F,R,*,/,+ -,),M. Шаг 6. i = 2, возвращаемся к шагу 3. Шаг 3. FOLLOW'₂(S) - {)Л};

FOLLOW'₂(R) = {)Д};

FOLLOW'₂(T) = {R,+ ,-,),*.};

FOLLOW'₂(F) = {R,+,-,),M;

FOLLOW'₂(E) = {F,R,*,/,+,-,),A.}.

Шаг 4. FOLLOW"₂(S) - {)Д};

FOLLOWER) - {)Д};

FOLLOW"₂(T) - {R,+,-)M

FOLLOW"₂(F) = {R,+,-,)Д};

FOLLOW"₂(E) = {F,RA/>+-,)ЛЬ Шаг 5. FOLLOW₃(S) = {)Д};

FOLLOW₃(R) - {),%};

FOLLOW₃(T) = \R,+-,)Д};

FOLLOW₃(F) = {ЕЯ-)Д};

FOLLOW₃(E) = {F,R, *,/,+~,)Д}-Шаг 6. i = 2, переходим к шагу 7. Шаг 7. FOLLOW(S) - {)Д};

FOLLOW(R) = ОД};

FOLLOW(T) f {+,-,)Д};

FOLLOW(F) - {+,-,)Д};

FOLLOW(E) = {*,/,+,-,)Д}.

Построение закончено.

В результате выполненных построений можно видеть, что необходимое и доста­точное условие принадлежности КС-грамматики к классу ЪЦ1)-грамматик вы­полняется.

Построенные множества FIRST и FOLLOW можно представить в виде таблицы. Результат выполненных построений отражает табл. 12.1.

Таблица 12.1.	Множества FIRST и FOLLOW для грамматики G'
Символ AeVN		FIRST(1 ,A)	FOLLOW(1 ,A)
S		(ab	)i
R		+ -	ух
Т		(ab	+ -)Х
F		V	+ -)Х
Е		(ab	* / + - ) X

Рассмотрим работу распознавателя. Ход разбора будем отражать по шагам рабо­ты автомата в виде конфигурации МП-автомата, к которой добавлена цепочка, содержащая последовательность примененных правил грамматики. Состояние автомата q, указанное в его конфигурации, можно опустить, так как оно единст­венное: (a, Z, у), где а — непрочитанная часть входной цепочки символов; Z — содержимое стека (верхушка стека находится слева); у — последовательность но­меров примененных правил (последовательность дополняется слева, так как ав­томат порождает левосторонний вывод). Примем, что правила в грамматике номеруются в порядке слева направо и сверху вниз. На основе номеров примененных правил при успешном завершении разбо ра можно построить цепочку вывода и дерево вывода.

В качестве примера возьмем две правильные цепочки символов а+а*Ь и (a+a)*b i две ошибочные цепочки символов а+а* и (+а)*Ь. Разбор цепочки а+а*Ь.

1. (а+_а*Ь, БД)

2. (a+a*b, TR, 1), так как aeFIRST(l,TR)

3. (a+a*b, EFR, 1,5), так как aeFIRST(l,EF)

4. (a+a*b, aFR, 1,5,10), так как aeFIRST(l,a)

5. (+a*b, FR, 1,5,10)

6. (+a*b, R, 1,5,10,6), так как +eFOLLOW(l,F)

7. (+a*b, +TR, 1,5,10,6,3), так как +eFIRST(l,+TR)

8. (a*b, TR, 1,5,10,6,3)

9. (a*b, EFR, 1,5,10,6,3,5), так как aeFIRST(l,EF) 10. (a*b,aFR, 1,5,10,6,3,5,10), так как a₆FIRST(l,a) И. (*b, FR, 1,5,10,6,3,5,10)

12. (*b, *EFR, 1,5,10,6,3,5,10,7), так как *eFIRST(l,*EF)

13. (b, EFR, 1,5,10,6,3,5,10,7)

14. (b, bFR, 1,5,10,6,3,5,10,7,11), так как beFIRST(l,b)

15. (X, FR, 1,5,10,6,3,5,10,7,11)

16. (X, R, 1,5,10,6,3,5,10,7,11,6), так как ?i6F0LL0W(l,F)

17. (X, X, 1,5,10,6,3,5,10,7,11,6,2), так как keFOLLOW(l,R), разбор закончен. Це почка принимается.

Получили цепочку вывода:

S => TR => EFR => aFR => aFR => aR => a+TR => a+EFR => a+aFR => a+a*EFR => a+_a*bFR => a+a*bR => a+a*b

Соответствующее ей дерево вывода приведено на рис. 12.2. Разбор цепочки (а+а)*Ь.

1. ((a+a)*b, S, Я.)

2. ((a+a)*b, TR, 1), так как (eFIRST(l.TR)

3. ((a+a)*b, EFR, 1,5), так как (eFIRST(l,EF)

4. ((a+a)*b, (S)FR, 1,5,9), так как (eFIRST(l,(S))

5. (a+a)*b, S)FR, 1,5,9)

6. (a+a)*b, TR)FR, 1,5,9,1), так как aeFIRST(i.TR)

7. (a+a)*b, EFR)FR, 1,5,9,1,5), так как aeFIRST(l,EF)

8. (a+a)*b, aFR)FR, 1,5,9,1,5,10), так как aeFIRST(i,a)

(+a)*b, FR)FR, 1,5,9,1,5,10)

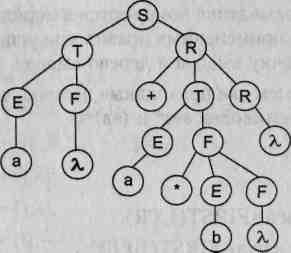
Рис. 12.2. Дерево вывода в Щ1)-грамматике для цепочки «а+а*Ь»

10. (+a)*b, R)FR, 1,5,9,1,5,10,6), так как +<=FOLLOW(l,F)

11. (+a)*b, +TR)FR, 1,5,9,1,5,10,6,3), так как +eFIRST(l,+TR)

12. (a)*b, TR)FR, 1,5,9,1,5,10,6,3)

13. (a)*b, EFR)FR, 1,5,9,1,5,10,6,3,5), так как aeFIRST(l,EF)

14. (a)*b, aFR)FR, 1,5,9,1,5,10,6,3,5,10), так как aeFIRST(l,a)

15. (q,)*b, FR)FR, 1,5,9,1,5,10,6,3,5,10)

16. ()*b, R)FR, 1,5,9,1,5,10,6,3,5,10,6), так как )eFOLLOW(l,F)

17. ()*b, )FR, 1,5,9,1,5,10,6,3,5,10,6,2), так как )eFOLLOW(l,R)

18. (*b, FR, 1,5,9,1,5,10,6,3,5,10,6,2)

19. (*b, *EFR, 1,5,9,1,5,10,6,3,5,10,6,2,7), так как *eFOLLOW(l,*EF)

20. (b, EFR, 1,5,9,1,5,10,6,3,5,10,6,2,7)

21. (b, bFR, 1,5,9,1,5,10,6,3,5,10,6,2,7,11), так как beFIRST(l,b)

22. (X, FR, 1,5,9,1,5,10,6,3,5,10,6,2,7,11)

23. (X, R, 1,5,9,1,5Д0,6,3,5Д0Д2,7,11,6), так как Хе FOLLOW(l.F)

24. (X, X, 1,5,9,1,5,10,6,3,5,10,6,2,7,11,6,2), так как ?ieFOLLOW(l,R), разбор закон­чен. Цепочка принимается.

Получили цепочку вывода:

S => TR => EFR => (S)FR =} (TR)FR => (EFR)FR => (aFR)FR => (aR)FR => (a+TR)FR => (a+EFR)FR =» (a+aFR)FR s» (a+aR)FR => (a+a)FR => (a+a)*EFR => (a+a)*bFR => (a+a)*bR => (a+a)*b

Соответствующее ей дерево вывода приведено на рис. 12.3. Разбор цепочки а+а*.

1. (а+а*, S, X)

2. (а+а*, TR, 1), так как aeFIRST(l.TR)

3. (а+а*, EFR, 1,5), так как aeFIRST(l.EF)

4. (а+а*, aFR, 1,5,10), так как aeFIRST(l.a)

(+а*, FR, 1,540)

s

© sx © © © лЗ

(© ©>■>. (ь) (х)

© © © Jj) (я)

© © © © ©

Рис. 12.3. Дерево вывода в Щ1)-грамматике для цепочки <<(а+а)*Ь»

6. (+а*, R, 1,5,10,6), так как +eFOLLOW(l,F)

7. (+а*, +TR, 1,5,10,6,3), так как +eFIRST(l,+TR)

8. (a*, TR, 1,5,10,6,3)

9. (a*, EFR, 1,5,10,6,3,5), так как a_eFIRST(l,EF) 10. (a*, aFR, 1,5,10,6,3,5,10), так как aeFIRST(l,a) И. (*, FR, 1,5,10,6,3,5,10)

12. (*, *EFR, 1,5,10,6,3,5,10,7), так как *eFIRST(l,*EF)

13. (X, EFR, 1,5,10,6,3,5,10,7)

14. Ошибка, так как A,eFOLLOW(l,E), но нет правила вида Е->Х. Цепочка i принимается.

Разбор цепочки (+а)*Ь.

1. ((+a)*b,S,V)

2. ((+a)*b, TR, 1), так как (eFIRST(l,TR)

3. ((+a)*b, EFR, 1,5), так как (eFIRST(l,EF)

4. ((+a)*b, (S)FR, 1,5,9), так как (eFIRST(l,(S))

5. (+a)*b, S)FR, 1,5,9)

6. Ошибка, так как нет правил для S вида S-»a таких, чтобы +eFIRST(l,c и +gFOLLOW(l,S). Цепочка не принимается.

Из рассмотренных примеров видно, что алгоритму разбора цепочек, построе] ному на основе распознавателя для LL(1)-грамматик, требуется гораздо меньн шагов на принятие решения о принадлежности цепочке языку, чем рассмотре] ному выше алгоритму разбора с возвратами. Надо отметить, что оба алгоритл распознают цепочки одного и того же языка. Данный алгоритм имеет большу эффективность, поскольку при росте длины цепочки количество шагов его ра

тет линейно, а не экспоненциально. Кроме того, ошибка обнаруживается этим алгоритмом сразу, в то время как разбор с возвратами будет просматривать для неверной входной цепочки возможные варианты до конца, пока не переберет их все.

Очевидно, что этот алгоритм является более эффективным, но жесткие ограни­чения на правила для ЬЦ1)-грамматик сужают возможности его применения.

Восходящие распознаватели КС-языков без возвратов

Определение 1.Щк)-грамматики

Восходящие распознаватели выполняют построение дерева вывода снизу вверх. Результатом их работы является правосторонний вывод. Функционирование таких распознавателей основано на модификациях алгоритма «сдвиг-свертка» (или «перенос-свертка»), который был рассмотрен в разделе «Распознаватели КС-языков с возвратом», глава 11.

Идея состоит в том, чтобы модифицировать этот алгоритм таким образом, чтобы на каждом шаге его работы можно было однозначно дать ответ на следующие во­просы:

• что следует выполнять: сдвиг (перенос) или свертку;

• какую цепочку символов а выбрать из стека для выполнения свертки;

• какое правило выбрать для выполнения свертки (в том случае, если сущест­вует несколько правил вида A_t-»a, A₂->a, ... А_п-ж).

Тогда восходящий алгоритм распознавания цепочек КС-языка не требовал бы выполнения возвратов, поскольку сам язык мог бы быть задан детерминирован­ным расширенным МП-автоматом. Конечно, как уже было сказано, это нельзя сделать в общем случае, для всех КС-языков (поскольку даже сам класс детер­минированных КС-языков более узкий, чем весь класс КС-языков). Но, вероят­но, среди всех КС-языков можно выделить такой класс (или классы), для кото­рых подобная реализация распознающего алгоритма станет возможной.

В первую очередь можно использовать тот же самый подход, который был поло­жен в основу определения LL(k)-грамматик. Тогда мы получим другой класс КС-грамматик, который носит название LR(k)-грамматик.

КС-грамматика обладает свойством LR(k), k>0, если на каждом шаге выво­да для однозначного решения вопроса о выполняемом действии в алгоритме «сдвиг-свертка» («перенос-свертка») расширенному МП-автомату достаточно знать содержимое верхней части стека и рассмотреть первые к символов от те­кущего положения считывающей головки автомата во входной цепочке сим­волов.

Грамматика называется LR(k)-грамматикой, если она обладает свойством LR(k^ для некоторого к^О¹.

Название «LR(k)>>, как и рассмотренное выше «LL(k)», также несет определен­ный смысл. Первая литера «L» также обозначает порядок чтения входной цепоч­ки символов: слева— направо. Вторая литера «R» происходит от слова «right» и по аналогии с LL(k), означает, что в результате работы распознавателя получа ется правосторонний вывод. Вместо «к» в названии грамматики стоит число, ко торое показывает, сколько символов входной цепочки надо рассмотреть, чтобь принять решение о действии на каждом шаге алгоритма «сдвиг-свертка». Так существуют ]Л(0)-грамматики, 1^(1)-грамматики и другие классы.

В совокупности все 1Л(к)-грамматики для всех к>0 образуют класс LR-грамма тик.

На рис. 12.4 схематично показано частичное дерево вывода для некоторой LR(k) грамматики. В нем со обозначает уже разобранную часть входной цепочки а, н: основе которой построена левая часть дерева у. Правая часть дерева х — это ещ> не разобранная часть, а А — это нетерминальный символ, к которому на очеред ном шаге будет свернута цепочка символов z, находящаяся на верхушке стек; МП-автомата. В эту цепочку уже входит прочитанная, но еще не разобранна; часть входной цепочки и. Правая часть дерева х будет построена на основе част] входной цепочки х. Свойство LR(k) предполагает, что однозначный выбор дей ствия, выполняемого на каждом шаге алгоритма «сдвиг-свертка», может быт: сделан на основе цепочки и и к первых символов цепочки т., являющихся часть» входной цепочки а. Этим очередным действием может быть свертка цепочки z к сим волу А или перенос первого символа из цепочки т. и добавление его к цепочке г.

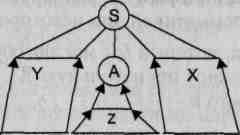
со и | т

к a Рис. 12.4. Схема построения дерева вывода для 1Я(к)-грамматики

Рассмотрев схему построения дерева вывода для 1^(к)-грамматики на рис. 12. и сравнив ее с приведенной выше на рис. 12.1 схемой для ЬЦк)-грамматию

Существование Ы1(0)-грамматик уже не является бессмыслицей в отличие от LL(0 грамматик. В данном случае используется расширенный МП-автомат, который анализ! рует не один, а сразу несколько символов, находящихся на верхушке стека. Причем сред этих символов могут быть и терминальные символы из входной цепочки, попавшие стек при выполнении сдвигов (переносов). Поэтому даже если автомат при к = 0 и не б; дет смотреть на текущий символ входной цепочки, построенный им вывод все равно б; дет зависеть от содержимого стека, а значит, и от содержимого входной цепочки.

можно предположить, что класс LR-грамматик является более широким, чем класс LL-грамматик. Основанием для такого предположения служит тот факт, что на каждом шаге работы распознавателя Ы1(к)-грамматики обрабатывается больше информации, чем на шаге работы распознавателя ЬЦк)-грамматики. Действительно, для принятия решения на каждом шаге алгоритма распознава­ния LL(k)-грамматики используются первые к символов из цепочки от, а для принятия решения на шаге распознавания ЬЫ(к)-грамматики — вся цепочка и и еще первые к символов из цепочки т. Очевидно, что во втором случае можно проанализировать больший объем информации и, таким образом, построить вы­вод для более широкого класса КС-языков.

Приведенное выше довольно нестрогое утверждение имеет строго обоснованное доказательство. Доказано, что класс LR-грамматик является более широким, чем класс LL-грамматик [6, т. 2]. То есть для каждого КС-языка, заданного LL-грам-матикой, может быть построена LR-грамматика, задающая тот же язык, но не на­оборот. Существуют также языки, заданные LR-грамматиками, для которых не­возможно построить LL-грамматику, задающую тот же язык. Иначе говоря, для всякой LL-грамматики существует эквивалентная ей LR-грамматика, но не для всякой LR-грамматики существует эквивалентная ей LL-грамматика¹. Для LR(k)-rpaMMaTHK известны следующие полезные свойства:

• всякая LR(k)-rpaMMaTHKa для любого к > О является однозначной;

• существует алгоритм, позволяющий проверить, является ли заданная грамма­тика LR(k)-rpaMMaTHKoft для строго определенного числа к.

Есть, однако, неразрешимые проблемы для произвольных КС-грамматик (они аналогичны таким же проблемам для других классов КС-грамматик):

• не существует алгоритма, который бы мог проверить, является ли заданная КС-грамматика LR(k)-rpaMMaraKoft для некоторого произвольного числа к;

• не существует алгоритма, который бы мог преобразовать (или доказать, что преобразование невозможно) произвольную КС-грамматику к виду LR(k)-грамматики для некоторого к.

Кроме того, для LR-грамматик доказано еще одно очень интересное свойство — класс LR-грамматик полностью совпадает с классом детерминированных КС-языков. То есть, во-первых, любая LR(k)-rpaMMaraKa задает детерминированный КС-язык (это очевидно следует из однозначности всех LR-грамматик), а во-вто­рых, для любого детерминированного КС-языка можно построить LR-граммати-ку, задающую этот язык. Второе утверждение уже не столь очевидно, но доказа­но в теории формальных языков [6, т. 1, 65]².

¹ Говоря о соотношении классов LL-грамматик и LR-грамматик, мы не затрагиваем вопрос о значениях к для этих грамматик. Если для некоторой LL(k)-rpaMMaraKH всегда сущест­ вует эквивалентная ей LR-грамматика, то это вовсе не значит, что она будет LR(k)-rpaM- матикой с тем же значением к, и наоборот. Но если говорится, что существуют LR- грамматики, для которых нет эквивалентных им LL-грамматик, то это означает, что нет эквивалентных им LL(k)-rpaMMaraK для всех возможных значений к>0.

² Более того, доказано даже, что любой детерминированный КС-язык может быть задан LR( 1 )-грамматикой. В принципе класс LR-грамматик очень удобен для построения распознавате; детерминированных КС-языков (а все языки программирования, безуслов относятся к этому классу). Но тот факт, что для каждого детерминирован» КС-языка существует задающая его LR-грамматика, еще ни о чем не говорит, ] скольку из-за неразрешимости проблемы преобразования отсутствует алгори который позволил бы эту грамматику построить всегда. Данный детермини ванный КС-язык может быть изначально задан грамматикой, которая не on сится к классу LR-грамматик. В таком случае совсем не очевидно, что для эт( языка удастся построить распознаватель на основе LR-грамматики, потому > в общем случае нет алгоритма, который бы позволил эту грамматику получк хотя и известно, что она существует. То, что проблема не разрешима в оби случае, совсем не означает, что ее не удастся решить в конкретной ситуац И здесь факт существования LR-грамматики для каждого детерминирован» КС-языка играет важную роль — всегда есть смысл в каждом конкретном слу пытаться построить такую грамматику.

Принципы построения распознавателей для LR(k)-rpaMMaTHK

Для того чтобы формально определить LR(k) свойство для КС-грамматик, в дем понятие пополненной КС-грамматики. Грамматика G' является пополн ной грамматикой, построенной на основании исходной грамматики G(VT,VN,P если выполняются следующие условия:

• грамматика G' совпадает с грамматикой G, если целевой символ S не ветре ется нигде в правых частях правил грамматики G;

• грамматика G' строится как грамматика G'(VT,VNu{S'},Pu{S'-»S},S'), если левой символ S встречается в правой части хотя бы одного правила из мно: ства Р в исходной грамматике G.

Фактически пополненная КС-грамматика строится таким образом, чтобы ее левой символ не встречался в правой части ни одного правила. Если нужно, в исходную грамматику G для этого добавляется новый терминальный сим! S', который становится целевым символом, и новое правило S'-»S. Очевид что пополненная грамматика G' эквивалентна исходной грамматике G, то е L(G') = L(G).

Теперь рассмотрим формальное определение LR(k) свойства.

Если для произвольной КС-грамматики G в ее пополненной грамматике G'; двух произвольных цепочек вывода из условий:

1. S' =>* aAw => aPw

2. S' =>* уВх У ару

3. FIRST(k,w) - FIRST(k,y)

следует, что aAw = уВх (то есть а = у, А = В и х = у), то доказано, что грамма ка G обладает LR(k) свойством. Очевидно, что тогда и пополненная грамма ка G' также обладает LR(k) свойством.

Понятие «пополненной грамматики» введено исключительно с той целью, чтобы в процессе работы алгоритма «сдвиг-свертка» выполнение свертки к целевому символу пополненной грамматики S' служило сигналом к завершению алгорит­ма (поскольку в пополненной грамматике символ S' в правых частях правил ни­где не встречается). Если условие отсутствия целевого символа в правых частях правил грамматики не будет соблюдаться, то на алгоритм распознавателя по­требуется наложить дополнительные ограничения, так как появление целевого символа на вершине стека уже не будет означать завершение работы алгоритма. Поскольку построение пополненных грамматик выполняется элементарно и не накладывает никаких дополнительных ограничений на исходную КС-граммати­ку, то дальше будем считать, что все распознаватели для Ь11(к)-грамматик рабо­тают с пополненными грамматиками.

Распознаватель для Ы1(к)-грамматик функционирует на основе управляющей таблицы Т. Эта таблица состоит из двух частей, называемых «действия» и «пере­ходы». По строкам таблицы распределены все цепочки символов на верхушке стека, которые могут приниматься во внимание в процессе работы распознавате­ля. По столбцам в части «действия» распределены все части входной цепочки символов длиной не более к (аванцепочки), которые могут следовать за считы­вающей головкой автомата в процессе выполнения разбора; а в части «перехо­ды» — все терминальные и нетерминальные символы грамматики, которые мо­гут появляться на верхушке стека автомата при выполнении действий (сдвигов или сверток).

Клетки управляющей таблицы Т в части «действия» содержат следующие дан­ные:

• «сдвиг» — если в данной ситуации требуется выполнение сдвига (переноса те­кущего символа из входной цепочки в стек);

• «успех» — если возможна свертка к целевому символу грамматики S и разбор входной цепочки завершен;

• целое число («свертка») — если возможно выполнение свертки (число обо­значает номер правила грамматики, по которому должна выполняться сверт­ка);

• «ошибка» — во всех других ситуациях.

Действия, выполняемые распознавателем, можно вычислять всякий раз на осно­ве состояния стека и текущей аванцепочки. Однако этого вычисления можно из­бежать, если после выполнения действия сразу же определять, какая строка таб­лицы Т будет использована для выбора следующего действия. Тогда эту строку можно поместить в стек вместе с очередным символом и выбирать затем в мо­мент, когда она понадобится. Таким образом, автомат будет хранить в стеке не только символы алфавита, но и связанные с ними строки управляющей табли­цы Т.

Клетки управляющей таблицы Т в части «переходы» как раз и служат для выяс­нения номера строки таблицы, которая будет использована для определения вы­полняемого действия на очередном шаге. Эти клетки содержат следующие дан­ные:

• целое число — номер строки таблицы Т;

• «ошибка» — во всех других ситуациях.

Для удобства работы распознаватель Ы1(к)-грамматики использует также два cni циальных символа -L_H и J__K. Считается, что входная цепочка символов всегда н; чинается символом _1__я и завершается символом 1_к. Тогда в начальном состояни работы распознавателя символ 1_н находится на верхушке стека, а считывающг головка обозревает первый символ входной цепочки. В конечном состоянии стеке должны находиться символы S (целевой символ) и 1„, а считывающая п ловка автомата должна обозревать символ -L_K.

Алгоритм функционирования распознавателя Ы1(к)-грамматики можно описа! следующим образом:

Шаг 1. Поместить в стек символ ±_н и начальную (нулевую) строку управляюще таблицы Т. В конец входной цепочки поместить символ 1_к. Перейти к шагу 2.

Шаг 2. Прочитать с вершины стека строку управляющей таблицы Т. Выбрать i этой строки часть «действие» в соответствии с аванцепочкой, обозреваемой сч] тывающей головкой автомата. Перейти к шагу 3.

Шаг 3. В соответствии с типом действия выполнить выбор из четырех вариантов

• «сдвиг» — если входная цепочка не прочитана до конца, прочитать и запо1 нить как «новый символ» очередной символ из входной цепочки, сдвину считывающую головку на одну позицию вправо, иначе прервать выполнен] алгоритма и сообщить об ошибке;

• целое число («свертка») — выбрать правило в соответствии с номером, уд лить из стека цепочку символов, составляющую правую часть выбранно правила, взять символ из левой части правила и запомнить его как «новь символ»;

• «ошибка» — прервать выполнение алгоритма, сообщить об ошибке;

• «успех» — выполнить свертку к целевому символу S, прервать выполнен: алгоритма, сообщить об успешном разборе входной цепочки символов, ее. входная цепочка прочитана до конца, иначе сообщить об ошибке.

Конец выбора. Перейти к шагу 4.

Шаг 4. Прочитать с вершины стека строку управляющей таблицы Т. Выбрать этой строки часть «переход» в соответствии с символом, который был запомн как «новый символ» на предыдущем шаге. Перейти к шагу 5.

Шаг 5. Если часть «переход» содержит вариант «ошибка», тогда прервать выпе нение алгоритма и сообщить об ошибке, иначе (если там содержится номер стр ки управляющей таблицы Т) положить в стек «новый символ» и строку табл цы Т с выбранным номером. Вернуться к шагу 2.

Для работы алгоритма кроме управляющей таблицы Т используется также нев торая временная переменная («новый символ»), хранящая значение термина; ного или нетерминального символа, полученного в результате сдвига или све{ ки. В программной реализации алгоритма вовсе не обязательно помещать в ст сами строки управляющей таблицы — поскольку сама таблица неизменна в щ цессе выполнения алгоритма, то достаточно запоминать соответствующие ссылв

Доказано, что данный алгоритм имеет линейную зависимость необходимых для его выполнения вычислительных ресурсов от длины входной цепочки символов. Следовательно, распознаватель для ЬЩк)-грамматики имеет линейную зависи­мость сложности от длины входной цепочки, а потому является линейным рас­познавателем.

Для построения распознавателя осталось научиться строить управляющую таб­лицу Т. Исходными данными для ее построения служат правила исходной грам­матики. Вопросы построения этой таблицы в данном пособии не рассматрива­ются, они достаточно подробно освещены в [6, т. 1]. Далее будут рассмотрены только примеры управляющих таблиц для некоторых достаточно простых грам­матик.

Распознаватель для 1.Р.(0)-грамматики

Простейшим случаем ЬИ(к)-грамматик являются Ы1(0)-грамматики. При к - О распознающий расширенный МП-автомат совсем не принимает во внимание те­кущий символ, обозреваемый его считывающей головкой. Решение о выполняе­мом действии принимается только на основании содержимого стека автомата. При этом не должно возникать конфликтов между выполняемым действием (сдвиг или свертка), а также между различными вариантами при выполнении свертки. Управляющая таблица для Ь11(0)-грамматики строится на основании понятия «левых контекстов» для нетерминальных символов: очевидно, что после выпол­нения свертки для нетерминального символа А в стеке МП-автомата ниже этого символа будут располагаться только те символы, которые могут встречаться в цепочке вывода слева от А. Эти символы и составляют «левый контекст» для А. Поскольку выбор между сдвигом или сверткой, а также между типом свертки в Ь11(0)-грамматиках выполняется только на основании содержимого стека, то Ы1(0)-грамматика должна допускать однозначный выбор на основе левого кон­текста для каждого символа [5, 65, т. 1, 15, 65].

Рассмотрим простую КС-грамматику G({a,b}, {S}, {S-»aSS|b}, S). Пополненная грамматика для нее будет иметь вид G({a,b}, {S, S'}, {S'-»S, S ->aSS|b), $'). Эта грамматика является Ы1(0)-грамматикой. Управляющая таблица для нее приведена в табл. 12.2.

Таблица 12.2. Пример управляющей таблицы для 1_В(0)-грамматики

Стек	Действие	Переход
		S	а	b
1«	сдвиг	1	2	3
S	успех, 1
а	сдвиг	4	2	3
b	свертка, 3
aS	сдвиг	5	2	3
aSS	свертка, 2

Колонка «Стек», присутствующая в таблице, в принципе не нужна для распозь вателя. Она введена исключительно для пояснения каждого состояния сте автомата. Пустые клетки в таблице соответствуют состоянию «ошибка». Праг ла в грамматике пронумерованы от 1 до 3 (при этом будем считать, что состс нию «успех» — свертке к нулевому символу — в пополненной грамматике Bcei соответствует первое правило). Распознаватель работает, невзирая на текущ символ, обозреваемый считывающей головкой расширенного МП-автомата, i этому колонка «Действие» в таблице имеет только один столбец, не помеченш никаким символом, — указанное в ней данное действие выполняется всегда д каждой строки таблицы.

Рассмотрим примеры распознавания цепочек этой грамматики. Работу распоз) вателя будем отображать по шагам. Конфигурацию расширенного МП-автом; будем отображать в виде трех компонентов: не прочитанная еще часть входн цепочки символов, содержимое стека МП-автомата, последовательность номер примененных правил грамматики (поскольку автомат имеет только одно состс ние, его можно не учитывать). В стеке МП-автомата вместе с помещенными tj символами показаны и номера строк управляющей таблицы, соответствуют этим символам в формате {символ, номер строки).

Разбор цепочки abababb.

1. (abababbl_K, {_L_H,0}, X)

2. (bababbl_K, {±„,0}{a,2}, X)

3. (ababbl_K, {±_H,0}{a,2}{b,3}, X)

4. (ababbl_K, {±_H,0}{a,2}{S,4}, 3)

5. (babbl_K, {±_H,0}{a,2}{S,4}{a,2}, 3)

6. (abbl_K, {±,„0}{a,2}{S,4}{a,2}{b_>3}, 3)

7. (abbl_K, {±„,0}{a,2}{S,4}{a,2}{S,4}, 3,3)

8. (bbl_K, {±„,0}{a,2}{S,4}{a,2}{S,4}{a,2}, 3,3)

9. (bl_K, {±,„0}{a,2}{S,4}{a,2}{S,4}{a,2}{b,3}, 3,3)

10. (bl_K, {±_H,0}{a,2}{S,4}{a,2}{S,4}{a,2}{S,4}, 3,3,3)

11. (1_K, {±_H,0}{a,2}{S,4}{a,2}{S,4}{a,2}{S,4}{b,3}, 3,3,3)

12. (1_K, {±_H,0}{a,2}{S,4}{a,2}{S,4}{a,2}{S,4}{S,5}, 3,3,3,3)

13. (1_K, {±„,0}{a,2}{S,4}{a,2}{S,4}{S,5}, 3,3,3,3,2)

14. (J__KI {l„,0}{a,2}{S,4}{S,5}, 3,3,3,3,2,2)

15. (1_K, {±_H,0}{S,1}, 3,3,3,3,2,2,2)

16. (_L_K, {-L_H,0}{S',*}, 3,3,3,3,2,2,2,1) — разбор завершен.

Соответствующая цепочка вывода будет иметь вид (используется правостор* ний вывод): S' => S => aSS => aSaSS => aSaSaSS => aSaSaSb => aSaSabb => aSababb abababb.

Разбор цепочки aabbb.

1. (aabbb-L_K, {±,,,0}, X)

(abbb-L_K, {±,„0}{a,2}, X)

3. (bbbl_K, {1,„0}{а,2}{а,2}, X)

4. (bb±_K, {±_H,0}{a,2}{a,2}{b,3}, X)

5. (bb±_K, {l_H,0}{a,2}{a,2}{S,4}, 3)

6. (bl_K, {l_H,0}{a,2}{a,2}{S,4}{b,3}, 3)

7. (bl_K, {±_H,0}{a,2}{a,2}{S,4}{S,5}, 3,3)

8. (bl_K, {l_H,0}{a,2}{S,4}, 3,3,2)

9. (1_K, {l_H,0}{a,2}{S,4}{b,3}, 3,3,2)

10. (1_K, {l_H,0}{a,2}{S,4}{S,5}, 3,3,2,3)

11. (1_K, {1_H,0}{S,1}, 3,3,2,3,2)

12. (1_K, {1_H,0}{S',*}, 3,3,2,3,2,1) - разбор завершен.

Соответствующая цепочка вывода будет иметь вид (используется правосторон­ний вывод): S' => S => aSS => aSb => aaSSb => aaSbb => aabbb. Разбор цепочки a abb.

1. (aabb±_K, {±„,0}Д)

2. (abbl_K, {l_H,0}{a,2}, X)

3. (bbl_K, {l_H,0}{a,2}{a,2}, X)

4. (bl_K, {l_w0}{a,2}{a,2}{b,3}, X)

5. (bl_K, {±_H,0}{a,2}{a,2}{S,4}, 3)

6. (1_K, {l_H,0}{a,2}{a,2}{S,4}{b,3}, 3)

7. (1_K) {l_H,0}{a,2}{a,2}{S,4}{S,5}, 3,3)

8. (1_K, {l_H,0}{a,2}{S,4}, 3,3,2)

9. Ошибка, невозможно выполнить сдвиг.

Распознаватель для Ы1(0)-грамматики достаточно прост. Приведенный выше пример можно сравнить с методом рекурсивного спуска или с распознавателем для LL(1)-грамматики — оба эти метода применимы к описанной выше грамма­тике. По количеству шагов работы распознавателя эти методы сопоставимы, но по реализации нисходящие распознаватели в данном случае немного проще.

Распознаватель для 1Е(1)-грамматики

Другим употребительным классом LR(k)-грамматик являются LR( ^-граммати­ки. В этих грамматиках основанием для принятия расширенным МП-автоматом решения о выполнении сдвига или свертки служит информация о содержимом стека автомата и текущий символ, обозреваемый считывающей головкой. Рассмотрим простую КС-грамматику G({a,b}, {S}, {S-»SaSb|X}. S). Пополненная грамматика для нее будет иметь вид G({a,b}, {S, S'}. {S'->S, S-»SaSb|X}, S'). Эта грамматика является 1Л(1)-грамматикой [5, 15, 65]. Управляющая таблица для нее приведена в табл. 12.3.

Колонка «Стек», присутствующая в таблице, в принципе не нужна для распозна­вателя. Она введена исключительно для пояснения каждого состояния стека автомата. Пустые клетки в таблице соответствуют состоянию «ошибка». Прави-

ла в грамматике пронумерованы от 1 до 3 (при этом будем считать, что состс нию «успех» — свертке к нулевому символу — в пополненной грамматике всег соответствует первое правило). Колонка «Действие» в таблице содержит пег чень действий, соответствующих текущему входному символу, обозреваемо] считывающей головкой расширенного МП-автомата.

Таблица 12.3. Пример управляющей таблицы для 1.Р(1)-грамматики

Стек	Действие			Переход
	a	Ь	J»	а	b	S
1„	свертка, 3		свертка, 3			1
S	сдвиг		успех, 1	2
Sa	свертка, 3	свертка, 3				3
SaS	сдвиг	сдвиг		4	5
SaSa	свертка, 3	свертка, 3				6
SaSb	свертка, 2		свертка, 2
SaSaS	сдвиг	сдвиг		4	7
SaSaSb	свертка, 2	свертка, 2

Рассмотрим примеры распознавания цепочек этой грамматики по шагам, ко^г рые совершает распознаватель. Конфигурацию расширенного МП-автомата ( дем отображать в виде трех компонентов: не прочитанная еще часть входной ] почки символов, содержимое стека МП-автомата, последовательность номер примененных правил грамматики (поскольку автомат имеет только одно сост< ние, его можно не учитывать). В стеке МП-автомата вместе с помещенными тз символами показаны и номера строк управляющей таблицы, соответствует этим символам в формате {символ, номер строки}.

Разбор цепочки abababb.

1. (abababb±_K, {±„,0}Д)

2. (abababbl_K> {±„,0}{S,1}, 3)

3. (bababbl_K, {l_H,0}{S,l}{a,2}, 3)

4. (bababbl_K, {±_H,0}{S,l}{a,2}{S,3}, 3,3)

5. (ababbl_K, {±„,0}{S,l}{a,2}{S,3}{b,5}, 3,3)

6. (ababbl_K, {±„,0}{S,1}, 3,3,2)

7. (babbl_K, {±_H,0}{S,l}{a,2}, 3,3,2)

8. (babbJL_K, {±_H,0}{S,l}{a,2}{S,3}, 3,3,2,3)

9. (abbl_K, {±_H,0}{S,l}{a,2}{S,3}{b,5}, 3,3,2,3) 10. (abbJ__K, {±„,0}{S,1}, 3,3,2,3,2)

U. (bb±_K, {±_H,0}{S,l}{a,2}, 3,3,2,3,2)

12. (bb±_K, {_L„,0}{S,l}{a,2}{S,3}, 3,3,2,3,2,3)

13. (b±_K, {±_H,0}{S,l}{a,2}{S,3}{b,5}, 3,3,2,3,2,3)

14. Ошибка, нет данных для «Ь» в строке 5.

Разбор цепочки aababb.

1. (aababbl_K, {±_и,0}, к)

2. (aababbl_K, {±„,0}{S,1}, 3)

3. (ababbl_K, {:Ц0}{ЗДаД 3)

4. (ababb±_K, {l_H,0}{S,l}{a,2}{S,3}, 3,3)

5. (babbl_K) {±₁₁,0}{S,l}{a,2}{S,3}{a,4}, 3,3)

6. (babb±_K, {±„,0}{S,l}{a,2}{S,3}{a,4}{S,6}, 3,3,3)

7. (abbl_K, {l_H,0}{S,l}{a,2}{S,3}{a,4}{S,6}{b,7}, 3,3,3)

8. (abbl_K, {l_H,0}{S,l}{a,2}{S,3}, 3,3,3,2)

9. (bbl_K> {±_H,0}{S,l}{a,2}{S,3}{a,4}, 3,3,3,2)

10. (bb±_K, {l_H,0}{S,l}{a,2}{S,3}{a,4}{S,6}₎ 3,3,3,2,3)

11. (bl_K, {l_H,0}{S,l}{a,2}{S,3}{a,4}{S,6}{b,7}, 3,3,3,2,3)

12. (bl_K, {±_H,0}{S,l}{a,2}{S,3}, 3,3,3,2,3,2)

13. (1_K, {±_1I,0}{S,l}{a_>2}{S,3}{b,5}, 3,3,3,2,3,2)

14. (1_K, {1_H,0}{S,1}, 3,3,3,2,3,2,2)

15. (1_K, {1_H,0}{S',*}, 3,3,3,2,3,2,2,1) — разбор завершен.

Соответствующая цепочка вывода будет иметь вид (используется правосторон­ний вывод): S' => S => SaSb => SaSaSbb => SaSabb => SaSaSbabb => SaSababb => Saababb => aababb.

Невозможно непосредственно сравнить работу двух рассмотренных вариантов распознавателей: восходящего (LR) и нисходящего (LL). Это очевидно, посколь­ку приведенная в примере грамматика не является ЬЦ1)-грамматикой. Соответ­ственно, она не может быть разобрана и методом рекурсивного спуска (можно убедиться в этом, построив множества FIRST и FOLLOW для символов грамма­тики: FIRST(1,S) = {a}, FOLLOW(l,S) = {а,ЬЛ}; FIRST(1,S) n FOLLOW(l.S) * 0). На основании этой грамматики вообще невозможно построить нисходящий рас­познаватель, поскольку она явно содержит левую рекурсию. Устранив левую рекур­сию (см. алгоритм в разделе «Преобразование КС-грамматик. Приведенные грам­матики», глава 11) и выполнив ряд несложных преобразований, можно получить эквивалентную ей грамматику G"({a,b},{S},{S->A|aSbS},S), которая будет относить­ся к классу LL(l)-rpaMMaraK (действительно, для нее FIRST(1,S) = {a}, FOLLOW(l,S) = = {ЬД};. FIRST(1,S) n FOLLOW(l,S) = 0)¹. Теперь уже возможно сравнить ра­боту двух вариантов распознавателей — нисходящего и восходящего.

Чтобы доказать, что две рассмотренные грамматики эквивалентны (определяют один и тот же язык: L(G) = L(G")), предлагаем читателям выполнить преобразования G в G" са­мостоятельно. Это несложно: первым шагом будет устранение левой рекурсии, затем не­обходимо несколько раз выполнить левую факторизацию (см. раздел «Нисходящие распознаватели КС-языков без возвратов» этой главы), после чего дальнейшее преобра­зование становится очевидным.

Несмотря на то что распознаватель на основе LL(l)-rpaMMaTHKH и в данном слу­чае имеет более простой алгоритм функционирования, нельзя сказать, что им легче воспользоваться, поскольку его создание требует дополнительных преоб­разований исходной грамматики. Для более сложных LR(l)-rpaMMaTHK такие преобразования могут быть в принципе невозможны, поскольку класс языков, заданных LR(l)-rpaMMaTHKaMH, шире, чем класс языков, заданных LL(l)-rpaM-матиками. Поэтому для конкретной заданной грамматики чаще бывает проще построить восходящий распознаватель, чем нисходящий.

На практике LR(k)-rpaMMaTHKH при к > 1 не применяются. На это имеются две причины. Во-первых, управляющая таблица для LR(k)-rpaMMaraKH при к > 1 бу­дет содержать очень большое число состояний, и распознаватель будет достаточ­но сложным и не столь эффективным¹. Во-вторых, для любого языка, определяе­мого LR(k)-грамматикой, существует LR(l)-rpaMMaraKa, определяющая тот же язык. То есть для любой LR(k)-rpaMMaraKH с к > 1 всегда существует эквива­лентная ей LR(l)-rpaMMaTHKa. Более того, для любого детерминированного КС-языка существует LR(l)-rpaMMaraKa (другое дело, что далеко не всегда такую грамматику можно легко построить)².

Грамматики предшествования (основные принципы)

Еще одним распространенным классом КС-грамматик, для которых возмож­но построить восходящий распознаватель без возвратов, являются грамматики предшествования. Так же как и распознаватель рассмотренных выше LR-грам-матик, распознаватель для грамматик предшествования строится на основе алго­ритма «сдвиг-свертка» («перенос-свертка»), который в общем виде был рассмот­рен в разделе «Распознаватели КС-языков с возвратом», глава 11. Принцип организации распознавателя входных цепочек языка, заданного грам­матикой предшествования, основывается на том, что для каждой упорядоченной пары символов в грамматике устанавливается некоторое отношение, называемое отношением предшествования. В процессе разбора входной цепочки расширен­ный МП-автомат сравнивает текущий символ входной цепочки с одним из сим­волов, находящихся на верхушке стека автомата. В процессе сравнения проверя­ется, какое из возможных отношений предшествования существует между этими двумя символами. В зависимости от найденного отношения выполняется либо

¹ Безусловно, при любых значениях к распознаватель для LR(k)-грамматик остается ли­ нейным распознавателем — необходимые вычислительные ресурсы для него линейно за­ висят от длины входной цепочки символов. Но с ростом к будет расти и коэффициент зависимости. Из алгоритма функционирования распознавателя видно, что этот коэффи­ циент напрямую связан с объемом управляющей таблицы, причем ее объем возрастает в квадратичной зависимости от величины к.

² Число состояний управляющей таблицы для практически интересных LR(l)-rpaMMaTHK также весьма велико. А к классу 1Л(0)-грамматик такие грамматики почти никогда не относятся. На практике чаще всего используются промежуточные между LR(0) и LR(l) методы, известные под названиями SLR(l) — Simple («Простые») LR(1) — и LALR(l) — Look Ahead («С заглядыванием вперед») LR(1) [6, 12, 23].

сдвиг (перенос), либо свертка. При отсутствии отношения предшествования ме­жду символами алгоритм сигнализирует об ошибке.

Задача заключается в том, чтобы иметь возможность непротиворечивым образом определить отношения предшествования между символами грамматики. Если это возможно, то грамматика может быть отнесена к одному из классов грамматик предшествования.

Существует несколько видов грамматик предшествования. Они различаются по тому, какие отношения предшествования в них определены и между какими ти­пами символов (терминальными или нетерминальными) могут быть установле­ны эти отношения. Кроме того, возможны незначительные модификации функ­ционирования самого алгоритма «сдвиг-свертка» в распознавателях для таких грамматик (в основном на этапе выбора правила для выполнения свертки, когда возможны неоднозначности) [5, 6, 23, 65].

Выделяют следующие виды грамматик предшествования:

• простого предшествования;

• расширенного предшествования;

• слабого предшествования;

• смешанной стратегии предшествования;

• операторного предшествования.

Далее будут рассмотрены два наиболее простых и распространенных типа — грамматики простого и операторного предшествования.

Грамматики простого предшествования

Грамматикой простого предшествования называют такую приведенную КС-грам­матику¹ G(VN,VT,P,S), V = VTuVN, в которой:

1. Для каждой упорядоченной пары терминальных и нетерминальных символов выполняется не более чем одно из трех отношений предшествования:

О Bj =• Bj (V Bj,BjeV), если и только если 3 правило А->хВ₍В;у еР, где AeVN,

О Bj <• Bj (V Bj,BjeV), если и только если 3 правило A-»xBjDy еР и вывод D=>*S_jZ, где A,DeVN, x,y,zeV*;

О Bj'•> Bj (V Bj,BjeV) , если и только если 3 правило A-»xCBjy еР и вывод C=>*zB_; или 3 правило A->xCDy еР и выводы C=>*zBj и D=>*Bj\v, где A,C,DeVN, x,y,z,weV*.

2. Различные правила в грамматике имеют разные правые части (то есть в грам­ матике не должно быть двух различных правил с одной и той же правой ча­ стью).

Напоминаем, что КС-грамматика называется приведенной, если она не содержит циклов, бесплодных и недостижимых символов и А.-правил (см. раздел «Преобразование КС-грамматик. Приведенные грамматики», глава 11).

Отношения =•, <• и •> называют отношениями предшествования для символов. Отношение предшествования единственно для каждой упорядоченной пары символов. При этом между какими-либо двумя символами может и не быть от­ношения предшествования — это значит, что они не могут находиться рядом ни в одном элементе разбора синтаксически правильной цепочки. Отношения пред­шествования зависят от порядка, в котором стоят символы, и в этом смысле их нельзя путать со знаками математических операций — они не обладают ни свой­ством коммутативности, ни свойством ассоциативности. Например, если извест­но, что В₍ •> Bj, то не обязательно выполняется Bj <• В; (поэтому знаки предшест­вования иногда помечают специальной точкой: =•, <•, •>). Для грамматик простого предшествования известны следующие полезные свой­ства:

• всякая грамматика простого предшествования является однозначной;

• легко проверить, является или нет произвольная КС-грамматика граммати­кой простого предшествования (для этого достаточно проверить рассмотрен­ные выше свойства грамматик простого предшествования или воспользовать­ся алгоритмом построения матрицы предшествования, который рассмотрен далее).

Как и для многих других классов грамматик, для грамматик простого предшест­вования не существует алгоритма, который бы мог преобразовать произвольную КС-грамматику в грамматику простого предшествования (или доказать, что пре­образование невозможно).

Метод предшествования основан на том факте, что отношения предшествования между двумя соседними символами распознаваемой строки соответствуют трем следующим вариантам:

• Bj <■ B_i+1, если символ B_i+1 — крайний левый символ некоторой основы (это отношение между символами можно назвать «предшествует основе» или про­сто «предшествует»);

• Bj •> B_i+1, если символ Bj — крайний правый символ некоторой основы (это отношение между символами можно назвать «следует за основой» или просто «следует»);

• Bj =• B_i+1, если символы В_; и B_i+i принадлежат одной основе (это отношение между символами можно назвать «составляют основу»).

Исходя из этих соотношений, выполняется разбор строки для грамматики пред­шествования.

Суть принципа такого разбора можно пояснить на рис. 12.5. На нем изображена входная цепочка символов ау(38 в тот момент, когда выполняется свертка цепоч­ки у. Символ а является последним символом подцепочки а, а символ Ъ — первым символом подцепочки р\ Тогда, если в грамматике удастся установить непроти­воречивые отношения предшествования, то в процессе выполнения разбора по алгоритму «сдвиг-свертка» можно всегда выполнять сдвиг до тех пор, пока меж­ду символом на верхушке стека и текущим символом входной цепочки сущест­вует отношение <■ или =•. А как только между этими символами будет обнару-

жено отношение •>, так сразу надо выполнять свертку. Причем для выполнения свертки из стека надо выбирать все символы, связанные отношением =•. То, что все различные правила в грамматике предшествования имеют различные правые части, гарантирует непротиворечивость выбора правила при выполнении свертки.

Таким образом, установление непротиворечивых отношений предшествования между символами грамматики в комплексе с несовпадающими правыми частями различных правил дает ответы на все вопросы, которые надо решить для органи­зации работы алгоритма «сдвиг-свертка» без возвратов.

а

a

Y

Ь

Р

6

<. =. .>

Рис. 12.5. Отношения между символами входной цепочки в грамматике предшествования

На основании отношений предшествования строят матрицу предшествования грамматики. Строки матрицы предшествования помечаются первыми (левыми) символами, столбцы — вторыми (правыми) символами отношений предшество­вания. В клетки матрицы на пересечении соответствующих столбца и строки по­мещаются знаки отношений. При этом пустые клетки матрицы говорят о том, что между данными символами нет ни одного отношения предшествования. Матрицу предшествования грамматики сложно построить, опираясь непосредст­венно на определения отношений предшествования. Удобнее воспользоваться двумя дополнительными множествами — множеством крайних левых и множе­ством крайних правых символов относительно нетерминальных символов грам­матики G(VN,VT,P,S), V = VTuVN. Эти множества определяются следующим образом:

• L(A) = {X | 3 A=>*Xz}, AeVN, XeV, zeV — множество крайних левых симво­лов относительно нетерминального символа А (цепочка z может быть и пус­той цепочкой);

• R(A) = {X | 3 A=>*zX}, AeVN, XeV, zeV* — множество крайних правых сим­волов относительно нетерминального символа А.

Иными словами, множество крайних левых символов относительно нетерми­нального символа А — это множество всех крайних левых символов в цепочках, которые могут быть выведены из символа А. Аналогично, множество крайних правых символов относительно нетерминального символа А — это множество всех крайних правых символов в цепочках, которые могут быть выведены из символа А.

Тогда отношения предшествования можно определить так:

• Bj =• Bj (V Bi,BjeV), если 3 правило А-^хВ^у е Р, где AeVN, x,yeV;

• Bj <• Bj (V B_i7BjeV), если 3 правило A-McBiDy e P и BjeL(D), где A,DeVN,

x,yeV*;

□ B, •> B, (V Bj.BjsV), если Э правило A-»xCBjy e P и BisR(C) или З правило A^xCDye P и B_:eR(C), BjsL(D), где A,C,DeVN, x,yeV*.

Такое определение отношений удобнее на практике, так как не требует построе­ния выводов, а множества L(A) и R(A) могут быть построены для каждого не­терминального символа AeVN грамматики G(VN,VT,P,S), V = VTuVN по очень простому алгоритму.

Шаг 1. V AeVN:

Ro(A) = {X | А^уХ, XeV, yeV*}, L₀(A) = {X | A-+Xy, XeV, yeV*}, i := 1. Для каждого нетерминального символа А ищем все правила, содержащие А в ле­вой части. Во множество L(A) включаем самый левый символ из правой части правил, а во множество R(A) — самый крайний правый символ из правой части. Переходим к шагу 2. Шаг 2. V AeVN:

Ri (A) = R,!(A) ц R_M(B), V В е (Л_И(А) n VN), Ц (А) = Lh(A) и L_i4(B), V В е (L_M(A) n VN). Для каждого нетерминального символа А: если множество L(A) содержит нетер­минальные символы грамматики А', А", ..., то его надо дополнить символами, входящими в соответствующие множества L(A'), L(A"), ... и не входящими в L(A). Ту же операцию надо выполнить для R(A).

Шаг 3. Если 3 AeVN: Ri(A) * Ri_i(A) или Lj(A) * Ь_И(А), то i:=i+l и вернуться к шагу 2, иначе построение закончено: R(A) = Rj(A) и L(A) = Lj(A). Если на предыдущем шаге хотя бы одно множество L(A) или R(A) для неко­торого символа грамматики изменилось, то надо вернуться к шагу 2, иначе по­строение закончено.

После построения множеств L(A) и R(A) по правилам грамматики создается матрица предшествования. Матрицу предшествования дополняют символами 1_и и ±_к (начало и конец цепочки). Для них определены следующие отношения предшествования:

±_н <■ X, V aeV, если 3 S=>*Xy, где SeVN, yeV или (с другой стороны) если

XeL(S);

1_К •> X, V aeV, если 3 S=>*yX, где SeVN, yeV* или (с другой стороны) если

XeR(S). Здесь S — целевой символ грамматики.

Матрица предшествования служит основой для работы распознавателя языка, заданного грамматикой простого предшествования.

Алгоритм «сдвиг-свертка» для грамматики простого предшествования

Данный алгоритм выполняется расширенным МП-автоматом с одним состояни­ем. Отношения предшествования служат для того, чтобы определить в процессе выполнения алгоритма, какое действие — сдвиг или свертка — должно выпол­няться на каждом шаге алгоритма, и однозначно выбрать цепочку для свертки. Однозначный выбор правила при свертке обеспечивается за счет различия пра­вых частей всех правил грамматики. В начальном состоянии автомата считываю-

щая головка обозревает первый символ входной цепочки, в стеке МП-автомата находится символ ±_н (начало цепочки), в конец цепочки помещен символ _L_K (ко­нец цепочки). Символы _1__н и J__K введены для удобства работы алгоритма, в язык, заданный исходной грамматикой, они не входят.

Разбор считается законченным (алгоритм завершается), если считывающая го­ловка автомата обозревает символ _L_K и при этом больше не может быть выполне­на свертка. Решение о принятии цепочки зависит от содержимого стека. Автомат принимает цепочку, если в результате завершения алгоритма в стеке находятся начальный символ грамматики S и символ 1_н. Выполнение алгоритма может быть прервано, если на одном из его шагов возникнет ошибка. Тогда входная це­почка не принимается.

Алгоритм состоит из следующих шагов.

Шаг 1. Поместить в верхушку стека символ 1,„ считывающую головку — в нача­ло входной цепочки символов.

Шаг 2. Сравнить с помощью отношения предшествования символ, находящийся на вершине стека (левый символ отношения), с текущим символом входной це­почки, обозреваемым считывающей головкой (правый символ отношения).

Шаг 3. Если имеет место отношение <• или =•, то произвести сдвиг (перенос теку­щего символа из входной цепочки в стек и сдвиг считывающей головки на один шаг вправо) и вернуться к шагу 2. Иначе перейти к шагу 4.

Шаг 4. Если имеет место отношение •>, то произвести свертку. Для этого надо найти на вершине стека все символы, связанные отношением =• («основу»), уда­лить эти символы из стека. Затем выбрать из грамматики правило, имеющее правую часть, совпадающую с основой, и поместить в стек левую часть выбран­ного правила (если символов, связанных отношением =-<$]command>, на вер­хушке стека нет, то в качестве основы используется один, самый верхний символ стека). Если правило, совпадающее с основой, найти не удалось, то необходимо прервать выполнение алгоритма и сообщить об ошибке, иначе, если разбор не за­кончен, то вернуться к шагу 2.

Шаг 5. Если не установлено ни одно отношение предшествования между теку­щим символом входной цепочки и символом на верхушке стека, то надо пре­рвать выполнение алгоритма и сообщить об ошибке.

Ошибка в процессе выполнения алгоритма возникает, когда невозможно выпол­нить очередной шаг — например, если не установлено отношение предшествова­ния между двумя сравниваемыми символами (на шагах 2 и 4) или если не удается найти нужное правило в грамматике (на шаге 4). Тогда выполнение алгоритма немедленно прерывается.

Пример распознавателя для грамматики простого предшествования

Рассмотрим в качестве примера грамматику G({+,-,/,*,a,b}, {S,R,T,F,E}, P, S) с правилами:

Р:

S -> TR | Т

R _> ₊т | -Т | +TR | -TR

Т -> EF | Е

F -> *Е | /Е | *EF | /EF

Е -+ (S) | а | b Эта нелеворекурсивная грамматика для арифметических выражений над симво­лами а и b уже несколько раз использовалась в качестве примера для построения распознавателей (см. раздел «Распознаватели КС-языков с возвратом», глава И). Хотя эта грамматика и содержит цепные правила, легко увидеть, что она не со­держит циклов, совпадающих правых частей правил и ^-правил, следовательно, по формальным признакам ее можно отнести к грамматикам простого предшест­вования. Осталось определить отношения предшествования. Построим множества крайних левых и крайних правых символов относительно нетерминальных символов грамматики.

1. Шаг 1.

L₀(S) = {Т} Ro(S) - {R, Т}

L₀(R) = {+, -} R₀(R) " {R Т}

Lo(T) - {Е} Ro(T) - {Е, F}

L₀(F) -{*,/} R₀(F) = {E,F}

' Lo(E) - {(, a, b} R₀(E) = {), a, b}

2. Шаг 2.

Li(S)-{T;E) R,(S) - {R, T E, F}

L,(R) = {+, -} Ri(R) = {R T, E, F}

L,(T) = {E, (, a, b} Ri(I) r {E, F, ), a, b}

L,(F) = {*, /} Rj(F) = {E, F, ), a, b }

L_t(E) = {(, a, b} R,(E) = {), a, b}

3. Шаг 3. Имеется L₀(S) * L,(S), возвращаемся к шагу 2.

4. Шаг 2.

L₂(S) = {Т, Е, (, a, b} R₂(S) = {R, T, E, F, ), а, Ь}

L₂(R) = {+, -} R₂(R) = {R t ^E> ^F>)- ^a' ^b>

L₂(T) = {E, (, a, b} R₂(T.) = {E, F, ), a, b} L₂(F) = {*, /} R₂(F) = (E, F, ), a, b }

L₂(E) = {(, a, b} R₂(E) - {), a, b}

5. Шаг З. Имеется L_t(S) Ф L₂(S), возвращаемся к шагу 2.

6. Шаг 2.

L₃(S) = {Т, Е, (, a, b} R₃(S) - {R, T E, F, ), а, Ь}

L₃(R) - {+, -} R₃(R) " {R. T, E, F, ), а, Ь}

L₃(T) - {Е, (, a, b} R₃(T) - {Е, F, ), а, Ь}

L₃(F) - {*, /} R₃(F) - {Е, F, ), a, b }

L₃(E) = {(, a, b} R₃(E) = {), a, b}

7. Шаг 3. Ни одно множество не изменилось, построение закончено. Результат: L(S) - {Т, Е, (, a, b} R(S) - {R, T, E, F, ), а, Ь} L(R) - {+, -} R(R) - {R, T, E, F, ), а, Ь}

R(T) = {Е, F, ), а, Ь}

R(F) т {E, F, ), а, Ь }

R(E) = {), а, Ь}

На основании построенных множеств крайних левых и крайних правых симво­лов и правил грамматики построим матрицу предшествования. Результат приве­ден в табл. 12.4.

Таблица 12.4. Таблица предшествования для грамматики простого предшествования

+

-

*

/

(

)

а

b

S

R

Т

F

Е

К

+

<■

<•

<•

=■

<•

-

<•

<•

<•

=■

<■

*

<•

<•

<•

=■

/

<•

<•

<•

-•

(

<■

<•

<•

=•

<•

<■

)

•>

>

•>

•>

•>

>

■ >

■>

а

•>

•>

•>

■>

■>

•>

•>

■>

b

>

•>

•>

•>

'>

• >

>

■>

S

«•

R

•>

■>

Т

<•

<■

•>

=.

■>

F

•>

•>

•>

•>

■>

Е

•>

■>

<•

<•

•>

•>

=■

■>

К

<•

<•

<

<■

<•

Поясним построение таблицы на примере символа +.

Во-первых, в правилах грамматики R -» +Т | +TR символ + стоит слева от симво­ла Т. Значит, в строке символа + в столбце, соответствующем символу Т, ставим знак =•. Кроме того, во множество ЦТ) входят символы Е, (, а, Ь. Тогда в строке символа + во всех столбцах, соответствующих этим четырем символам, ставим знак <•.

Во-вторых, символ + входит во множество L(R), а в грамматике имеются прави­ла вида S -> TR и R -» +TR | -TR. Следовательно, надо рассмотреть также мно- жество R(T). Туда входят символы Е, F, ), а, Ь. Значит, в столбце символа + во всех строках, соответствующих этим пяти символам, ставим знак •>. Больше символ + ни в какие множества не входит и ни в каких правилах не встречается. Продолжая эти рассуждения для остальных терминальных и нетерминальных символов грамматики, заполняем все ячейки матрицы предшествования, приве­денной выше. Если окажется, что согласно логике рассуждений в какую-либо клетку матрицы предшествования необходимо поместить более чем один-един­ственный знак =•, <• или •>, то это означает, что исходная грамматика не являет­ся грамматикой простого предшествования.

Отдельно можно рассмотреть заполнение строки для символа 1_и (начало стро­ки) и столбца для символа ±_к (конец строки). Множество L(S), где S - целевой символ, содержит символы Т, Е, (, а, Ь. Помещаем знак <• в строку, соответствую­щую символу 1„ для всех пяти столбцов, соответствующих этим символам. Ана­логично, множество R(S) содержит символы R, T, E, F, ), а, Ь. Помещаем знак •> в столбец, соответствующий символу 1_к для всех семи строк, соответствующих этим символам.

Рассмотрим работу алгоритма распознавания на примерах. Последовательность разбора будем записывать в виде последовательности конфигураций МП-авто­мата из трех составляющих:

• не просмотренная автоматом часть входной цепочки;

• содержимое стека;

• последовательность примененных правил грамматики.

Так как автомат имеет только одно состояние, то для определения его конфигу­рации достаточно двух составляющих - положения считывающей головки во входной цепочке и содержимого стека. Последовательность номеров правил не­сет дополнительную полезную информацию, по которой можно построить це­почку или дерево вывода (кроме того, последовательность примененных правил делает пример более наглядным). Правила в грамматике нумеруются в направ­лении слева направо и сверху вниз (всего в грамматике имеется 15 правил). Будем обозначать такт автомата символом *•. Введем также дополнительное обо­значение *_п, если на данном такте выполнялся перенос, и -н_с, если выполнялась свертка.

Последовательности разбора цепочек входных символов будут, таким образом, иметь вид. Пример 1. Входная цепочка а+а*Ь.

1. {а+а*Ы_к; 1_Н; 0} +_п

2. {+а*Ь±_к; 1_на; 0} +_с

3. {+a*bl_K; _L_HE; 14} *_с

4. {+а*Ь±_к; 1_ИТ; 14,8}

5. {а*ЬХ_к; 1„Т+; 14,8}

6. {*Ы_К; ±_нТ+а; 14,8}

{*Ь±_К; ±„Т+Е; 14,8,14}

8. {Ь±_к; 1Д+Е*; 14,8,14} *_п

9. {1_к; ±_НТ+Е*Ь; 14,8,14} +_с

10. {1_к; 1_НТ+Е*Е; 14,8,14,15} *_с

11. {±_к; ±_HT+EF; 14,8,14,15,9}+_с

12. {1_к; 1_НТ+Т; 14,8,14,15,9,7} +_с

13. {±_к; 1_HTR; 14,8,14,15,9,7,3} +_с

14. {1_к; ±_HS; 14,8,14,15,9,7,3,1}, алгоритм завершен, цепочка принята.

Соответствующая цепочка вывода будет иметь вид (используется правосторон­ний вывод): S => TR => Т+Т => T+EF => Т+Е*Е => Т+Е*Ь => Т+а*Ь => Е+а*Ь => а+а*Ь.

Дерево вывода, соответствующее этой цепочке, приведено на рис. 12.6.

(?) £r\

© 0 )S)

_{© f/r}

(a) Q (e)

Рис. 12.6. Первый пример дерева вывода для грамматики простого предшествования

Пример 2. Входная цепочка (а+а)*Ь.

1. {(а+а)*Ь±_к; 1„; 0} +_п

2. {a+a)*b±_K; i_H(; 0} +„

3. {+а)*Ы_к; 1_и(а; 0} +_с

4. {+а)*Ы_к; 1_Н(Е; 14} +_с

5. {+а)*Ь±_к; 1_Н(Т; 14,8} +_п

6. {а)*Ь±_к; 1_Н(Т+; 14,8} *_п

7. {)*Ы_К; ±_н(Т+а; 14,8} +_с

8. {)*Ы_К; ±_Н(Т+Е; 14,8,14} +_с

9. {)*Ы_К; 1_Н(Т+Т; 14,8,14,8} _+с

10. {)*Ы_К; 1_H(TR; 14,8,14,8,3} +_с

11. {)*Ь±_К; ±_H(S; 14,8,14,8,3,1}+_п

12. {*Ъ±_к; ±_H(S); 14,8,14,8,3,1} +_с

13. {*Ы_К; ±_НЕ; 14,8,14,8,3,1,13} +_п

14. {Ь1_к; ±_НЕ*; 14,8,14,8,3,1,13} +_п

15. {1_к; 1_НЕ*Ь; 14,8,14,8,3,1,13} +_с

16. {±_к; 1_НЕ*Е; 14,8,14,8,3,1,13,15} +_с

17. {1_к; 1_HEF; 14,8,14,8,3,1,13,15,9} +_с

18. {1_к; 1_НТ; 14,8,14,8,3,1,13,15,9,7} _tc

19. {1_к; _L_HS; 14,8,14,8,3,1,13,15,9,7,2}, алгоритм завершен, цепочка принята.

Соответствующая цепочка вывода будет иметь вид (используется правосторон­ний вывод): S => Т => EF => Е*Е => E*b => (S)*b =^> (TR)*b => (T+T)*b => (T+E)*b => (T+a)*b => (E+_a)*b => (a+a)*b. Дерево вывода, соответствующее этой цепочке, приведено на рис. 12.7.

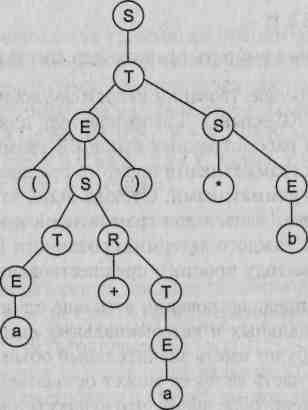
Рис. 12.7. Второй пример дерева вывода для грамматики простого предшествования

Пример 3. Входная цепочка а+а*.

1. {а+а*±_к; 1_И; 0} +_п

2. {+а*±_к; 1„а; 0} +_с

3. {+а*1_к; 1_ПЕ; 14} +_с

4. {+а*±_к; ±_НТ; 14,8} +_п

5. {а*±_к; ХД+; 14,8} +_п

6. {*1_к; ±_нТ+а; 14,8} +_е

7. {*±_к; 1„Т+Е; 14,8,14} +_п

8. {±_к; ±_ИТ+Е*; 14,8,14} +

9. Ошибка! (Нет отношений предшествования между символами * и _L_K.)

Пример 4. Входная цепочка а+а)*Ь.

1. {а+а)*Ы_к; 1_и; 0} _+п

2. {+а)*Ы_к; 1_на; 0} _%

3. {+а)*Ь±_к; Х,Е; 14} +_с

4. {+а)*Ы_к; 1„Т; 14,8} *_п

5. {а)*Ь±_к; ±_НТ+; 14,8} +_п

6. {)*Ы_К; 1_кТ+а; 14,8} +_с

7. {)*Ы_К; ±_НТ+Е; 14,8,14} +_с

8. {)*Ы_К; 1_НТ+Т; 14,8,14,8} ^_с

9. {)*Ы_К; 1_HTR; 14,8,14,8,3} _+с

10. {)*bl_K; 1„S; 14,8,14,8,3,1} ^_п

11. {*Ы_К; 1_HS); 14,8,14,8,3,1} +_с

12. Ошибка! (Невозможно выбрать правило для свертки на этом шаге.)

Грамматики простого предшествования являются удобным механизмом для ана­лиза входных цепочек КС-языков. Распознаватель для этого класса грамматик строить легче, чем для рассмотренных выше LR-грамматик. Однако при этом класс языков, заданных грамматиками простого предшествования уже, чем класс языков, заданных LR-грамматиками. Отсюда ясно, что не всякий детермини­рованный КС-язык может быть задан грамматикой простого предшествования, а следовательно, не для каждого детерминированного КС-языка можно постро­ить распознаватель по методу простого предшествования.

У грамматик простого предшествования есть еще один недостаток — при боль­шом количестве терминальных и нетерминальных символов в грамматике мат­рица предшествования будет иметь значительный объем (при этом следует заме­тить, что значительная часть ее ячеек может оставаться пустой). Поиск в такой матрице может занять некоторое время, что существенно при работе распознава­теля — фактически время поиска линейно зависит от числа символов в грамматике, а объем матрицы — квадратично. Для того чтобы избежать хранения и обработки таких матриц, можно выполнить «линеаризацию матрицы предшествования». Тогда каждый раз, чтобы установить отношение предшествования между двумя символами, будет выполняться не поиск по матрице, а вычисление некой специ­ально организованной функции. Вопросы линеаризации матрицы предшествова­ния здесь не рассматриваются, с применяемыми при этом методами можно озна­комиться в [5, 6, т. 2, 23, 32].

Грамматики операторного предшествования

Операторной грамматикой называется КС-грамматика без Х-правил, в которой правые части всех правил не содержат смежных нетерминальных символов. Для операторной грамматики отношения предшествования можно задать на множе­стве терминальных символов (включая символы J_„ и J__K).

Грамматикой операторного предшествования называется операторная КС-грам­матика G(VN,VT,P,S), V = VTuVN, для которой выполняются следующие усло­вия:

1. Для каждой упорядоченной пары терминальных символов выполняется не более чем одно из трех отношений предшествования:

О а =• Ь, если и только если существует правило A-»xaby еР или правило А-wcaCby, где a,beVT, A.CeVN, x.yeV;

О а <■ b, если и только если существует правило А->хаСу еР и вывод C=>*bz или вывод C=>*Dbz, где a,beVT, A,C,DeVN, x,y,zeV";

О а •> b, если и только если существует правило А-»хСЬу еР и вывод C=>*za или вывод C=>*zaD, где a,beVT, A,C,DeVN, x.y.zeV*¹.

2. Различные порождающие правила имеют разные правые части, ^.-правила от­ сутствуют.

Отношения предшествования для грамматик операторного предшествования определены таким образом, что для них выполняется еще одна особенность — правила грамматики операторного предшествования не могут содержать двух смежных нетерминальных символов в правой части. То есть в грамматике опера­торного предшествования G(VN,VT,P,S), V = VTuVN не может быть ни одного правила вида: А-»хВСу, где A,B,CeVN, x,yeV* (здесь х и у — это произвольные цепочки символов, могут быть и пустыми).

Для грамматик операторного предшествования также известны следующие свой­ства:

• всякая грамматика операторного предшествования задает детерминирован­ный КС-язык (но не всякая грамматика операторного предшествования при этом является однозначной!);

• легко проверить, является или нет произвольная КС-грамматика граммати­кой операторного предшествования (точно так же, как и для простого пред­шествования).

Как и для многих других классов грамматик, для грамматик операторного пред­шествования не существует алгоритма, который бы мог преобразовать произ­вольную КС-грамматику в грамматику операторного предшествования (или до­казать, что преобразование невозможно).

Принцип работы распознавателя для грамматики операторного предшествова­ния аналогичен грамматике простого предшествования, но отношения предшест­вования проверяются в процессе разбора только между терминальными симво­лами.

В литературе отношения операторного предшествования иногда обозначают другими символами, отличными от «<■», «•>» и «=■», чтобы не путать их с отношениями простого предшествования. Например, встречаются обозначения «<°», «°>» и «=°». В данном по­собии путаница исключена, поэтому будут использоваться одни и те же обозначения, хотя, по сути, отношения предшествования несколько различны.

Для грамматики данного вида на основе установленных отношений предшество­вания также строится матрица предшествования, но она содержит только терми­нальные символы грамматики.

Для построения этой матрицы удобно ввести множества крайних левых и край­них правых терминальных символов относительно нетерминального символа А - L^l(A) или R^l(A):

• L'(A) = {t | 3 A=>*tz или Э A=>*Ctz }, где teVT, A,CeVN, zeV;

• R'(A) = {t | 3 A=>*zt или 3 A=>*ztC }, где teVT, A.CeVN, zeV*.

Тогда определения отношений операторного предшествования будут выглядеть так:

□ а =■ Ь, если 3 правило A—»xaby еР или правило U-»xaCby, где a,beVT, A,CeVN,

x,yeV;

• а <• b, если 3 правило А-»хаСу еР и ЬеЬ'(С), где a,beVT, A,CeVN, x,yEV*;

• а •> b, если 3 правило A-»xCby еР и aeR^C), где a,beVT, A,CeVN, x.yeV*. В данных определениях цепочки символов x,y,z могут быть и пустыми цепочками. Для нахождения множеств L'(A) и R'(A) предварительно необходимо выпол­ нить построение множеств L(A) и R(A), как это было рассмотрено ранее. Далее для построения L^l(A) и R'(A) используется следующий алгоритм:

Шаг 1. V AeVN:

R^l₀(A) = {t | A->ytB или A->yt, teVT, BeVN, yeV},

V₀(A) = {t | A->Bty или A->ty, teVT, BeVN, yeV}.

Для каждого нетерминального символа А ищем все правила, содержащие А в ле­вой части. Во множество L(A) включаем самый левый терминальный символ из правой части правил, игнорируя нетерминальные символы, а во множество R(A) — самый крайний правый терминальный символ из правой части правил. Перехо-цим к шагу 2.

Шаг 2. V AeVN:

R^li(A) = RV,(A) u RV,(B), V В e (R(A) n VN),

Ц(А) = LVi(A) u LVi(B), V В e (L(A) n VN).

Цля каждого нетерминального символа А: если множество L(A) содержит нетер­ минальные символы грамматики А', А" то его надо дополнить символами,

зходящими в соответствующие множества Ь'(А'), L^l(A"), ... и не входящими в L^l(A). Ту же операцию надо выполнить для множеств R(A) и R^l(A). Шаг 3. Если Э AeVN: R'^A) ± RVi(A) или Ц(А) * LVi(A), то i:=i+l и вернуться с шагу 2, иначе построение закончено: R(A) = R^A) и L(A) = 1Д(А). 1сли на предыдущем шаге хотя бы одно множество L'(A) или R'(A) для неко­торого символа грамматики изменилось, то надо вернуться к шагу 2, иначе по-:троение закончено.

практического использования матрицу предшествования дополняют симво-гами -L,, и ±_к (начало и конец цепочки). Для них определены следующие отноше-1ия предшествования:

±_н <• а, V aeVT, если 3 S=>*ax или 3 S=>*Cax, где S,CeVN, xeV* или если

aeL^l(S);

1_К ■> а, V aeVT, если 3 S=>*xa или 3 S=>*xaC, где S,CeVN, xeV* или если

aeR⁴(S).

Здесь S — целевой символ грамматики.

Матрица предшествования служит основой для работы распознавателя языка, заданного грамматикой операторного предшествования. Поскольку она содержит только терминальные символы, то, следовательно, будет иметь меньший размер, чем аналогичная матрица для грамматики простого предшествования. Следует отметить, что напрямую сравнивать матрицы двух грамматик нельзя — не всякая грамматика простого предшествования является грамматикой операторного пред­шествования, и наоборот. Например, рассмотренная далее в примере грамматика операторного предшествования не является грамматикой простого предшество­вания (читатели могут это проверить самостоятельно). Однако если две грамма­тики эквивалентны и задают один и тот же язык, то их множества терминальных символов должны совпадать. Тогда можно утверждать, что размер матрицы для грамматики операторного предшествования всегда будет меньше, чем размер матрицы эквивалентной ей грамматики простого предшествования. Все, что было сказано выше о способах хранения матриц для грамматик просто­го предшествования, в равной степени относится также и к грамматикам опера­торного предшествования, с той только разницей, что объем хранимой матрицы будет меньше.

Алгоритм «сдвиг-свертка» для грамматики операторного предшествования

Этот алгоритм в целом похож на алгоритм для грамматик простого предшество­вания, рассмотренный выше. Он также выполняется расширенным МП-автома­том и имеет те же условия завершения и обнаружения ошибок. Основное отличие состоит в том, что при определении отношения предшествования этот алгоритм не принимает во внимание находящиеся в стеке нетерминальные символы и при сравнении ищет ближайший к верхушке стека терминальный символ. Однако после выполнения сравнения и определения границ основы при поиске правила в грамматике нетерминальные символы следует, безусловно, принимать во вни­мание.

Алгоритм состоит из следующих шагов.

Шаг 1. Поместить в верхушку стека символ 1„, считывающую головку — в нача­ло входной цепочки символов.

Шаг 2. Сравнить с помощью отношения предшествования терминальный сим­вол, ближайший к вершине стека (левый символ отношения), с текущим симво­лом входной цепочки, обозреваемым считывающей головкой (правый символ отношения). При этом из стека надо выбрать самый верхний терминальный сим­вол, игнорируя все возможные нетерминальные символы. Шаг 3. Если имеет место отношение <■ или =•, то произвести сдвиг (перенос теку­щего символа из входной цепочки в стек и сдвиг считывающей головки на один шаг вправо) и вернуться к шагу 2. Иначе перейти к шагу 4.

Шаг 4. Если имеет место отношение •>, то произвести свертку. Для этого надо найти на вершине стека все терминальные символы, связанные отношением =■ («основу»), а также все соседствующие с ними нетерминальные символы (при определении отношения нетерминальные символы игнорируются). Если терми­нальных символов, связанных отношением =•, на верхушке стека нет, то в качест­ве основы используется один, самый верхний в стеке терминальный символ сте­ка. Все (и терминальные, и нетерминальные) символы, составляющие основу, надо удалить из стека, а затем выбрать из грамматики правило, имеющее правую часть, совпадающую с основой, и поместить в стек левую часть выбранного пра­вила. Если правило, совпадающее с основой, найти не удалось, то необходимо прервать выполнение алгоритма и сообщить об ошибке, иначе, если разбор не за­кончен, то вернуться к шагу 2.

Шаг 5. Если не установлено ни одно отношение предшествования между теку­щим символом входной цепочки и самым верхним терминальным символом в стеке, то надо прервать выполнение алгоритма и сообщить об ошибке.

Конечная конфигурация данного МП-автомата совпадает с конфигурацией при распознавании цепочек грамматик простого предшествования.

Пример построения распознавателя

для грамматики операторного предшествования

Рассмотрим в качестве примера грамматику для арифметических выражений над символами а и b G({+,-,/,*,a,b}, {S,T,E}, P, S):

Р:

S -*■ S+T I S-T i T

T -> T*E | T/E | E ■

E -> (S) | a | b

Эта грамматика уже много раз использовалась в качестве примера для построе­ния распознавателей.

Видно, что эта грамматика является грамматикой операторного предшествова­ния.

Построим множества крайних левых и крайних правых символов L(A), R(A) от­носительно всех нетерминальных символов грамматики. Рассмотрим работу ал­горитма построения этих множеств по шагам.

1. Шаг 1.

Lq(S) - {S, T}, Lo(T) = {Т, Е}, Lo(E) - {(, а, Ь}, 2. Шаг 2.

L,(S) - {S, Т, Е}_;

Ro(S) - {Т}, Ro(T) - {Е}, Ro(E) = {), a, b}, i - 1.

R_t(S) = {T, E},

Lt(T) = {T, E, (, a, b}, R,(T) - {E, ), a, b},

L,(E)-{С *.*>}. Ri(E) = {), a, b}.

|з. Шаг 3. Так как L₀(S) ф Lt(S), то i - 2 и возвращаемся к шагу 2.

И. Шаг 2.

L₂(S) - {S, Т, Е, (, a, b}, R₂(S) - {Т, Е, ), а, Ь}, L₂(T) - {Т, Е, (, а, Ъ}, R₂(T) - {Е, ), а, Ъ}, L₂(E) = {(, a, b}, R₂(E) = {), а, Ь}.

I 5. Шаг 3. Так как L^S) ф L₂(S), to i - 3 и возвращаемся к шагу 2.

|6. Шаг 2.

L₃(S) - {S, Т, Е, (, a, b}, R₃(S) = {Т, Е,), а, Ь},

L₃(T) - {Т, Е, (, a, b}, R₃(T) - {Е,), а, Ь},

L₃(E) = {(, a, b}, R₃(E) - {), а, Ь}.

R(S) - {Т, Е, ), а, Ъ}, R(T) = {Е, ), а, Ь}, R(E) = {), а, Ь}.

7. Построение закончено. Получили результат:

L(S) = {S, Т, Е, (, а, Ь},

ЦТ) = {Т, Е, (, а, Ь},

ЦЕ) - {(, а, Ь},

На основе полученных множеств построим множества крайних левых и крайни: правых терминальных символов 1ДА), R'(A) относительно всех нетерминаль ных символов грамматики. Рассмотрим работу алгоритма построения этих мне жеств по шагам.

R^co(S) = {+, -},

R'oCT) = {*, /}-

1. Шаг 1. L'₀(S) - {+, -}, L'o(T) - {*, /}, Ь'„(Е) - {(, a, b},

2. Шаг 2.

LS(S) - {+, -, *, /, (, a, b},RS(S) - {+, -, *, /}, L',(T) = {*,/,(, a, b}, RS(T) = {*, /, ), a, b}, LS(E) - {(, a, b}, RS(E) - {), a, b}.

3. Шаг 3. Так как L^S) ф L^l,(S), то i - 2 и возвращаемся к шагу 2.

4. Шаг 2.

L'₂(S) = {+, -, *, /, (, a, b},R'₂(S) - {+, -, *, /,), a, b }, L'₂(T) - {*, /, (, a, b}, R^l₂(T) = {*, /, ), a, b}, L*₂(E) = {(, a, b}, R'₂(E) = {), a, b}.

5. Шаг 3. Так как RS(S) ф R'₂(S), to i - 3 и возвращаемся к шагу 2.

6. Шаг 2.

L'₃(S) = {+, -, *, /, (. a, bJ.R^S) = {+, -, *, /. )• a, b }, LS(T) - {*, /, (, a, b}, R^l₃(T) = {*, /, ), a, b}

Ь*з(Е) = {(, a, b}, R'₃(E) = {), a, b}. 7. Построение закончено.

Получили результат:

L^l(S) = {+, -, *, /, (, a, b}, R'(S) = {+, -, *, /, ), а, Ъ }, L'(T) -{•,/,(, a, b}, Rt(T) = {*,/,), а, Ь}, L'(E) - {(, a, b}, Rt(E) = {), а, Ь}.

На основе этих множеств и правил грамматики G построим матрицу предшест­вования грамматики (табл. 12.5).

Таблица 12.5. Матрица предшествования грамматики

Сим­волы	+	-	*		(		а	b
+	•>	•>	<•	<■	<•	•>	<•	<•	.>
-	•>	•>	<•	<■	<•	•>	<•	<■	.>
*	■>	•> ■	■>	■>	<•	■>	<■	<•	.>
/	•>	•>	■>	■ >	<•	■ >	<•	<•	.>
(	<.	<.	<■		<•	=•	<.	<.
)	■>	• >	■>	■ >		• >			.>
а	•>	•>	•>	■ >		• >			.>
b	.>	.>	.>	.>		.>			.>
-L-и	<•	<■	<•	<•	<•		<•	<•

Поясним, как заполняется матрица предшествования в таблице на примере сим­вола +. В правиле грамматики S-»S+T (правило 1) этот символ стоит слева от не­терминального символа Т. Во множество L'(T) входят символы: *,/,(, а, Ь. Ста­вим знак <• в клетках матрицы, соответствующих этим символам, в строке для символа +. В то же время в этом же правиле символ + стоит справа от нетерми­нального символа S. Во множество R'(S) входят символы: +, -, *, /,), а, Ь. Ставим знак •> в клетках матрицы, соответствующим этим символам, в столбце для сим­вола +. Больше символ + ни в каком правиле не встречается, значит, заполнение матрицы для него закончено, берем следующий символ и продолжаем заполнять матрицу таким же методом, пока не переберем все терминальные символы.

Отдельно рассмотрим символы 1_И и ±_к. В строке символа Х_н ставим знак <• в клетках символов, входящих во множество L'(S). Это символы +, -, *, /, (, а, Ь. В столбце символа _1__к ставим знак •> в клетках символов, входящих во множест­во R'(S). Это символы +, -, *,/,), а, Ь.

Еще можно отметить, что в клетке соответствующей открывающей скобки (сим­вол () слева и закрывающей скобке (символ )) справа помещается знак =• («со­ставляют основу»). Так происходит, поскольку в грамматике присутствует пра­вило E->(S), где эти символы стоят рядом (через нетерминальный символ) в его правой части. Следует отметить, что понятия «справа» и «слева» здесь имен важное значение: в клетке соответствующей закрывающей скобке (символ ) слева и открывающей скобке (символ () справа знак отсутствует — такое сочет; ние символов недопустимо (отношение (=•) верно, а отношение )=•( — неверно

Алгоритм разбора цепочек грамматики операторного предшествования игнор] рует нетерминальные символы. Поэтому имеет смысл преобразовать исходну грамматику таким образом, чтобы оставить в ней только один нетерминальнь: символ. Тогда получим следующий вид правил:

S -» S+S | S-S | S (правила 1, 2 и 3) S -> S*S | S/S | S (правила 4, 5 и 6) S -» (S) | а | b (правила 7, 8 и 9)

Если теперь исключить бессмысленные правила вида S-»S, то получим следу! щее множество правил (нумерацию правил сохраним в соответствии с исходш грамматикой):

Р:

S —> S-t-S ] S-S (правила 1, 2)

S -> S*S | S/S (правила 4. 5)

S —> CS) 1 a I b (правила 7. 8 и 9)

Такое преобразование не ведет к созданию эквивалентной грамматики и выпо няется только для упрощения работы алгоритма (который при выборе прав] все равно игнорирует нетерминальные символы) после построения матриг предшествования. Полученная в результате преобразования грамматика не я ляется однозначной, но в алгоритм распознавания уже были заложены все нес ходимые данные о порядке применения правил при создании матрицы предц ствования, поэтому распознаватель остается детерминированным. Построенн таким способом грамматика называется «остовной» грамматикой. Вывод, uoj ченный при разборе на основе остовной грамматики, называют результатом «( товного» разбора или «остовным» выводом [6, 23, 32].

По результатам остовного разбора можно построить соответствующий ему в вод на основе правил исходной грамматики. Однако эта задача не представлю практического интереса, поскольку остовный вывод отличается от вывода на ( нове исходной грамматики только тем, что в нем отсутствуют шаги, связанн с применением цепных правил, и не учитываются типы нетерминальных chmi лов. Для компиляторов же распознавание цепочек входного языка заключав! не в нахождении того или иного вывода, а в выявлении основных синтакси¹ ских конструкций исходной программы с целью построения на их основе це1 чек языка результирующей программы. В этом смысле типы нетерминальн символов и цепные правила не несут никакой полезной информации, а нап] тив, только усложняют обработку цепочки вывода (или дерева вывода). Поэто для реального компилятора нахождение остовного вывода является даже 6oj полезным, чем нахождение вывода на основе исходной грамматики. Найденн остовный вывод в дальнейших преобразованиях уже не нуждается (более m робно см. главу «Основные принципы построения трансляторов»). Рассмотрим работу алгоритма распознавания на примерах. Последовательность разбора будем записывать в виде последовательности конфигураций расширен­ного МП-автомата из трех составляющих:

• не просмотренная автоматом часть входной цепочки;

• содержимое стека;

• последовательность примененных правил грамматики.

Так как автомат имеет только одно состояние, то для определения его конфигу­рации достаточно двух составляющих — положения считывающей головки во входной цепочке и содержимого стека. Последовательность номеров правил не­сет дополнительную полезную информацию, по которой можно построить це­почку или дерево вывода (кроме того, последовательность примененных правил делает пример более наглядным).

Будем обозначать такт автомата символом -г-. Введем также дополнительное обо­значение -5-_п, если на данном такте выполнялся перенос, и *_С) если выполнялась свертка.

Последовательности разбора цепочек входных символов будут, таким образом, иметь вид, приведенный ниже.

Пример 1. Входная цепочка а+а*Ь.

1. {а+а*Ы_к; 1_Н; 0} ^_п

2. {+а*Ы_к; 1„а; 0} +_с

3. {+а*Ы_к; 1_HS; 8} +_п

4. {а*Ы_к; 1_HS+; 8} +_п

5. {*b±_K; ±_HS+a; 8} +_с

6. {*Ы_К; ±_HS+S; 8,8} +_п •

7. {Ы_к; 1_HS+S*; 8,8} +_п

8. {1_К; 1_HS+S*b; 8,8} +_с

9. {1_К; 1_HS+S*S; 8,8,9} +_с

10. {1_К; 1_HS+S; 8,8,9,4} +_с

11. {1_К; ±_HS; 8,8,9,4,1} — разбор завершен, цепочка принята.

Соответствующая цепочка вывода будет иметь вид (используется правосторон­ний вывод): S => S+S => S+S*S => S+S*b => S+a*b => a+a*b.

Дерево вывода, соответствующее этой цепочке, приведено на рис. 12.8.

Следует отметить, что распознаватель, работающий на основе грамматики опера­торного предшествования, имеет еще одно весьма полезное свойство — за счет того, что при построении цепочки вывода не учитываются типы нетерминаль­ных символов, в результате игнорируются цепные правила, присутствующие в грамматике. Это сокращает длину цепочки вывода и размер дерева вывода¹.

¹ Из цепочки (и дерева) вывода удаляются цепные правила, которые, как будет показано да­лее, все равно не несут никакой полезной семантической (смысловой) нагрузки, а потому для компилятора являются бесполезными. Это положительное свойство распознавателя.

Рис. 12.8. Первый пример дерева вывода для грамматики операторного предшествования

Пример 2. Входная цепочка (а+а)*Ь.

1. {(а+а)*Ь±_к; ±_н; 0}+_п

2. {а+а)*Ы_к; 1„(; 0} -_п.

3. {+а)*Ь±_к; ±„(а; 0}+_с

4. {+а)*Ы_к; 1_H(S; 8} ^_п

5. {a)*bl_K; 1,,(S+; 8} +_п

6. {)*Ы_К; l_H(S+a; 8} +_с

7. {)*Ы_К; 1_H(S+S; 8,8} _+с

8. {)*bl_K; 1_H(S; 8,8,1} ^_п

9. {*Ы_К; 1_H(S); 8,8,1} +_с 10. {*Ы_К; 1_HS; 8,8,1,7} +_п И. {Ы_к; 1,,S*; 8,8,1,7} +_п

12. {1_К; l_HS*b; 8,8,1,7}.+_с ^ч '

13. {1_К; 1_HS*S; 8,8,1,7,9} +_с

14. {±_к; _L_HS; 8,8,1,7,9,4} — разбор завершен, цепочка принята.

Соответствующая цепочка вывода будет иметь вид (используется правосторс ний вывод): S => S*S => S*b => (S)*b => (S+S)*b => (S+a)*b => (a+a)*b. Дерево вывода, соответствующее этой цепочке, приведено на рис. 12.9.

Пример 3- Входная цепочка а+а*.

1. {а+а*1_к; 1_Н; 0} +_п 2.-{+а*-Ц;±_на;0}+_с

3. {+а*±_к; 1_HS; 8} ^_п

4. {a*l_K; 1_HS+; 8} ^_п

5. {*±_к; ±_HS+a; 8} +_с

6. {*1_К; 1..S+S; 8,8} ^_п

7. {1_К; X_HS+S*; 8,8} н-_с

8. Ошибка! (Нет правила для выполнения свертки на этом шаге.)

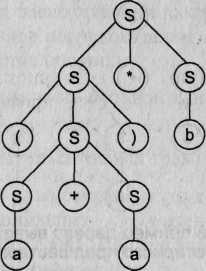
Рис. 12.9. Второй пример дерева вывода для грамматики операторного предшествования '

Пример 4. Входная цепочка а+а)*Ь.

1. {а+а)*Ь±_к; 1_Н; 0} +_п

2. {+а)*Ь±_к; ±_на; 0} +_с

3. {+a)*b±_K; 1_HS; 8} +_п

4. {a)*b; 1_HS+; 7} +_п

5. {)*Ы_К; l_HS+a; 8} +_с

6. {)*Ь±_К; 1_HS+S; 8,8} +_с

7. {)*Ь±_К; 1_HS; 8,8,1}

8. Ошибка! (Нет отношений предшествования между символами 1 . ч-н И ).)

Два первых примера наглядно демонстрируют, что приоритет onepai „

ленный в грамматике, влияет на последовательность разбора и следователь

ность применения правил, несмотря на то что нетерминальные сил распознователем не рассматриваются.

Как было сказано выше, матрица для грамматики операторного ni_u - „ редшествова-

ния всегда имеет меньший объем, чем матрица для эквивалентной е£

спознаватель 'аьные симво-меньше

:о терминаль-

простого предшествования (поскольку в первую из них входят тольк._г ные символы, а во вторую также и нетерминальные). Кроме того,

грамматики операторного предшествования игнорирует нетермина;

лы в процессе разбора, а значит, не учитывает цепные правила,

шагов и порождает более короткую цепочку вывода. Поэтому par

спознаватель для грамматик операторного предшествования всегда проще, чем, ^_о„ ^„ _u i распознаватель для эквивалентной ей грамматики простого предшествования.

Интересно, что поскольку распознаватель на основе грамматик с, „_,__„ „

операторного

предшествования не учитывает типы нетерминальных символов, то _ _{у л}..__ ^ он может ра~

оотать даже с некоторыми неоднозначными грамматиками, в котог

вила, различающиеся только типами нетерминальных символов. 1-г

кой грамматики может служить грамматика G"({a,b}, {S,A,B}, P, S) „ _ „„_.,„.

с правилами.

Р: S -

_jbiA ее 1 ь

А -» аАЬ | ab В -+ аВЬ | ab

Как и для любой другой грамматики операторного предшествования, расг ватель для этой грамматики будет детерминированным. Остовная грамм; построенная на ее основе, будет иметь только два правила вида: S—>aSb| ab. нозначность заключается в том, что каждому найденному остовному выво, дет соответствовать не один, а несколько выводов в исходной грамматике ( ном случае — всегда два вывода в зависимости от того, какое правило из ! будет применено на первом шаге вывода). Грамматики, содержащие пр; различающиеся только типами нетерминальных символов, практического: ния не имеют, а потому интереса для компиляторов не представляют.

К сожалению, хотя классы грамматик простого и операторного предшество несопоставимы¹, но класс языков операторного предшествования уже, чем языков простого предшествования. Поэтому не всегда возможно для язы: данного грамматикой простого предшествования, построить грамматику < торного предшествования. Соответственно, поскольку класс языков, зад; грамматиками операторного предшествования, еще более узок, чем даже языков, заданных грамматиками простого предшествования, то с помощы грамматик можно определить далеко не каждый детерминированный КС Грамматики операторного предшествования — это очень удобный инстр для построения распознавателей, но они имеют ограниченную область npi ния.

Соотношение классов КС-языков и КС-грамматик

В этом подразделе рассматриваются вопросы, связанные с отношениями различными классами известных КС-языков и КС-грамматик. Эти соотно представляются весьма интересными с точки зрения теории формальны ков. Многие из них совсем неочевидны. Однако читатель, интересующийся ко практическими аспектами построения трансляторов и компиляторов, в принципе пропустить этот подраздел.

Особенности восходящих

и нисходящих распознавателей

Выше были рассмотрены варианты двух основных типов распознавател цепочек КС-языков — восходящих и нисходящих. Далее можно не расе вать распознаватели с возвратом и табличные распознаватели, поскол практическое применение сильно ограничено. Реальные компиляторы не с

¹ В том, что эти два класса грамматик несопоставимы, можно убедится, рассмот приведенных примера — в них взяты различные по своей сути и классам грам хотя они и являются эквивалентными — задают один и тот же язык. ся на основе универсальных распознавателей из-за их высокой требовательности к необходимым вычислительным ресурсам. Как правило, конкретную КС-грам­матику и заданный ею КС-язык удается отнести к тому или иному классу, для которого существует специального рода распознаватель с линейной зависимо­стью требуемых вычислительных ресурсов от длины входной цепочки — линей­ный распознаватель.

Линейные распознаватели (распознаватели без возвратов) существуют и в виде восходящих, и в виде нисходящих распознавателей. И те и другие имеют линей­ную зависимость вычислительных ресурсов, необходимых для выполнения алго­ритмов разбора, от длины входной цепочки символов. Существуют также другие варианты линейных распознавателей, сочетающие в себе некоторые черты вос­ходящего и нисходящего разбора [6, т. 1].

Но возникает другой вопрос: очень часто одна и та же КС-грамматика может быть отнесена не к одному, а сразу к нескольким классам грамматик, допускаю­щих построение линейных распознавателей. Иногда для этого надо выполнить некоторые преобразования правил грамматики¹. В этом случае необходимо ре­шить, какой из нескольких возможных распознавателей выбрать для практиче­ской реализации.

Если можно выбрать один из двух явно сопоставимых по сложности распозна­вателей (например, распознаватели Ь11(1)-грамматик и грамматик предшество­вания можно сопоставить по объему управляющих таблиц, так как они исполь­зуют схожие алгоритмы работы), тогда ответ очевиден. Однако ответить на этот вопрос не всегда легко, поскольку могут быть построены два принципиально разных распознавателя, алгоритмы работы которых несопоставимы. В первую очередь речь идет именно о восходящих и нисходящих распознавателях: в осно­ве первых лежит алгоритм подбора альтернатив, в основе вторых — алгоритм «сдвиг-свертка».

На вопрос о том, какой распознаватель — нисходящий или восходящий — вы­брать для построения распознавателя, нет однозначного ответа. Эту проблему необходимо решать, опираясь на некую дополнительную информацию о том, как будут использованы или каким образом будут обработаны результаты работы распознавателя. Тут следует вспомнить, что распознаватель входных цепочек КС-языков — это всего лишь один из этапов компиляции, составная часть ком­пилятора, лежащая в основе синтаксического анализатора входного языка про­граммирования. И с этой точки зрения результаты работы распознавателя служат исходными данными для различных этапов компиляции: прежде всего синтакси­ческого анализа, затем — генерации кода. Поэтому выбор того или иного распо­знавателя во многом зависит от реализации компилятора, от того, какие принци­пы положены в его основу.

Восходящий синтаксический анализ, как правило, привлекательнее нисходяще­го, так как для данного языка программирования часто легче построить право-Примером такой грамматики может служить грамматика арифметических выражений, которая была впервые упомянута в разделе «Проблемы однозначности и эквивалентно­сти грамматик», глава 9, а потом многократно использовалась в качестве примера для ил­люстрации работы различных распознавателей.

сторонний (восходящий) распознаватель на основе правоанализируемой гра матики. С этим вопросом мы уже сталкивались в данном пособии, когда говори о том, что класс языков, заданных LR-грамматиками, шире, чем класс язык< заданных LL-грамматиками (хотя следует сказать, что не все здесь столь од* значно).

С другой стороны, как будет показано далее, левосторонний (нисходящий) синт; сический анализ предпочтителен с точки зрения процесса трансляции, посколь на его основе легче организовать процесс порождения цепочек результируклщ языка. Ведь в задачу компилятора входит не только распознать (проанализи! вать) входную программу на входном языке, но и построить (синтезировать) ] зультирующую программу. Более подробную информацию об этом можно noj чить в разделе «Генерация кода. Методы генерации кода», глава 14 или в рабоп [6, т. 2, 42]. Левосторонний анализ, основанный на нисходящем распознавате оказывается предпочтительным также при учете вопросов, связанных с обна] жением и локализацией ошибок в тексте исходной программы [40, 82].

Желание использовать более простой класс грамматик для построения paci знавателя может потребовать каких-то манипуляций с заданной грамматик необходимых для ее преобразования к требуемому классу. При этом нере; грамматика становится неестественной и мало понятной, что в дальнейш затрудняет ее использование в схеме синтаксически управляемого перевод; трансляции на этапе генерации результирующего кода (см. главу «Генераци: оптимизация кода»). Поэтому часто бывает удобным использовать исходи грамматику такой, какая она есть, не стремясь преобразовать ее к более прос му классу.

В целом следует отметить, что с учетом всего сказанного выше, интерес пр ставляют как левосторонний, так и правосторонний анализ. Конкретный вы! зависит от реализации конкретного компилятора, а также от сложности грам тики входного языка программирования.

Отношения между классами КС-грамматик

В данном учебном пособии было рассмотрено несколько основных классов I грамматик, для которых существуют линейные распознаватели, — это LL-rp матики, LR-грамматики и грамматики предшествования. Не все они были { смотрены достаточно подробно, к тому же этими классами далеко не исчерпь ется список всех известных КС-грамматик такого рода. Можно еще, например, упомянуть класс грамматик ограниченного правого в текста (m,n) — ОПК(т,п). Это грамматики, допускающие построение распозн; теля, основанного на алгоритме «сдвиг-свертка», в котором однозначный вы между сдвигом и сверткой делается исходя из анализа m символов, находящи на верхушке стека, и п текущих символов входной цепочки, считая от поло ния считывающей головки расширенного МП-автомата [6, т. 1]. Все ОПК(т грамматики для всех значений тип составляют класс О ПК-грамматик. Г стейшим вариантом грамматик такого класса являются ОПК(1,1)-граммат1 Интересно, что с помощью этих грамматик, как и с помощью LR-грамма' можно определить любой детерминированный КС-язык. Далее в этом пункте будут рассмотрены различные классы КС-грамматик и су­ществующие между ними нетривиальные соотношения.

В общем случае можно выделить правоанализируемые и левоанализируемые КС-грамматики. Об этих двух принципиально разных классах грамматик уже гово­рилось выше: первые предполагают построение левостороннего (восходящего) распознавателя, вторые — правостороннего (нисходящего). Это вовсе не значит, что для КС-языка, заданного, например, некоторой левоанализируемой грамма­тикой, невозможно построить расширенный МП-автомат, который порождает правосторонний вывод. Указанное разделение грамматик относится только к по­строению на их основе детерминированных МП-автоматов и детерминированных расширенных МП-автоматов. Только эти типы автоматов представляют интерес при создании компиляторов и анализе входных цепочек языков программирова­ния. Недетерминированные автоматы, порождающие как левосторонние, так и правосторонние выводы, можно построить в любом случае для языка заданного любой КС-грамматикой, но для создания компилятора такие автоматы интереса не представляют (см. раздел «Распознаватели КС-языков. Автоматы с магазин­ной памятью», глава 11).

На рис. 12.10 изображена условная схема, дающая представление о соотношении классов левоанализируемых и правоанализируемых КС-грамматик [5,6, т. 2,42,65].

лг
						ПГ
					LR
			LL

Рис. 12.10. Соотношение классов левоанализируемых и правоанализируемых КС-грамматик

Интересно, что классы левоанализируемых и правоанализируемых грамматик являются несопоставимыми. То есть существуют левоанализируемые КС-грам­матики, на основе которых нельзя построить детерминированный расширенный МП-автомат, порождающий правосторонний вывод; и наоборот — существуют правоанализируемые КС-грамматики, не допускающие построение МП-автома­та, порождающего левосторонний вывод. Конечно, существуют грамматики, под­падающие под оба класса и допускающие построение детерминированных авто­матов как с правосторонним, так и с левосторонним выводом.

Следует помнить также, что все упомянутые классы КС-грамматик — это счет­ные, но бесконечные множества. Нельзя построить и рассмотреть все возмож­ные левоанализируемые грамматики или даже все возможные LL(^-граммати­ки. Сопоставление классов КС-грамматик производится исключительно на основе анализа структуры их правил. Только на основании такого рода анализа произ­вольная КС-грамматика может быть отнесена в тот или иной класс (или не­сколько классов).

Все это тем более интересно, если вспомнить, что рассмотренный в данном пс бии класс левоанализируемых LL-грамматик является собственным подмно ством класса LR-грамматик: любая LL-грамматика является LR-грамматщ но не наоборот — существуют LR-грамматики, которые не являются LL-грам тиками. Этот факт также нашел свое отражение в схеме на рис. 12.10. Зна¹ любая LL-грамматика является правоанализируемой, но существуют так» другие левоанализируемые грамматики, не попадающие в класс правоанал! руемых грамматик.

Для LL(k)-rpaMMaTHK, составляющих класс LL-грамматик, интересна еще с особенность: доказано, что всегда существует язык, который может быть з< LL(k)-rpaMMaTHKoft для некоторого к > 0, но не может быть задан LL(k-l)-r] матикой. Таким образом, все LL(k)-rpaMMaraKH для всех к представляют о: деленный интерес (другое дело, что распознаватели для них при больших зн ниях к будут слишком сложны). Интересно, что проблема эквивалентности двух LL(k)-rpaMMaraK разрешима.

С другой стороны, для LR(k)-rpaMMaTHK, составляющих класс LR-грамма доказано, что любой язык, заданный LR(k)-rpaMMaTHKoft с к > 1, может быт дан LR(l)-rpaMMaTHKoft. То есть LR(k)-rpaMMaTHKH с к > 1 интереса не преде ляют. Однако доказательство существования LR(l)-rpaMMaTHKH вовсе не озна что такая грамматика всегда может быть построена (проблема преобразов; КС-грамматик неразрешима).

На рис. 12.11 условно показана связь между некоторыми классами КС-гра тик, упомянутых в данном пособии. Из этой схемы видно, например, что Л1 ОПК-грамматика является LR-грамматикой, а также любая LL-грамматика s ется LR-грамматикой, но не всякая LL-грамматика является LR(l)-rpaMMaTH

КС- грамматики

Однозначные

ОПК

LR(1)

Операторного предшествования

(1,1)ОПК

Рис. 12.11. Схема взаимосвязи некоторых классов КС-грамматик

Если вспомнить, что любой детерминированный КС-язык может быть задан, например, Ы1(1)-грамматикой (или ОПК(1,1)-грамматикой), но в то же время, классы левоанализируемых и правоанализируемых грамматик несопоставимы, то напрашивается вывод: один и тот же детерминированный КС-язык может быть задан двумя или более несопоставимыми между собой грамматиками. Та­ким образом, можно вернуться к мысли о том, что проблема преобразования КС-грамматик неразрешима (на самом деле, конечно, наоборот: из неразрешимости проблемы преобразования КС-грамматик следует возможность задать один и тот же КС-язык двумя несопоставимыми грамматиками). Это, наверное, самый ин­тересный вывод, который можно сделать из сопоставления разных классов КС-грамматик.

Отношения между классами КС-языков

КС-язык называется языком некоторого класса КС-языков, если он может быть задан КС-грамматикой из данного класса КС-грамматик. Например, класс LL-языков составляют все языки, которые могут быть заданы с помощью LL-грам-матик.

Соотношение классов КС-языков представляет определенный интерес, оно не сов­падает с соотношением классов КС-грамматик. Это связано с многократно уже упоминавшейся проблемой преобразования грамматик. Например, выше уже говорилось о том, что любой LL-язык является и Ы1(1)-языком — то есть язык, заданный LL-грамматикой, может быть задан также и Ъ11(1)-грамматикой. Одна­ко не всякая LL-грамматика является при этом LR(l)-rpaMMaraKOU и не всегда можно найти способ, как построить LR(l)-rpaMMaTHKy, задающую тот же самый язык, что и исходная LL-грамматика.

На рис. 12.12 приведено соотношение между некоторыми известными классами КС-языков [6, т. 2, 42, 47].

КС-языки

Детерминированные КС-языки LR(1 )-языки=1_К-языки (1,1)ОПК-языки=ОПК-языки

Языки простого предшествования
				LL-языки
	Языки операторного предшествования

Рис. 12.12. Соотношение между различными классами КС-языков

Следует обратить внимание прежде всего на то, что интересующий разработ­чиков компиляторов в первую очередь класс детерминированных КС-языков полностью совпадает с к«лассом LR-языков и, более того, совпадает с кл; LR(l)^3biKOB. To есть досказано, что для любого детерминированного КС-! существует задающая его_о LR(1) -грамматика. Этот факт уже упоминался i Проблема состоит в том,; что не всегда возможно найти такую грамматику формализованного алгоритма, как ее построить в общем случае. То же сам< носится к упоминавшимсся здесь ОПК-грамматикам и ОПК(1,1)-грамматю Также уже упоминалось,,, _чт0 LL-языки являются собственным подмноже. LR-языков: всякий LL-яззык является одновременно LR-языком, но сущеа LR-языки, которые не являются LL-языками. Поэтому LL-языки образуют узкий класс, чем LR-язьцки.

Языки простого предшествования, в свою очередь, также являются собстве: подмножеством LR-языкссов, а языки операторного предшествования — собс ным подмножеством язы,_1Ков простого предшествования. Интересно, что * операторного предшествования представляют собой более узкий класс, чем ки простого предшествовзания.

В то же время языки простого предшествования и LL-языки несопоставим жду собой: существуют я_?3ыки простого предшествования, которые не явл5 LL-языками, и в то же вр<,емя существуют LL-языки, которые не являются я: ми простого предшествовзания. Однако существуют языки, которые одновр но являются и языками Простого предшествования, и LL-языками. Аналог] замечание относится так_СЖе к соотношению между собой языков операто] предшествования и LL-H<3biKOB.

Можно еще отметить, чтс_э язык арифметических выражений над символами заданный грамматикой G(^{+,-,/,*,a,b},{S,T,E},P,S), P = {S->S+T|S-T|T, T->T*Ef E-»(S)|a|b}, который многократно использовался в примерах в данном уче пособии, подпадает под Bj_Ce указанные выше классы языков. Из приведеннь нее по всей главе 3 призеров можно заключить, что этот язык является \ языком, и языком операторного предшествования, а следовательно, и яз простого предшествования и, конечно, LR(l)^3biKOM. В то же время этот по мере изложения материала пособия описывался различными граммати не все из которых могут (быть отнесены в указанные классы. Более того, в п он был задан с помощью, грамматики, которая не являлась даже однозначн

Таким образом, соотнощение классов КС-языков не совпадает с соотноше задающих их классов К(3-грамматик. Это связано с неразрешимостью прс преобразования и эквивгшентности грамматик, которые не имеют строго ф| . лизованного решения.