
18.2.3. Свойства равномерно сходящихся рядов.
18.2.3.1. Теорема о непрерывности суммы
равномерно сходящегося ряда непрерывных
функций. Если члены функционального
ряда
![]() - непрерывные функции, и этот ряд
равномерно сходится на отрезке
- непрерывные функции, и этот ряд
равномерно сходится на отрезке
![]() ,
то сумма этого ряда непрерывна на
,
то сумма этого ряда непрерывна на
![]() .
.
18.2.3.2. Теорема о почленном интегрировании
равномерно сходящегося ряда. Пусть
члены функционального ряда непрерывны
на отрезке
![]() ,
и ряд равномерно сходится к своей сумме
,
и ряд равномерно сходится к своей сумме
![]() на этом отрезке:
на этом отрезке:
![]() .
Тогда
.
Тогда
![]() ,
т.е. интеграл от суммы ряда равен сумме
ряда, составленного из интегралов от
членов равномерно сходящегося ряда.
,
т.е. интеграл от суммы ряда равен сумме
ряда, составленного из интегралов от
членов равномерно сходящегося ряда.
18.2.3.3. Теорема о почленном дифференцировании
равномерно сходящегося ряда. Пусть
члены сходящегося ряда
![]() - дифференцируемые на отрезке
- дифференцируемые на отрезке
![]() функции, и ряд, составленный из производных
функции, и ряд, составленный из производных
![]() ,
равномерно сходится на
,
равномерно сходится на
![]() .
Тогда ряд
.
Тогда ряд
![]() можно почленно дифференцировать, и
можно почленно дифференцировать, и
![]() ,
т.е. производная суммы ряда равна сумме
ряда из производных.
,
т.е. производная суммы ряда равна сумме
ряда из производных.
Отметим тонкость, заключённую в этой теореме: для того, чтобы ряд можно было почленно дифференцировать, требуется равномерная сходимость не самого этого ряда, а ряда, составленного из производных его членов.
Эти свойства равномерно сходящихся
рядов по нашей программе принимаются
без доказательства; мы будем ими
пользоваться при изучении степенных
рядов. Однако уже сейчас мы можем сделать
из этих теорем тонкие и важные выводы.
Ряд
![]() - геометрическая прогрессия со знаменателем
- геометрическая прогрессия со знаменателем
![]() ,
поэтому его сумма равна
,
поэтому его сумма равна
![]() :
:
![]() .
Мы доказали, что этот ряд равномерно
сходится на любом отрезке
.
Мы доказали, что этот ряд равномерно
сходится на любом отрезке
![]() ,
целиком лежащем в области сходимости
(-1,1), поэтому его можно почленно
проинтегрировать в пределах от 0 до
,
целиком лежащем в области сходимости
(-1,1), поэтому его можно почленно
проинтегрировать в пределах от 0 до
![]() :
:
![]() .
Вычисляя интегралы, получаем
.
Вычисляя интегралы, получаем
![]()
![]() .
Это не только неожиданное и красивое
представление числа
.
Это не только неожиданное и красивое
представление числа
![]() в виде ряда
в виде ряда
![]() ,
но и удобный способ его вычисления с
любой точностью с простой оценкой
остатка по первому отброшенному члену,
так как получен ряд Лейбницевского типа
(см. раздел 18.1.4.2).
,
но и удобный способ его вычисления с
любой точностью с простой оценкой
остатка по первому отброшенному члену,
так как получен ряд Лейбницевского типа
(см. раздел 18.1.4.2).
Степенные ряды.
18.2.4.1. Определение. Степенным рядом
называется функциональный ряд вида
![]() ,
,
где
![]() - постоянные (коэффициенты ряда),
- постоянные (коэффициенты ряда),
![]() - фиксированное число (центр сходимости).
Степенной ряд имеет по меньшей мере
одну точку сходимости - точку
- фиксированное число (центр сходимости).
Степенной ряд имеет по меньшей мере
одну точку сходимости - точку
![]() .
.
Все содержательные сведения о степенном ряде содержатся в теореме Абеля.
18.2.4.2. Теорема Абеля. Если степенной
ряд сходится в точке
![]() ,
то
,
то
-
он абсолютно сходится в любой точке х, удовлетворяющей неравенству
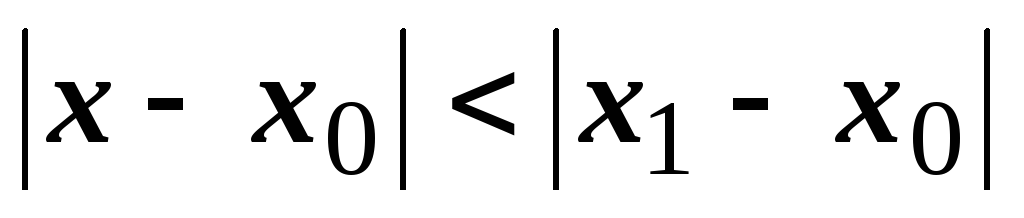 (т.е. находящейся ближе к точке
(т.е. находящейся ближе к точке
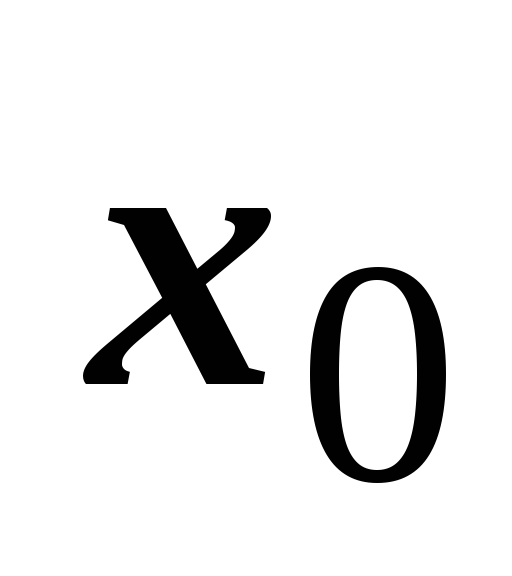 ,
чем
,
чем
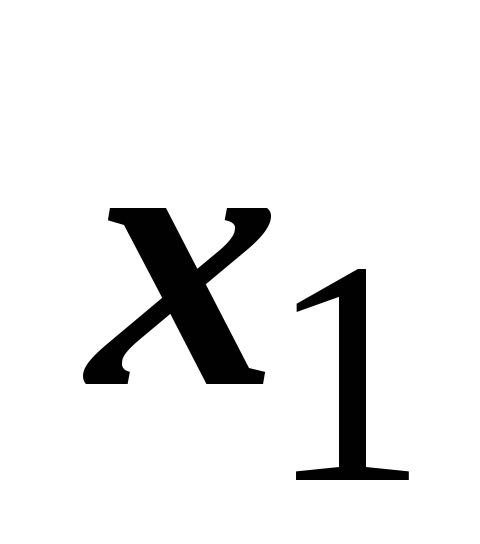 );
); -
он сходится равномерно на любом отрезке
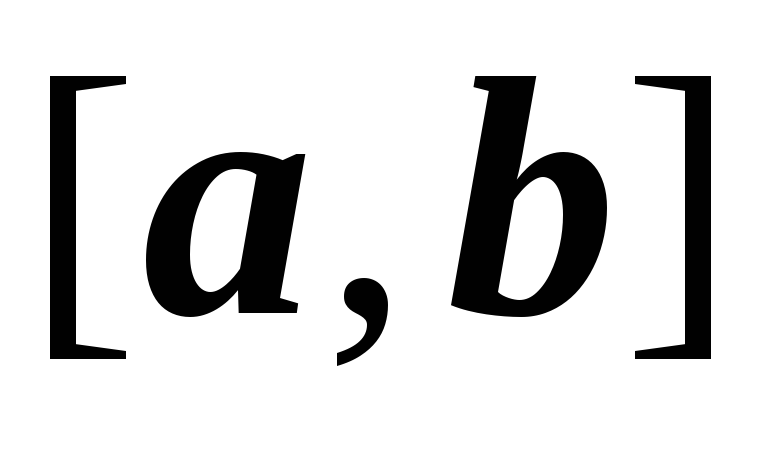 ,
целиком лежащем на интервале
,
целиком лежащем на интервале
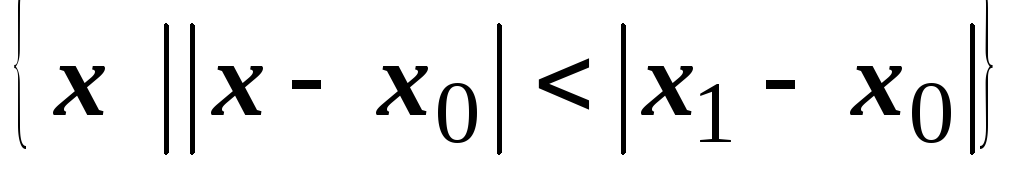 (т.е. на интервале с центром в
(т.е. на интервале с центром в
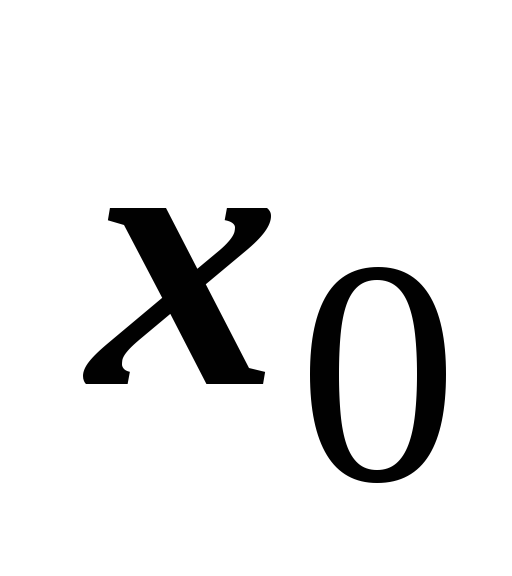 радиуса
радиуса
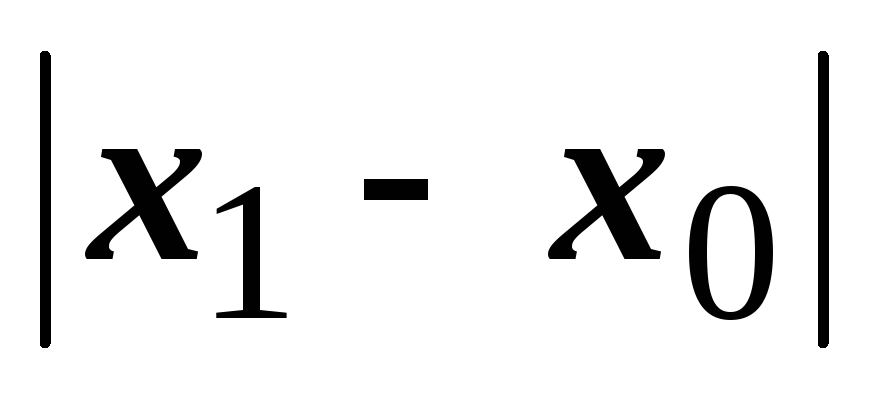 ).
). -
Если этот ряд расходится в точке
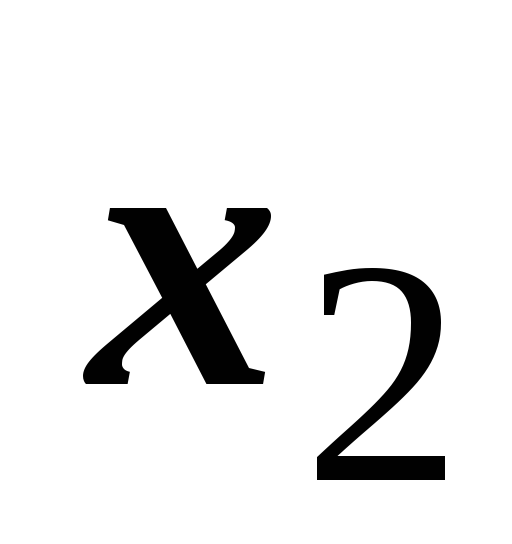 ,
то он расходится в любой точке х,
удовлетворяющей неравенству
,
то он расходится в любой точке х,
удовлетворяющей неравенству
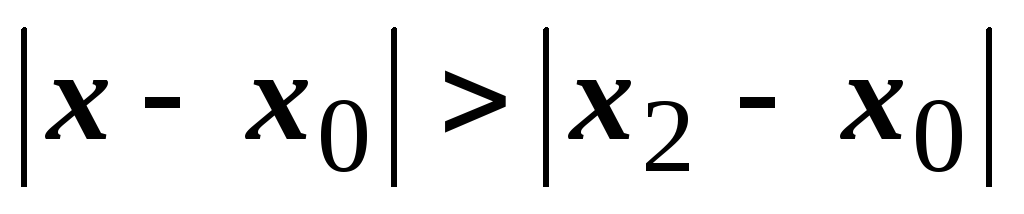 (т.е. находящейся дальше от точки
(т.е. находящейся дальше от точки
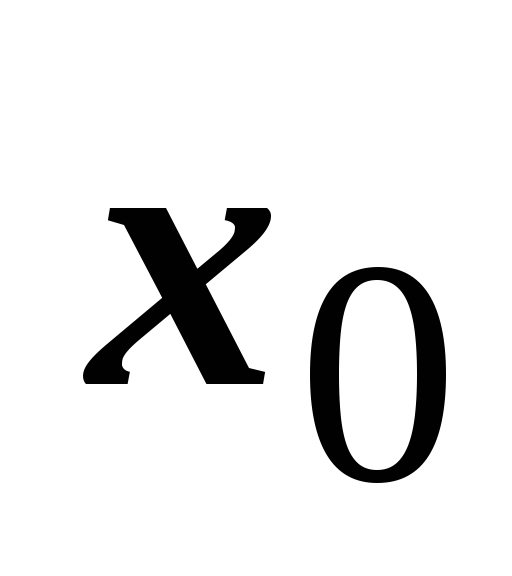 ,
чем
,
чем
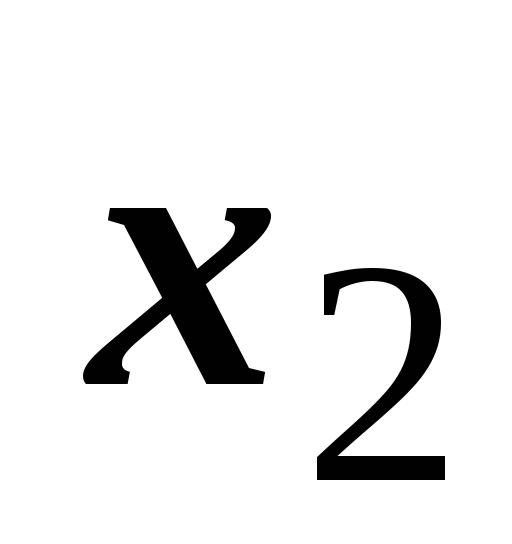 ).
).
 Доказательство.
1. Из сходимости ряда
Доказательство.
1. Из сходимости ряда
![]() в точке
в точке
![]() следует, что его общий член
следует, что его общий член
![]() стремится к нулю при
стремится к нулю при
![]() ;
любая последовательность, имеющая
предел, ограничена, следовательно,
существует число С такое, что
;
любая последовательность, имеющая
предел, ограничена, следовательно,
существует число С такое, что
![]() .
Пусть точка х удовлетворяет
неравенству
.
Пусть точка х удовлетворяет
неравенству
![]() ,
тогда
,
тогда
![]() .
Оценим член ряда в точке х:
.
Оценим член ряда в точке х:
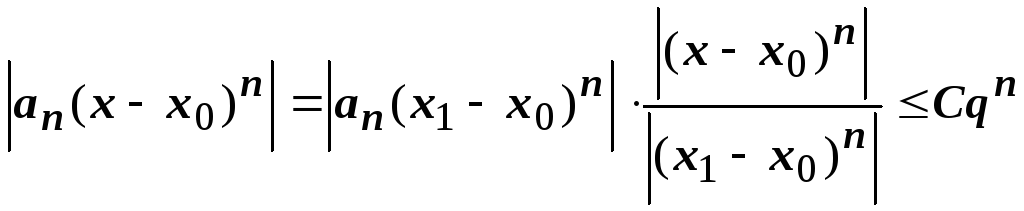 .
Члены ряда в точке х по абсолютной
величине не превосходят членов сходящейся
геометрической прогрессии, следовательно,
ряд сходится абсолютно в точке х,
следовательно, он сходится абсолютно
в любой точке интервала
.
Члены ряда в точке х по абсолютной
величине не превосходят членов сходящейся
геометрической прогрессии, следовательно,
ряд сходится абсолютно в точке х,
следовательно, он сходится абсолютно
в любой точке интервала
![]() .
.
2. Пусть отрезок
![]() ,
целиком лежит на интервале
,
целиком лежит на интервале
![]() .
Из точек а, b
выберем ту, которая находится дальше
от точки
.
Из точек а, b
выберем ту, которая находится дальше
от точки
![]() ,
примем для определённости, что это -
точка а:
,
примем для определённости, что это -
точка а:
![]() .
Тогда для любого х из этого отрезка
.
Тогда для любого х из этого отрезка
![]() .
В точке
.
В точке
![]() ряд
ряд
![]() ,
по доказанному, сходится абсолютно, но
он является на
,
по доказанному, сходится абсолютно, но
он является на
![]() мажорантой для ряда
мажорантой для ряда
![]() ,
следовательно, степенной ряд сходится
равномерно на отрезке
,
следовательно, степенной ряд сходится
равномерно на отрезке
![]() .
.
3. Пусть степенной ряд расходится в
точке
![]() ,
и
,
и
![]() .
То, что ряд расходится в точке х,
докажем от противного. Если предположить,
что он сходится в точке х, то, по
доказанному, он сходится во всех точках,
расположенных ближе к
.
То, что ряд расходится в точке х,
докажем от противного. Если предположить,
что он сходится в точке х, то, по
доказанному, он сходится во всех точках,
расположенных ближе к
![]() ,
чем х, следовательно, он сходится
в точке
,
чем х, следовательно, он сходится
в точке
![]() ,
что противоречит условию.
,
что противоречит условию.
 18.2.4.3.
Радиус сходимости, интервал сходимости
и область сходимости степенного ряда.
Из теоремы Абеля следует, что существует
такое число R
18.2.4.3.
Радиус сходимости, интервал сходимости
и область сходимости степенного ряда.
Из теоремы Абеля следует, что существует
такое число R
![]() (возможно,
(возможно,
![]() )
такое, что при
)
такое, что при
![]() степенной ряд сходится, при
степенной ряд сходится, при
![]() ряд расходится. Действительно, пусть в
точке
ряд расходится. Действительно, пусть в
точке
![]() ряд сходится, в точке
ряд сходится, в точке
![]() ряд расходится. Рассмотрим точку
ряд расходится. Рассмотрим точку
![]() ,
расположенную между областями, в которых
установлена сходимость и расходимость.
В точке
,
расположенную между областями, в которых
установлена сходимость и расходимость.
В точке
![]() числовой ряд
числовой ряд
![]() либо сходится, либо расходится. Если он
сходится, то мы можем перенести точку
либо сходится, либо расходится. Если он
сходится, то мы можем перенести точку
![]() в точку
в точку
![]() ;
если ряд в точке
;
если ряд в точке
![]() расходится, мы переносим в
расходится, мы переносим в
![]() точку
точку
![]() .
Продолжая этот процесс, мы сблизим точки
.
Продолжая этот процесс, мы сблизим точки
![]() и
и
![]() ,
эта граница и определит число R.
,
эта граница и определит число R.
Определение. Число R
![]() такое, что при
такое, что при
![]() степенной ряд сходится, при
степенной ряд сходится, при
![]() ряд расходится, называется радиусом
сходимости. Интервал
ряд расходится, называется радиусом
сходимости. Интервал
![]() называется интервалом сходимости
степенного ряда.
называется интервалом сходимости
степенного ряда.
Сходимость ряда в концевых точках
интервала сходимости должна исследоваться
отдельно. В зависимости от поведения
ряда на концах интервала сходимости
область сходимости степенного ряда
может быть одной из следующих:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Итак, для определения области сходимости
степенного ряда надо найти его интервал
сходимости R, затем
исследовать поведения ряда в концевых
точках интервала сходимости
![]() .
.
Свойства степенного ряда и его суммы.
