2. Градиент

Пусть функция u=f(x,y,z) определена и дифференцируема на множестве G.

Определение. Градиентом функции u=f(x,y,z) в точке М₀ называется вектор с координатами .

Обозначается или .

Итак, .

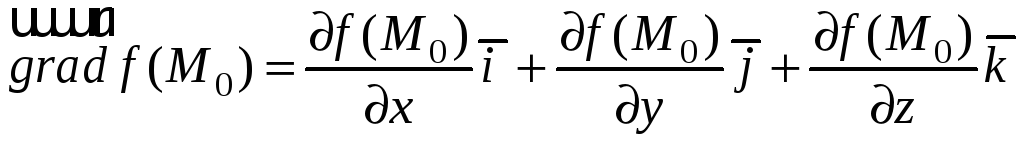Если функция f дифференцируема на G, то в каждой точке МG определён вектор . В этом случае говорят, что градиент функции f образует векторное поле на G, и оно называется векторным полем градиентов.

Теорема. Если функция u=f(x,y,z) дифференцируема в точке М₀, то производная по направлению l в точке М₀ равна проекции градиента функции f в этой точке на направление l.

Доказательство.

Т.к. функция f дифференцируема в точке М₀, то в этой точке существуют производная по направлению l и градиент, т.е. имеем

,

.

Ч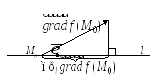ерез обозначим единичный вектор направления l: .

Тогда (скалярное произведение).

Т.к. , где - угол между векторами и , то, учитывая, что а , получим . Следовательно, .

Свойства градиента

1. Производная в данной точке М₀ по направлению l имеет наибольшее значение, если направление l совпадает с направлением градиента. Это наибольшее значение

.

Доказательство.

.

Ясно, что имеет наибольшее значение, когда , т.е. когда φ=0. Это означает, что направление совпадает с направлением .

2. Производная по направлению вектора, перпендикулярного к вектору градиента, равна нулю (следует из доказательства теоремы).

3. В каждой точке М₀ области определения функции градиент функции f направлен по нормали к поверхности уровня проходящей через эту точку.

4. ;

5. , где с=const;

6.

Свойства 4-6 следуют из определения градиента и правил дифференцирования.

§7. Производные и дифференциалы высших порядков

1. Частные производные высших порядков

Пусть функция z =f(x,y) задана на области G. Пусть на G существуют частные производные и . Они называются частными производными первого порядка функции f . Эти производные на G являются функциями от x и y: , . Они тоже могут иметь частные производные G. Частные производные этих функций φ и ψ называются частными производными второго порядка функции f:

,

,

,

.

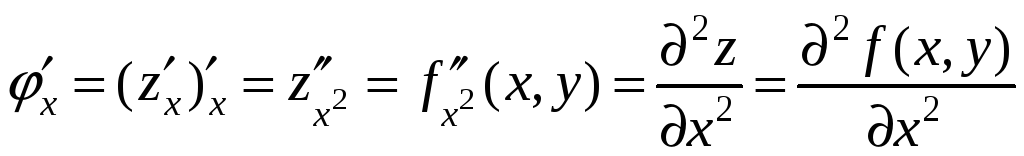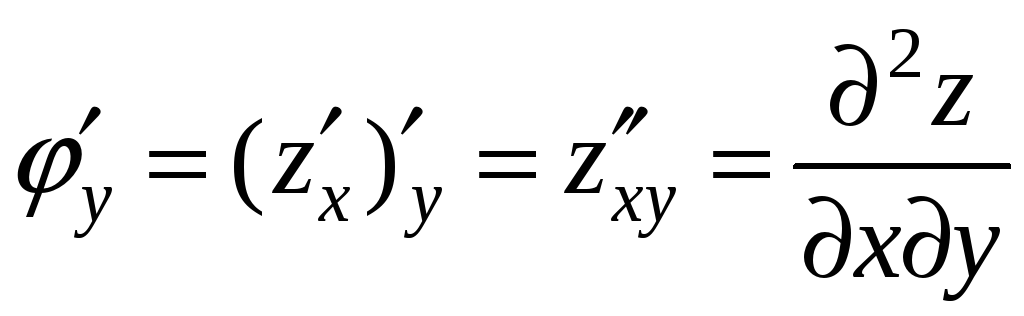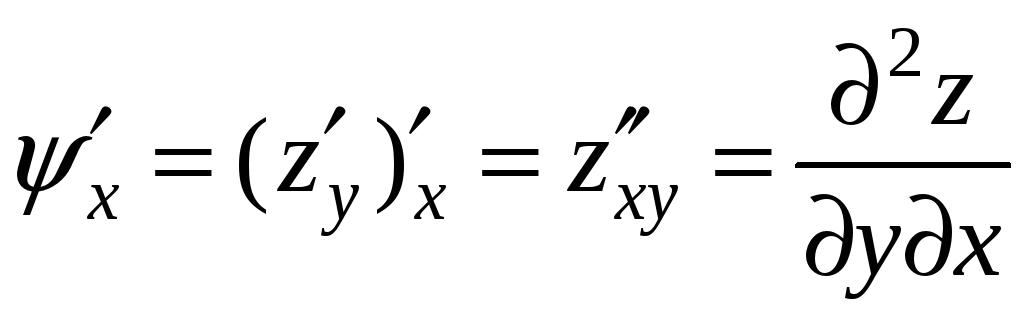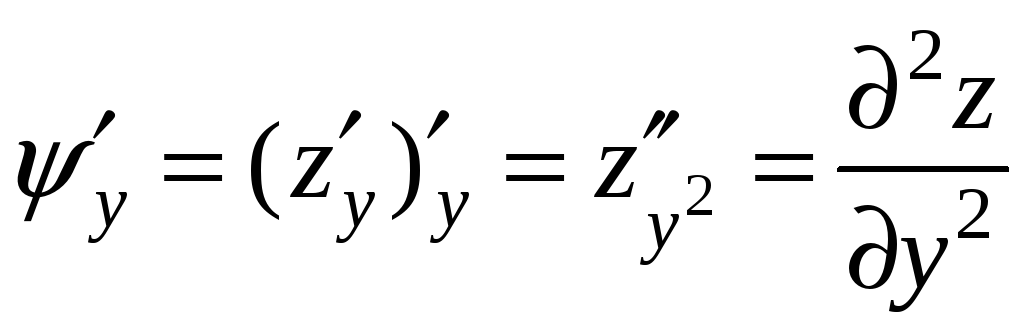Частные производные и взяты по различным переменным, они называются смешанными. Если частные производные второго порядка определены на G, то они сами являются функциями от x и y и могут иметь частные производные по этим переменным. Частные производные от частных производных второго порядка называются частными производными третьего порядка функции f и обозначаются:

(8 штук, 6 смешанных).

Аналогично определяются частные производные и более высоких порядков. Если известны частные производные (n-1)-го порядка, то частные производные от этих частных производных называются частными производными п-го порядка и обозначаются:

Т.о., частные производные высших порядков определяются индуктивно, т.е. последовательно, начиная от первой.

Частные производные и взяты по одним и тем же переменным, но в разном порядке. Они не обязательно равны!

Теорема 1. Пусть функция z =f(x,y) и ее частные производные определены в некоторой окрестности точки (х₀;у₀), и в этой точке и непрерывны. Тогда .

Доказательство.

Придадим значениям х₀ и у₀ приращения Δх и Δу так, чтобы точка (х₀+Δх;у₀+Δу) находилась в окрестности точки (х₀;у₀). Составим выражение

.

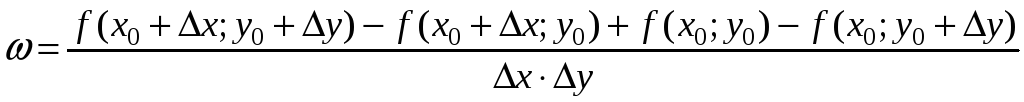Чтобы легче запомнить, как строится выражение, рассмотрим прямоугольник АBСD с вершинами А(х₀+Δх;у₀+Δу), B(х₀+Δх;у₀), С(х₀;у₀), D(х₀;у₀+Δу). Тогда числитель равен алгебраической сумме значений функции f(x,y) в вершинах прямоугольника, причем значение в точке А берется со знаком «+», и при обходе прямоугольника по часовой стрелке знаки перед остальными слагаемыми чередуются.

Введем вспомогательную функцию

.

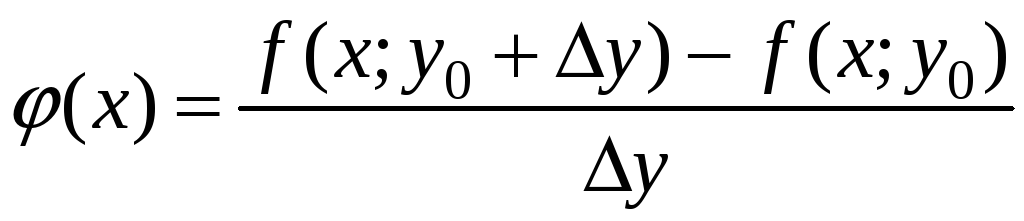Здесь числитель равен разности значений функции f(x,y) в точках сторон АD и ВС с одинаковыми абсциссами. Тогда ω можно записать в виде:

=

.

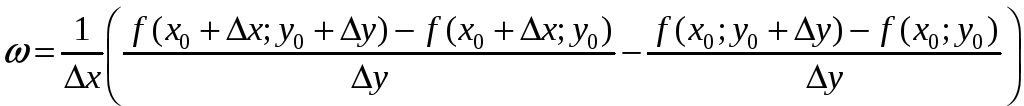По условию существует , значит, существует и

.

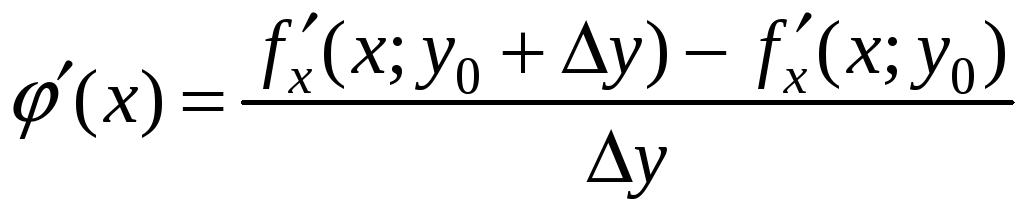Т.к. функция φ(х) дифференцируема на отрезке [x₀;x₀+Δx], то она непрерывна на этом отрезке. Следовательно, к ней можно применить формулу Лагранжа:

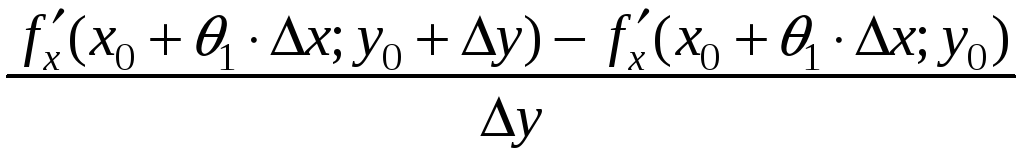=, где . (1)

Т.к. по условию существует и , то к функции , как к функции от у, на отрезке [у₀;у₀+Δу] можно тоже применить формулу Лагранжа:

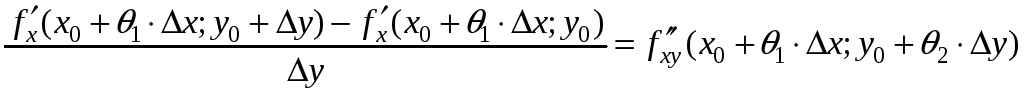, (2)

где . Тогда из (1) и (2) следует

, где . (3)

Теперь вместо функции φ(х) рассмотрим функцию

.

Тогда

=

.

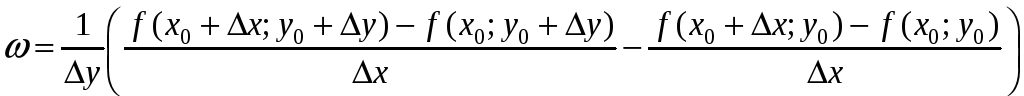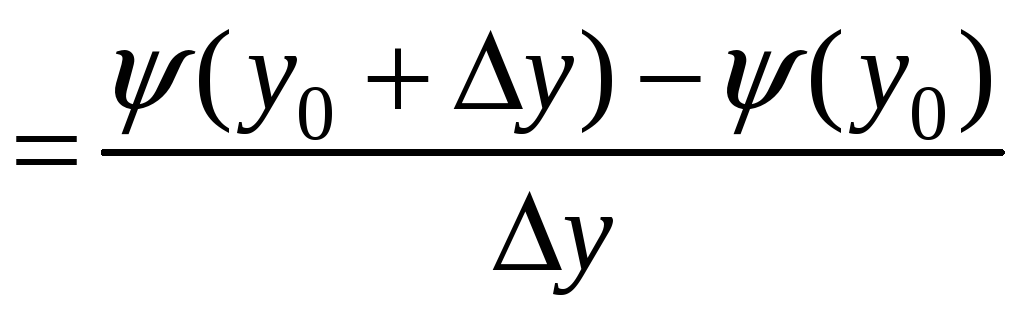Применим формулу Лагранжа к функции ψ(у)на отрезке [у₀;у₀+Δу]:

,

а затем к функции , как к функции от х, на отрезке [x₀;x₀+Δx]:

, где . (4)

Из соотношений (3), (4) следует

. (5)

Пусть . Тогда

, .

Т.к. по условию и непрерывны в точке (х₀;у₀), то

и

.

Тогда, переходя в равенстве (5) к пределу при , получим

.

Замечание. Утверждение, аналогичное теореме 1, может быть доказано и для смешанных производных любого порядка. Т.е. смешанные производные любого порядка при условии их непрерывности не зависят от порядка дифференцирования, например,

.

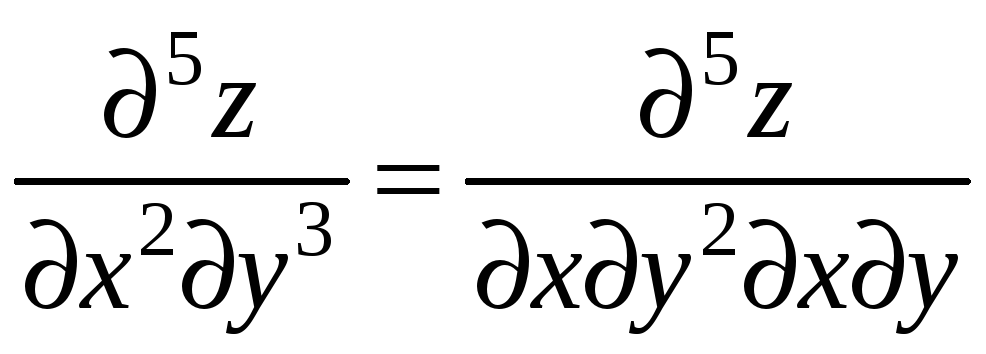Теорема 2. Если смешанные производные n – го порядка, отличающиеся только порядком дифференцирования, непрерывны на области G, то они на этой области равны.