§2. Алгебраические критерии устойчивости

Алгебраические критерии устойчивости позволяют судить об ус­тойчивости системы по коэффициентам характеристического уравнения:

D(s) =a₀ S²+a₁S²+...+a_n=0. (1)

Заметим, что необходимым условием устойчивости системы любого порядка является положительность всех коэффициентов характеристического уравнения

(1):

a₀>0;а₁>0,...,а_n >0 (2)

В соответствии с теоремой Безу уравнение (1) можно представить в виде произведения множителей, содержащих корпи s₁,s₂,...,s_n;

a₀(s-s₁)(s-s₂)...(s-s_n)=0

Бели все корни характеристического уравнения будут отрицательны, то ко­эффициенты уравнения (1) будут положительны.

Критерий устойчивости Рауса.

В 1877 г оду английский математик Э. Раус для определения устойчивости системы по коэффициентам характеристического уравнения (1) предложил правило, оформленное в виде таблицы.

Таблица Рауса. Таблица

I.

Коэффициенты	a0	a2	a4	a6
	a1	a3	а5	а7
	С13= а2-r0 –а3	С23=а4-r0a5	С33 =а6-r0a7	С43= а8-r0a9
	С14=a3 – r1c23	C24=a5-r1c33	C34 = a7-r1c43	C44= a6-r1c53
	С15=c23 - r2 c24	С25= Сзз-r2 c34	С35:=С43 - r2С44	С45=С53-r2С54
...	...	...	...

После того как таблица Рауса заполнена, по ней можно судить об устойчивости системы. Условие устойчивости Рауса формулируется так: для устойчивости системы управления необходимо и достаточно, чтобы коэффициенты (числа) первого столбца таблицы Рауса были положительными: а₀>0; a₁>0; C₁₃>0;...;

C_ln+1>0.

Если не все коэффициенты первого столбца положительны, то система неустойчива, а число правых корней характеристического уравнения равно числу перемен знака в первом столбце таблицы Рауса.

Критерий устойчивости Гурвица

В 1895 году немецким математиком А. Гурвицем был разработан алгебраический критерий устойчивости в форме определителей, составляемых из коэффициентов характеристического уравнения системы.

Из коэффициентов характеристического уравнения (1) строят сначала главный определитель Гурвица по следующему правилу: по главной диагонали определителя слева направо выписывают все коэффициенты характеристического уравнения от а₁ | до а₃ в порядке возрастания индексов. Столбцы вверх от главной диагонали дополняют коэффициентами характеристического уравнения с последовательно возрастающими индексами, а столбцы вниз - коэффициентами с последовательно убывающими индексами. На место коэффициентов с индексами больше п и меньше нуля проставляют нули.

Отчеркивая в главном определителе Гурвица диагональные миноры, полу­чаем определители Гурвица низшего порядка:

a1	аъ	a5
а0	а2	а4
0	a1	a3

; и т.д. (4)

а_{ а_ъ

А, = а₁;Δ₂ =

Δ ₃= а₀ а₂

Критерий устойчивости Гурвица формулируется следующим образом: для того, чтобы система автоматического управления была устойчива, необходи­мо и достаточно, чтобы коэффициент при высшей степени, т.е. a₀ >0 и все определители Гурвица Δ_1,Δ₂,...,Δ_n были положительными.

Если все определители Гурвица низшего порядкаΔ₁,Δ₂,...,Δ_n-1, положительны, то система находится на границе устойчивости, когда главный определитель равен нулю:

Δn=a_n Δ_n-1 (5)

Последнее равенство возможно в двух случаях: а_n=0 или Δ_n-1= 0. В первом случае система находится на границе апериодической устойчивости (один из корней характеристического уравнения равен нулю); во втором случае на границе колебательной устойчивости (два комплексно-сопряженных корня ха­рактеристического уравнения находятся на мнимой оси).

Раскрывая определители Гурвица для характеристических уравнений первого, второго, третьего и четвертого порядков, можно получить следующие условия устойчивости:

1) Уравнение первого порядка.

a₀s+a₁=0

Для этого уравнения критерий Гурвица дает а₀>0,Δ₁ =а₁ >0.

2) Уравнение второго порядка. a₀ s² + а₁s + а₂ = 0

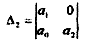
Для этого уравнения критерий Гурвица требует

a₀>0;

Δ₁=a₁ >0;

Δ ₂ = а₁ а₂> 0, Δ ₂= а₂ Δ₁> 0;

Последнее условие при наличии предшествующего эквивалентно условию

а₂>0.

Для устойчивости системы первого и второго порядков необходимо и дос­таточно, чтобы все коэффициенты характеристического уравнения системы были положительными. 3) Уравнение третьего порядка. a₀s³+a₁s²+a₂s+a₃=0.

ах	аъ	0
а0	а2	0
0	а1	аъ

Для ЭТОГО уравнения получаем условия

а₀>0,

Δ₁= а, > 0,

Δ ₂ =

a₁ а₃ = а_ха₂ -а₀а₃ >0,

Δ ₃ = а₃ Δ ₂ > 0.

Последнее условие при наличии предшествующего эквивалентно усло­вию а₃>0. Условие Δ ₂ > 0 при а₀>0, a₁>0, a₃>0, если а₂>0.

Для устойчивости системы третьего порядка необходимо и дос­таточно, чтобы все коэффициенты характеристического уравнения системы были положительными и определитель второго порядка Δ ₂ > 0.

Δ ₂ =а₁ а₂ -а₀а₃ >0.

(6)

Колебательная граница устойчивости Δ ₂ = 0.

4) Уравнение четвертого порядка. a₀s⁴ +a₁ s³ +а₂s² +а₃s + а₄ =0.

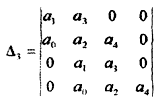
Для этого уравнения критерий Гурвица требует

a₁ > 0,

Δ₁= а₁ > 0,

Δ₂ =а₁а₂ -а₀а₃ >0,

Δ₃=-a₁(а₁а₃ -а₀0) + a₃(а₁а₂ -а₀а₃) = а₃ Δ₂ –а₁² a₄ >0,

Δ₄ = а₄ Δ₃ > 0. Если Δ₃ > 0,то а₄ > 0.

Условие Δ₃ > 0 при а₄ > 0, если а₃>0 и Δ₂ > 0.

Δ₂ > 0 при а₀ > 0, а₁ > 0, а₃ > 0, если а₂ > 0.

Для устойчивости системы четвертого порядка необходимо и доста­точно, чтобы все коэффициенты характеристического уравнения были по­ложительными и определитель третьего порядка Δ₃ > 0.

Колебательная граница устойчивости Δ₃ = 0.

5) Уравнение пятого порядка.

а₀ s⁵+a₁ s⁴ + а₂ s³ +a₂ s² +a₄ s + a₅ = 0.

(7)

Для уравнения пятого порядка, кроме положительности всех коэффициен­тов, должны выполняться еще два условия:

a₁ a₂-a₀a₃>0, (8)

(а₁ а₂-а ₀а₃ )(а₃ а₄ –а₂ а₅ )-(а₁ а₄ –а₄ а₅)²>0 (9)

Для уравнения пятой степени условия устойчивости по критерию Гурвица получаются достаточно громоздкими.

Можно установить, что система находится на колебательной границе устой­чивости при условии положительности всех миноров и равенства нулю предпо­следнего определителя Δ_n-1 = 0.