Модуль III. Ряды фурье

Тема № 9. Разложение в ряд Фурье функций на сегменте

Пусть функция y = f(x) задана на сегменте и удовлетворяет там условиям Дирихле. Чтобы разложить такую функцию в ряд Фурье, нужно её доопределить на сегменте . Тогда будем иметь возможность разложить f(x) в ряд Фурье. Так как реально заданной является только часть функции на сегменте

, то полученный ряд следует рассматривать лишь для переменной х, заданной в промежутке .

Очевидно, получившийся ряд будет зависеть от того, как именно мы произведём доопределение нашей первоначально заданной функции на .

Как доопределить функцию? Рассмотрим два варианта.

1. Продолжим функцию f(x) на промежуток чётным образом (см. рис. 7), т. е. построим новую функцию, обладающую свойством чётности (симметрия графика относительно оси оу) , которая на отрезке совпадает с функцией f(x). Тогда

  (14)

где .

Если х — точка непрерывности, то S(x) = f(x) для .

В точках конечного разрыва S(x) вычисляем соответственно теореме Дирихле.

2. Доопределим функцию f(x), продолжив её на отрезок нечётным образом, т. е. построим новую функцию, обладающую свойством нечётности (симметрия графика относительно начала координат) (см. рис. 8), которая на отрезке совпадает с функцией f(x), а именно: .

Тогда

(15)

где

В этом случае S(x) = f(x) во всех точках непрерывности функции отрезка .

Заключение. 1) В формулах (14) и (15) ряды Фурье для функций и f(x) будут совпадать только при .

2) Значения суммы ряда в конечных точках промежутка подсчитываем по теореме Дирихле, используя функцию, построенную для :

а) если продолжение (доопределение) — чётное (разложение только по косинусам), то

б) для нечётного продолжения (разложение только по синусам)

,

Пример 2. Разложить функцию f(x) = 2х - 2, в ряд Фурье, продолжив её  чётным образом;  нечётным образом.

Рис. 9

Решение. Продолжим функцию f(x) на интервал чётным образом (см. рис. 9), построив чётную функцию

Рис.  10

Ряд Фурье для чётной функции имеет вид

Ищем коэффициенты Фурье для функции :

Коэффициенты найдены. Составляем ряд:

Таким образом, полученный ряд сходится к функции f(x) для всех , т. е. S(x) = f(x) = 2х - 2, если .

б) Продолжим функцию f(x) на интервал нечётным образом (см. рис. 10), построив нечётную функцию

Ряд Фурье для нечётной функции имеет вид

Составляем ряд:

Таким образом, полученный ряд сходится к функции f(x) во всех внутренних точках промежутка , т. е. S(x) = f(x) = = 2х - 2, если .

 

В своё время на современников Фурье сильное впечатление производили разложения функций, подчиняющихся разным законам на разных промежутках, например, для функции, заданной графически (см. рис. 11), имеем разложение

Рис. 11

Фурье разлагал на промежутке чётную функцию cosx по синусам, нечётную функцию sinx по косинусам. Рассмотрим одну из подобных задач.

Упражнение. Разложите функцию (рис. 11) в ряд Фурье и убедитесь в правильности записанного разложения.

Пример 3. Разложить функцию y = xcosx по косинусам на промежутке . С помощью полученного разложения вычислить сумму ряда

Решение. Заметим, что на симметричном интервале (- е, е) данная функция является нечётной как произведение нечётной и чётной функций.

Продолжим нашу функцию на интервал чётным образом (см. рис. 12). Для подсчёта коэффициентов Фурье используем формулы (12):

b_n = 0,

Рис. 12

Интегрируем по частям

Подставив n = 0, вычислим

При п = 1 формула a_n не действует. Вычислим а₁ отдельно:

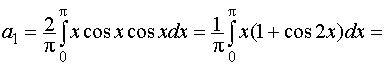
второе слагаемое интегрируем по частям, тогда

Все коэффициенты вычислены, можно записывать ряд Фурье для чётной функции , заданной на промежутке . Полученное разложение будет справедливо для функции y = xcosx во всех точках отрезка :

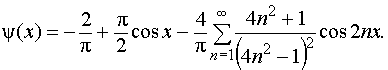
Теперь можно ответить на последний вопрос условия.

Выражение — числовой положительный ряд.

Покажем, что он сходится. Введём в рассмотрение сходящийся ряд с общим членом

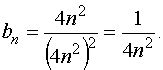
Используем обобщённый признак сравнения

Ряды ведут себя одинаково, т. е. оба сходятся и, следовательно, существует сумма ряда. Вычислим её, используя ряд Фурье. Подставим в полученное разложение х = 0: