
- •Глава 12. Элементы теории обыкновенных дифференциальных уравнений (оду)
- •12.1 Основные понятия и определения
- •12.2 Дифференциальные уравнения с разделяющимися переменными
- •12.3 Однородные и квазиоднородные уравнения
- •12.4 Линейные дифференциальные уравнения первого порядка
- •12.5 Дифференциальные уравнения в полных дифференциалах
- •12.6. Уравнения, не разрешенные относительно производной
- •12.7. Дифференциальные уравнения высших порядков
- •12.7.1 Основные понятия. Теорема Коши.
- •12.7.2. Уравнения, допускающие понижения порядка.
- •12.8. Линейные дифференциальные уравнения высших порядков
- •12.9. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
- •12.10. Линейные неоднородные дифференциальные уравнения
- •12.11. Метод неопределенных коэффициентов для определения частного решения неоднородного линейного уравнения с постоянными коэффициентами
- •12.12. Уравнение Эйлера. Системы линейных дифференциальных уравнений с постоянными коэффициентами (основные понятия)
- •12.13. Системы линейных дифференциальных уравнений первого порядка с постоянными коэффициентами
- •12.14. Системы линейных дифференциальных уравнений второго порядка с постоянными коэффициентами
- •12.15. Понятие решения
- •12.16. Уравнения с разделяющимися коэффициентами
- •12.17. Однородные уравнения
- •12.18. Линейные уравнения первого порядка
- •12.19. Уравнение Бернулли
- •12.20. Уравнения в полных дифференциалах
- •12.21. Уравнения вида
- •12.22. Уравнения вида
- •12.23. Линейные уравнения с постоянными коэффициентами
- •12.24. Принцип суперпозиции
- •12.25. Метод Лагранжа
- •Вопросы, упражнения и задачи к главе «Дифференциальные уравнения»
- •Тест для самоконтроля к главе «Дифференциальные уравнения»
12.21. Уравнения вида
Постановка задачи. Найти общее решение дифференциального уравнения
![]()
Алгоритм решения.
1. Полагая ![]() ,
получим дифференциальной уравнение
первого порядка
,
получим дифференциальной уравнение
первого порядка
![]()
2. Определяя тип
этого уравнения и применяя соответствующий
метод решения, находим ![]() где
где ![]() - произвольная постоянная.
- произвольная постоянная.
3. Так как ![]() ,
имеем
,
имеем
![]()
Последовательно
интегрируя ![]() раз (при каждом интегрировании не забывая
о произвольной постоянной), получим
ответ
раз (при каждом интегрировании не забывая
о произвольной постоянной), получим
ответ
![]()
![]() – произвольный постоянные.
– произвольный постоянные.
Пример 27. Найти общее решение дифференциального уравнения
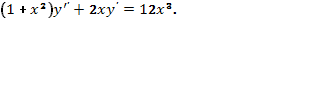
Решение.
1. поскольку
дифференциальное уравнение не содержит
у,
то полагая ![]() ,
имеем
,
имеем ![]() .
Получаем дифференциальное уравнение
первого порядка
.
Получаем дифференциальное уравнение
первого порядка
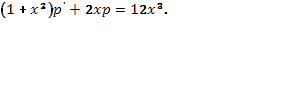
2. Уравнение
![]()
линейное относительно
![]() и
и ![]() .
Решая его, например, методом вариации
произвольной постоянной, находим
.
Решая его, например, методом вариации
произвольной постоянной, находим
![]()
3. Так как ![]() ,
имеем
,
имеем
![]()
Интегрируя, получим
общее решение ![]() .
.
Ответ. ![]() .
.
Условия задач. Найти общие решения дифференциальных уравнений.
1. ![]() .
Ответ:
.
Ответ: ![]()
2. ![]() Ответ:
Ответ: ![]()
12.22. Уравнения вида
Постановка задачи. Найти решение задачи Коши для дифференциального уравнения
![]()
с начальными условиями
![]()
Алгоритм решения.
1. Поскольку дифференциальное уравнение не содержит явно независимой переменной х, полагаем
![]()
где ![]() - новая неизвестная функция. Тогда по
формуле для произведения сложной функции
имеем
- новая неизвестная функция. Тогда по
формуле для произведения сложной функции
имеем
![]()
Получим уравнение
первого порядка относительно ![]()
![]()
2. Определяя тип
этого уравнения и применяя соответствующий
метод решения, находим ![]() ,
где С – произвольная постоянная.
,
где С – произвольная постоянная.
3. Используя
начальные условия (оба), находим ![]() .
.
4. Подставляя ![]() ,
получаем дифференциальное уравнение
с разделяющимися переменными
,
получаем дифференциальное уравнение
с разделяющимися переменными
![]()
Разделяя переменные
в области, где ![]() ,
получаем
,
получаем
![]()
и, интегрируя,
находим ![]() .
.
Проверяем, не
является ли решение ![]() особым решением исходного уравнения,
удовлетворяющим начальным условиям.
особым решением исходного уравнения,
удовлетворяющим начальным условиям.
5. Используем
начальные условия для нахождения второй
постоянной ![]() (значение
(значение ![]() уже найдено в п.3) и получаем решение
задачи Коши.
уже найдено в п.3) и получаем решение
задачи Коши.
Ответ записываем
в виде ![]() или
или ![]() .
.
Пример 28. Найти решение задачи Коши для дифференциального уравнения
![]()
с начальными
условиями ![]() .
.
Решение.
1. Поскольку дифференциальное уравнение не содержит явно независимой переменной х, полагаем
![]()
где ![]() – новая неизвестная функция. Тогда по
формуле для производной сложной функции
имеем
– новая неизвестная функция. Тогда по
формуле для производной сложной функции
имеем
![]()
Получим уравнение
первого порядка относительно ![]()
![]()
2. Разделяя переменные и интегрируя, находим
![]()
т.е.
![]()
(знак минус мы
выбрали из начального условия ![]() ).
).
3. Из начальных
условий (обоих) имеем ![]() при
при ![]() .
Отсюда,
.
Отсюда, ![]() .
Учитывая, что в силу первого начального
условия
.
Учитывая, что в силу первого начального
условия ![]() и, следовательно,
и, следовательно, ![]() ,
получаем
,
получаем
![]()
4. Разделяя переменные и интегрируя, находим
![]()
5. Из начального
условия ![]() получим
получим ![]() .
Следовательно,
.
Следовательно,
![]()
(Знак минус мы
выбрали из начального условия ![]() .)
.)
Ответ. ![]()
Условия задач. Найти решения задач Коши для дифференциальных уравнений
1. ![]() Ответ:
Ответ:
2. ![]() Ответ:
Ответ: ![]()
12.23. Линейные уравнения с постоянными коэффициентами
Постановка задачи. Найти общее решение линейного дифференциального уравнения второго порядка с постоянными коэффициентами
![]()
где ![]() - многочлен степени
- многочлен степени ![]() ,
,
![]() - многочлен степени
- многочлен степени ![]() и
и ![]() - действительные числа.
- действительные числа.
Алгоритм решения.
Общее решение неоднородного линейного уравнения -го порядка имеет следующую структуру:
![]()
где ![]() – фундаментальная система решений и
– фундаментальная система решений и
![]() - общее решение соответствующего
однородного уравнения,
- общее решение соответствующего
однородного уравнения, ![]() - какое-нибудь частное решение неоднородного
уравнения.
- какое-нибудь частное решение неоднородного
уравнения.
1. Записываем соответствующее однородное уравнение
![]()
и ищем его решение
в виде ![]() ,
где
,
где ![]() - неизвестное число.
- неизвестное число.
Подставляя ![]() и
и ![]() в уравнение (91) и сокращая
в уравнение (91) и сокращая ![]() ,
получаем так называемое характеристическое
уравнение
,
получаем так называемое характеристическое
уравнение
![]()
2. Решаем
характеристическое уравнение. Обозначим
корни характеристического уравнения
![]() и
и ![]() .
Тогда фундаментальная система решений
и общее решение уравнения (91) записываются
в одном из следующих трех видов:
.
Тогда фундаментальная система решений
и общее решение уравнения (91) записываются
в одном из следующих трех видов:
а) если ![]() и
и ![]() вещественны и
вещественны и ![]() ,
то фундаментальная система решений –
это
,
то фундаментальная система решений –
это ![]() и общее решение имеет вид
и общее решение имеет вид
![]()
б) если ![]() и
и ![]() вещественны и
вещественны и ![]() ,
то фундаментальная система решений –
это
,
то фундаментальная система решений –
это ![]() и общее решение имеет вид
и общее решение имеет вид
![]()
в) если ![]() и
и ![]() комплексные, т.е.
комплексные, т.е. ![]() ,
то фундаментальная система решений –
это
,
то фундаментальная система решений –
это ![]() и общее решение имеет вид
и общее решение имеет вид
![]()
3. Ищем какое-либо частное решение неоднородного уравнения. Поскольку правая часть уравнения имеет вид
![]()
можно применить метод подбора частных решений:
если ![]() не является корнем характеристического
уравнения (92), то
не является корнем характеристического
уравнения (92), то
![]()
где ![]() и
и ![]() - многочлены степени
- многочлены степени ![]() с неопределенными коэффициентами;
с неопределенными коэффициентами;
если ![]() есть корень характеристического
уравнения (92) кратности
есть корень характеристического
уравнения (92) кратности ![]() ,
то
,
то
![]()
где ![]() и
и ![]() - многочлены степени
- многочлены степени ![]() с неопределенными коэффициентами.
с неопределенными коэффициентами.
4. Находим
неопределенные коэффициенты, подставляя
![]() в исходное уравнение.
в исходное уравнение.
Записываем ответ по формуле (90).
Замечание 15. Аналогично решаются линейные дифференциальные уравнения с постоянными коэффициентами любого порядка.
Пример 29. Найти общее решение линейного дифференциального уравнения
![]()
Решение.
1. Записываем соответствующее однородное уравнение
![]()
и ищем его решение
в виде ![]() ,
где
,
где ![]() - неизвестное число.
- неизвестное число.
Подставляя ![]() и
и ![]() в уравнение (95) и сокращая
в уравнение (95) и сокращая ![]() ,
получаем так называемое характеристическое
уравнение
,
получаем так называемое характеристическое
уравнение
![]()
2. Характеристическое
уравнение имеет два комплексно сопряженных
корня ![]() .
.
Имеем фундаментальную систему решений
![]()
и общее решение однородного уравнения (95)
![]()
3. Ищем какое-либо
частное решение неоднородного уравнения
(94). В нашем случае правая часть
неоднородного уравнения имеет вид (93)
с ![]() .
.
Так как
характеристическое уравнение имеем
комплексные корни ![]() кратности
кратности ![]() и
и ![]() ,
то частное решение ищем в виде
,
то частное решение ищем в виде
![]()
где ![]() - неизвестные числа (неопределенные
коэффициенты).
- неизвестные числа (неопределенные
коэффициенты).
4. Находим
неопределенные коэффициенты, дифференцируя
![]() два раза и подставляя в уравнение (94).
два раза и подставляя в уравнение (94).
Приравнивая
коэффициенты в обеих частях равенства
при ![]() ,
получим четыре уравнения
,
получим четыре уравнения
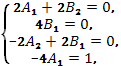
из которых определяем
![]() .
Таким образом,
.
Таким образом,
![]()
По формуле (90) находим общее решение неоднородного уравнения
![]()
Ответ. ![]()
Условия задач. Найти общие решения дифференциальных уравнений.
1. ![]() Ответ:
Ответ: ![]()
2. ![]() Ответ:
Ответ: ![]()
