Вопросы для зачета к математике для юристов.

1. Роль и место математики в современной науке и практике.

Математика является значительной и важной частью общечеловеческой культуры. Накопление математических фактов на протяжении тысячелетий развития человечества привело к возникновению математики как науки около двух с половиной тысяч лет тому назад. Обращаясь к истории философии, следует отметить, что ученые, создававшие математику, рассматривали ее как составную часть философии, которая служила средством познания мира. О значении математики для человечества говорит и тот факт, что книга Евклида "Начала" издавалась наибольшее число раз .

Математика уверен­но расположилась в самых разных частях и уголках современного мира. Что же дает людям математика, которая не открывает новых спосо­бов передвижения, как физика, и не создает новых вещей, как химия? Почему появление в какой-либо отрасли науки и техники математиче­ских методов означает и достижение в этой отрасли определенного уровня зрелости, и начало нового этапа ее дальнейшего развития?

          Наиболее распространенный ответ на эти вопросы еще не так давно состоял в том, что математика умеет хорошо вычислять и тем самым позволяет осуществлять математическую обработку цифровых данных, свя­занных с тем или иным изучаемым процессом. Однако при всей важности вычислительного аспекта математики, особенно в последние годы в связи с бурным ростом вычислительной техники, он оказывается неглавным при попытке объяснить причины математизации современного мира.

          Главная же причина этого процесса такова: математика предлагает весьма общие и достаточно четкие логические модели для изучения ок­ружающей действительности в отличие от менее общих и более рас­плывчатых моделей других наук. Объектами исследования математики служат логические модели, построенные для описания явлений в природе, технике, общест­ве. Математической моделью изучаемого объекта (явления, процесса и т.п.) называется логическая конструкция, отражающая геометрические формы этого объекта и количественные соотношения между его число­выми параметрами. При этом математическая модель, отображая и вос­производя те или иные стороны рассматриваемого объекта, способна замещать его так, что исследование модели даст новую информацию об этом объекте, опирающуюся на принципы математической теории, на сформулированные математическим языком законы природы. Если ма­тематическая модель верно отражает суть данного явления, то она позволяет находить и необнаруженные ранее закономерности, давать математический анализ условий, при которых возможно решение теоретических или практических задач, возникающих при исследовании этого явления. Такие модели формулируются на особом языке — языке чисел, различ­ных символов.

          Научное изложение должно быть ясным, точным, вполне определенным и кратким. Язык науки не должен создавать дополнительные трудности при восприятии сообщаемой информации, должен доносить идеи и факты в однозначном, не допускающем разночтения виде. Именно поэтому в науке должен применяться особый язык, максимально точно передающий присущие ей особенности. Кроме того, этот язык должен обладать свойством универсальности для применения в различных научных отраслях. Таким языком и является математика. Об этом было прекрасно сказано французским физиком-теоретиком начала XX века Луи де Бройлем: «…  где можно применить математический подход к проблемам, наука вынуждена пользоваться особым символическим языком, своего рода стенографией абстрактной мысли, формулы которой, когда они правильно записаны, по-видимому, не оставляют места ни для какой неопределенности, ни для какого неточного истолкования».

          Математическая символика не только не оставляет места для неточности  выражения мысли и расплывчатого толкования написанного, но вдобавок позволяет автоматизировать проведение тех действий, которые необходимы для получения выводов. Математическая символика выполняет и ряд других очень важных функций: сжимать запись информации, делать ее легко обозримой, удобной для последующей обработки и получения выводов. Обширные статистические сведения, собранные в результате эксперимента, удается посредством таблиц и  аналитических формул сжать до весьма короткой записи.

          По-видимому, впервые четко и ясно о математике как языке научного познания сказал великий итальянский естествоиспытатель Галилео Галилей: «Философия написана в величественной книге (я имею в виду Вселенную), которая постоянно открыта вашему взору, но понять ее может лишь тот, кто сначала научится понимать ее язык и толковать знаки, которыми она написана. Написана же она на языке математики, а знаки ее — треугольники, круги и другие геометрические фигуры, без которых человек не смог бы понять в ней ни слова, без них он был бы обречен блуждать в потемках по лабиринту». Позднее эта мысль повторялась многими знаменитыми учеными. Так, замечательный датский физик Нильс Бор заявил, что математика представляет собой значительно большее, чем просто наука, поскольку она является также языком науки.

          Итак, математика позволяет перевести «общежитейские», интуитивные подходы к действительности, базирующиеся на чисто качественных (а значит, приблизительных) описаниях, на язык точных определений и формул, из которых возможны количественные выводы. Не случайно говорят, что степень научности той или иной дисциплины измеряется тем, насколько в ней применяется математика. Широко известно высказывание Леонардо да Винчи, который по этому поводу писал: «Ни одно человеческое исследование не может называть­ся истинной наукой, если оно не прошло через математические доказательства».

          Владение математикой дает людям мощные методы изуче­ния и познания окружающего их мира, методы исследования как теоретических, так и практических проблем. Использование математического моделирования, дедуктивных методов и специального математического аппарата сближает гуманитарные и естественные науки. Одним из основных стимулов интеграции естественных и гуманитарных наук является математизация гуманитарных наук. Прежде в гуманитарных науках редко использовался де­дуктивный вывод (один из признаков научности), считавшийся у математиков единственно приводящим к «истинному» доказательству. Сегодня он используется в рамках многих гуманитарных наук. Наблюдается и обратное явление. В математику проникают подходы и мето­ды гуманитарных наук. Примером тому может являться теория нечетких множеств.

          Широкое проникновение математики и ее методов в другие отрасли знания является главнейшей формой взаимодействия наук, способствует сближению различных отраслей знания. Так, например, связь между физикой и химией очень часто осуществляется через математику. Математика изучает количественные закономерности, присущие всем предметам, явлениям действительности, и поэтому является необходимой всем областям знаний. Математика дает им мощный вычислительный аппарат, язык формул и т.д., без которых науки не могут развиваться успешно.

          На стыке математики и наук, где она применяется, возникают новые отрасли знания: математическая физика, математическая логика, математическая биология, математическая лингвистика, математическая психология и другие науки. Число таких отраслей знания в наше время постоянно растет.

          Одной из особенностей математизации знаний является ее универсальность, состоящая в том, что математические методы в наше время проникают во все сферы жизни людей. Люди в своей повседневной деятельности постоянно пользуются понятиями и выводами математики, нередко даже не задумываясь об этом. В современном производстве, в технике математика применяется особенно широко. Без всякого преувеличения можно сказать, что ни одно современное техническое усовершенствование невозможно без более или менее сложных математических расчетов.

          Связь математики с материальным производством можно обнаружить на всех этапах развития человечества. При этом чем шире и разнообразнее практическая деятельность людей, тем шире и разнообразнее требования к математике, тем необходимее становится ее применение. Связь математики с производственной деятельностью человека имеет тенденцию к усложнению, становится многоступенчатой. Например, в медицине применение широко математизированной науки – квантовой механики – позволяет описать химическое действие лечебных препаратов и их воздействие на человека. Здесь можно проследить сложную многоступенчатую связь математики с другими науками: математика – квантовая механика – химия – медицина.

         Таким образом, по мере усложнения задач, которые решает общество, возрастает роль математики.

2. Предмет математика. Основные этапы развития математики.

Название "математика" происходит от греческого слова "матейн" (mathein) - учиться, познавать. Древние греки вообще считали, что понятия "математика" (mathematike) и "наука", "познание" (mathema) - синонимы. Им было свойственно такое понимание универсализма этой отрасли знания, которое два тысячелетия спустя выразил Рене Декарт, писавший: "К области математики относят науки, в которых рассматриваются либо порядок, либо мера, и совершенно не существенно, будут ли это числа, фигуры, звезды, звуки или что-нибудь другое...; таким образом, должна существовать некая общая наука, объясняющая все, относящееся к порядку и мере, не входя в исследование никаких частных предметов..."

Математика в системе человеческих знаний есть раздел, занимающийся такими понятиями, как количество, структура, соотношение и т. п. Развитие математики началось с создания практических искусств счёта и измерения линий, поверхностей и объёмов.

Ясное понимание самостоятельного положения математики как особой науки, имеющей собственный предмет и метод, стало возможным только после накопления достаточно большого фактического материала и возникло впервые в Древней Греции в 6—5 веках до н. э. Развитие математики до этого времени естественно отнести к периоду зарождения математики, а к 6—5 веку до н. э. приурочить начало периода элементарной математики. В течение этих двух первых периодов математические исследования имеют дело почти исключительно с весьма ограниченным запасом основных понятий, возникших ещё на очень ранних ступенях исторического развития в связи с самыми простыми запросами хозяйственной жизни, сводившимися к счёту предметов, измерению количества продуктов, площадей земельных участков, определению размеров отдельных частей архитектурных сооружений, измерению времени, коммерческим расчётам, навигации и т. п. Первые задачи механики и физики [за исключением отдельных исследований греческого учёного Архимеда (3 век до н. э.), требовавших уже зачатков исчисления бесконечно малых] могли ещё удовлетворяться этим же запасом основных математических понятий. Единственной наукой, которая задолго до широкого развития математического изучения явлений природы в 17—18 веках систематически предъявляла математике свои особые и очень большие требования, была астрономия, целиком обусловившая, например, раннее развитие тригонометрии.

В 17 веке новые запросы естествознания и техники заставляют математиков сосредоточить своё внимание на создании методов, позволяющих математически изучать движение, процессы изменения величин, преобразования геометрических фигур (при проектировании и т. п.). С употребления переменных величин в аналитической геометрии французского учёного Декарта и создания дифференциального и интегрального исчисления начинается период математики переменных величин.

Дальнейшее расширение круга количественных отношений и пространственных форм, изучаемых математикой, привело в начале 19 века к необходимости отнестись к процессу расширения предмета математических исследований сознательно, поставив перед собой задачу систематического изучения с достаточно общей точки зрения возможных типов количественных отношений и пространственных форм. Создание русским математиком Н. И. Лобачевским его "воображаемой геометрии", получившей впоследствии вполне реальные применения, было первым значительным шагом в этом направлении. Развитие подобного рода исследований внесло в строение математики столь важные новые черты, что математика в 19 и 20 веках естественно отнести к особому периоду современной математики.

3. Аксиоматический метод построения научной теории.

Аксиоматический Метод   - способ построения научной те­ории, при котором какие-то положения теории избираются в каче­стве исходных, а все остальные ее положения выводятся из них чисто логическим путем, посредством доказательств. Положения, доказываемые на основе аксиом, называются теоремами. Аксиоматический метод — особый способ определения объектов и отношений меж­ду ними (см.: Аксиоматическое определение). Аксиоматический метод используется в математике, логике, а также в отдельных разделах физики, биологии и др.

Аксиоматический метод зародился еще в античности и приобрел большую извес­тность благодаря «Началам» Евклида, появившимся около 330 — 320 гг. до н. э. Евклиду не удалось, однако, описать в его «аксио­мах и постулатах» все свойства геометрических объектов, исполь­зуемые им в действительности; его доказательства сопровожда­лись многочисленными чертежами. «Скрытые» допущения гео­метрии Евклида были выявлены только в новейшее время Д. Гиль­бертом (1862-1943), рассматривавшим аксиоматическую теорию как формальную теорию, устанавливающую соотношения между ее элементами (знаками) и описывающую любые множества объек­тов, удовлетворяющих ей. Сейчас аксиоматические теории нередко формулируются как формализованные системы, содержа­щие точное описание логических средств вывода теорем из акси­ом. Доказательство в такой теории представляет собой последова­тельность формул, каждая из которых либо является аксиомой, либо получается из предыдущих формул последовательности по одному из принятых правил вывода. К аксиоматической формальной системе предъявляются тре­бования непротиворечивости, полноты, независимости системы ак­сиом и т. д. Аксиоматический метод является лишь одним из методов построения научного зна­ния. Он имеет ограниченное применение, поскольку требует высо­кого уровня развития аксиоматизируемой содержательной теории. Как показал известный математик и логик К. Гёдель, достаточ­но богатые научные теории (напр., арифметика натуральных чи­сел) не допускают полной аксиоматизации. Это свидетельствует об ограниченности аксиоматического метода и невозможности полной формализации научного знания (см.: Гёделя теорема)

(Аксиоматический метод – доказательство с помощью аксиом)

4. Геометрия Евклида. Неевклидовы геометрии.

Геометрия, как и другие науки, возникла из потребностей практики. Само слово «геометрия» греческое, в переводе означает «землемерие». Люди очень рано столкнулись с необходимостью измерять земельные участки. Это требовало определенного запаса геометрических и арифметических знаний. Постепенно люди начали измерять и изучать свойства более сложных геометрических фигур.

Наиболее совершенным образцом геометрии на протяжении более 2 тысяч лет служили «Начала» Евклида, написанные около 300 года до нашей эры. Евклид основывает математическую школу и пишет большой труд по геометрии, объединенных под общим названием «Начала» — главный труд своей жизни. Полагают, что он был написан около 325 года до нашей эры.  Каждая из книг начинается определением понятий (точка, линия, плоскость, фигура и т. д.), которые в ней используются, а затем на основе небольшого числа основных положений (5 аксиом и 5 постулатов), принимаемых без доказательства, строится вся система геометрии.

«Начала» Евклида представляют собой изложение той геометрии, которая известна и поныне под названием Евклидовой геометрии. В качестве постулатов Евклид выбрал такие предложения, в которых утверждалось то, что можно проверить простейшими построениями с помощью циркуля и линейки. Евклид принял также некоторые общие предложения-аксиомы, например, что две величины, порознь равные третьей, равны между собой. На основе таких постулатов и аксиом Евклид строго и систематично развил всю планиметрию.

В «Началах» он описывает метрические свойства пространства, которое современная наука называет Евклидовым пространством. Учение о параллельных и знаменитый пятый постулат («Если прямая, падающая на две прямые, образует внутренние и по одну сторону углы меньшие двух прямых, то продолженные неограниченно эти две прямые встретятся с той стороны, где углы меньше двух прямых») определяют свойства Евклидова пространства и его геометрию, отличную от неевклидовых геометрий.

Можно смело утверждать, что Евклид заложил основы не только геометрии, но и всей античной математики. Лишь в девятнадцатом веке исследования основ геометрии поднялись на новую, более высокую ступень. Удалось выяснить, что Евклид перечислил далеко не все аксиомы, которые на самом деле нужны для построения геометрии. В действительности при доказательствах ученый ими пользовался, но не сформулировал.

Неевклидова геометрия — в буквальном понимании — любая геометрическая система, отличная от геометрии Евклида; однако традиционно термин «неевклидова геометрия» применяется в более узком смысле и относится только к двум геометрическим системам: геометрии Лобачевского и сферической геометрии.

Как и евклидова, эти геометрии относятся к метрическим геометриям пространства постоянной кривизны. Нулевая кривизна соответствует евклидовой геометрии, положительная — сферической, отрицательная — геометрии Лобачевского.

Многовековые попытки доказательства пятого постулата Евклида привели в конце концов к появлению новой геометрии, отличающейся от евклидовой тем, что в ней V постулат не выполняется. Эта геометрия теперь называется неевклидовой, а в России носит имя Лобачевского, который впервые опубликовал работу с ее изложением.

Первые попытки Лобачевского доказать пятый постулат относятся к 1823 году. К 1826 году он пришел к убеждению в том, что V постулат не зависит от остальных аксиом геометрии Евклида и в 1826 году сделал на заседании факультета казанского университета доклад “Сжатое изложение начал геометрии со строгим доказательством теоремы о параллельных”, в котором были изложены начала открытой им “воображаемой геометрии”, как он называл систему, позднее получившую название неевклидовой геометрии. Доклад 1826г. вошел в состав первой публикации Лобачевского по неевклидовой геометрии.

5. Понятие множеств. Диаграммы Эйлера-Венна.

Понятие множества принадлежит к числу основных, неопределяемых понятий математики. Оно не сводится к другим, более простым понятиям. Поэтому его нельзя определить, а можно лишь пояснить, указывая синонимы слова «множество» и приводя примеры множеств: множество – набор, совокупность, собрание каких-либо объектов (элементов), обладающих общим для всех их характеристическим свойством.

Примеры множеств:

множество студентов в данной аудитории;

множество людей, живущих на нашей планете в данный момент времени;

множество точек данной геометрической фигуры;

множество чётных чисел;

множество корней уравнения х2-5х+6=0;

множество действительных корней уравнения х2+9=0;

Основоположник теории множеств немецкий математик Георг Кантор (1845-1918) писал: «Множество есть многое, мыслимое нами как единое». И хотя это высказывание учёного не является в полном смысле логическим определением понятия множества, но оно верно поясняет, что когда говорят о множестве, то имеют в виду некоторое собрание объектов, причём само это собрание рассматривается как единое целое, как один (новый) объект.

Объекты, составляющие данное множество, называют его элементами.

В математике часто исследуются так называемые числовые множества, т.е. множества, элементами которых являются числа. Для самых основных числовых множеств утвердились следующие обозначения:

N- множество всех натуральных чисел;

Z- множество всех целых чисел;

Q- множество всех рациональных чисел;

R- множество всех действительных чисел.

Диаграммы Эйлера-Венна

Для наглядного представления множеств используют диаграммы Эйлера-Венна. В этом случае множества обозначают областями на плоскости и внутри этих областей условно располагают элементы множества. Часто все множества на диаграмме размещают внутри прямоугольника, который представляет собой универсальное множество U. Если элемент принадлежит более чем одному множеству, то области, отвечающие таким множествам, должны перекрываться, чтобы общий элемент мог одновременно находиться в соответствующих областях. Выбор формы областей, изображающих множества на диаграммах, может быть произвольным (круги, внутренности эллипсов, многоугольники и т.п.).

Геометрически множества обычно изображаются как некоторые множества точек плоскости. В любой имеющей смысл задаче обычно рассматриваются подмножества некоторого "наибольшего" множества U, которое называют универсальным множеством. Так, на рис. изображено универсальное множество U и два его подмножества - множества А и В, B ⊂ A. Сами картинки типа данного рисунка называются диаграммами Эйлера-Венна.

6. Действия и свойства действий с множествами.

Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п.

Множества обозначаются заглавными латинскими буквами, а их элементы – строчными. Запись  a R  означает, что элемент  а  принадлежит множеству R , то есть  а  является элементом множества R . В противном случае, когда  а  не принадлежит множеству  R , пишут  a R .  

 

Два множества А и В называются  равными ( А = В ), если они состоят из одних и тех же элементов, то есть каждый элемент множества  А  является элементом множества  В  и наоборот, каждый элемент множества  В  является элементом множества  А .

 

Говорят, что множество А содержится в множестве В ( рис.1 ) или  множество А  является подмножеством множества  В ( в этом случае пишут А В ), если каждый элемент множества  А одновременно является элементом множества  В . Эта зависимость между множествами называется  включением. Для любого множества  А имеют место включения:  А  и  А  А .

Сумма ( объединение ) множеств  А и В ( пишется  А В ) есть множество элементов, каждый из которых принадлежит либо А , либо В. Таким образом,  е А В  тогда и только тогда, когда либо  е А ,  либо  е В .  

 

Произведение ( пересечение ) множеств  А и В ( пишется  А В , рис.2 ) есть множество элементов, каждый из которых принадлежит и А , и В . Таким образом,  е А В  тогда и только тогда, когда   е А  и  е В .

Разность множеств А и В ( пишется  А – В , рис.3 ) есть множество элементов, которые принадлежат множеству А , но не принадлежат множеству В. Это множество называется также дополнением множества В относительно множества А.

Симметричная разность множеств А и В ( пишется  А \ В  ) есть множество:

 

А \ В  = ( А – В ) ( В – А ).

 

 Свойства операций над множествами:

П р и м е р ы.  1. Множество детей является подмножеством всего населения.

 

                         2. Пересечением множества целых чисел с множеством поло-

                             жительных чисел является множество натуральных чисел.

 

 3. Объединением множества рациональных чисел с множест-

                             вом иррациональных чисел является множество действи-

                             тельных чисел.

 

                         4. Нуль является дополнением множества натуральных чисел

                             относительно множества неотрицательных целых чисел.

 

7. Элементы алгебры логики.

Алгебра логики — это математический аппарат, с помощью которого записывают, вычисляют, упрощают и преобразовывают логические высказывания.

   Создателем алгебры логики является живший в ХIХ веке английский математик Джордж Буль, в честь которого эта алгебра названа булевой алгеброй высказываний.

    Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.

     Употребляемые в обычной речи слова и словосочетания "не”, “и”, “или”, “если... , то”, “тогда и только тогда” и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.

    Высказывания, образованные из других высказываний с помощью логических связок, называются составными. Высказывания, не являющиеся составными, называются элементарными.

    Существуют три основные логические операции: отрицания (операция, выражаемая словом “не”), дизъюнкции (операция, выражаемая связкой “или”) и конъюнкции (операция, выражаемая связкой “и”).   Отрицание (инверсия) . Инверсия высказывания истина, когда само высказывание ложно, и ложно, когда высказывание истинно.

    Дизъюнкция (логическое сложение) двух или более высказываний ложно тогда и только тогда, когда все простые высказывания входящие в неё ложны.

    Конъюнкция(логическое умножение) двух или более высказываний истинно тогда и только тогда, когда все простые высказывания входящие в неё истины.

Существуют и другие логические операции.

   Операция, выражаемая связками “если ..., то”, “из ... следует”, “... влечет ...”, называется импликацией (лат. implico — тесно связаны) и обозначается знаком -->.

    Высказывание А-->  В ложно тогда и только тогда, когда А истинно, а В — ложно.     Операция, выражаемая связками “тогда и только тогда”, "необходимо и достаточно”, “... равносильно ...”, называется эквиваленцией или двойной импликацией и обозначается знаком  или <--> . Высказывание А  В истинно тогда и только тогда, когда значения А и В совпадают.

    Импликацию можно выразить через дизъюнкцию и отрицание:

    Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию:

    Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания (“не”), затем конъюнкция (“и”), после конъюнкции — дизъюнкция (“или”) и в последнюю очередь — импликация.

Логическая формула.

    С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой.

Определение логической формулы:

1. Всякая логическая переменная и символы “истина” (“1”) и “ложь” (“0”) — формулы.

2. Если А и В — формулы, то 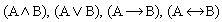 — формулы.

3. Никаких других формул в алгебре логики нет.

    Некоторые формулы принимают значение “истина” при любых значениях истинности входящих в них переменных. Такие формулы называются тождественно истинными формулами или тавтологиями.      Некоторые формулы принимают значение “ложно” при любых значениях истинности входящих в них переменных. Такие формулы называются тождественно ложными формулами или противоречиями. Если две формулы при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то они называются равносильными.

8. Основные логические операции.

Существуют три основные логические операции: отрицания (операция, выражаемая словом “не”), дизъюнкции (операция, выражаемая связкой “или”) и конъюнкции (операция, выражаемая связкой “и”).   Отрицание (инверсия) . Инверсия высказывания истина, когда само высказывание ложно, и ложно, когда высказывание истинно.

    Дизъюнкция (логическое сложение) двух или более высказываний ложно тогда и только тогда, когда все простые высказывания входящие в неё ложны.

    Конъюнкция(логическое умножение) двух или более высказываний истинно тогда и только тогда, когда все простые высказывания входящие в неё истины.

Существуют и другие логические операции.

   Операция, выражаемая связками “если ..., то”, “из ... следует”, “... влечет ...”, называется импликацией (лат. implico — тесно связаны) и обозначается знаком -->.

    Высказывание А-->  В ложно тогда и только тогда, когда А истинно, а В — ложно.     Операция, выражаемая связками “тогда и только тогда”, "необходимо и достаточно”, “... равносильно ...”, называется эквиваленцией или двойной импликацией и обозначается знаком  или <--> . Высказывание А  В истинно тогда и только тогда, когда значения А и В совпадают.

    Импликацию можно выразить через дизъюнкцию и отрицание:

    Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию:

    Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания (“не”), затем конъюнкция (“и”), после конъюнкции — дизъюнкция (“или”) и в последнюю очередь — импликация.

9. Составления таблиц истинности.

Таблица истинности – это таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний

Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы. Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре:

(0, 0),     (0, 1),     (1, 0),     (1, 1).

Если формула содержит три переменные, то возможных наборов значений переменных восемь:

(0, 0, 0),     (0, 0, 1),     (0, 1, 0),     (0, 1, 1),     (1, 0, 0),     (1, 0, 1),     (1, 1, 0),     (1, 1, 1).

Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д. Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.

Алгоритм построения таблицы истинности:

1. подсчитать количество переменных n в логическом выражении;

2. определить число строк в таблице m = 2n;

3. подсчитать количество логических операций в формуле;

4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;

5. определить количество столбцов в таблице: число переменных плюс число операций;

6. выписать наборы входных переменных ;

7. провести заполнение таблицы истинности по столбикам, выполняя логические операции в соответствии с установленной в п.4 последовательностью

Наборы входных переменных, рекомендуют перечислять следующим образом:

• определить количество наборов входных переменных;

• разделить колонку значений первой переменной пополам и заполнить верхнюю часть колонки 0, а нижнюю —1;

• разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами 0 или 1, начиная с группы 0;

• продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами 0 или 1 до тех пор, пока группы 0 и 1 не будут состоять из одного символа.

Приоритеты операций

1. операции в скобках ()

2. отрицание

3. конъюнкция

4. дизъюнкция

5. импликация

6. эквивалентность

ПОСТРОЕНИЕ ТАБЛИЦ ИСТИННОСТИ ДЛЯ СЛОЖНЫХ   ВЫСКАЗЫВАНИЙ

Истинность или ложность сложных суждений представляет собой функцию истинности или ложности простых. Эту функцию называют БУЛЕВОЙ ФУНКЦИЕЙ СУЖДЕНИЙ (F(A,B)). Рассмотрим примеры построения таблиц истинности для сложных суждений.

1. ¬¬А <=> А (закон "отрицания отрицания": Отрицание отрицания суждения тождественно самому суждению.)

А	¬А	¬¬А	¬¬A<=>A
И	Л	И	И
Л	И	Л	И

Если значение истинности булевой функции всегда истина, то эта функция выражает ЗАКОН.

2. ((А => В) & ¬В) => ‾A (доказательство "от противного": Если А влечет В, но В не верно, то не верно и А.)

A	B	A=>B	¬B	(A=>B)&¬B	¬A	((A=>B)&¬B)=>¬A
И И Л Л	И Л И Л	И Л И И	Л И Л И	Л Л Л И	Л Л И И	И И И И

Пример:

1. Для формулы A /\ (B \/ ¬ B/\¬ C) построить таблицу истинности.

Количество логических переменных 3, следовательно, количество строк в таблице истинности должно быть 23 = 8. Количество логических операций в формуле 5, следовательно количество столбцов в таблице истинности должно быть 3 + 5 = 8.

A	B	C	¬ B	¬ C	¬ B/\¬ C	B \/( ¬¬C) B/\	A/\ (B \/¬ B/\¬ C)
0	0	0	1	1	1	1	0
0	0	1	1	0	0	0	0
0	1	0	0	1	0	1	0
0	1	1	0	0	0	1	0
1	0	0	1	1	1	1	1
1	0	1	1	0	0	0	0
1	1	0	0	1	0	1	1
1	1	1	0	0	0	1	1

2.  Составим таблицу истинности для формулы , которая содержит две переменные x и y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим таблицу:

Переменные			Промежуточные логические формулы						Формула
0	0	1		0	0	1	1	1
0	1	1		1	1	0	1	1
1	0	0		0	1	0	0	1
1	1	0		0	1	0	0	1

Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 1, то есть является тождественно истинной.

3. Таблица истинности для формулы :

Переменные		Промежуточные логические формулы					Формула
0	0	0	1	1	0	0
0	1	1	0	0	0	0
1	0	1	0	1	1	0
1	1	1	0	0	0	0

Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 0, то есть является тождественно ложной.

4. Таблица истинности для формулы :

Переменные			Промежуточные логические формулы						Формула
0	0	0	1	1	0	1	0	0
0	0	1	1	1	0	1	1	1
0	1	0	0	0	1	1	0	1
0	1	1	0	0	1	1	1	1
1	0	0	1	1	0	0	0	0
1	0	1	1	1	0	0	0	0
1	1	0	0	1	0	0	0	0
1	1	1	0	1	0	0	0	0

Из таблицы видно, что формула в некоторых случаях принимает значение 1, а в некоторых — 0, то есть является выполнимой.

10. Основные элементы к комбинаторике. Правила комбинаторики; выборки элементов.

Комбинаторика - это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиально возможное количество различных вариантов развития событий.

Основные понятия комбинаторики. Комбинаторика изучает количество комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества. При непосредственном вычислении вероятностей часто используются формулы комбинаторики. Приведем наиболее употребительные из них. 1.Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающимися только порядком их расположения. Число всех возможных перестановок Pn = n!, где n! = 1?2?3 ? n, 0! = 1. Пример 1. Сколько трехзначных чисел можно составить из цифр 1,2,3, если каждая цифра входит в изображение числа только один раз? Решение. P3 = 3! = 1?2?3 = 6. 2.Размешениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. An m =n!/(n-m)! Пример 2. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2? Решение . A 2 6 = 6! ?(6-2)! = 720 / 24 = 30. 3.Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хоты бы одним элементом. Cnm = n!/(m!(n-m)!). Пример 3. Скольким количеством способов можно выбрать две детали из ящика, содержащего 10 деталей? Решение. C21 0 =10!/(2! ?8!) = 45. Подчеркнем что числа размещений, перестановок и сочетаний связаны равенством. Anm = PmCnm Основные правила комбинаторики

Большинство комбинаторных задач решается с помощью двух основных правил - правила суммы и правила произведения.

4.2. Правило суммы, правило произведения. Правило суммы. Если некоторые объект А может быть выбран из совокупности объектов m способами, а другой объект В можно выбрать n способами. То выбрать либо А, либо В можно m + n способами. Правило произведения. Если некоторые объект А может быть выбран из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указном порядке может быть выбрана m ? n способами.

Правило суммы. Если некоторый объект можно выбрать способами, а другой объект можно выбрать способами, то выбор "либо , либо " можно осуществить способами.

Правило произведения. Если объект можно выбрать способами, а после каждого такого выбора другой объект можно выбрать (независимо от выбора объекта способами, то пары объектов и можно выбрать способами.

11. Выборки элементов (без повторения и с повторениями).

Основные правила комбинаторики

Большинство комбинаторных задач решается с помощью двух основных правил - правила суммы и правила произведения.

Правило суммы. Если некоторый объект можно выбрать способами, а другой объект можно выбрать способами, то выбор "либо , либо " можно осуществить способами.

Правило произведения. Если объект можно выбрать способами, а после каждого такого выбора другой объект можно выбрать (независимо от выбора объекта способами, то пары объектов и можно выбрать способами.

Пусть = {, , ..., }, = {, , ..., } и А - число элементов множества . Составим декартово произведение множеств и , т.е. множество пар (, .

Тогда правило произведения записывается следующим образом:

Пример 6. Сколько существует двузначных чисел?

Решение. Поскольку в двузначном числе цифра, обозначающая число десятков, должна быть отлична от нуля, то = {1, 2, ..., 9}, = {0, 1, 2, ..., 9} и