Министерство образования Российской Федерации

Омский государственный технический университет

Методические указания

И

Типовой расчет по аналитической геометрии Для студентов-заочников 1 курса

Омск – 2002

Составители: Назарук Елена Маратовна, преподаватель,

Ананко Алла Александровна, ассистент

Тема 1. Прямая на плоскости

Уравнение любой прямой , лежащей в плоскости XOY, является уравнением первой степени относительно текущих координат x , y и имеет вид

. (1)

Уравнение (1) называется общим уравнением прямой.

Если свободный член С равен нулю, то уравнение прямой имеет вид , ему удовлетворяют координаты точки О(0; 0), а прямая проходит через начало координат. Если коэффициент А=0, то уравнение принимает вид . Его можно переписать в виде , и эта прямая проходит через точку параллельно оси ОХ. Если коэффициент В = 0, то уравнение прини-мает вид Ах + С = 0. Его можно переписать в виде , и эта прямая проходит через точку параллельно оси OY.

Из общего уравнения прямой (1) можно получить уравнение прямой в отрезках.

Перенесем слагаемое С в правую часть: . Разделим левую и правую часть уравнения на минус С: . Введем обозначения . Получим ­ – (2)

уравнение прямой в отрезках, где – отрезок, отсекаемый прямой на оси ОХ, – отрезок, отсекаемый прямой на оси OY (рис. 1).

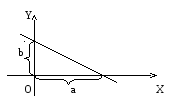
Рис. 1

Всякий ненулевой вектор , перпендикулярный прямой, назовем нор-мальным вектором этой прямой. Рассмотрим на плоскости XOY произвольную прямую (рис. 2).

Рис. 2

Пусть точка – некоторая фиксированная ее точка и – произвольная точка. Тогда координаты вектора: .

Так как то их скалярное произведение равно нулю Выражая скалярное произведение через координаты векторов, запишем

. (3)

Полученное уравнение является уравнением прямой, проходящей через точку перпендикулярно вектору .

Уравнение прямой, проходящей через точку , с данным угловым коэффициентом k (где – угол между прямой и положительным направ-лением оси OX) имеет вид . (4)

Всякий ненулевой вектор , параллельный данной прямой или лежащий на ней, назовем направляющим вектором этой прямой.

Рассмотрим на плоскости XOY произвольную прямую (рис. 3). Пусть точка – некоторая фиксированная ее точка, а – произвольная точка. Тогда координаты вектора . Так как векторы коллинеарны, то пропорциональны их соответствующие координаты:

(5)

Полученное уравнение называется каноническим уравнением прямой.

Y

M

M₁

X

Рис. 3

Уравнение прямой, проходящей через две данные точки и , выражается формулой

. (6)

Пусть прямая задана общим уравнением (1). Разрешим его относительно y.

Введем обозначения . Окончательно получаем . (7)

Это уравнение называется уравнением прямой с угловым коэффициентом k.

Условием параллельности двух прямых с угловыми коэффициентами соответственно является равенство этих угловых коэффициентов: .

Условие перпендикулярности двух прямых выражается равенством или .

Если две пересекающиеся прямые не перпендикулярны, то тангенс угла φ между ними находится по формуле

. (8)

Пусть даны две прямые с уравнениями и и требуется найти точку их пересечения. Так как эта точка принадлежит каждой прямой, ее координаты должны удовлетворять уравнению как первой прямой, так и второй. Таким образом, чтобы найти координаты точки пересечения двух прямых, следует решить систему уравнений

Пусть на плоскости XOY заданы прямая и точка . Расстояние от точки до прямой – это длина перпендикуляра, опущенного из точки М₁ на эту прямую. Это расстояние выражается формулой

. (9)

Задача 1. Даны координаты точек А(1; 2), В(2; 5), С(-3; 6). Найти:

а) уравнение стороны АС треугольника АВС;

б) уравнение высоты ВН, ее длину;

в) уравнения медиан СС₁, АА₁ треугольника АВС;

г) точку пересечения медиан СС₁, АА₁;

д) угол А треугольника АВС;

е) уравнения сторон AD, CD параллелограмма ABCD;

ж) координаты вершины D параллелограмма ABCD.

Решение.

а) Воспользуемся уравнением прямой (5), проходящей через две точки, где – координаты точки А, – координаты точки С.

,

Ответ: Уравнение стороны АС: .

б) Найдем координаты вектора по формулам , . Так как высота ВН перпендикулярна вектору , он будет являться нормальным вектором этой прямой. Составим уравнение высоты, используя уравнение прямой, проходящей через данную точку В(2; 5) перпендикулярно вектору нормали , где А=-4; В=4:

Длину высоты найдем, используя формулу (9), как расстояние от точки В до прямой АС (уравнение АС найдено в п. а)):

Ответ: Уравнение высоты ВН: x-y+3=0, ее длина .

в) Найдем координаты точки С₁ – середины отрезка АВ:

.

.

Уравнение медианы СС₁ составим, используя уравнение прямой, проходящей через две точки (5):

Уравнение медианы АА₁ находится аналогично:

.

Ответ: Уравнение медианы СС₁: 5х+9у-39=0,

уравнение медианы АА₁: 7х+3у-13=0.

г) Точку пересечения медиан АА₁ и СС₁ найдем, решив систему их уравнений:

-16х = 0,

.

Ответ: точка пересечения медиан

д) Найдем уравнение стороны АВ, используя формулу (6)

.

Выразим отсюда y и найдем k₁ – угловой коэффициент стороны АВ:

Уравнение стороны АС найдено в пункте а) :.

Выразим у и найдем k₂ – угловой коэффициент стороны АС:

Угол А найдем по формуле (7) как угол между прямой АВ и АС:

Ответ: Угол

е) Так как в параллелограмме противоположные стороны параллельны, используем уравнение прямой (5)

.

Найдем координаты вектора : . Координаты точки А(1;2), т.е. . Следовательно, уравнение стороны AD:

.

Аналогично находится уравнение стороны CD: , :

Ответ: AD:

ж) Координаты четвертой вершины D параллелограмма ABCD найдем как точку пересечения прямых AD и CD. Решим систему

Ответ: D(-4; 3).