13.3. Действительные числа.
В школьном курсе математики изучаются действительные (вещественные) числа.
Сначала из потребностей счета возникает натуральный ряд чисел N = {1, 2, 3, …, n, …}, его члены называются натуральными числами. В множестве натуральных чисел определен строгий порядок: из двух натуральных чисел то, которое в натуральном ряде появляется раньше, называется меньшим, второе число – большим. В множестве натуральных чисел определены две операции: сложение и умножение натуральных чисел.
Однако операции вычитания и деления не всегда выполнимы в множестве натуральных чисел N. Поэтому расширение понятия числа пошло в двух направлениях. Возникают отрицательные числа и число ноль, т.е. возникает множество целых чисел Z = {0, ±1, ±2, …, ±n,…}.
Необходимость
рассмотрения частей целого приводит к
появлению долей единицы и дробных чисел
,
где m,
nN.
В итоге этих расширений понятия числа
возникает множество
рациональных чисел
Q={
:
mZ,
nN}.
Это множество обладает, в отличие от множеств N и Z, тем свойством, что оно замкнуто относительно арифметических операций сложения и вычитания, умножения и деления: сумма и разность, произведение и частное двух рациональных чисел снова является рациональным числом. Всякое рациональное число единственным образом может быть представлено как бесконечная десятичная периодическая дробь.
С другой стороны, извлечение корня любой степени не всегда возможно в области рациональных чисел, в частности, нет рационального числа, квадрат которого равен 2. этот недостаток рациональных чисел восполняют иррациональные числа, т.е. бесконечные десятичные непериодические дроби, например
=
1,414213562…; π = 3,141592654; е
= 2,718281828… .
Иррациональные
числа нельзя представить в виде отношения
,
где mZ,
nN.
Рациональные и иррациональные числа (бесконечные десятичные периодические и непериодические дроби) образуют множество действительных чисел R; при этом
N Z Q R.
На действительные числа переносятся действия сложения и вычитания, умножения и деления, возведения в степень и извлечение корня n-ой степени, nN, из положительного числа и т.д., в частности, отношение порядка: про любые два действительные числа можно сказать, какое из них больше, а какое меньше.
Геометрически действительные числа изображаются точками числовой оси или координатной прямой (т.н. процесс десятичного измерения отрезка прямой).
Рассмотрим прямую с выбранным на ней направлением, начальной точкой О и единичным отрезком ОЕ (см. рис. 13.2). С помощью отрезка ОЕ можно измерить длину любого отрезка, например, отрезка ОА.
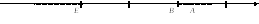
О
Отрезок ОЕ укладывается в отрезке ОА три раза (это целая часть числа). Разделим единичный отрезок ОЕ на 10 равных частей и отложим десятую часть отрезка ОЕ в остатке ВА два раза. Тогда число 3,2 есть приближенное значения длины отрезка ОА с точностью до 0,1. Продолжая этот процесс, мы получим десятичную дробь, выражающую длину отрезка ОА. Полученная десятичная дробь есть действительное число, а точка А изображает число на числовой оси. Числовая ось есть не что иное, как линейка.
В современной математике принят аксиоматический теоретико-множественный подход к понятию действительного числа. Дадим основное определение.
Множество R называется множеством действительных чисел, если оно удовлетворяет следующим условиям (аксиомам):
(I). Операция сложения.
Для каждых двух чисел xR и уR определено число х+уR, называемое их суммой, при этом выполняются аксиомы сложения:
1+ (х+у)+z=x+(y+z),
2+ x+y=y+x,
3+
число ноль, 0R,
такое, что
хR (x+0=0+x=x),
4+
хÎR
противоположное (–х)R,
такое, что х+(–х)=(–х)+х
=0.
(II). Операции умножения.
Для каждых двух чисел xR и уR определено число х•уR, называемое их произведением, при этом выполняются аксиомы умножения:
1 (х•у)•z=x•(y•z),
2´ x•y=y•x,
3´
число 1R,
1≠0, называемое единицей,
такое, что 
хÎR
1•х =
х•1=х,
4´
хÎR,
х≠0,
обратное
число х
-1ÎR
такое, что х•
х -1=
х -1•х=1
(I, II). Связь сложения и умножения.
(Дистрибутивность умножения по отношению к сложению)
(х+у)z = xz+yz
(III). Отношение порядка.
На множестве R определено отношение неравенства ≤, при этом выполняются аксиомы неравенства:
1≤
х≤х
хÎR
(рефлексивность);
2≤
(х≤у)
(y≤x)
=> (x=y),
(антисимметричность);
3≤
(х≤у)
(y≤z)
=> (x≤z),
(транзитивность);
4≤ Для каждых двух чисел xR и уR выполняется одно из двух условий:
(х≤у)
(y≤x).
(I, III). Связь сложения и порядка.
(х≤у) => (x+z ≤ y+z).
(II, III). Связь умножения и порядка.
(0≤х)
(0≤y)
=> (0≤xy).
(IV). Полнота (непрерывность) действительных чисел
Если
Х
и Y-
непустые подмножества множества R,
т.е. ХR,
X≠Ø,
YR,
Y≠Ø,
и
хÎX
yÎY
x≤y.
Тогда
найдется число сR
такое, что
хÎX
yÎY
x ≤ с ≤ y.
В теории множеств доказывается, что вышеприведенные аксиомы однозначно определяют объект, называемый множеством действительных чисел, и что ранее построенное множество R есть конкретная реализация аксиоматики действительных чисел.
Некоторые следствия из аксиом:
-
Разность чисел. По определению: а–b=a+(-b);
-
Обратный элемент. По определению: а-1=
; -
х•0=0
хÎR;
(х
у=0)
=> (х =
0)
(у
= 0).
-
Строгое неравенство. По определению
(х<y)
(x≤y)
(x≠y).
Для каждых двух чисел хR и yR выполняется только одно из неравенств:
х < y, x = y, x > y
В
частности, 0<1 и х>y>0
=>
<
.
-
Принцип Архимеда:
аÎR
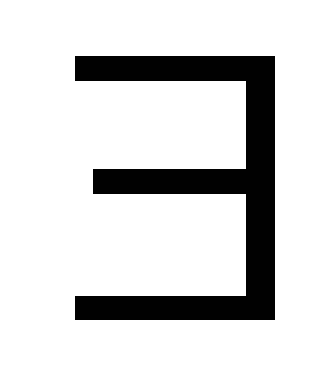nÎN:
n>a.
-
а>0
b>0
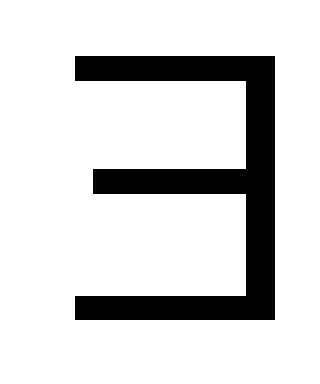nÎN:
na>b, -
ε>0
nÎN:
0<
<ε, -
если 0≤х<
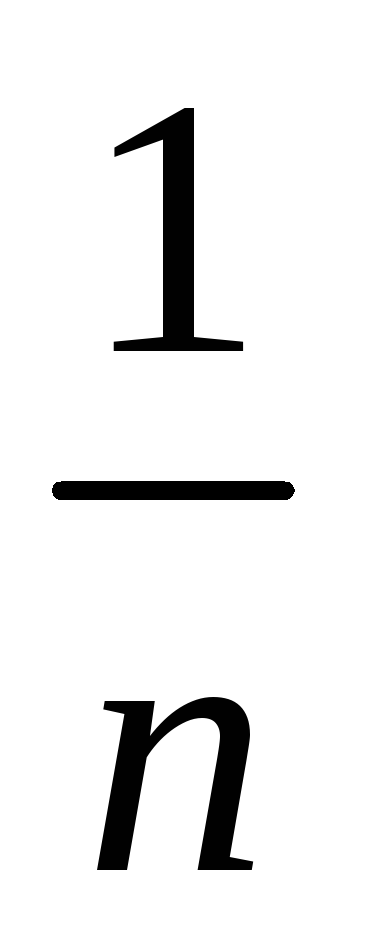
nÎN,
то х=0.
-
Абсолютная величина числа: |х| =
.
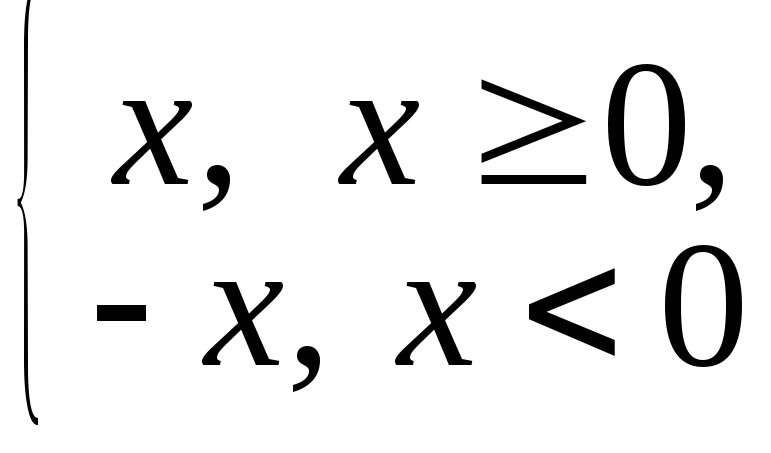Некоторые ее свойства:
|а|0,
|а+b|≤|a|+|b|,
|ab|=|a|•|b|,
.
Второе неравенство называется неравенством треугольника.
Расстояние между числами: (х, у) = |х–у|.