- •Федеральное агентство по образованию
- •Алгебра и аналитическая геометрия. Математический анализ
- •305040 Курск, ул. 50 лет Октября, 94. Содержание
- •Введение
- •1.Контрольные задания
- •2. Указания к решению типового варианта
- •2.1. Пример выполнения задания 1
- •2.2. Пример выполнения задания 2
- •2.3. Указания к заданию 3
- •2.3.1. Основные теоретические положения
- •Первый замечательный предел
- •Второй замечательный предел
- •Некоторые типы пределов
- •2.3.2. Пример выполнения задания 3
- •2.4. Указания к заданию 4
- •2.4.1. Основные теоретические положения
- •2.4.2.Пример выполнения задания 4
- •2.5. Указания к заданию 5
- •2.5.1. Основные теоретические положения
- •Производные функций, заданных параметрически
- •2.5.2. Пример выполнения задания 5
- •2.6. Пример выполнения задания 6
- •2.7. Пример выполнения задания 7
- •Список рекомендуемой литературы
2.3. Указания к заданию 3
2.3.1. Основные теоретические положения
При вычислении пределов необходимо помнить их свойства:
если существуют
конечные
![]()
![]() ,
то
,
то
1.
![]()
т.е. предел суммы двух функций равен сумме пределов этих функций.
Замечание:
Если
![]() ,
то это свойство не верно и имеем
неопределенность
,
то это свойство не верно и имеем
неопределенность
![]() .
.
2.
![]()
т.е. предел произведения двух функций равен произведению пределов этих функций.
Замечание:
Если
![]() ,
то это свойство не верно и имеем
неопределенность
,
то это свойство не верно и имеем
неопределенность
![]() .
.
Если
![]() где
где
![]() то
то
![]()
т.е. постоянный множитель можно выносить за знак предела.
3.
![]()
т.е. предел частного двух функций есть частное пределов этих функций.
Замечание:
Если
![]() или А=0, В=0, то это свойство не верно и
имеем неопределенность
или А=0, В=0, то это свойство не верно и
имеем неопределенность
![]() или
или
![]() .
.
4.
![]() .
.
Замечание:
Если
![]() ,
или
,
или
![]() ,
или
,
или
![]()
![]() ,
то это свойство не верно и имеем
неопределенность
,
то это свойство не верно и имеем
неопределенность
![]() ,
или
,
или
![]() или
или
![]() .
.
Первый замечательный предел
![]() ,
неопределенность
,
неопределенность
![]() .
.
Следствия:
1.
![]() ,
2.
,
2.
![]() ,
,
3.
![]() ,
4.
,
4.
![]() ,
,
5.![]() ,
6.
,
6.
![]()
7.
![]() .
.
Второй замечательный предел
![]() ,
неопределенность
,
неопределенность
![]() ,
,
![]() .
.
Следствия:
1.
![]() ,
2.
,
2.
![]() ,
,
3.
![]() ,
4.
,
4.
![]() ,
,
5.
![]() ,
6.
,
6.
![]() .
.
Некоторые типы пределов
При вычислении
предела вида
![]() можно выделить три случая:
можно выделить три случая:
1 случай: степень многочлена числителя меньше степени многочлена знаменателя (n < m), то такой предел равен 0;
2 случай: степень многочлена числителя больше степени многочлена знаменателя (n > m), то такой предел равен ;
3 случай: степени многочленов числителя и знаменателя равны (n=m), то такой предел равен отношению коэффициентов при старших степенях.
2.3.2. Пример выполнения задания 3
а)
![]() .
.
Подставляя вместо
переменной
![]() ,
получим неопределенность вида
,
получим неопределенность вида
![]() ,
которая легко раскрывается, если и
численность и знаменатель разложить
на множители. Для разложения числителя
найдем корни уравнения
,
которая легко раскрывается, если и
численность и знаменатель разложить
на множители. Для разложения числителя
найдем корни уравнения
![]()
![]() ,
,
![]()
Используя формулу
![]() получаем
получаем
![]() Выражение
Выражение
![]() раскладывается как разность кубов, т.е.
раскладывается как разность кубов, т.е.
![]() .
Таким образом, получим
.
Таким образом, получим
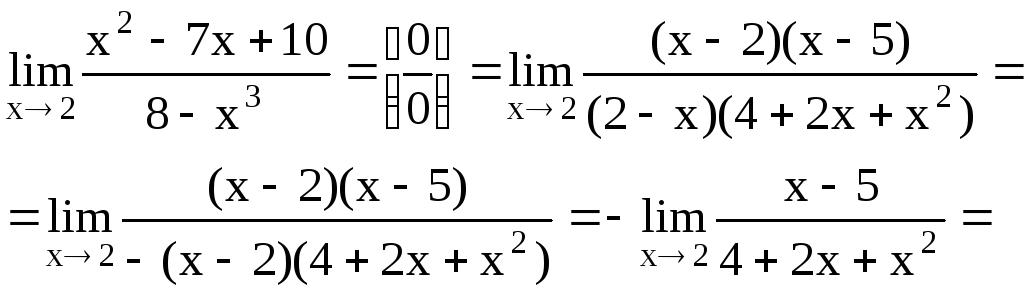
![]()
б)
![]() .
.
Имеем
неопределенность вида
![]() .
Чтобы ее раскрыть, вынесем и в числители
и в знаменателе переменную в большей
степени, т.е.
.
Чтобы ее раскрыть, вынесем и в числители
и в знаменателе переменную в большей
степени, т.е.
![]() ,
за скобку, получим
,
за скобку, получим
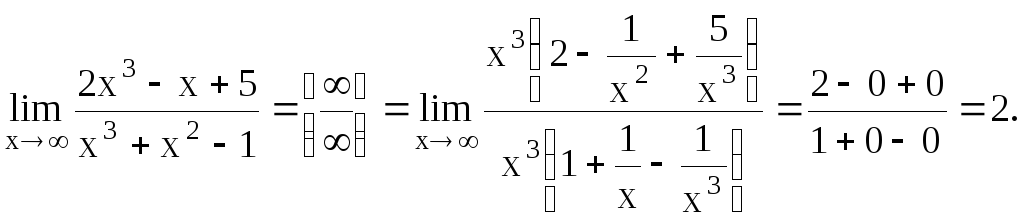
в)
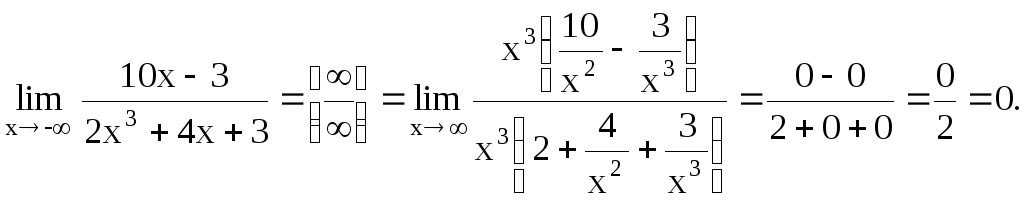
г)
![]()
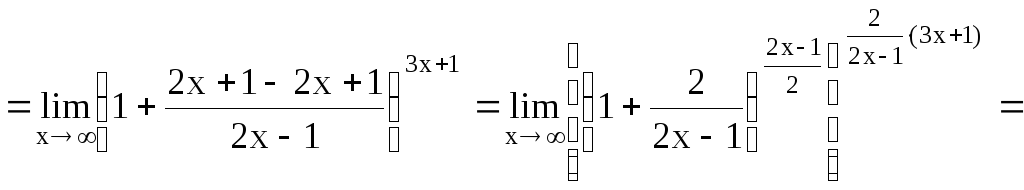
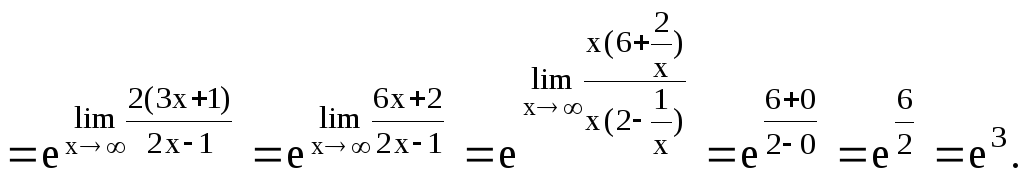
д)
![]()
е)
![]()
![]()
2.4. Указания к заданию 4
2.4.1. Основные теоретические положения
Для непрерывности
функции f(x)
в точке
![]() необходимо и достаточно выполнение
условий:
необходимо и достаточно выполнение
условий:
-
функция f(x) должна быть определена в точке
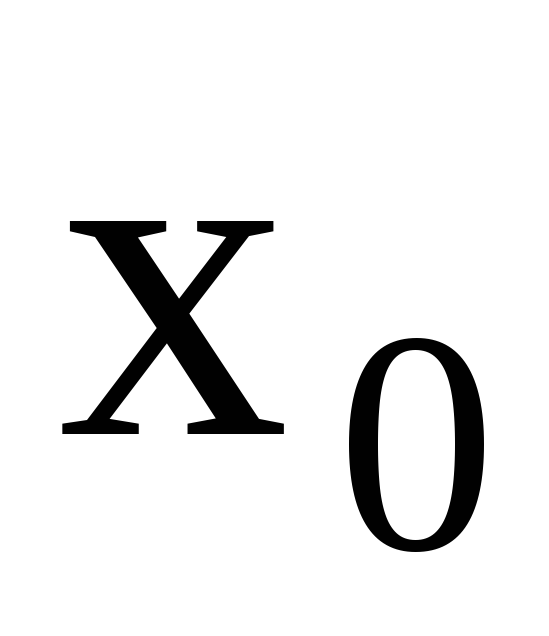 ,
т.е. можно вычислить значение
,
т.е. можно вычислить значение
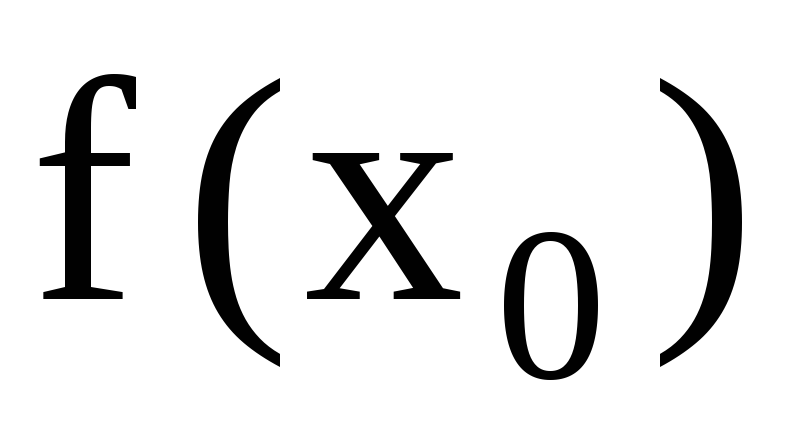 ;
; -
должны существовать и быть конечными односторонние пределы
![]()
-
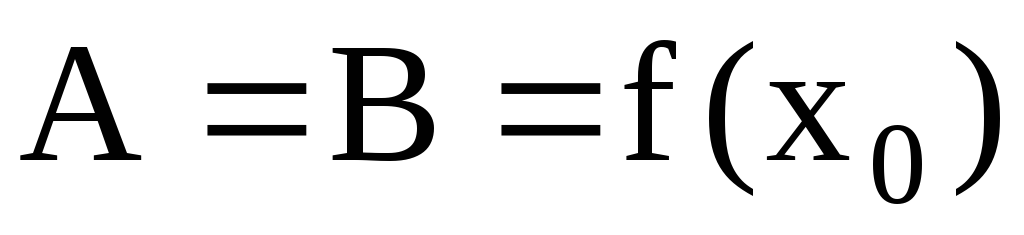 .
.
Если все эти три
условия выполнены, то
![]()
точка непрерывности функции f(x).
точка непрерывности функции f(x).
Точки разрыва
функции можно разделить на устранимый
разрыв, точки разрыва первого и второго
рода. У точек разрыва первого рода
односторонние пределы должны существовать,
быть конечными, но не равными друг другу.
Если хотя бы один из односторонних
пределов не существует или равен ,
то
![]() есть точки разрыва второго рода.
есть точки разрыва второго рода.
2.4.2.Пример выполнения задания 4
Исследовать данную функцию на непрерывность и построить ее график
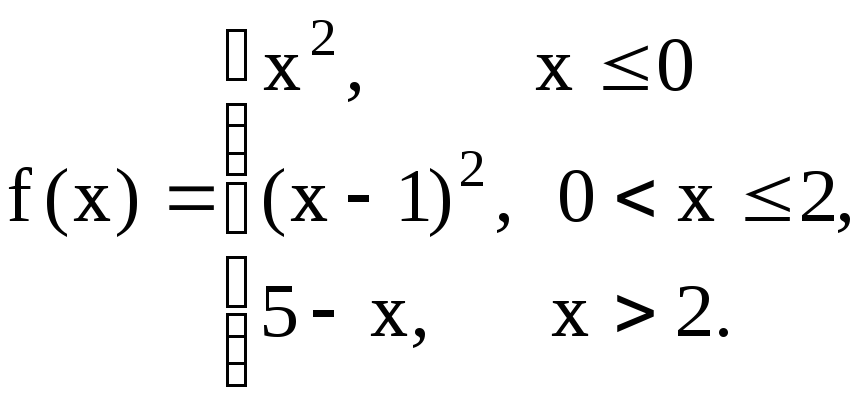
Решение.
Функция f(x)
определена и непрерывна на интервалах
![]() ,
где она задана непрерывными элементарными
функциями. Следовательно, разрыв возможен
только в точках
,
где она задана непрерывными элементарными
функциями. Следовательно, разрыв возможен
только в точках
![]() и
и
![]()
Для точки
![]() имеем:
имеем:
![]()
![]()
![]()
т.е. функция f(x)
в точке
![]() имеет разрыв первого рода.
имеет разрыв первого рода.
Для точки
![]() находим:
находим:
![]()
![]()
![]()
т.е. функция f(x)
в точке
![]() также имеет разрыв первого рода, т.к.
односторонние пределы конечны, но не
равны.
также имеет разрыв первого рода, т.к.
односторонние пределы конечны, но не
равны.
Построим график