Глава III Точные решения уравнений движения вязких (ньютоновских и неньютоновских) жидкостей
§1. Ламинарное прямолинейное установившееся движение вязких жидкостей в круглых трубах
Жидкость считаем
несжимаемой (
),
движение установившемся
.
Рассмотрим случай,
когда траектории всех частиц будут
строго прямолинейными и параллельными
между собой. Направим ось Oх
по оси трубы. Тогда
положим
равным
[10].
Из уравнения
неразрывности получим, что
,
то есть
.
Вследствие этих
предположений квадратичные члены
инерции выпадают из полных уравнений
движения. Из–за симметрии течения
относительно оси трубы
определяется не самими координатами y
и z,
а лишь их комбинацией
,
являющейся расстоянием точки сечения
трубы от оси, то есть
.
В общем случае одномерного течения ньютоновских и неньютоновских вязких жидкостей
(3.1)
где
Для вязкой ньютоновской жидкости
Для степенной жидкости
Для вязкопластичной жидкости
или
0
при
при
Распределение касательного напряжения по радиусу.
Выделим внутри жидкости, движущейся по трубе, цилиндр радиуса r и длиной l (рис. 3.1).
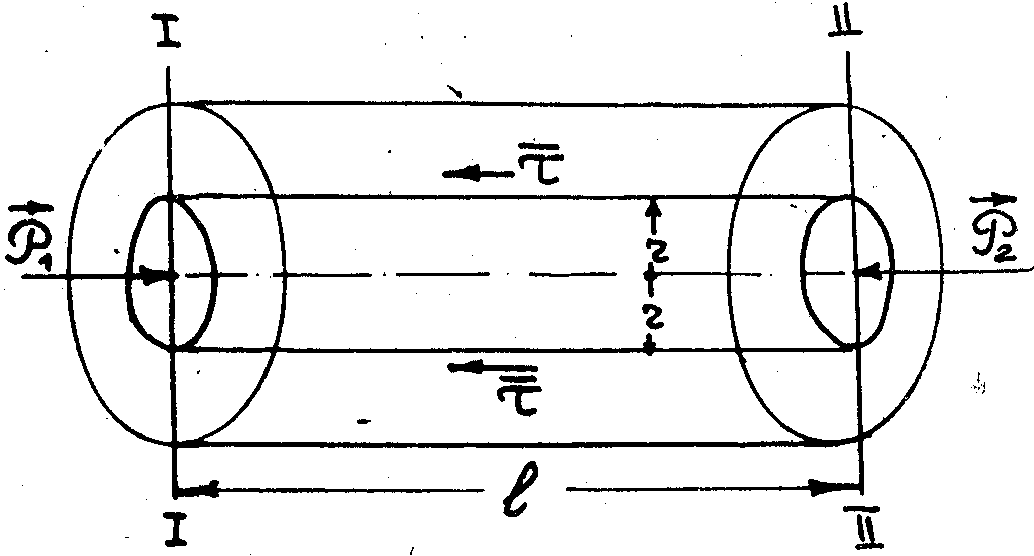
Рис. 3.1.
Рассмотрим силы, действующие на выделенный цилиндр. В сечении (1 – 1) действует сила давления P1 = p1πr2, в сечении (2 – 2) – сила Р2 = p2πr2; p1 и p2 давления в сечениях (1 – 1) и (2 – 2). На боковую поверхность цилиндра действует сила трения Т = 2πrlτ, где τ – среднее по периметру касательное напряжение. Кроме того, на выделенный объем жидкости действует сила инерции, равная массе жидкости выделенного объема М, умноженной на ускорение движения его центра тяжести ас со знаком "минус".
Уравнение равновесия всех сил в проекции на ось трубы имеет вид:
(p1 –p2) πr2 - 2πrlτ + (-M ас) = 0. (3.2)
Так как движение
установившееся, то
,
а из уравнения неразрывности следует,
что
.
Следовательно,
Из (3.2) получим, что
(Δp
= p1
- p2) (3.3)
Обозначим через
среднее
по периметру трубы напряжение трения.
Тогда
(3.4)
где а — радиус трубы. Из (3.3) и (3.4) следует
(3.5)
Соотношение (3.5) показывает линейность связи между касательным напряжением и радиусом сечения трубы.
Распределение скорости в сечении трубы.
Запишем реологическое уравнение (3.1) в виде:
(3.6)
Проинтегрируем (3.6) по r от а до r. При r = а, скорость считаем равной нулю (условие прилипания):
(3.7)
Имеем
(3.8)
при r = а, τ = τа; при r = r; τ = τ. Тогда из (3.7) получим
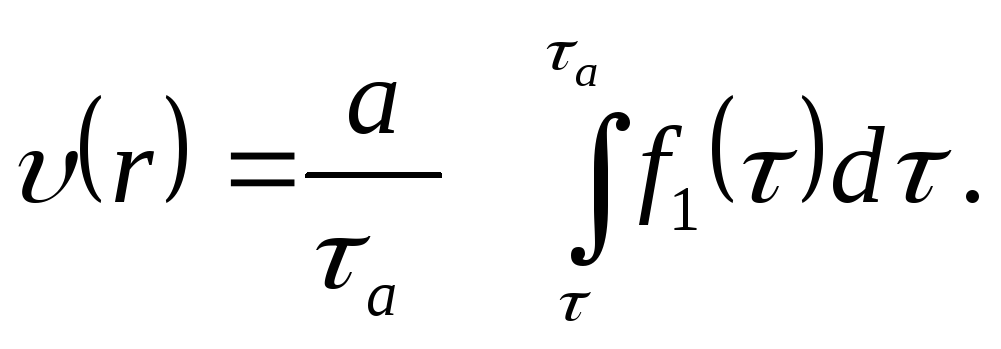(3.9)
Таким образом, мы получили формулу, дающую закон распределения скорости жидкости по радиусу при любом виде функции f1(τ).
Определение расхода жидкости.
Для определения расхода жидкости найдем элементарный объемный расход через сечение, заключенное между концентрическими окружностями с радиусами r и r+dr.
Чтобы определить полный расход, проинтегрируем полученное соотношение
(3.10)
Интегрируем (3.10) по частям:
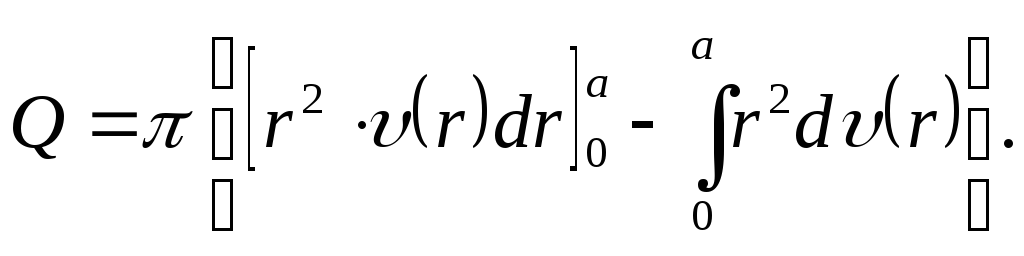
Учитывая, что
(a)
= 0 и dυ
= -f1(τ)dr
и пользуясь формулами (3.8), получим
Или окончательно
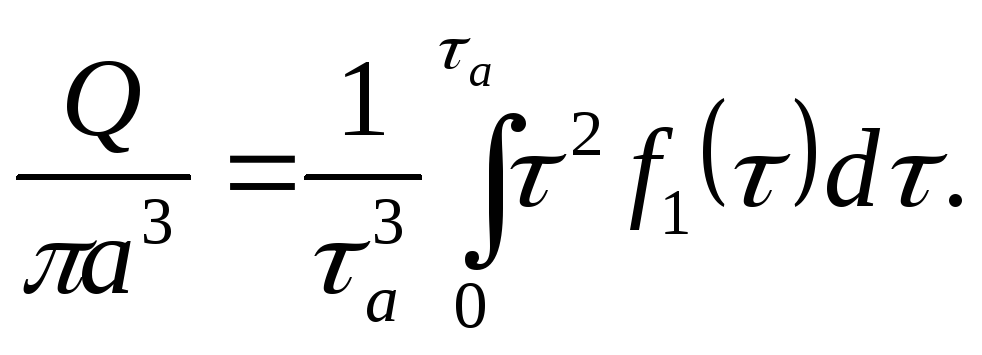(3.11)
Итак, определен расход жидкости в трубе при любом виде функции f1(τ). Рассмотрим несколько примеров.
Движение вязкой ньютоновской жидкости
При ламинарном течении вязкой ньютоновской жидкости в трубе
Следовательно,
Распределение скорости по сечению трубы.
По формуле (3.9) вычислим скорость
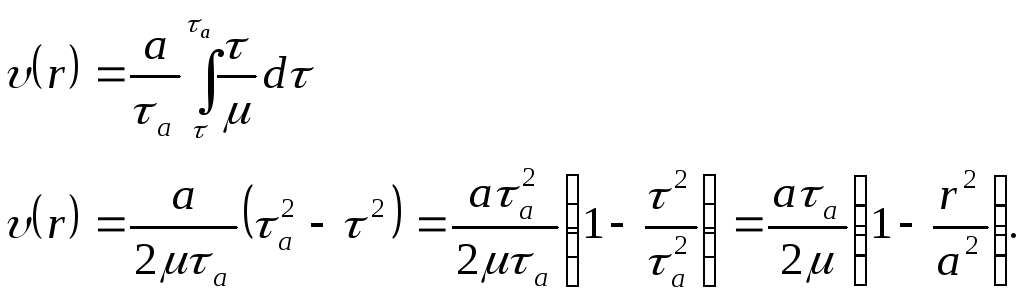
Используя (3.4), получим
(3.12)
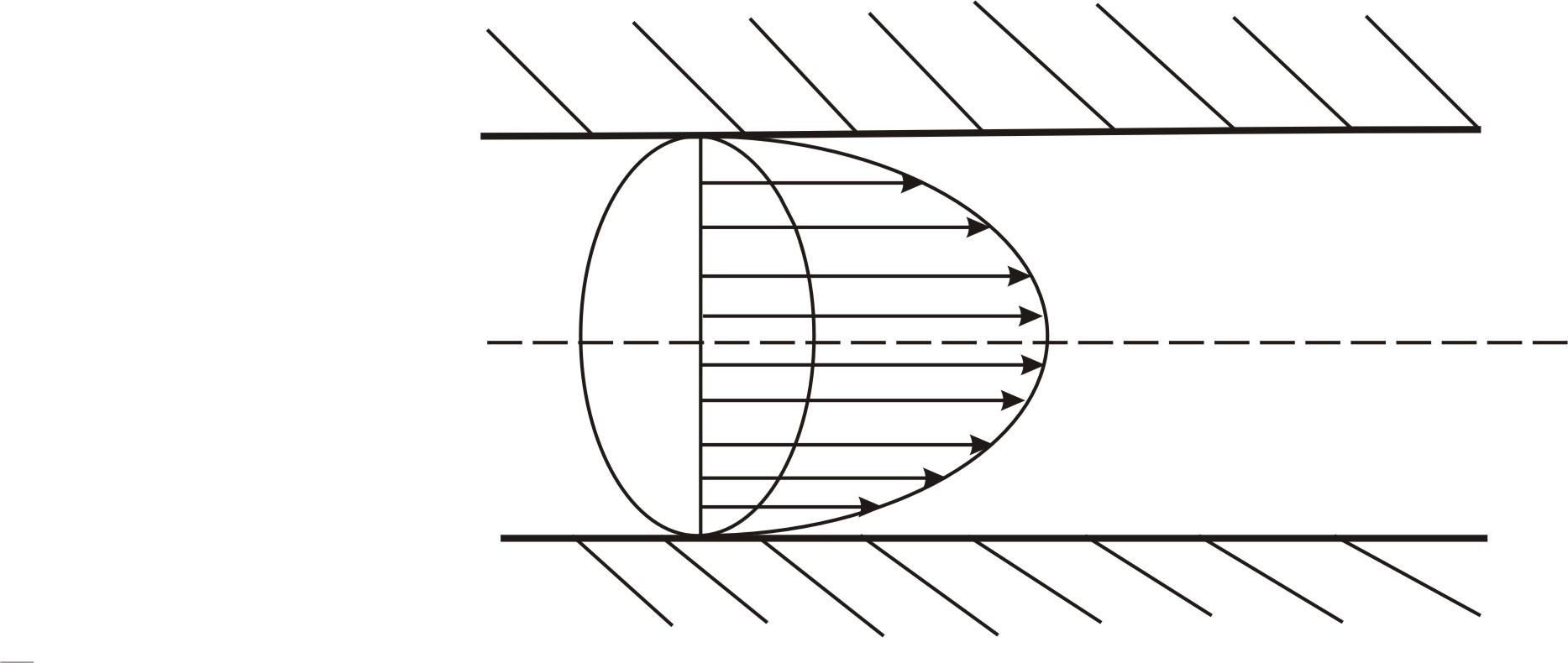
Рис. 3.2.
Следовательно, эпюрой скорости является параболоид вращения с меридиональным сечением, представляющим собой параболу (рис. 3.2).
Максимальная скорость υo достигается на оси трубы (при r=0) и равна:
(3.13)
Поэтому распределение скоростей можно записать в виде
(3.14)
Определение расхода.
Расход вязкой ньютоновской жидкости определим по формуле (3.11), считая, что f1=τ/μ
Используя соотношение (3.4), получим:
(3.15)
Соотношение (3.15) называется формулой Пуазейля по имени французского врача и физиолога, исследовавшего законы движения крови по капиллярным сосудам и получившего это соотношение.
Закон Пуазейля (3.15) показывает, что при установившемся ламинарном движении вязкой ньютоновской жидкости в круглой трубе объемный расход пропорционален перепаду давления на единицу длины трубы и четвертой степени ее радиуса.
Расход можно записать через осевую скорость υo, используя соотношение (3.13). Получим
.
(3.16)
Выражая расход Q через среднюю скорость w
(3.17)
и сравнивая (3.16) и (3.17) получим, что
то есть средняя скорость движения равна половине осевой скорости.
Движение вязкопластичной жидкости в круглой трубе
Реологическое уравнение вязкопластичной жидкости имеет вид
(3.18)
При этом
при
при
Напомним, что здесь τo — предельное касательное напряжение, после достижения которого начинается течение жидкости. При течении в трубе напряжение трения τ меняется по радиусу от максимального значения на стенке, уменьшаясь к оси трубы. Но при τ < τ0 вязкопластичная жидкость ведет себя как твердое тело, то есть течение отсутствует. Следовательно, в центре трубы вязкопластичная жидкость будет двигаться как твердый стержень.
Распределение скорости по сечению трубы.
Распределение скорости получим, воспользовавшись формулой (3.9) и учитывая, что ƒ1(τ) определяется по (3.18):
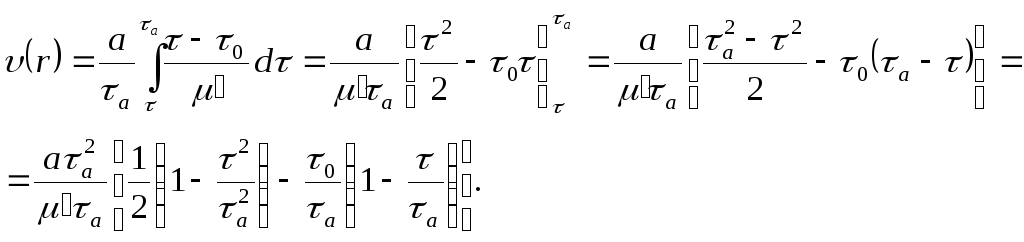
Учитывая, что
(формулы (3.4) и (3.5)) после несложных преобразований получим:
Обозначим радиус сечения, на котором касательное напряжение становится равным τo, через ro
Эпюра скоростей будет иметь вид
(3.19)
при ro<r<а и
(3.20)
при 0 < r ro.
Следовательно, эпюра скоростей состоит частью из поверхности параболоида вращения (от стенки трубы до цилиндрической поверхности радиуса ro), а частью из плоской площадки, перпендикулярной к оси трубы (в центральной части трубы) (рис. 3.3). В центральной части трубы вязкопластичная жидкость движется как твердый стержень.
Если в равенствах (3.19) и (3.20) положить τo = 0, т. е. перейти к ньютоновской вязкой жидкости, то получим известный параболоид вращения, а плоская площадка исчезнет.
Рис. 3.3.
Расход вязкопластичной жидкости.
Для определения расхода подставим ƒ1(τ) (формула (3.18)) в соотношение (3.11)
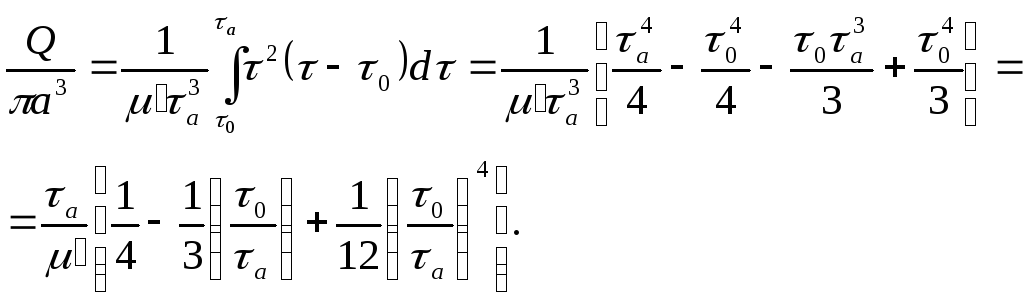
Заменяя здесь τа его выражением через Δр по (3.4), получим формулу Букингема.
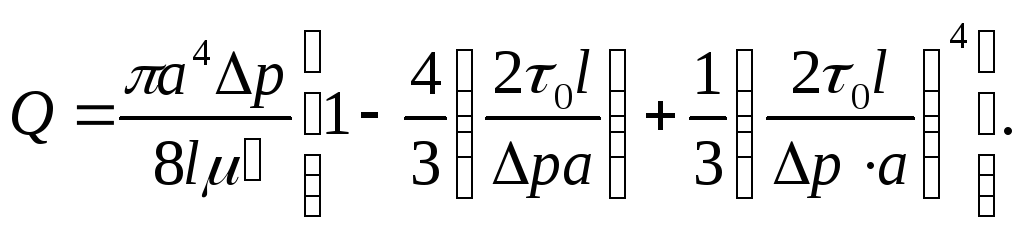(3.21)
При τo=0 получим уже известную формулу Пуазейля (3.15).
Движение жидкости, подчиняющейся степенному реологическому закону
Псевдопластичные и дилатантные жидкости описываются степенным реологическим уравнением:
(3.22)
Из (3.22) находим, что
(3.23)
Распределение скорости в сечении.
Подставляя (3.23) в (3.9) получим,
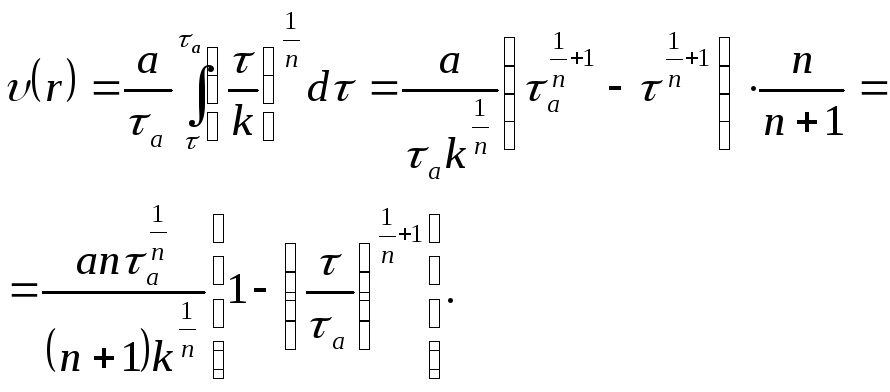
Используя формулы (3.4) и (3.5), определим
. (3.24)
Определение расхода.
Расход определим по формуле (3.11), учитывая (3.23). Получим
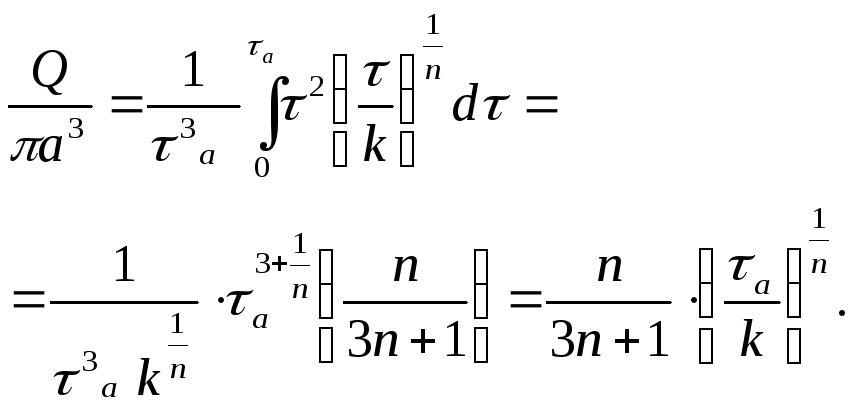(3.25)
Подставляя (3.4) в (3.25), получим
. (3.26)
Для вязкой ньютоновской жидкости (n=1), уравнение (3.26) превращается в формулу Пуазейля (3.15).