Вдовин Валерий, 3 курс
РГР: Устойчивость НУШ-солитона вторым методом Ляпунова с явной оценкой через норму возмущения
1. Доказательство устойчивости
Постановка задачи
Для нестационарного уравнения Шредингера
(1)
Известны точные решения – солитоны. Нужно доказать их устойчивость.
Некоторые сведения о солитонах
Солитоны – точные решения уравнения (1).
Неподвижный солитон:
(2)
где
.
Подвижный солитон:
(3)
где
.
При этом неподвижный солитон находится из уравнения
, (4)
а подвижный – из уравнения
. (5)
Поскольку функция
чисто действительна, то мы сразу получаем
условие
,
а уравнение принимает вид
, (6)
где
.
Следует заметить, что по построению имеем:
(7)
(8)
Интегралы движения.
Нестационарному уравнению Шредингера соответствует действие
, (9)
где лагранжиан L равен
. (10)
Тогда тензор энергии-импульса имеет вид («Теория поля» Ландау и Лифшица, с. 109-113)
, (11)
где индексы k,
j обозначают одну из
двух переменных t, x.
Тогда выполняется условие
(11а)
Действительно,
,
подставим сюда уравнения
движения
,
тогда
,
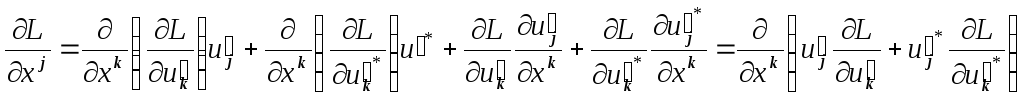заменим в левой части
,
подставим обозначение (11) и как раз
получим (11а).
Тогда в нашем случает тензор примет вид:
(12)
Из условия (11а) следует, что
сохраняются величины
(энергия) и
(импульс). Поэтому:
– интеграл энергии, (13)
– интеграл импульса. (14)
Интеграл «массы» (он же интеграл числа квантов) имеет вид
(15)
Его сохранение следует из
того, что лагранжиан L
не зависит явно от фазы функции u. Интеграл
(15) легко получить явно, помножив уравнение
на
и проинтегрировав по x.
Построение функционала Ляпунова.
Логично пытаться строить функционал Ляпунова на основе функционала энергии. Однако он не ограничен сверху из-за функций вида
, (16)
поскольку при росте
при постоянных A
и D
функционал энергии
неограниченно растет. Он также неограничен
снизу из-за функции
, (17)
при росте A
при постоянной D
функционал энергии
неограниченно убывает.
Если же рассмотреть функционал
энергии при условии сохранения числа
квантов («массы»)
,
то он будет по-прежнему неограничен
сверху (поскольку при больших
интеграл
слабо зависит от
,
это легко компенсировать подбором
параметра A).
При этом функционал окажется ограниченным
снизу (пример вида
теперь не подходит, поскольку
и мы не можем стремить амплитуду функции
к бесконечности оставляя ширину ее
постоянной).
Оценка с помощью неравенства Соболева.
Введем обозначение
. (18)
По неравенству Соболева:
. (19)
Тогда
– квадратный трехчлен от
.
Минимум выражения в правой части
достигается при
,
что дает оценку:
. (20)
Ясно, что оценка неточна, поскольку неравенство Соболева обращается в равенство на функциях вида
, (21)
с учетом
получаем
, (22)
однако для такой (как и почти
любой) функции
(равенство достигается для функций вида
прямоугольника).
В результате значение
функционала
существенно больше, а именно:
. (23)
Точная оценка.
Для получения точной оценки
нужно решить вариационную задачу на
условный экстремум. Варьируя
получаем систему:
, (24)
где P – заданная константа.
Отсюда сразу следует быстрое
спадание функции u
на
.
Если искать решение в классе действительных
функций, то сразу ясно что это сепаратрисное
решение, задачу легко решить. Можно
заметить, что это уравнение для солитона
(4), тогда можно сразу написать простейшее
решение (для
)
вида
.
Из условия
получаем
,
тогда
. (25)
Подставив найденное решение
в функционал
,
найдем его точную оценку
. (26)
Как и следовало ожидать,
.
Для получения точной оценки
функционала достаточно было найти хотя
бы одно решение системы (24). Однако для
дальнейшего важно, что системе
удовлетворяют неподвижный солитон (2)
при условии
.
Это означает, что на этих функциях
функционал энергии принимает минимальное
значение (при условии сохранения числа
квантов
).
Явный вид функционала Ляпунова.
Теперь можно ввести функционал
Ляпунова:
(27)
При сохранении
минимум функционала Ляпунова достигается
именно на солитонах по построению, тогда
именно в окрестности солитона при
сохранении
выполняются условия
,
,
. (28)
Поскольку функционал Ляпунова сконструирован из интегралов движения, то он неизменен во времени:
, (29)
что доказывает устойчивость
солитонов. Вообще, если функционал
(при условии
)
принимает свое минимальное значение
на каком-то семействе функций, то мы
получаем доказательство устойчивости
тех функций этого семейства, которые
удовлетворяют уравнению НУШ.
Мы уже доказали устойчивость солитонов, но желательна еще оценка второй вариации через норму возмущения. Эта оценка позволит установить количественную связь между значением функционала Ляпунова на возмущенной траектории и нормой возмущения, чтобы можно было описать устойчивость солитона в терминах неувеличения нормы возмузщения…