4.5.1. Ковариация и коэффициент корреляции.

Между случайными величинами может существовать функциональная или стохастическая (вероятностная) зависимость. Стохастическая зависимость проявляется в том, что условный закон распределения одной случайной величины изменяется в зависимости от значений, принимаемых другой случайной величиной. Одной из характеристик стохастической зависимости двух случайных величин является ковариация случайных величин.

Ковариацией случайных величин (X,Y) называется число равное математическому ожиданию произведения отклонений случайных величин X и Y от своих математических ожиданий:

.

Иногда ковариацию называют корреляционным моментом или вторым смешанным центральным моментом случайных величин (X,Y).

Используя определение математического ожидания, получим:

для дискретного распределения

,

для непрерывного распределения

.

При Y = X ковариация совпадает с дисперсией Х.

Величина корреляционного момента зависит от единиц измерения случайных величин. Это затрудняет сравнение корреляционных моментов различных систем случайных величин. Для устранения этого недостатка вводится новая числовая характеристика – коэффициент корреляции , который является

безразмерной величиной.

Для его вычисления заменим отклонения случайных величин от математических ожиданий их нормированными отклонениями, т.е.

.

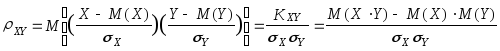Свойства коэффициента корреляции:

1. 

Пусть t – переменная величина в смысле математического анализа. Рассмотрим дисперсию случайной величины D(Y – tX) как функцию переменной t .

По свойству дисперсии . Дискриминант в этом случае должен быть меньше либо равен нулю, т.е.

, откуда получим

2. Модуль коэффициента корреляции не меняется при линейных преобразованиях случайных переменных: 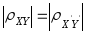, где 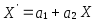, , 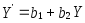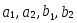– произвольные числа.

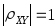3. , тогда и только тогда, когда случайные величины X и Y связаны линейно, т.е. существуют такие числа a, b, что .

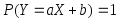Если , то рассматриваемый в п.1 дискриминант равен нулю, а поэтому при некотором значение . Следовательно, величина и для некоторого С справедливо равенство , что требовалось доказать.

4. Если X и Y статистически независимы, то .

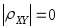Свойства 2,4 проверяются непосредственно.

2. Коррелированность и зависимость системы случайных величин.

Необходимым условием независимости случайных величин X и Y является равенство нулю их корреляционного момента (или коэффициента корреляции). Однако равенство (или ) есть только необходимое, но недостаточное условие независимости.

Пример 1.

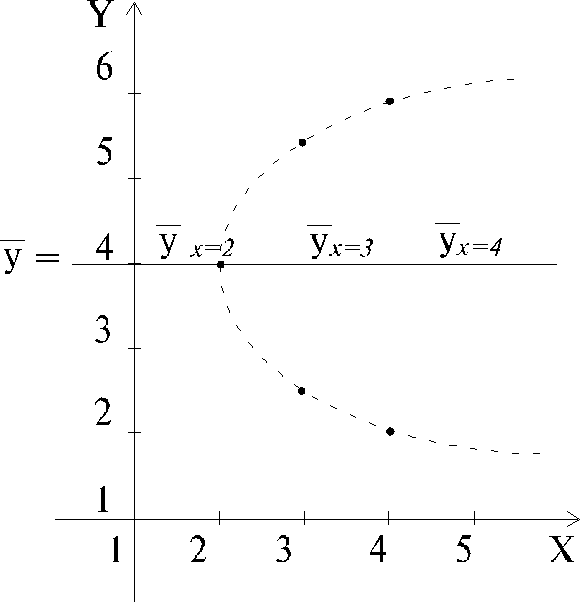
На рисунке изображены точки, лежащие на параболе , а.

В связи с этим вводится более узкое понятие некоррелированности (если) или коррелированности (если ) случайных величин. Поэтому независимость случайных величин означает и некоррелированность () и, наоборот, коррелированность () – зависимость.

В общем случае, когда , точки (X,Y) будут разбросаны вокруг прямой тем более тесно, чем больше величина . Таким образом, коэффициент корреляции характеризует не любую зависимость между X и Y, а степень тесноты линейной зависимости между ними.

Так, в частности, даже при , т.е. при полном отсутствии линейной зависимости, между X и Y может существовать сколь угодно сильная статистическая и даже нелинейная функциональная зависимость (см. пример1).

При значениях говорят о положительной корреляции между X и Y, означающей, что обе переменные имеют одинаковую тенденцию к возрастанию или убыванию. При говорят об отрицательной корреляции, означающей противоположную тенденцию в изменении случайных величин X и Y, т.е. одна возрастает, а другая убывает или наоборот.

Если случайные величины X и Y распределены нормально, то из их некоррелированности следует и их независимость, так как

.

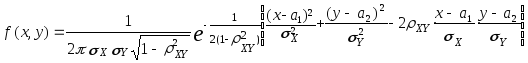Если, то .

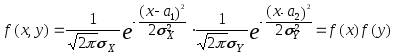Для вычисления коэффициента корреляции продолжим пример 2 из §4.1. Воспользуемся формулой

.

M(XY)=(-200)(-100)0,2 + (-200)00,1 + (-200)(100)0,05 + 0(-100)0,05 + 000,25 + 01000,02 + 200(-100)0,01 + 20000,02 + 2001000,3 = 8800$;

;

;

; ;

.

Пример 2. Закон распределения системы двух случайных величин задан таблицей распределения

X Y	0	1	2	3
-1	0,01	0,06	0,05	0,04
0	0,04	0,24	0,15	0,07
1	0,05	0,01	0,01	0,09

Найти одномерные (маргинальные) законы распределения X и Y, их математические ожидания, дисперсии и коэффициент корреляции между X и Y.

Решение. Вероятности возможных значений дискретной случайной величины Х, входящей в систему, определяются формулой

, к=1, 2, 3, 4.

Поэтому одномерное распределение величины Х имеет следующий вид

X	0	1	2	3
	0,1	0,4	0,3	0,2	1,0

Аналогично, пользуясь формулой

, i=1, 2, 3 ,

получим одномерное распределение величины Y

Y	-1	0	1
	0,16	0,50	0,34	1,0

Математические ожидания случайных величин X и Y:

M(X)=1,6; M(Y)=0,18.

Дисперсии случайных величин X и Y:

D(X)=0,84; D(Y)=0,47.

Коэффициент корреляции между X и Y вычисляется по формуле

; ;

; ;