
- •Задачи для самостоятельного решения
- •9. Определенный интеграл
- •10. Применение определенных интегралов. Несобственные интегралы
- •Объем тела вращения
- •Длина дуги плоской кривой
- •Несобственные интегралы с бесконечными пределами интегрирования
- •Несобственные интегралы от неограниченных функций
- •Задачи для самостоятельного решения
- •10. Применение определенных интегралов. Несобственные интегралы
- •11. Дифференциальные уравнения
- •Дифференциальные уравнения первого порядка. Задача Коши
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •Линейные дифференциальные уравнения
- •Метод подстановки (метод Бернулли)
- •Задачи для самостоятельного решения
- •11. Дифференциальные уравнения
- •12. Числовые ряды
- •Ряды с положительными членами. Признаки сходимости
- •Знакочередующиеся ряды. Признак сходимости Лейбница
- •Знакопеременные ряды
- •Задачи для самостоятельного решения
- •12. Числовые ряды
- •13. Степенные ряды
- •Содержание
- •Минченков Юрий Владимирович высшая математика Сборник задач по математическому анализу
- •220086, Минск, ул. Славинского, 1, корп. 3.
Знакочередующиеся ряды. Признак сходимости Лейбница
Определение 4. Знакочередующимся рядом называется ряд, у которого любые рядом стоящие члены имеют противоположные знаки.
Такие ряды удобнее записывать в виде
![]() (6)
(6)
или в виде
![]() ,
(7)
,
(7)
где
![]()
Для определения сходимости знакочередующихся рядов существует достаточный признак.
Теорема 6. (Достаточный признак сходимости Лейбница). Для того чтобы знакочередующийся ряд (6)((7)) сходился, достаточно, чтобы абсолютные значения его членов убывали и стремились к нулю при возрастании n.
Таким образом,
если
![]() и
и
![]() то знакочередующийся ряд (6)((7)) сходится.
то знакочередующийся ряд (6)((7)) сходится.
Пример 8. Ряд
![]()
сходится, так как для него выполняются все условия признака сходимости Лейбница.
Знакопеременные ряды
Рассмотрим числовые ряды
![]() (8)
(8)
с произвольными членами, т. е. члены ряда могут быть как положительными, так и отрицательными. Такие ряды называются знакопеременными.
Определение 5. Ряд (8) называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов.
Определение 6. Ряд (8) называется условно сходящимся, если ряд (8) сходится, а ряд, составленный из его абсолютных величин, расходится.
Задачи для самостоятельного решения
12. Числовые ряды
1. Найти сумму ряда:
а)
![]() ;
б)
;
б)
![]() в)
в)
![]()
2. Исследовать сходимость ряда, пользуясь необходимым признаком и признаком сравнения:
а)
![]() б)
б)
![]()
![]() в)
в)
![]() ;
г)
;
г)![]()
3. Исследовать сходимость ряда по признаку Даламбера:
а)
![]() б)
б)
![]() в)
в)
![]() ;
г)
;
г)
![]() .
.
4. Исследовать сходимость ряда по признаку Коши:
а)
![]() б)
б)
![]() ;
в)
;
в)
![]() г)
г)
![]() .
.
5. Исследовать, сходятся абсолютно или условно или расходятся знакопеременные ряды:
а)
![]() б)
б)
![]() в)
в)
![]() .
.
13. Степенные ряды
Определение 1. Степенным рядом называется функциональный ряд вида
![]() . (1)
. (1)
Здесь
![]() – постоянные действительные числа,
называемые
коэффициентами
степенного ряда; а
– некоторое постоянное число,
х
– переменная, принимающая значения из
множества действительных чисел.
– постоянные действительные числа,
называемые
коэффициентами
степенного ряда; а
– некоторое постоянное число,
х
– переменная, принимающая значения из
множества действительных чисел.
При
![]() степенной ряд (1) принимает вид
степенной ряд (1) принимает вид
![]() .
(2)
.
(2)
Степенной ряд (1)
называют рядом
по степеням разности
![]() ,
ряд (2) – рядом
по степеням
х.
,
ряд (2) – рядом
по степеням
х.
Если переменной х придать какое-либо значение, то степенной ряд (1) (или (2)) превращается в числовой ряд, который может сходиться или расходиться.
Определение 2. Областью сходимости степенного ряда называется множество значений х, при которых степенной ряд сходится.
Теорема
1.
(Теорема Абеля).
Если степенной
ряд (2) сходится при
![]() ,
то
он абсолютно сходится при всех значениях
х, удовлетворяющих неравенству
,
то
он абсолютно сходится при всех значениях
х, удовлетворяющих неравенству
![]() ;
если же ряд (2) расходится при
;
если же ряд (2) расходится при
![]() ,
то он расходится при всех значениях х,
удовлетворяющих неравенству
,
то он расходится при всех значениях х,
удовлетворяющих неравенству
![]() .
.
Теорема Абеля дает ясное представление о структуре области сходимости степенного ряда.
Теорема 2. Область сходимости степенного ряда (2) совпадает с одним из следующих интервалов:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ,
,
где R
– некоторое неотрицательное действительное
число или
![]() .
.
Число
R
называется радиусом
сходимости,
интервал
![]() – интервалом
сходимости
степенного ряда (2).
– интервалом
сходимости
степенного ряда (2).
Если
![]() ,
то интервал сходимости представляет
собой всю числовую ось
,
то интервал сходимости представляет
собой всю числовую ось
![]() .
.
Если
![]() ,
то интервал сходимости вырождается в
точку
,
то интервал сходимости вырождается в
точку
![]() .
.
Замечание:
если
![]() – интервал сходимости для степенного
ряда (2), то
– интервал сходимости для степенного
ряда (2), то
![]() – интервал сходимости для степенного
ряда (1).
– интервал сходимости для степенного
ряда (1).
Радиус сходимости R степенного ряда можно найти по одной из следующих формул:
формула Даламбера:
![]() ; (3)
; (3)
формула Коши:
 . (4)
. (4)
Если в формуле
Коши
![]() ,
то полагают
,
то полагают
![]() ,
если
,
если
![]() ,
то полагают
,
то полагают
![]() .
.
Пример 1. Найти
радиус сходимости, интервал сходимости
и область сходимости степенного ряда
![]() .
.
Решение
Найдем радиус
сходимости данного ряда по формуле
![]() .
В нашем случае
.
В нашем случае
![]() ,
,
![]() .
.
Тогда
![]() .
.
Следовательно,
интервал сходимости данного ряда имеет
вид
![]() .
.
Исследуем сходимость ряда на концах интервала сходимости.
При
![]() степенной ряд превращается в числовой
ряд
степенной ряд превращается в числовой
ряд
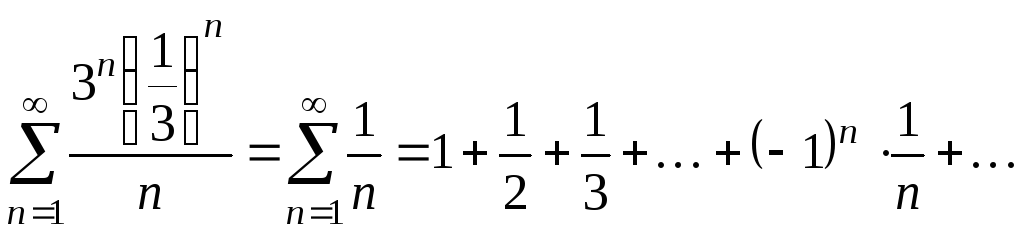 .
.
который расходится как гармонический ряд.
При
![]() степенной ряд превращается в числовой
ряд
степенной ряд превращается в числовой
ряд
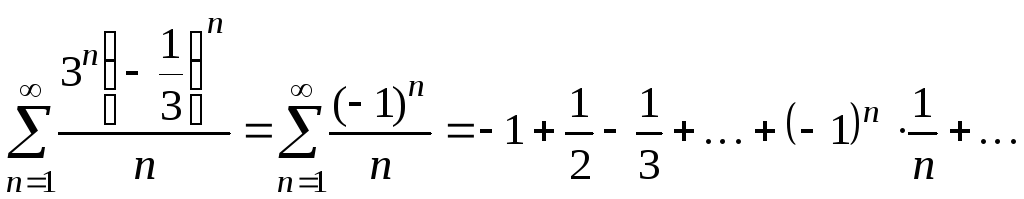 .
.
Это – знакочередующийся
ряд, члены которого убывают по абсолютной
величине и
![]() .
Следовательно, по признаку Лейбница
этот числовой ряд сходится.
.
Следовательно, по признаку Лейбница
этот числовой ряд сходится.
Таким образом,
промежуток
![]() – область сходимости данного степенного
ряда.
– область сходимости данного степенного
ряда.
Ряды Тейлора и Маклорена
Пусть
![]() – дифференцируемая бесконечное число
раз функция
в окрестности точки
– дифференцируемая бесконечное число
раз функция
в окрестности точки
![]() ,
т. е. имеет производные любых порядков.
,
т. е. имеет производные любых порядков.
Определение 3.
Рядом
Тейлора
функции
![]() в точке
в точке
![]() называется степенной ряд
называется степенной ряд
![]()
![]() .
(5)
.
(5)
В частном случае
при
![]() ряд (5) называется рядом
Маклорена:
ряд (5) называется рядом
Маклорена:
![]() .
.
Разложение некоторых элементарных
функций в ряд Маклорена
1.
![]() .
.
2.
![]() .
.
3.
![]()
4.
![]() – логарифмический
ряд.
– логарифмический
ряд.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
13. Степенные ряды
1. Найти радиус сходимости, интервал сходимости, область сходимости степенного ряда:
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
2. Разложить в ряд Маклорена следующие функции:
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]()
![]() ;
;
г)
![]()
![]() ; д)
; д)
![]() ; е)
; е)
![]() .
.
ОТВЕТЫ К ЗАДАЧАМ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Предел последовательности
1. а) 6997, б) 98, в) 199, г) 5498, д) 348.
2.
а)
![]() ,
б) 0, в) 2, г) 0, д) 0, е)
,
б) 0, в) 2, г) 0, д) 0, е)
![]() ,
ж)
,
ж)
![]() ,
з) 1, и) 2, к)
,
з) 1, и) 2, к)
![]() ,
л)
,
л)
![]() ,
м) 2.
,
м) 2.
3.
а) 4, б) 1, в)
![]() ,
г) 0, д)
,
г) 0, д)
![]() ,
е)
,
е)
![]() ,
ж)
,
ж)
![]() ,
з) 0.
,
з) 0.
4.
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() ,
д)
,
д)
![]() ,
е)
,
е)
![]() ,
ж)
,
ж)
![]() ,
з)
,
з)
![]() ,
)
,
)
![]() ,
к)
,
к)
![]() .
.
2. Предел функции
1.
а) 1, б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() ,
д)
,
д)
![]() ,
е)
,
е)
![]() ,
ж)
,
ж)
![]() ,
з)
,
з)
![]() ,
и)
,
и)
![]() .
.
2.
а)
![]() ,
б)
,
б)
![]() ,
в) 2, г)
,
в) 2, г)
![]() ,
д)
,
д)
![]() ,
е)
,
е)
![]() ,
ж)
,
ж)
![]() ,
з)
,
з)
![]() ,
и)
,
и)
![]() ,
к) 5.
,
к) 5.
3.
а) 1, б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() ,
д)
,
д)
![]() ,
е)
,
е)
![]() .
.
3. Непрерывность функции в точке
1.
а)
![]() – точка разрыва второго рода;
– точка разрыва второго рода;
![]() – точка непрерывности функции; б)
– точка непрерывности функции; б)
![]() – точка непрерывности функции;
– точка непрерывности функции;
![]() – точка разрыва второго рода.
– точка разрыва второго рода.
3. а)
![]() – точка устранимого разрыва; б)
– точка устранимого разрыва; б)
![]() – точка разрыва первого рода.
– точка разрыва первого рода.
4. а)
![]() – точка разрыва второго рода; б)
– точка разрыва второго рода; б)
![]() – точка разрыва второго рода.
– точка разрыва второго рода.
4. Производная функции
1.
![]() 2.
2.
![]() 3.
3.
![]() 4.
4.
![]() 5.
5.
![]()
![]()
![]() 6.
10 cos
10x.
7.
6.
10 cos
10x.
7.
![]() .
8.
.
8.
![]() 9.
9.
![]() 10.
10.
![]() 11.
11.
![]() 12.
12.
![]() 13.
13.
![]() 14.
14.
![]() 15.
15.
![]() 16.
16.
![]() 17.
17.
![]() 18.
18.
![]() 19.
19.
![]() 20.
0. 21.
20.
0. 21.
![]() 22.
22.
![]()
5. Правило Лопиталя. Дифференциал функции
1.
0. 2.
0. 3.
![]() 4.
–3. 5.
1. 6.
1. 7.
4.
–3. 5.
1. 6.
1. 7.
![]() 8. 1. 9.
8. 1. 9.
![]() 10.
0,515. 11.
1,3. 12.
1,067. 13. 2,0125.
10.
0,515. 11.
1,3. 12.
1,067. 13. 2,0125.
6. Исследование функции
1.
![]()
2.
![]() .
.
3.
![]()
4.
![]() – точки перегиба.
– точки перегиба.
5.
![]() – точки перегиба.
– точки перегиба.
6.
![]() – точки перегиба.
– точки перегиба.
7. х = 0, у = х.
8. х = –1, у = х – 1.
9. у = 1.
7. Функции нескольких переменных
1. а)
![]() ;
;
![]() ;
;
б)
![]() ;
;
![]() ;
;
в)
![]() ;
;
![]() ;
;
г)
![]() ;
;
![]() ;
;
д)
![]() ;
;
![]() ;
;
е)
![]() ;
;
![]() ;
;
ж)
![]() ;
;
![]() ;
;
з)
![]() ;
;
![]() ;
;
и)
![]() ;
;
![]() .
.
2. а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ;
е)
;
е)
![]() .
.
4. а)
![]() ;
;
![]() ;
;
![]() ;
;
б)
![]() ;
;
![]() ;
;
![]() ;
;
в)
![]() ;
;
![]() ;
;
![]() ;
;
г)
![]() ;
;
![]() ;
;
![]() .
.
5. а)
![]() ;
б)
;
б)
![]() ;
в) экстремумов
нет;
г)
;
в) экстремумов
нет;
г)
![]() ;
д)
;
д)
![]() ;
в точке
;
в точке
![]() функция экстремума не имеет.
функция экстремума не имеет.
8. Неопределенный интеграл
1. а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
2. а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ;
е)
;
е)
![]() .
.
3. a)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ;
е)
;
е)
![]() .
.
4. а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ;
е)
;
е)
![]() .
.
5. а)
![]() ;
б)
;
б)
![]() ;
;
в)
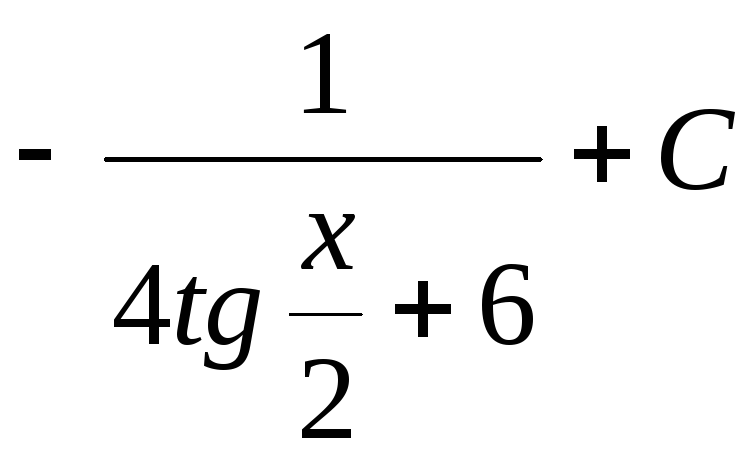 ;
г)
;
г)
![]() ;
;
д)
![]() ;
е)
;
е)
![]() .
.
9. Определенный интеграл
1. а)
![]() ;
б)
1; в)
6; г)
1; д)
;
б)
1; в)
6; г)
1; д)
![]() ;
е)
;
е)
![]() ;
ж)
;
ж)
![]() ;
з)
40 .
;
з)
40 .
2. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
3. a)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() .
.
10. Применение определенных интегралов. Несобственные интегралы
1. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() .
.
2. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
3. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
4. а)
![]() ;
б)
;
б)
![]() .
.
5. а) 1;
б)
расходится; в)
![]() ;
г)
расходится; д)
;
г)
расходится; д)
![]() ;
е)
0,5; ж)
2; з)
;
е)
0,5; ж)
2; з)
![]() ;
и) расходится;
к)
расходится; л)
–1; м)
расходится.
;
и) расходится;
к)
расходится; л)
–1; м)
расходится.
11. Дифференциальные уравнения
1.
![]() .
2.
.
2.
![]() .
3.
.
3.
![]() .
4.
.
4.
![]() .
5.
.
5.
![]() .
6.
.
6.
![]() .
7.
.
7.
![]() .
8.
.
8.
![]() .
9.
.
9.
![]() .
10.
.
10.
![]() .
11.
.
11.
![]() .
12.
.
12.
![]() .
13.
.
13.
![]() .
14.
.
14.
![]() .
15.
.
15.
![]() .
16.
.
16.
![]() .
17.
.
17.
![]() .
18.
.
18.
![]() .
19.
.
19.
![]() .
20.
.
20.
![]() .
21.
.
21.
![]() .
22.
.
22.
![]() .
23.
.
23.
![]() .
24.
.
24.
![]() .
.
12. Числовые ряды
1. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
2. а) расходится; б) расходится; в) сходится; г) расходится.
3. а) расходится; б) сходится; в) сходится; г) сходится.
4. а) сходится; б) сходится; в) расходится; г) сходится.
5. а) сходится условно; б) расходится; в) расходится.
13. Степенные ряды
1. a) R = 1, (–1; 1) – интервал и область сходимости;
б) R = , ряд абсолютно сходится на всей числовой оси;
в) R = 1, (–1; 1) – интервал сходимости, [–1; 1] – область сходимости;
г) R = 0, ряд сходится только в точке х = 0.
Литература
-
Гусак А. А. Справочное пособие к решению задач. Математический анализ и дифференциальные уравнения. – Мн.: ТетраСистемс, 1998.
-
Минченков Ю. В. Высшая математика. Теория пределов: Учебно-методическое пособие. – Мн.: Частн. ин-т упр. и предпр., 2005. – 20 с.
-
Минченков Ю. В. Высшая математика. Производная функции. Дифференциал функции: Учебно-методическое пособие. – Мн.: Частн. ин-т упр. и предпр., 2007. – 20 с.
-
Минченков Ю. В. Высшая математика. Исследование функций: Учебно-методическое пособие. – Мн.: Частн. ин-т упр. и предпр., 2007. – 23 с.
-
Метельский В. М. Высшая математика. Непрерывность функции. Функции нескольких переменных: Учебно-методическое пособие. – Мн.: Частн. ин-т упр. и предпр., 2005. – 24 с.
-
Метельский В. М. Высшая математика. Неопределенный интеграл: Учебно-методическое пособие. – Мн.: Частн. ин-т упр. и предпр., 2007. – 28 с.
-
Метельский В. М. Высшая математика. Определенный интеграл: Учебно-методическое пособие. – Мн.: Частн. ин-т упр. и предпр., 2007. – 28 с.
-
Минченков Ю. В. Высшая математика. Дифференциальные уравнения: Учебно-методическое пособие. – Мн.: Частн. ин-т упр. и предпр., 2007. – 27 с.
-
Овсеец М. И., Светлая Е. М. Высшая математика. Числовые ряды: Учебно-методическое пособие. – Мн.: Частн. ин-т упр. и предпр., 2005. – 20 с.
-
Овсеец М. И., Светлая Е. М. Высшая математика. Степенные ряды: Учебно-методическое пособие. – Мн.: Частн. ин-т упр. и предпр., 2006. – 13 с.
