
- •1. Предел последовательности
- •Основные способы вычисления пределов
- •Задачи для самостоятельного решения
- •1. Предел последовательности
- •2. Предел функции Определение предела функции в точке по Коши
- •Предел функции в бесконечности
- •Точки разрыва функции и их классификация
- •Задачи для самостоятельного решения
- •3. Непрерывность функции в точке
- •4. Производная функции
- •Основные правила дифференцирования
- •Логарифмическое дифференцирование. Производная неявной функции. Производные высших порядков
- •Задачи для самостоятельного решения
- •4. Производная функции
- •5. Правило лопиталя. Дифференциал функции Раскрытие неопределенностей при помощи правила Лопиталя
- •Дифференциал функции
- •Задачи для самостоятельного решения
- •5. Правило Лопиталя. Дифференциал функции
- •6. Исследование функций
- •Общая схема построения графика функции
- •Задачи для самостоятельного решения
- •6. Исследование функций
- •7. Функции нескольких переменных
- •Задачи для самостоятельного решения
- •7. Функции нескольких переменных
- •8. НеоПределенный иНтеграл
- •Основные свойства неопределенного интеграла
- •Основные методы интегрирования а. Непосредственное интегрирование
- •Б. Метод замены переменной (подстановки)
- •В. Метод интегрирования по частям
- •Г. Интегрирование выражений, содержащих квадратный трехчлен
- •Д. Интегрирование простейших рациональных дробей
- •Е. Интегрирование тригонометрических функций
- •Задачи для самостоятельного решения
- •8. Неопределенный интеграл
- •9. ОПределенный иНтеграл
Б. Метод замены переменной (подстановки)
Пусть требуется
вычислить интеграл
![]() ,
который не вычисляется непосредственно.
Сделаем замену переменной
,
который не вычисляется непосредственно.
Сделаем замену переменной
![]() ,
где
,
где
![]() – дифференцируемая функция. Тогда
– дифференцируемая функция. Тогда
![]() и исходный интеграл приобретет вид
и исходный интеграл приобретет вид
![]() .
(1)
.
(1)
Формула (1) называется
формулой
замены переменной в неопределенном
интеграле.
После вычисления интеграла в правой
части этого равенства следует перейти
от новой переменной интегрирования
![]() к старой переменной
к старой переменной
![]() .
.
Пример 3.
Найти интеграл
![]() .
.
Решение.
Сделаем
замену
![]() ,
тогда
,
тогда
![]() ,
а
,
а
![]() .
Найдем
.
Найдем
![]() :
:
![]() .
Следовательно,
.
Следовательно,
![]()
![]() =
=
![]() .
Возвращаясь
к переменной
.
Возвращаясь
к переменной
![]() ,
окончательно получаем:
,
окончательно получаем:
![]() .
.
Пример 4

В. Метод интегрирования по частям
Пусть
![]() и
и
![]() – две дифференцируемые функции. По
свойству дифференциала
– две дифференцируемые функции. По
свойству дифференциала
![]() ,
,
или
![]() .
.
Интегрируя обе
части последнего равенства и учитывая,
что
![]() ,
получаем
,
получаем
![]() .
(2)
.
(2)
Формула (2) называется формулой интегрирования по частям.
В некоторых случаях для нахождения искомого интеграла формулу интегрирования по частям приходится применять несколько раз.
Большая часть интегралов, берущихся по формуле (2), может быть разбита на три группы:
1. К первой группе относятся интегралы вида
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где
![]() – многочлен. Для их вычисления следует
применить формулу (2), полагая в ней
– многочлен. Для их вычисления следует
применить формулу (2), полагая в ней
![]() равным одной из указанных выше функций,
а
равным одной из указанных выше функций,
а
![]() .
.
2. Ко второй группе относятся интегралы вида
![]() ,
,
![]() ,
,
![]() ,
,
где
![]() – многочлен;
– многочлен;
![]() – некоторое число. Для их вычисления
следует положить
– некоторое число. Для их вычисления
следует положить
![]() ,
а
,
а
![]() ,
,
![]() ,
,
![]() соответственно.
соответственно.
3. К третьей группе относятся интегралы вида
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где
![]() и
и
![]() – некоторые числа. Эти интегралы
вычисляются двукратным интегрированием
по частям, причем за
– некоторые числа. Эти интегралы
вычисляются двукратным интегрированием
по частям, причем за
![]() можно принимать любой из сомножителей.
В результате получим уравнение первого
порядка относительно исходного интеграла.
можно принимать любой из сомножителей.
В результате получим уравнение первого
порядка относительно исходного интеграла.
Пример 5

Г. Интегрирование выражений, содержащих квадратный трехчлен
Пусть подынтегральная
функция содержит квадратный трехчлен
![]() .
.
Интегралы вида
![]() вычисляются следующим образом. Из
квадратного трехчлена в знаменателе
выделим полный квадрат:
вычисляются следующим образом. Из
квадратного трехчлена в знаменателе
выделим полный квадрат:

где
![]() ,
если
,
если
![]() ,
и
,
и
![]() ,
если
,
если
![]() .
.
Далее
сделаем подстановку
![]() ,
откуда
,
откуда
![]() ,
,
![]() .
Получим
.
Получим
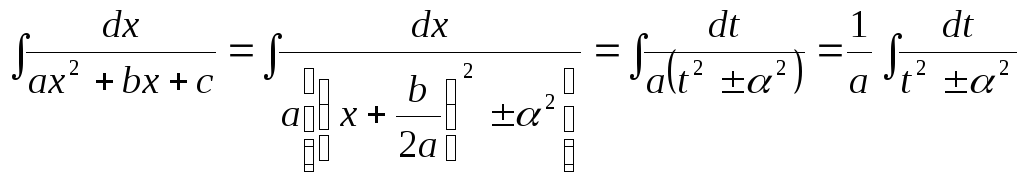 .
.
Последний интеграл является табличным и вычисляется по формулам 15, 16 таблицы основных неопределенных интегралов.
Пример 6.
Вычислить интеграл
![]() .
.
Решение. Выделим в знаменателе полный квадрат:
![]()
![]() .
.
Сделаем подстановку
![]() ,
тогда
,
тогда
![]() и
и
![]()
![]() .
.
Возвращаясь к переменной х, получим
![]() .
.
Д. Интегрирование простейших рациональных дробей
Определение 3.
Рациональной дробью называется дробь
вида
![]() ,
где
,
где
![]() и
и
![]() – многочлены степени
– многочлены степени
![]() и
и
![]() соответственно.
соответственно.
Рациональная дробь
называется правильной,
если степень числителя меньше степени
знаменателя, т.е.
![]() ,
и неправильной
– в противном случае (
,
и неправильной
– в противном случае (![]() ).
).
Неправильная рациональная дробь путем деления многочленов может быть представлена в виде суммы многочлена и правильной рациональной дроби.
Простейшей рациональной дробью называется правильная дробь одного из следующих видов:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() .
.
Интегралы от рациональных дробей 1), 2) находятся методом замены переменной:
![]() [положим
[положим
![]() тогда
тогда
![]() ]
=
]
=
![]()
![]() [возвращаемся
к переменной x]
=
[возвращаемся
к переменной x]
=![]() ;
;
![]() [
[![]()
![]() ]
=
]
=
![]()
![]() [возвращаемся
к переменной x]
=
[возвращаемся
к переменной x]
=![]() .
.
Заметим, что любая правильная рациональная дробь может быть представлена в виде конечной суммы простейших рациональных дробей 1-4, например, методом неопределенных коэффициентов.
Пример 7.
Вычислить интеграл
![]() .
.
Решение.
![]() [сделаем
замену
[сделаем
замену
![]() ] =
] =
![]() .
.
