
- •Примеры:
- •Лемма. Образ и ядро линейного оператора φ являются соответственно подпространствами w и V.
- •Вычисление собственных векторов через главные миноры
- •Билинейные функции.
- •Афинное система координат.
- •Линии и поверхности.
- •Аффинная класификация кривых и поврехностей 2-го порядка.
- •Линейные преобразования унитарного простарнства.
- •Комплексификация евклидова пространства.
- •Ортогональная классификация кривых и поверхностей 2-го порядка.
Афинное система координат.
Пусть V – линейное пространство над полем F (F подполе Q)
Рассмотрим множество
![]() – точки.
– точки.
О. Пусть любой
упорядоченной паре точек поставлен в
соответствие вектор
![]() ²→V
и
²→V
и
-
 А
А

 а
а V
существует единственное B,
что AB=a
V
существует единственное B,
что AB=a -
 А,B,C
А,B,C
 AB+BC=AC
AB+BC=AC
Тогда
![]() наз. афинным пространством, связанное
с линейным пространством V
наз. афинным пространством, связанное
с линейным пространством V
dim![]() =dimV
=dimV
Возьмем O![]()
![]() и назовем ее началом афинной системы
координат.
и назовем ее началом афинной системы
координат.
{O,![]() }
– афинная система координат или
репер.
}
– афинная система координат или
репер.
Аффинными координатами
т. А в аффиной системе координат наз.
набор коэфиициентов разложения
вектора ОА по базису
![]()
Пусть теперь даны
новое начало координат а.с.к O’
и новый базис
![]() .
Q – матрица перехода.
.
Q – матрица перехода.
OO’=![]()
![]()
O’A=![]()
OA=OO’+O’A=![]() [A]
[A]![]() =
=![]() [O’]
[O’]![]() =
=![]() [A]
[A]![]() =
=![]()
[A]![]() =[O’]
=[O’]![]() +Q[A]
+Q[A]![]()
x=c+Qy
y=c’+Q’x – формула афинного преобразования
Аффинное преобразование – это линейное преобразование и сдвиги.
Линии и поверхности.
f(x,y)=0 – уравнение, задающее линию.
f(x,y,z)=0 – уравнение, задающее поверхность.
О. Поверхность называется алгебраической, если f(x,y,z) –многочлен (полином).
Полином - это сумма
мономов:
![]() i,j,k
i,j,k![]() 0
– целые
0
– целые
Степенью монома наз. величина i+j+k. Соответственно степенью полинома наз. максимальная из степеней мономов.
О. Порядок алгебраической поверхности – это стпень полинома f(x,y,z).
Теорема. При аффином преобразовании порядок поверхности не меняется.
Д-во: Применем аффиное преобразование M=C+QM’
Имеем
 Рассмотрим слагаемое полинома моном
Рассмотрим слагаемое полинома моном
![]() .
Применив данное преобразование, мы
получим моном от x’,y’,z’
степени не выше i+j+k.
Поэтому порядок всего полинома не
увеличится. Докажем, что и не уменьшится.
.
Применив данное преобразование, мы
получим моном от x’,y’,z’
степени не выше i+j+k.
Поэтому порядок всего полинома не
увеличится. Докажем, что и не уменьшится.
Применим обратное аффинное преобразование. Порядок полинома не увеличится, а значит при аффинном преобразовании он не может уменьшиться.
Пересечение поверхности с прямой.
Пусть дана поврехность
П k порядка. Рассмотрим
прямую π: x=x![]() +tq.
Подставив в руавнение получим многочлен
от t степени не больше k.
+tq.
Подставив в руавнение получим многочлен
от t степени не больше k.
Ясно, что вщещественных корней не более k, т.е. не более k точек пересечения. Если точек пересчения больше k, то корней больше k. Многчлен степени не больше k имеет больше k корней, отсюда многочлен нулевой.
Т.о. если порядок поверхности k, то либо прямая π целиком содержится, либо она имеет не более k точек пересечения.
Аффинная класификация кривых и поврехностей 2-го порядка.
О. Квадрика –поверхность 2-го порядка.
-
F(x)=x
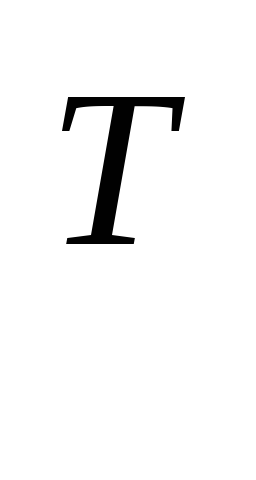 Ax+2a
Ax+2a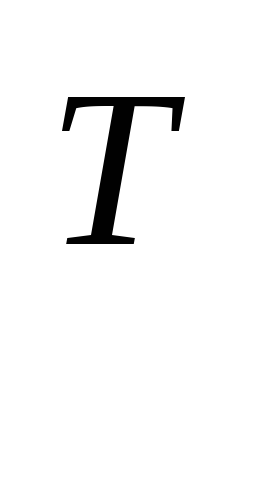 x+α=0
– квадрика
x+α=0
– квадрика
x=![]() A=A
A=A![]()
![]() a=
a=![]() α=a
α=a![]()
Изменение квадрики при аффином преобразовании
-
x=Qy+c (detQ
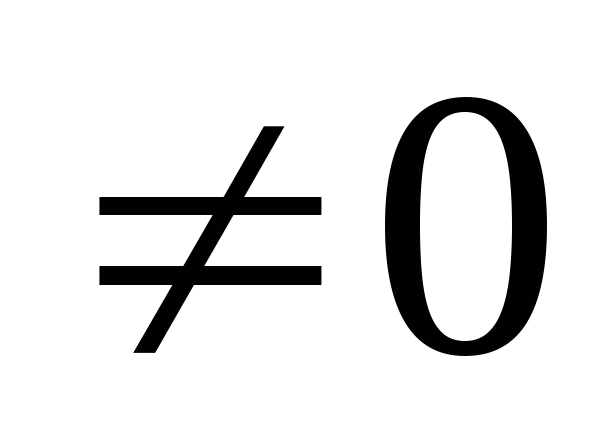 )
=> x
)
=> x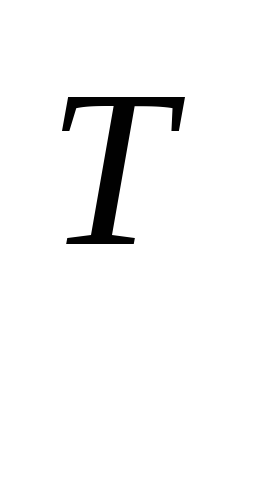 =y
=y Q
Q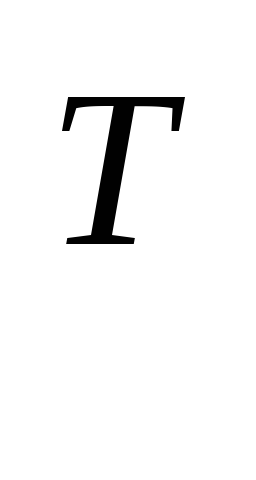 +c
+c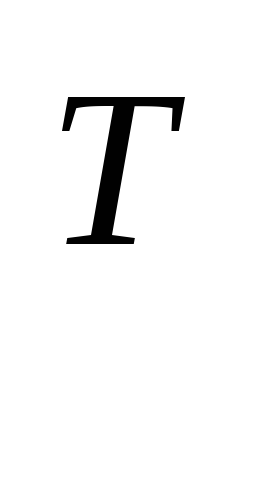
F(y)=(
y![]() Q
Q![]() +c
+c![]() )A(Qy+c)+2a
)A(Qy+c)+2a![]() (Qy+c)+α=0
(Qy+c)+α=0
(3)
F(y)=y![]() By+2b
By+2b![]() y+β=0
y+β=0
F(y)=y![]() Q
Q![]() AQy+y
AQy+y![]() Q
Q![]() Ac+c
Ac+c![]() AQy+2a
AQy+2a![]() Qy+c
Qy+c![]() Ac+2a
Ac+2a![]() c+α=0
c+α=0
y![]() Q
Q![]() Ac=c
Ac=c![]() A
A![]() Qy
(1x1 - число)
Qy
(1x1 - число)
Т.о. B=Q![]() AQ
– конгруэтная матрица
AQ
– конгруэтная матрица
2b![]() =c
=c![]() A
A![]() Q+c
Q+c![]() AQ+2a
AQ+2a![]() Q=2c
Q=2c![]() AQ+2a
AQ+2a![]() Q
=> b=Q
Q
=> b=Q![]() (Ac+a)
(Ac+a)
β=c![]() Ac+2a
Ac+2a![]() c+α
=> β=F(c)
c+α
=> β=F(c)
![]()
![]()
![]()
![]() - расширенные матрицы.
- расширенные матрицы.
Тогда F(x)=![]() =0
(1’). Действительно
=0
(1’). Действительно
![]()
F(y)=![]() (3’), т.к.
(3’), т.к.
![]()
![]() (4)
(4)
Теорема 1. Если
уравнение 1 аффиным преобразованием 2
переходит в уравнение 3, то B=Q![]() AQ,
b=Q
AQ,
b=Q![]() (Ac+a),
β=F(c) или, что тоже самое,
(Ac+a),
β=F(c) или, что тоже самое,
![]() .
.
Д-во: приведено выше
Следствие
1. Матрицы A
и B
и
![]() и
и
![]() - конгруэнтны между собой.
- конгруэнтны между собой.
r(A) – ранг матрицы А. Ранее доказывалось, что r(A)=s(A)+t(A), где s(A) – число положительных коэффициентов в нормальной форме (положительный индекс).
Следствие 2. r(A),
s(A), r(![]() ),
s(
),
s(![]() )
являются аффинными инвариантами
квадрики.
)
являются аффинными инвариантами
квадрики.
Д-во: при аффинном преобразовании ранг матрицы А не меняется, т.к. происходит домножение на невырожденную матрицу Q. По закону инерции для квадратичных форм получаем, что нормальный вид определяется единственным образом, т.е. положительный индекс не меняется. Аналогично доказывается для расширенной матрицы.
Центр квадрики.
-
x=y+c
F(y)=y![]() Ay+2(Ac+a)y+F(c)=0
если Ac+a=0 . то уравнение
квадрики примет вид y
Ay+2(Ac+a)y+F(c)=0
если Ac+a=0 . то уравнение
квадрики примет вид y![]() Ay+F(c)=0
Ay+F(c)=0
Т.о. при переносе начала координат в центр квадрики мы избавляемся от линейных членов уравнения (1).
Ax+a=0
О. Любое решение системы 5 наз. центром квадрики К.
Мы получим,
что если y’![]() K,
то –y’
K,
то –y’![]() K
K
x’=y’+c![]() K
=> x”=-y’+c
K
=> x”=-y’+c![]() K.
K.
Т.о. c – точка симметрии
Лемма. Если квадрика содержит n+1 точек, не лежащих на одной гиперплоскости, тогда из геометрического понимания центра следует алгебраическое понимание центра.
Д-во: Пусть т. c-
точка симметрии, тогда если y![]() +c
+c![]() K,
то -y
K,
то -y![]() +c
+c![]() K
(i=1,..,n+1)
K
(i=1,..,n+1)
Подставляя эти значения
в уравнение (1) и вычтя одно из другого,
мы получим, что а![]() y
y![]() =0
=> a=0, т.к. y
=0
=> a=0, т.к. y![]() n+1 штук. Т.о. система (5) имеет решение.
n+1 штук. Т.о. система (5) имеет решение.
О. Если система 5 несовместна, то квадрика наз. нецентральной.
Лемма. Квадрика
является центральной, если r(![]() )
)![]() r(A)+1,
и нецентральной, если r(
r(A)+1,
и нецентральной, если r(![]() )=r(A)+2.
)=r(A)+2.
Д-во: Квадрика
- центральная => матрица
![]() имеет вид
имеет вид
![]() Поэтому r(
Поэтому r(![]() )
)![]() r(A)+1,
но r(
r(A)+1,
но r(![]() )=r(
)=r(![]() )
)
Квадрика нецентральная =>
О. Рассмотрим случай, когда квадрика содержит какой-нибудь из своих центров. Назовем такую квадрику конической.
Теорема. Любую n-мерную квадрику можно получить из конической n+1-мерной квадрики сечением некоторой гиперплоскостью.
Д-во: Коническая
квадрика имеет вид y![]() Ay=0.
Допустим нам нужно получить квадрику
x
Ay=0.
Допустим нам нужно получить квадрику
x![]() Вx+2b
Вx+2b![]() x+β=0.
Запишем уравнение гиперплоскости в
общем виде q
x+β=0.
Запишем уравнение гиперплоскости в
общем виде q![]() y=γ
y=γ
Нам нужно найти эти q
и γ, чтобы, решив
систему y![]() Ay=0
и q
Ay=0
и q![]() y=γ,
получилось уравнение нужной квадрики.
y=γ,
получилось уравнение нужной квадрики.
Способ 1. (очень плохой)
Зададим
гиперплоскость параметрически
![]() .
.
Т.о. вектор y
будет иметь вид
 .
Подставим его в уравнение конической
квадрики:
.
Подставим его в уравнение конической
квадрики:
y![]() Ay=
Ay=![]() =
=
=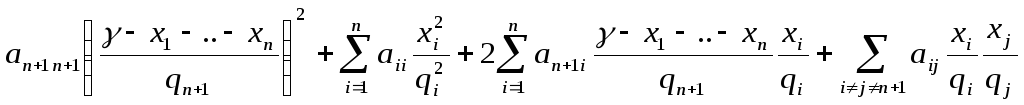 =
x
=
x![]() Вx+2b
Вx+2b![]() x+β
x+β
Отсюда получаем, что, сгруппировав переменные, можно найти коэффициенты в линейной части и квадратичной.
Способ 2. Подставим
y=q![]() x+γ
(x – n-мерный) в уравнение
поверхности:
x+γ
(x – n-мерный) в уравнение
поверхности:
(q![]() x+γ)
x+γ)![]() А(q
А(q![]() x+γ)=(x
x+γ)=(x![]() q+γ
q+γ![]() )A(q
)A(q![]() x+γ)=x
x+γ)=x![]() qAq
qAq![]() x+γ
x+γ![]() Aq
Aq![]() x+x
x+x![]() qAγ+γ
qAγ+γ![]() Aγ=
Aγ=
=x![]() Bx+2b
Bx+2b![]() x+β
x+β
Теорема 2. Для любого уравнения 1 найдется такое аффинное преобразование 2, при котором уравнение 1 перейдет в уравнение 1”
(1”)
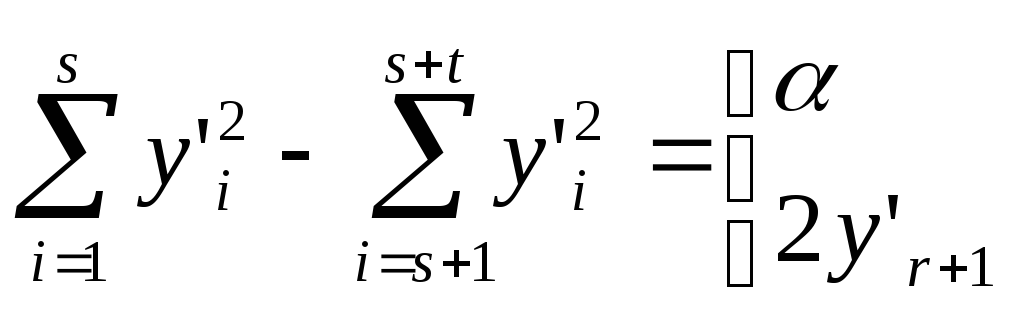
Д-во:
По теореме Лагранжа
существует невырожденная матрица Q,
приводящая матрицу А к нормальному
виду, т.е. Q![]() AQ=diag(1,..,1,-1,..,-1,0,..,0),
где количество 1 – s,
количество –1 – t.
По закону инерции для квадратичных
форм числа r и s
определются единственным образом,
причем r=s+t
AQ=diag(1,..,1,-1,..,-1,0,..,0),
где количество 1 – s,
количество –1 – t.
По закону инерции для квадратичных
форм числа r и s
определются единственным образом,
причем r=s+t
(2) x=Qy (с=0).
Тогда B=Q![]() AQ,
b=Q
AQ,
b=Q![]() a,
β=α
a,
β=α
Имеем
F(y)=![]() =0.
Теперь преобразуем уравнение:
=0.
Теперь преобразуем уравнение:
![]()
Введем новое обозначение
![]()
![]()
 аффинное преобразование
аффинное преобразование
![]()
Если b![]() =0
(i=r+1,..,n), тогда имеем
=0
(i=r+1,..,n), тогда имеем
![]()
Иначе делаем замену
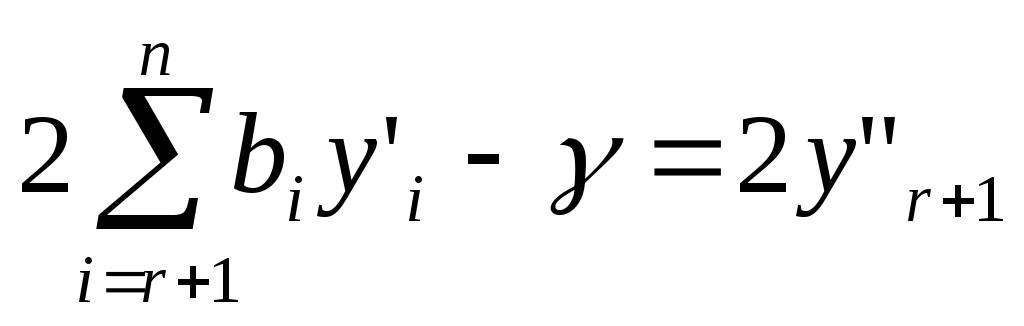 .
В данном случае получаем
.
В данном случае получаем
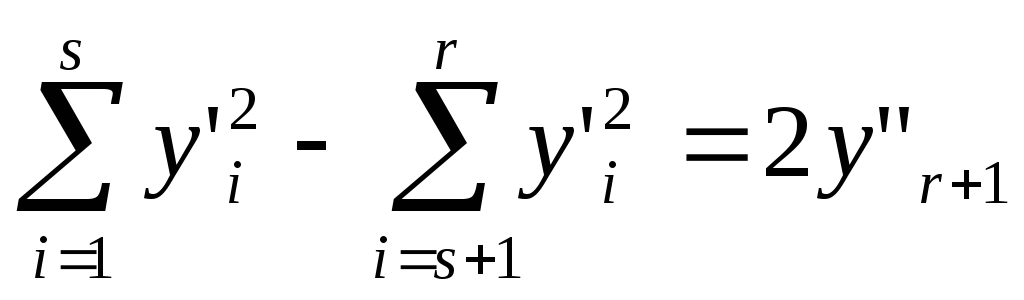 .
.
Лемма. Если F(x)=0,
то λF(x)=0
(λ![]() 0).
И наоборот.
0).
И наоборот.
Т.о. кроме аффинного преобразования можем воспользоваться умножением уравнения на число.
О. Два уравнения квадрики называются аффинно-эквивалентными (1~3), если от одного к другому можно перейти в результате аффинного преобразования (2) или умножения уравнения на произвольное ненулевое число.
Нетрудно показать, что введённое нами отношение аффинной эквивалентности рефлексивно, симметрично и транзитивно. Т.о. ~ есть отношение эквивалентности.
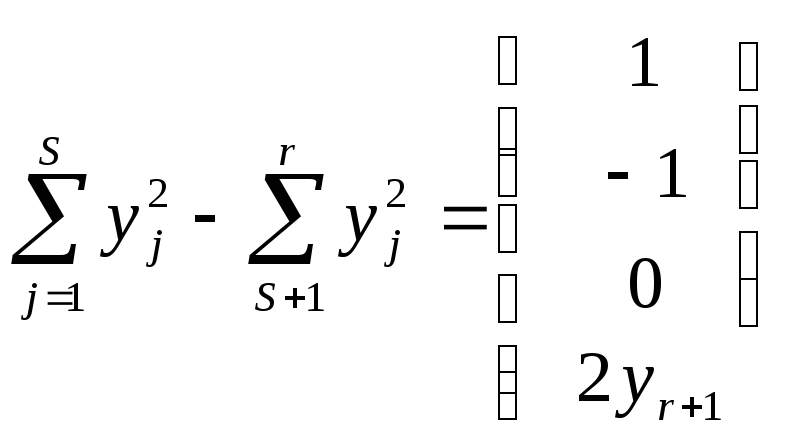
Будем рассматривать
случай s![]() t,
иначе умножим на -1
t,
иначе умножим на -1
Теоерма 2’.
Любое уравнение (1) аффинно эквивалентно
одному из следующих уравнений: если
s>t, то ±1, 0, 2y![]() ,
если s=t, то 1, 0, 2y
,
если s=t, то 1, 0, 2y![]() .
Все эти уравнения аффинно неэквивалентны
между собой.
.
Все эти уравнения аффинно неэквивалентны
между собой.
Д-во: Если s=t
и α=1 и умножим уравнение на –1, тогда
они становятся аффинно эквивалентны.
Если s>t, то все наборы
аффинно неэквивалентны. Если s=t.
То набор будет 1, 0, 2y![]() .
.
Рассмотрим расширенные
матрицы
![]() для каждого из четырёх случаев. Нетрудно
показать, что все эти матрицы попарно
не конгруэнтны, откуда по теореме 1
следует, что уравнение квадрики каждого
из четырёх видов нельзя аффинным
преобразованием привести к другому
виду.
для каждого из четырёх случаев. Нетрудно
показать, что все эти матрицы попарно
не конгруэнтны, откуда по теореме 1
следует, что уравнение квадрики каждого
из четырёх видов нельзя аффинным
преобразованием привести к другому
виду.
-
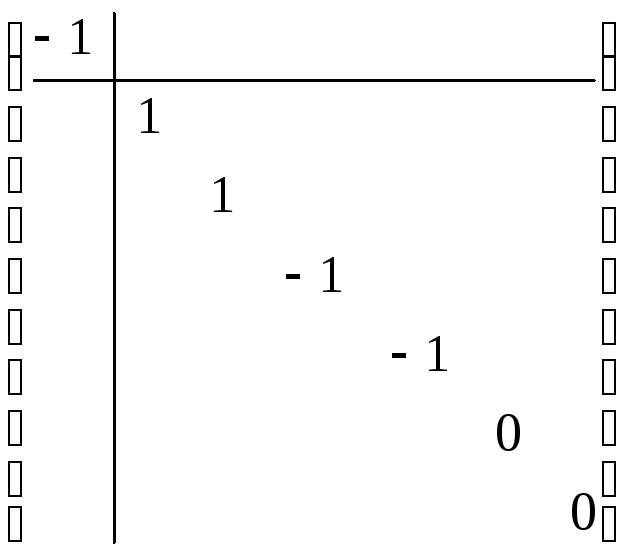 2)
2)
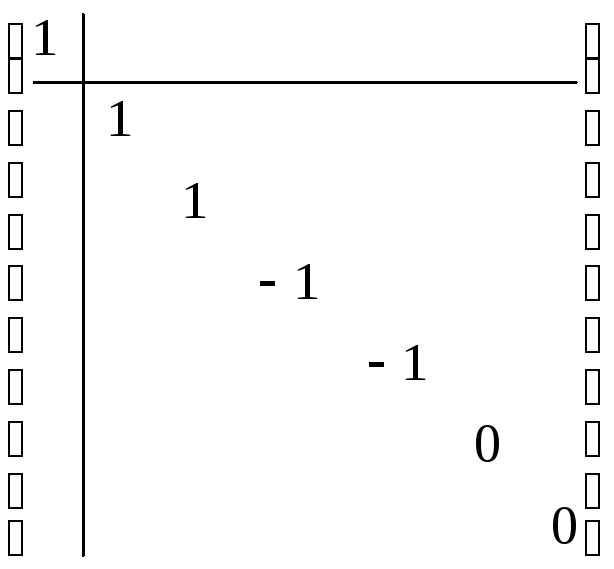 3)
3)
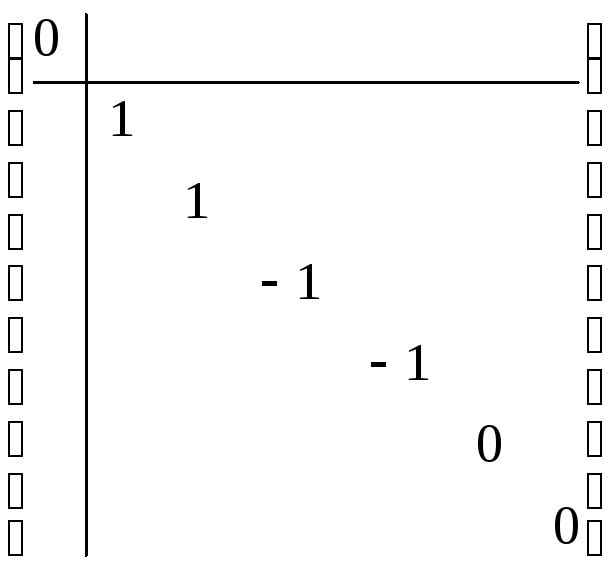
4)
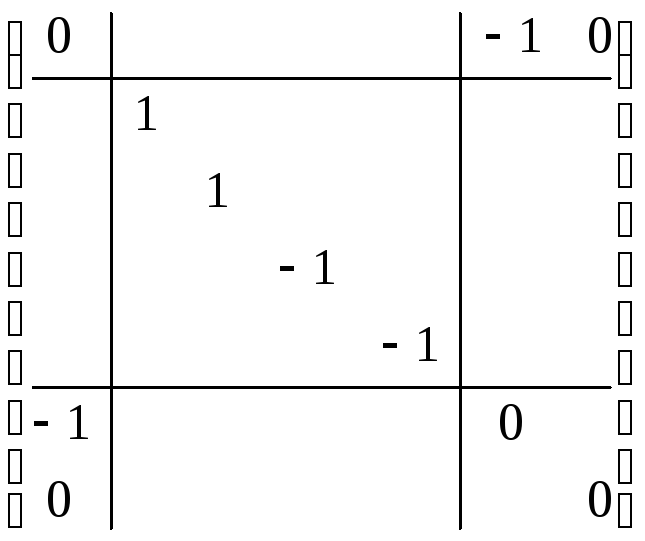
Ранг не меняется – инвариант. Положительный индекс не меняется (инвариант). Везде ранги или положительные индексы разные. Единственность следует из инвариантов.
n = 2
|
Название кривой |
Каноническое уравнение для аффинной классификации |
Расширенная матрица |
r |
S |
|
|
|
Эллипс |
|
diag(–1, 1, 1) |
2 |
2 |
3 |
2 |
|
Мнимый эллипс |
|
diag(1, 1, 1) |
2 |
2 |
3 |
3 |
|
Гипербола |
|
diag(–1, 1, –1) |
2 |
1 |
3 |
1 |
|
Пара мнимых пересекающихся прямых |
|
diag(0, 1, 1) |
2 |
2 |
2 |
2 |
|
Пара пересекающихся прямых |
(x1–x2)(x1+x2)=0 x1=x2, x1=–x2 |
diag(0, 1, –1) |
2 |
1 |
2 |
1 |
|
Парабола |
|
|
1 |
1 |
3 |
2 |
|
Пара параллельных прямых |
|
diag(–1, 1, 0) |
1 |
1 |
2 |
1 |
|
Пара мнимых параллельных прямых |
|
diag(1, 1, 0) |
1 |
1 |
2 |
2 |
|
Пара совпавших параллельных прямых |
|
diag(0, 1, 0) |
1 |
1 |
1 |
1 |
Теорема. Существует ровно 9 аффинно не эквивалентных уравнений, к которым сводится аффинно эквивалентно любое уравнение кривой.
Д-во: Для доказательства
теоремы нам достаточно убедиться в том,
что любую кривую 2-го порядка в
соответствующих аффинных координатах
можно описать одним из перечисленных
канонических уравнений. Так как r=rankB
может принимать лишь два значения
(r=1,2) и 2![]() ,
то матрица В может иметь один из следующих
трёх видов:
,
то матрица В может иметь один из следующих
трёх видов:
![]() или
или
![]() .
Очевидно, приведённая таблица исчерпывает
все возможные варианты расширенных
матриц, соответствующих каждой из трёх
матриц В.
.
Очевидно, приведённая таблица исчерпывает
все возможные варианты расширенных
матриц, соответствующих каждой из трёх
матриц В.
Из этой теоермы вытекает одно интрересное утверждение: при аффинном преобразовании параллельность сохраняется.
Теорема. Существует ровно 17 аффинно неэквивалентных уравнений, к которым сводится аффинно экивалентно любое уравнение поверхности 2-ого порядка.
|
Название кривой |
Каноническое уравнение для аффинной классификации |
Расширенная матрица |
r |
S |
|
|
|
Эллипсоид |
|
diag(–1, 1, 1, 1) |
3 |
3 |
4 |
3 |
|
Мнимый эллипсоид |
|
diag(1, 1, 1,1) |
3 |
3 |
4 |
4 |
|
Однополостный гиперболоид |
|
diag(–1, 1, 1, –1) |
3 |
2 |
4 |
2 |
|
Двуполостный гиперболоид |
|
diag(1, 1, 1, –1) |
3 |
2 |
4 |
3 |
|
Мнимый конус |
|
diag(0, 1, 1, 1) |
3 |
3 |
3 |
3 |
|
Конус |
|
diag(0, 1, 1, –1) |
3 |
2 |
3 |
2 |
|
|
|
0 ……….–1 . …………. . 1 . 1 –1 0 |
2 |
2 |
4 |
3
|
|
Гиперболический параболоид (седло) |
|
0 ……….–1 . …………. . 1 . –1 –1 0 |
2 |
1 |
4 |
2 |
А также цилиндрические поверхности:
Пусть дана некоторая произвольная кривая в пространстве – образующая l и прямая с известным направлением - направляющая а.
Ч ерез
каждую точку образующей l
проведем прямую, параллельную
направляющей а Полученное множество
точек называется цилиндрической
поверхностью, с образующей l
и направляющей а.
ерез
каждую точку образующей l
проведем прямую, параллельную
направляющей а Полученное множество
точек называется цилиндрической
поверхностью, с образующей l
и направляющей а.
Лемма. Уравнение
f(x1,
x2) =
0 задает в трехмерном пространстве
цилиндрическую поверхность с образующей
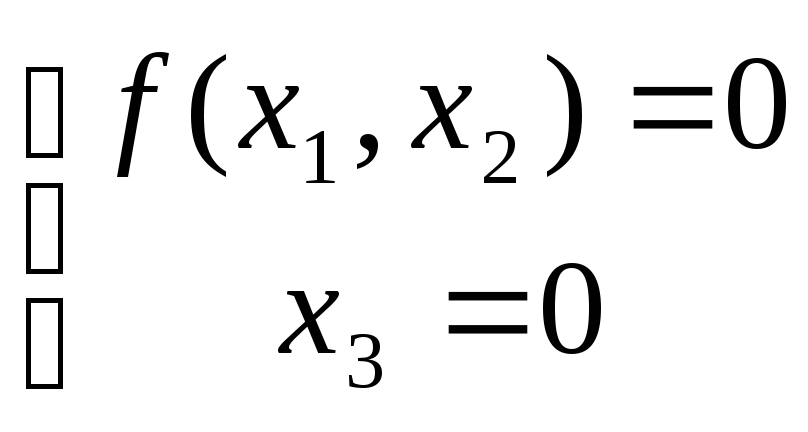 и направляющей Оz.
и направляющей Оz.
Таким образом, 9
поверхностей, канонические уравнения
которых не зависят от координаты
![]() ,
представляют собой цилиндры с образующими,
параллельными оси
,
представляют собой цилиндры с образующими,
параллельными оси
![]() ;
в сечениях этих цилиндров плоскостью
;
в сечениях этих цилиндров плоскостью
![]() лежат соответствующие кривые 2-го
порядка, перечисленные выше.
лежат соответствующие кривые 2-го
порядка, перечисленные выше.
Приведем список цилиндрических поверхностей:
![]() - эллиптический цилиндр;
- эллиптический цилиндр;
![]() - мнимый эллиптический цилиндр;
- мнимый эллиптический цилиндр;
![]() - гиперболический цилиндр;
- гиперболический цилиндр;
![]() - параболический цилиндр;
- параболический цилиндр;
![]() -
пара плоскостей
-
пара плоскостей
![]() ,
пересекающихся по оси
,
пересекающихся по оси
![]() ;
;
![]() -
пара мнимых плоскостей, пересекающихся
по действительной прямой – оси
-
пара мнимых плоскостей, пересекающихся
по действительной прямой – оси
![]() ;
;
![]() -
пара параллельных плоскостей
-
пара параллельных плоскостей
![]() ;
;
![]() -
пара мнимых параллельных плоскостей;
-
пара мнимых параллельных плоскостей;
![]() - пара совпадающих плоскостей
- пара совпадающих плоскостей
![]() .
.
Уравнения оставшихся
поверхностей должны включать все 3
координаты. Переберём варианты строения
матрицы В (с учётом условия
![]() ):
):
1)
 ;
2)
;
2)
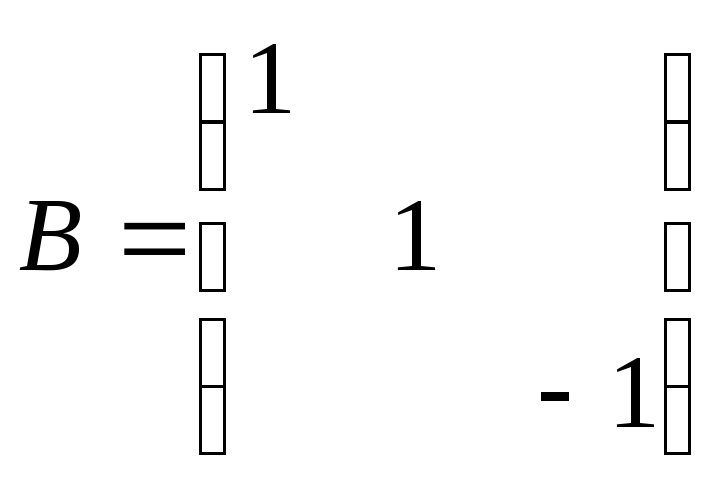 ;
3)
;
3)
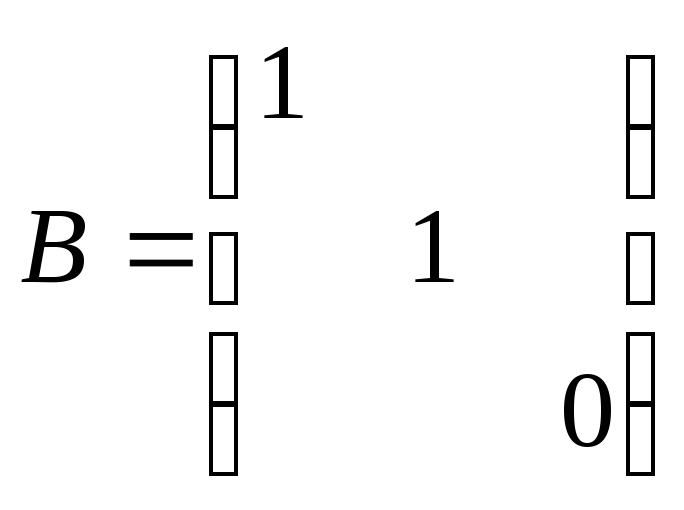 ;
4)
;
4)
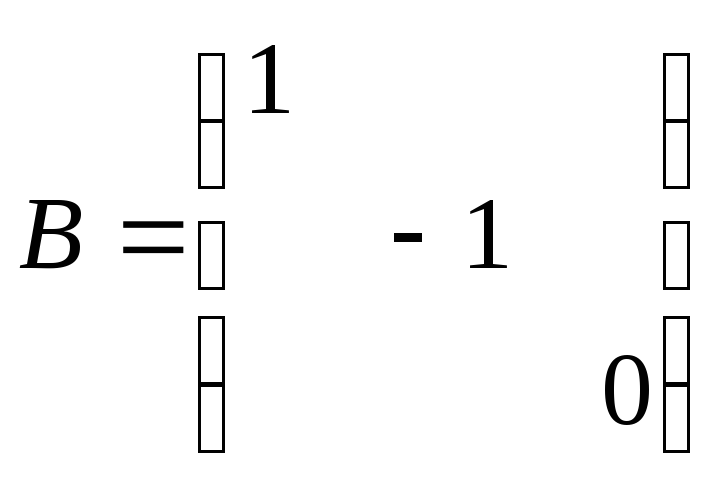 .
.
(В двух последних
случаях необходимо, чтобы расширенная
матрица
![]() содержала ненулевой коэффициент при
переменной
содержала ненулевой коэффициент при
переменной
![]() (иначе получится один из перечисленных
выше цилиндров), следовательно, здесь
получаются нецентральные поверхности).
(иначе получится один из перечисленных
выше цилиндров), следовательно, здесь
получаются нецентральные поверхности).
Поверхность вращения.
Лемма. Пусть x,y,z
- декартова система координат, и
пусть в плоскости y=0
уравнение f(x,z)=0 задает
линию L. Тогда уравнение
![]() задает поверхность вращения,образованную
вращением линии L вокруг
оси Оz.
задает поверхность вращения,образованную
вращением линии L вокруг
оси Оz.
Д-во:
Возьмем точку М(x0,y0,z0),
лежащей на линии L, т.е.
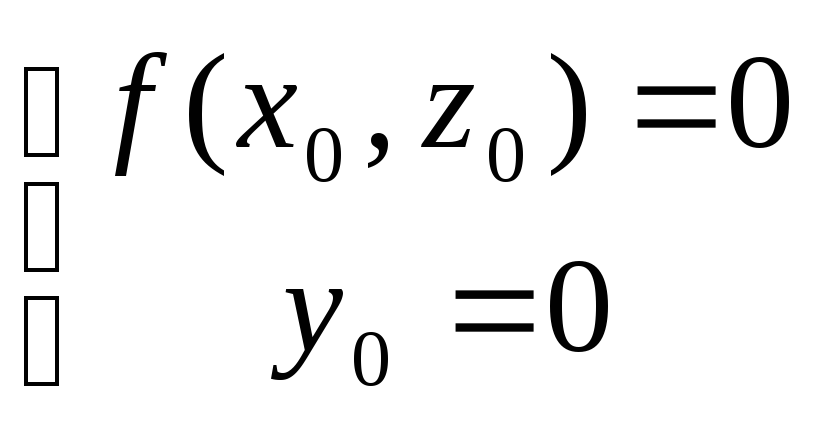
При вращении т.М превращается в окружность, т.е. вместе с т.М искомой поверхности будут удовлетврять все точки лежащие на этой окружности.
Проверим, что все точки удовлетворяют уравнению поверхности:
Расстояние от М до оси
Z:
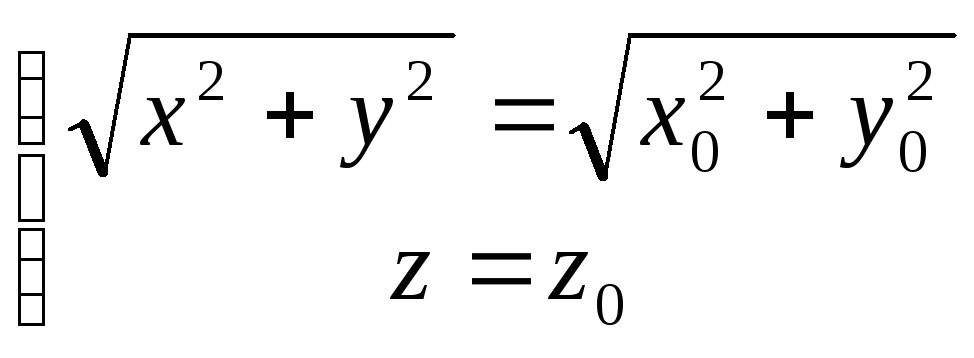
![]()
В обратную сторону:
для любой точки М’
(x’, y’, z’): ![]() найдется на линии L точка,
лежащая на окружности М(x0,y0,z0):
найдется на линии L точка,
лежащая на окружности М(x0,y0,z0):
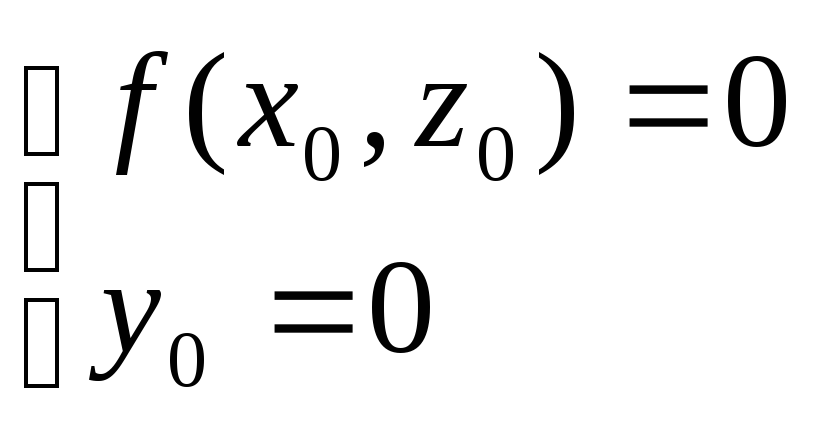
![]() ,
тогда
,
тогда
![]() и
и
![]() .
Доказано
.
Доказано
Асимптотические направления.
π x=x![]() +qt
+qt
(+)
![]() =0
=0
О. Ненулевой вектор
l – называется асимптотическим
направлением относительно уравнения
(1), если
![]() .
.
Если прямая является асимптотическим направлением, то либо прямая целиком лежит в квадрике, либо не имеет точек пересечения, либо точка пересечения одна.
Пересечение прямой и квадрики.
D=(q![]() (Ax
(Ax![]() +a))²-F(x
+a))²-F(x![]() )(q
)(q![]() Aq)
Aq)
С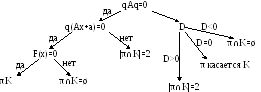 ледствие
1. Для того чтобы прямая
принадлежала квадрики необходимо и
достаточно выполнение трех условий
q
ледствие
1. Для того чтобы прямая
принадлежала квадрики необходимо и
достаточно выполнение трех условий
q![]() Aq=0,
q
Aq=0,
q![]() (Ax
(Ax![]() +a)=0,
F(x
+a)=0,
F(x![]() )=0.
)=0.
О. Отрезок, соединяющий 2 т. пересечения наз. хордой
Следствие 2. Середина
хорды:
![]()
Следствие 3. Прямая
π касается квадрики K в
т. x![]() тогда и только тогда когда
q
тогда и только тогда когда
q![]() Aq
Aq![]() и q
и q![]() (Ax
(Ax![]() +a)=0
+a)=0
Д-во: D=0, но
F(x![]() )=0.
)=0.
Следствие 4. Если
q![]() Aq
Aq![]() ,
x
,
x![]()
![]() K
i=0,..,n, x
K
i=0,..,n, x![]() не лежат в одной гиперплоскости,
тогда среди прямых π
не лежат в одной гиперплоскости,
тогда среди прямых π![]() =x
=x![]() +tq
найдется такая, которая пересекает
квадрику в 2-х точках.
+tq
найдется такая, которая пересекает
квадрику в 2-х точках.
Д-во: Возьмем q![]() =x
=x![]() -x
-x![]() (i=1,..,n) Эти векторы линейно независимы,
тогда q можно по ним
разложить q=
(i=1,..,n) Эти векторы линейно независимы,
тогда q можно по ним
разложить q=![]() ,
причем среди α есть ненулевой.
,
причем среди α есть ненулевой.
Пусть нет такой прямой,
которая пересекала бы К в 2-х точках,
тогда они касаются (q![]() Aq
Aq![]() ).
Т.е. q
).
Т.е. q![]() (Ax
(Ax![]() +a)=0
(i=0,..,n)
+a)=0
(i=0,..,n)
q![]() A(x
A(x![]() -x
-x![]() )=q
)=q![]() Aq
Aq![]() =0
(i=1,..,n) => 0=q
=0
(i=1,..,n) => 0=q![]() A
A![]() =q
=q![]() Aq.
Противоречие.
Aq.
Противоречие.
Следствие 5. q![]() Aq
Aq![]() .
Множество середин хорд, параллельных
направлению q, удовлетворяет
уравнению q
.
Множество середин хорд, параллельных
направлению q, удовлетворяет
уравнению q![]() (Ax+a)=0
(*)
(Ax+a)=0
(*)
Д-во: Возьмем точки xK и xK - концы хорды (она проведена параллельно выбранному направлению), лежащие на квадрике, т.е. F(x)=0, F(x)=0.
Запишем формулу для
середины хорды (![]() ,
,
![]() ,
где t
,
где t![]() ,
t
,
t![]() - различные (D>0) корни
уравнения (+)):
- различные (D>0) корни
уравнения (+)):
![]() ,
где
,
где
![]() находится по формуле Виета:
находится по формуле Виета:
![]() .
Умножим
.
Умножим
![]() на
на
![]() слева:
слева:
![]() => q
=> q![]() (Ax+a)=0.
(Ax+a)=0.
О. Гиперплоскость, определяемая уравнением (*), наз. диаметральной плоскостью, сопряженная не асимптотическому направлению q.
Лемма. Для любой квадрики существует базис из не асимптотических уравнений.
Д-во: Пусть
![]() − аффинная система координат, в которой
квадрика имеет канонический вид. Тогда
можно считать, что матрица квадрики
устроена следующим образом:
− аффинная система координат, в которой
квадрика имеет канонический вид. Тогда
можно считать, что матрица квадрики
устроена следующим образом:

Заметим, что векторы
![]() ,
,
![]() − асимптотические
− асимптотические
![]()
![]() A
A![]() =0.
=0.
Рассмотрим систему
векторов
![]() ,
где
,
где
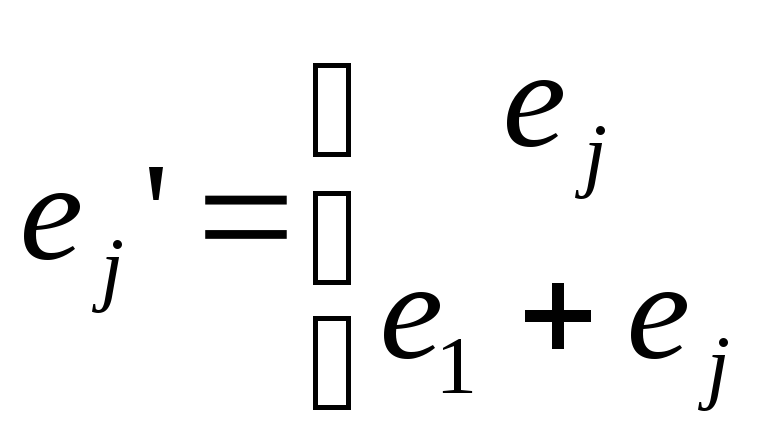
![]()
Очевидно, что
![]() − базис, поскольку матрица перехода
при таком преобразовании будет
невырожденной. Докажем, что все векторы
− базис, поскольку матрица перехода
при таком преобразовании будет
невырожденной. Докажем, что все векторы
![]() ,
,
![]() − не асимптотические относительно
квадрики К. Действительно,
− не асимптотические относительно
квадрики К. Действительно,
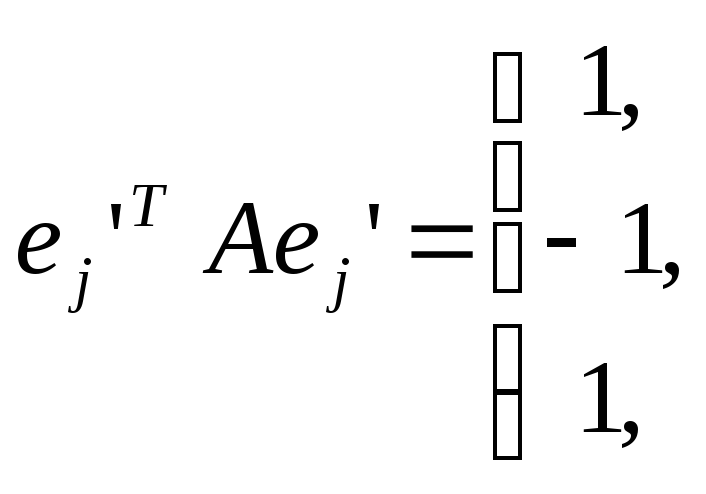

Теорема. Пересечение всех диаметральных гиперплоскостей совпадает с множеством центров квадрики K.
Д-во: Рассмотрим
![]() − базис из не асимптотических направлений
(предыдущая лемма утверждает, что такой
базис всегда существует). Рассмотрим
множество диаметральных гиперплоскостей,
сопряжённых векторам
− базис из не асимптотических направлений
(предыдущая лемма утверждает, что такой
базис всегда существует). Рассмотрим
множество диаметральных гиперплоскостей,
сопряжённых векторам
![]() :
:
![]() .
Так как
.
Так как
![]() − базис, то матрица Q,
составленная из транспонированных
векторов
− базис, то матрица Q,
составленная из транспонированных
векторов
![]() ,
невырожденная.
,
невырожденная.
![]() для всех не асимптотических направлений
квадрики, а так как множество решений
системы уравнений Ax+a=0 совпадает
с множеством центров квадрики, то этим
теорема доказана.
для всех не асимптотических направлений
квадрики, а так как множество решений
системы уравнений Ax+a=0 совпадает
с множеством центров квадрики, то этим
теорема доказана.
Теорема. Через каждую точку одноплостного гиперболоида проходит ровно 2 прямых, лежащих на нем.
Д-во:
![]() .
Отсюда получаем, что (x1
– x3)(x1
+ x3)
= (1 – x2)
(1 + x2)
.
Отсюда получаем, что (x1
– x3)(x1
+ x3)
= (1 – x2)
(1 + x2)
Здесь мы видим целое семейство прямых:
 (x1
+ x3)
= (1
+ x2) (x1
+ x3)
= (1
– x2)
(x1
+ x3)
= (1
+ x2) (x1
+ x3)
= (1
– x2)
(x1 – x3) = (1 – x2) (x1 – x3) = (1 + x2)
2 + 2 0
Легко проверить, что
при![]() получаются
2 различные прямые.
получаются
2 различные прямые.
Теорема. Через каждую точку гиперболического параболоида проходит ровно 2 прямые.
Д-во:
![]() .
Преобразуем уравнение: (x1
– x2)(x1
+ x2)
= 2 x3.
Из этого равенства видно, что
параболоиду принадлежат такие семейства
прямых:
.
Преобразуем уравнение: (x1
– x2)(x1
+ x2)
= 2 x3.
Из этого равенства видно, что
параболоиду принадлежат такие семейства
прямых:
 (x1
+ x2)
= 2
x3 (x1
- x2)
= 2
x3
(x1
+ x2)
= 2
x3 (x1
- x2)
= 2
x3
(x1 – x2) = (x1 + x2) = R
Мы получили 2 различные прямые как и в первом способе.





 Эллиптический
параболоид
Эллиптический
параболоид