
Приложение 4
Таблица преобразований Лапласа
|
№ |
F(p) |
f(t) |
|
1 |
l |
δ(t) |
|
2 |
1/p |
l |
|
3 |
|
|
|
4 |
|
|
|
5 |
|
t |
|
6 |
|
sin at |
|
7 |
|
sh at |
|
8 |
|
|
|
9 |
|
|
|
10 |
|
teat |
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
Приложение 5
Дискретное преобразование Фурье (ДПФ)
Обращение
к цифровым методам обработки сигналов
и ЭЦВМ для производства различных
вычислений требует дискретизации не
только во временной области, но и в
частотной. По аналогии с преобразованием
Фурье (интегральным) применительно к
дискретным функциям разработан
математический аппарат (алгоритм),
называемый дискретным преобразованием
Фурье (ДПФ), который позволяет получить
спектр дискретизированного сигнала
xT(t)
непосредственно по временным выборкам
x(nT) = xn
исходного непрерывного сигнала x(t). ДПФ
формирует спектр дискретизированного
сигнала xT(t)
не в аналоговой (непрерывной) форме, как
![]() ,
а в дискретной. Он представляет собой
совокупность дискретных величин
,
а в дискретной. Он представляет собой
совокупность дискретных величин
![]() на частотах ω = kΩ. Эти компоненты
дискретного спектра
на частотах ω = kΩ. Эти компоненты
дискретного спектра
![]() ,
найденные с помощью ДПФ, совпадают с
соответствующими выборками
,
найденные с помощью ДПФ, совпадают с
соответствующими выборками
![]() непрерывной функции
непрерывной функции
![]() =
=![]() в точках отсчета ω = kΩ; их называют
частотными выборками.
в точках отсчета ω = kΩ; их называют
частотными выборками.
Составим алгоритм ДПФ и ОДПФ (обратное дискретное преобразование Фурье) и найдем условия выбора интервала дискретизации Ω по частоте, а также дадим некоторые рекомендации по подготовке материалов к применению ЭЦВМ для производства вычислений.
Пусть некоторая непрерывная функция времени x(t) дискретизирована
![]() (1)
(1)
и ограничена последовательностью из N отсчетов для 0 ≤ n ≤ N-1, где Т – интервал дискретизации по времени. Дискретный сигнал с ограниченным числом отсчетов (рис.1,а), т.е. конечной длины NT, описывается соответственно конечной суммой
![]() .
(2)
.
(2)
Преобразование Фурье (спектральная функция) такого сигнала
![]() (3)
(3)
является
функцией непрерывной и периодической
с периодом
![]() .
.
Всякая непрерывная функция ST(ω) может быть дискретизирована (по частоте, рис.1,б) подобно дискретизации непрерывной функции x(t) по времени. Для функции (сигнала) x(t) с ограниченным спектром (|ω| ≤ ωв) интервал дискретизации по времени Т находится из условия
![]() ≥
2ωв
или
≥
2ωв
или
![]() , (4)
, (4)
где
Δω = 2ωв
– полная ширина спектра исходного
непрерывного сигнала x(t), другими словами,
протяженность (длина) спектральной
функции
![]() .
Можно сказать, что условия дискретизации
x(t) по времени определяются ее показателями
в частотной области, по ее преобразованию
Фурье F{x(t)}.
.
Можно сказать, что условия дискретизации
x(t) по времени определяются ее показателями
в частотной области, по ее преобразованию
Фурье F{x(t)}.

Рис. 1
Следуя
этому заключению, основанному на
дуальности преобразования Фурье
относительно ω и t, можно сделать вывод,
что интервал дискретизации Ω функции
![]() по частоте будет определяться
протяженностью сигнала во времени
(длиной последовательности) Tc=
NT. Отсюда, пользуясь формулой (4), можем
записать соотношение для определения
интеграла дискретизации по частоте
по частоте будет определяться
протяженностью сигнала во времени
(длиной последовательности) Tc=
NT. Отсюда, пользуясь формулой (4), можем
записать соотношение для определения
интеграла дискретизации по частоте
![]() .
(5)
.
(5)
Относительно
числа отсчетов в частотной области
можно утвержать следующее. Дискретизируемая
функция
![]() -
периодическая с периодом
-
периодическая с периодом
![]() ,
а следовательно, и частотные выборки
,
а следовательно, и частотные выборки
![]() будут повторяться с периодом
будут повторяться с периодом
![]() .
Поэтому достаточно рассмотреть на
периоде
.
Поэтому достаточно рассмотреть на
периоде
![]() конечное число отсчетов. Оно составит
конечное число отсчетов. Оно составит
![]() .
(6)
.
(6)
Таким
образом, если в дискретизированном по
времени сигнале xT(t)
N
отсчетов, то ровно такое же число отсчетов
приходится на период функции
![]() ,
т.е. ее период в N
отсчетов и равен NΩ.
,
т.е. ее период в N
отсчетов и равен NΩ.
Интервал
дискретизации Ω
функции
![]() может быть найден также из представления
дискретной функции конечной длины
x(nT),
0 ≤ n
≤ N-1
дискретным рядом Фурье. Действительно,
если предположить, что дискретная
функция xT(t)
(2) конечной длины в N
отсчетов является периодической с
периодом N(NT),
то она может быть представлена дискретным
рядом Фурье, т.е. суммой дискретных
составляющих (экспоненциальных
может быть найден также из представления
дискретной функции конечной длины
x(nT),
0 ≤ n
≤ N-1
дискретным рядом Фурье. Действительно,
если предположить, что дискретная
функция xT(t)
(2) конечной длины в N
отсчетов является периодической с
периодом N(NT),
то она может быть представлена дискретным
рядом Фурье, т.е. суммой дискретных
составляющих (экспоненциальных
![]() или косинусоидальных и синусоидальных)
с частотами, кратными основной частоте
или косинусоидальных и синусоидальных)
с частотами, кратными основной частоте
![]() периодической последовательности.
периодической последовательности.
Амплитуды
этих составляющих определяются
дискретными значениями
![]() (частотными выборками) спектральной
функции
(частотными выборками) спектральной
функции
![]() ,
найденной по сигналу на периоде, т.е.
x(nT),
0 ≤ n
≤ N-1.
В отличие от ряда Фурье непрерывных
периодических процессов дискретный
ряд Фурье содержит конечное число
экспоненциальных составляющих поскольку
функция
,
найденной по сигналу на периоде, т.е.
x(nT),
0 ≤ n
≤ N-1.
В отличие от ряда Фурье непрерывных
периодических процессов дискретный
ряд Фурье содержит конечное число
экспоненциальных составляющих поскольку
функция
![]() периодична с периодом N.
Следовательно, множество комплексных
экспонент
периодична с периодом N.
Следовательно, множество комплексных
экспонент
![]() с k
= 0, 1, 2, … N-1
определяет все различные комплексные
экспоненты с частотами, кратными
с k
= 0, 1, 2, … N-1
определяет все различные комплексные
экспоненты с частотами, кратными
![]() .
.
Теперь, заменяя в преобразовании Фурье (формула 3) текущее значение частоты ω дискретными значениями kΩ, может записать соотношение для определения частотных выборок
![]() =
=![]() , (7)
, (7)
где k = 0, 1, 2, … N-1.
Это соотношение называется дискретным преобразованием Фурье (ДПФ) функции x(nT).
Для
функций нормированного аргумента x(nT)→
x(n),
![]() →
→![]() формула (7) запишется так:
формула (7) запишется так:
![]() =
=![]() , (8)
, (8)
где k = 0, 1, 2, … N-1.
ДПФ
может давать отсчеты
![]() для k
вне интервала 0 ≤ k
≤ N
–1, но эти отсчеты будут простым
повторением для k,
взятых внутри этого интервала, что
подтверждает непериодический характер
функции
для k
вне интервала 0 ≤ k
≤ N
–1, но эти отсчеты будут простым
повторением для k,
взятых внутри этого интервала, что
подтверждает непериодический характер
функции
![]() .
Ее период составляет N
отсчетов.
.
Ее период составляет N
отсчетов.
Подобно
краткой записи преобразования Фурье
![]() используется краткая запись дискретного
преобразования Фурье
используется краткая запись дискретного
преобразования Фурье
ДПФ{x(nT)}=
![]() ;
ДПФ{x(n)}=
;
ДПФ{x(n)}=
![]() .
.
Существует обратное дискретное преобразование Фурье (ОДПФ), которое переводит ДПФ в последовательность (решетчатую функцию) x(nT), из которой оно было вычислено. Обратное дискретное преобразование Фурье запишется так:
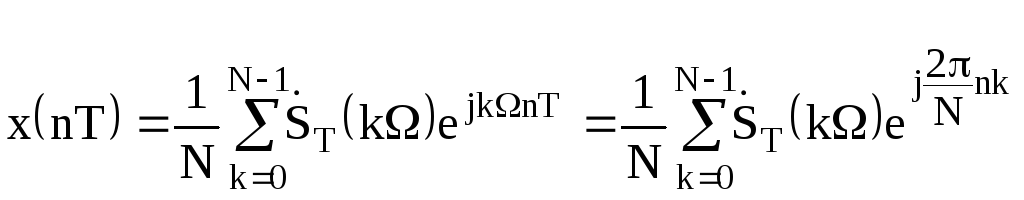 ,
(9)
,
(9)
где n = 0, 1, 2, … N-1;
либо в форме, подобной (8),
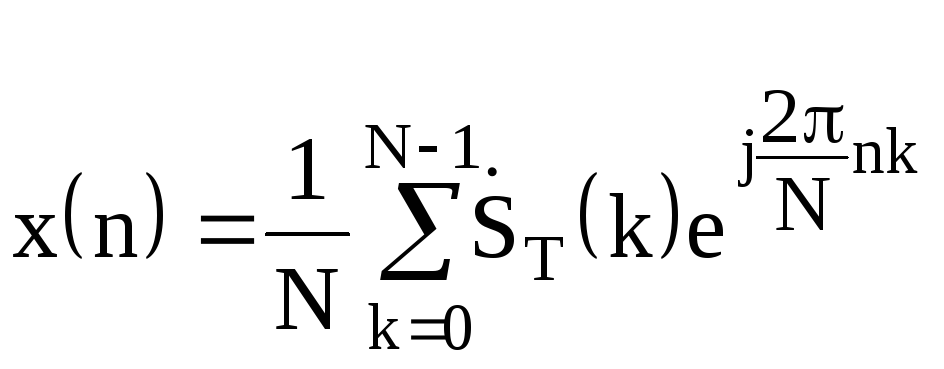 ,
(10)
,
(10)
где n = 0, 1, 2, … N-1.
ОДПФ подобно ДПФ может давать повторяющиеся отсчеты x(nT) для n вне интервала 0 ≤ n ≤ N –1. Ее период также в N отсчетов.
Отметим некоторые свойства ДПФ, играющие важную роль в его практическом применении. Они подобны свойствам преобразования Фурье (теорема о спектрах), рассмотренным выше.
1. Дискретное преобразование Фурье линейно
![]() .
(11)
.
(11)
2. Теорема о сдвиге
![]() (12)
(12)
Сдвиг дискретной функции (последовательности) на целое (m) число отсчетов приводит к изменениям только фазочастотного спектра.
3. Теорема о свертке
![]() .
(13)
.
(13)
ДПФ свертки последовательностей x1(nT), x2(nT) равно произведению ДПФ этих последовательностей.
