ГОСУДАРСТВЕННОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ»

Кафедра «Высшая математика»

ВЫСШАЯ МАТЕМАТИКА

Методические указания к практическим занятиям для студентов дневной и заочной форм обучения всех специальностей, обучающихся по белорусским и российским образовательным стандартам

Матрицы. Системы линейных алгебраических уравнений

Могилёв 2007

УДК 514.742: 514.12

ББК 22.151.5: 22.151.0

B 26

Рекомендовано к опубликованию

учебно-методическим управлением

ГУ ВПО «Белорусско-Российский университет»

Одобрено кафедрой «Высшая математика» «27» декабря 2006 г., протокол № 4

Составители : В. А. Карпенко ; И. У. Примак ;

А. Г. Козлов ; Д. В. Роголев ;

Э. М. Пальчик ; В. Л. Штукарь ;

Н. М. Карпович

Рецензент канд. техн. наук, доц. В. А. Широченко

Выполнены методические разработки практических занятий по теме «Матрицы. Системы линейных алгебраических уравнений» дисциплины «Высшая математика». Методические указания предназначены для студентов дневной и заочной форм обучения всех специальностей, обучающихся по белорусским и российским образовательным стандартам.

Учебное издание

ВЫСШАЯ МАТЕМАТИКА

Ответственный за выпуск Л. В. Плетнёв

Технический редактор А. А. Подошевко

Компьютерная вёрстка В. Э. Ковалевский

Подписано в печать . Формат 60х84/16. Бумага офсетная. Гарнитура Таймс.

Печать трафаретная. Усл. печ. л. . Уч.- изд. л. .Тираж 516 экз. Заказ №

Издатель и полиграфическое исполнение

Государственное учреждение высшего профессионального образования

«Белорусско-Российский университет»

ЛИ №02330/375 от 29.06.2004 г.

212005, Г. Могилёв, пр. Мира, 43

© ГУ ВПО «Белорусско-Российский

университет», 2007

Содержание

1 Операции над матрицами. Определители матриц 4

1.1 Операции над матрицами 4

1.2 Определители матриц 8

1.3 Упражнения 11

1.4 Контрольные задания 12

2 Обратная матрица. Ранг матрицы 13

2.1 Обратная матрица 13

2.2 Ранг матрицы 15

2.3 Упражнения 18

2.4 Контрольные задания 19

3 Невырожденные системы линейных уравнений 20

3.1 Матричный метод решения систем, формулы Крамера 20

3.2 Упражнения 22

3.3 Контрольные задания 23

4 Решение произвольных систем 23

4.1 Основные понятия. Теорема Кронекера-Капелли 23

4.2 Метод Гаусса решения систем линейных уравнений 26

4.3 Упражнения 29

4.4 Контрольные задания 29

5 Однородные и неоднородные системы линейных уравнений 30

5.1 Структура общего решения однородных и неоднородных систем 30

5.2 Упражнения 33

5.3 Контрольные задания 34

Список литературы 34

1 Операции над матрицами. Определители матриц

Цель занятия: усвоение понятий суммы матриц, произведения матрицы на число и произведения матриц, выработка навыков вычисления определителей.

1.1 Операции над матрицами

1.1.1 Определение. Матрицей размера (типа) называется таблица вида

, (1)

состоящая из m строк и n столбцов чисел , , . Числа называются элементами матрицы . Для каждого элемента числа i и j означают номера строки и столбца соответственно, на пересечении которых располагается данный элемент . Кратко пишут: , , . Матрицы и равны, если они имеют одинаковые размеры и для , .

1.1.2 Определение. Матрица , полученная из данной матрицы заменой каждой её строки столбцом с тем же номером, называется транспонированной относительно .

1.1.3 Определение. Суммой матриц и одного и того же размера называется матрица того же размера , элементы которой являются суммами соответствующих элементов и . Краткая запись: .

1.1.4 Определение. Произведением матрицы типа на произвольное число называется матрица типа , элементами которой служат числа , , . Итак, .

Пусть – матрица типа , – матрица типа . Произведением матриц и (в указанном порядке) называется матрица типа , для которой

, , . (2)

Рекомендуем обратить внимание на следующие важные моменты. Суммировать можно только матрицы одного и того же размера. Умножить матрицы и в указанном порядке можно только тогда, когда число столбцов матрицы совпадает с числом строк матрицы . Разность матриц и одного и того же размера естественно определяется так: .

Справедливы следующие свойства операций сложения и умножения матриц (при условии, что они имеют смысл):

, ,

, ,

, ,

, , , (3)

где – единичная матрица типа .

Матрица типа называется квадратной, если , т. е. число строк и столбцов этой матрицы одинаково. Часто говорят, что квадратная матрица имеет порядок .

1.1.5 Определение. Целой положительной степенью квадратной матрицы называется произведение матриц, каждая из которых равна . Нулевой степенью квадратной матрицы называется единичная матрица того же порядка, что и , т.е. .

1.1.6 Определение. Выражение называется многочленом от матрицы .

1.1.7 Пример. Найти матрицу , если

, .

Решение.

Имеем:

.

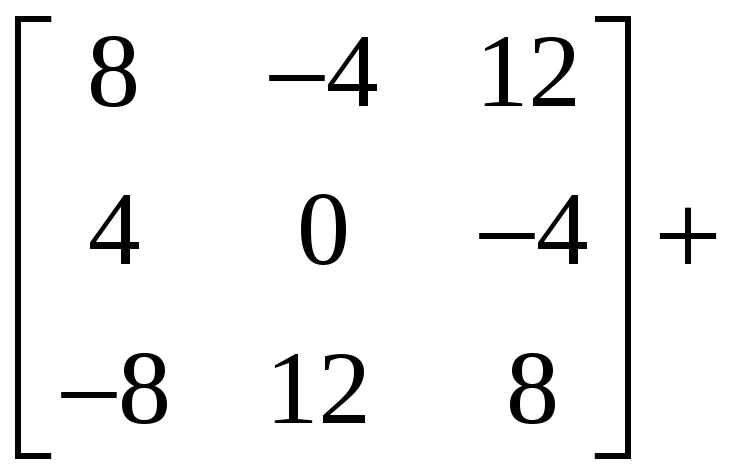
1.1.8 Пример. Вычислить произведение матриц:

, .

Решение.

Матрица имеет размеры , матрица – , поэтому произведение существует и имеет размеры . Вычисляем элементы матрицы по формуле (2):

; ;

; ;

.

1.1.9 Пример. Даны матрицы , , и число . Найти .

Решение.

; ;

; .

1.1.10 Пример. Найти , если , .

Решение.

Матрица .