
- •1. Основные понятия
- •2. Виды интегрируемых нелинейных уравнений п-го порядка
- •2.1. Дифференциальное уравнение вида
- •2.2. Дифференциальное уравнение вида
- •2.3. Дифференциальные уравнения вида
- •2.4. Уравнения, левая часть которого есть точная производная
- •Задания для самостоятельной работы
- •3. Уравнения п-го порядка, допускающие понижения порядка.
- •3.1. Уравнения вида
- •3.2. Уравнение вида
- •3.3. Уравнение, однородное относительно искомой функции и ее производных
- •3.4. Обобщенно однородное дифференциальное уравнение вида
- •3.5. Уравнения, приводимые к виду
- •4.1.2. Неоднородное линейное уравнение
- •4.2. Линейные дифференциальные уравнения с постоянными коэффициентами
- •4.2.1. Однородное уравнение
- •Алгоритм нахождения общего решения однородного линейного уравнения с постоянными коэффициентами
- •4.2.2. Неоднородные линейные уравнения
- •Алгоритм нахождения частного решения уравнения п-го порядка с постоянными коэффициентами методом вариации произвольных постоянных (метод Лагранжа)
- •Алгоритм нахождения частного решения неоднородного линейного уравнения с постоянными коэффициентами методом неопределенных коэффициентов
- •Задания для самостоятельной работы
- •4.3. Линейные дифференциальные уравнения с переменными коэффициентами
- •4.3.1. Уравнения Эйлера
- •Задания для самостоятельной работы
- •4.4. Дифференциальные уравнения второго порядка
- •4.4.1. Приведение уравнения 2-го порядка к каноническому виду
- •4.4.2. Метод исключения из уравнения 2-го порядка слагаемого, содержащего первую производную искомой функции. Уравнение Чебышева
- •Задания для самостоятельной работы
- •4.4.3. Приведение уравнения 2-го порядка к самосопряженному виду
- •4.4.4. Краевая задача для уравнения 2-го порядка
- •Задачи для самостоятельной работы
- •Решение уравнений второго порядка с помощью рядов
- •Задачи для самостоятельной работы
- •Метод малого параметра.
- •Задания для самостоятельной работы
- •Контрольные работы
- •Ответы к заданиям для самостоятельной работы
- •Список использованных источников
4.1.2. Неоднородное линейное уравнение
Для построения общего решения неоднородного линейного уравнения (27)
достаточно найти одно его частное решение у1 и присоединить к нему общее решение
![]() ,
,
соответствующего ему однородного уравнения
![]() .
.
Таким образом, общее решение неоднородного линейного уравнения в области (36) имеет вид:
![]() . (37)
. (37)
Все решения неоднородного линейного уравнения (27) содержатся в формуле (37).
Если правая часть уравнения (27) состоит из нескольких слагаемых
, (38)
то его частное решение будет равно сумме частных решений
![]() (39)
(39)
уравнений с той
же левой частью и правой частью, равной
каждому из слагаемых
![]() в отдельности
в отдельности
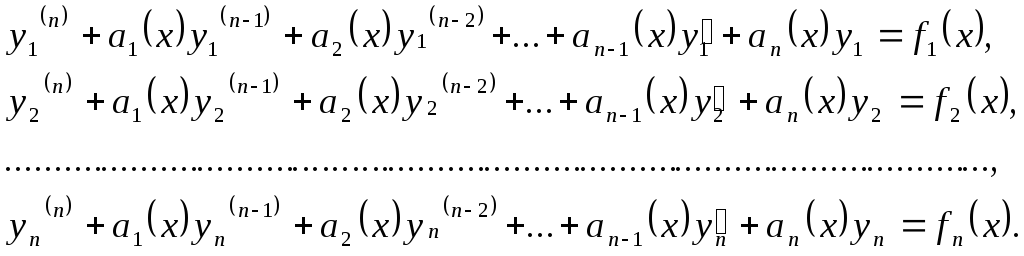
Если известно одно
частное решение
![]() однородного уравнения (27), то можно с
помощью замены
однородного уравнения (27), то можно с
помощью замены
![]() ,
(40)
,
(40)
где z – неизвестная функция, понизить его порядок, а следовательно, и порядок соответствующего ему неоднородного уравнения на единицу. Полученное уравнение (п – 1)-го порядка относительно z также является линейным.
Пример 20.
Найти общее решение уравнения:
![]() ,
если известно одно его частное решение
,
если известно одно его частное решение
![]() .
.
▲ На этот раз, в
отличие от примера 18, воспользуемся
формулой (40). Произведем замену
![]() ;
тогда вычислив производные
;
тогда вычислив производные
и подставив их в исходное уравнение, получим уравнение
![]() .
.
Таким образом, общее решение исходного уравнения будет иметь вид:
,
которое совпадает с выражением общего решения примера 19. ▲
Для нахождения
общего решения неоднородного уравнения
обычно применяют метод
вариации произвольной постоянной
или как его еще называют метод
Лагранжа.
Этот метод показывает, что решение
неоднородного уравнения сводится по
сути дела к решению соответствующего
ему однородного уравнения, т.к. зная
фундаментальную систему решений
![]() однородного уравнения можно найти
частное решение у неоднородного уравнения
в виде:
однородного уравнения можно найти
частное решение у неоднородного уравнения
в виде:
![]() , (41)
, (41)
где - некоторые непрерывно дифференцируемые функции от х, которые необходимо определить. Эти функции можно найти из следующей системы:
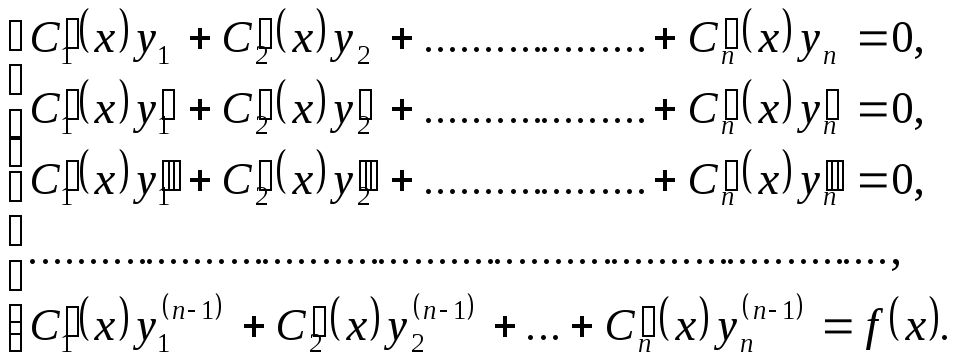 (42)
(42)
Определитель
этой системы представляет собой
определитель Вронского для системы
решений
![]() ,
который отличен от нуля при любом
значении х
из интервала [a,b].
Поэтому
система
(42) дает
единственное решение относительно
при
любом значении х
из интервала [a,b]:
,
который отличен от нуля при любом
значении х
из интервала [a,b].
Поэтому
система
(42) дает
единственное решение относительно
при
любом значении х
из интервала [a,b]:
откуда
![]() .
(43)
.
(43)
Подставляя значения в формулу (41), получим искомое частное решение неоднородного линейного уравнения (27).
Для уравнений второго порядка вида
![]()
система (42) имеет вид
Решение этой системы можно найти по формулам
![]() .
.
Следовательно,
зная выражения для
![]() можно сразу записать вид общего решения
исходного неоднородного уравнения 2-го
порядка:
можно сразу записать вид общего решения
исходного неоднородного уравнения 2-го
порядка:
![]() ,
,
где W(y1, y2) – вронскиан решений y1 и y2 однородного уравнения, соответствующего исходному неоднородному уравнению.
Пример 21. Найти общее решение уравнения:
![]() .
.
▲В примере 19 было найдено общее решение однородного уравнения, соответствующего исходному уравнению
.
Поэтому в соответствии с правилом построения частного решения по методу Лагранжа, представим частное решение исходного уравнения в виде (41)
![]() .
.
Далее составим систему (42)
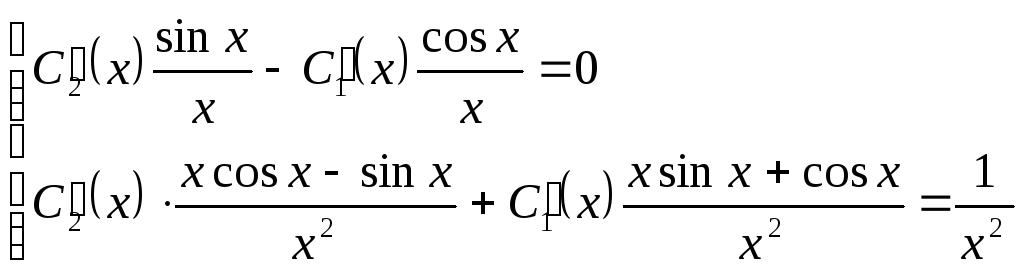 .
.
Разрешая
эту систему относительно
![]() ,
получим
,
получим
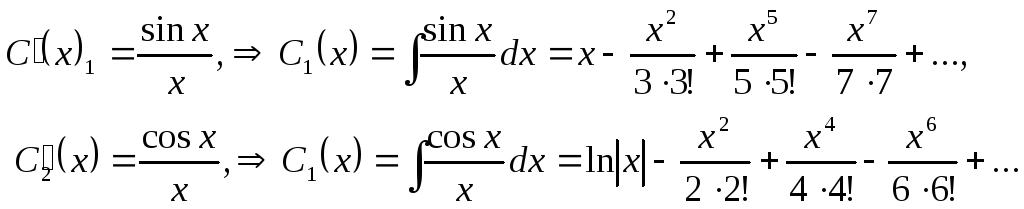
Следовательно, частное решение исходного уравнения будет иметь вид:
![]() .
.
Это же решение можно получить, если использовать формулу
![]() ,
,
с учетом того, что
![]() ,
частное решение имеет вид:
,
частное решение имеет вид:
![]() .▲
.▲
