
2.Взаимное расположение двух плоскостей
Пусть две
плоскости
![]() даны своими общими уравнениями:
даны своими общими уравнениями:
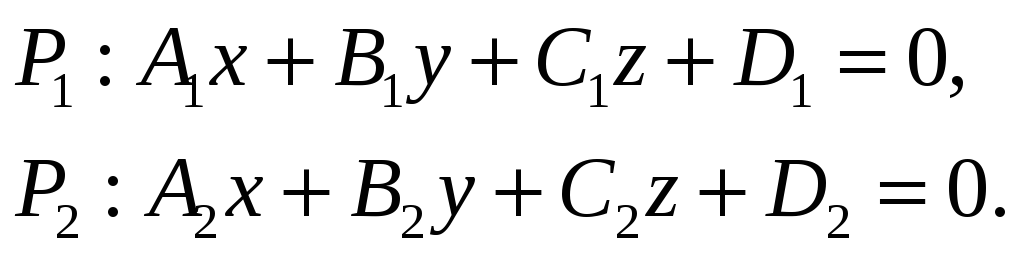
Исследуем
взаимное расположение плоскостей
![]() .
.
1 случай.
Плоскости параллельны, но не совпадают.
В этом случае векторы
![]() должны быть коллинеарны, но плоскости
должны быть различны.
должны быть коллинеарны, но плоскости
должны быть различны.
![]()

![]()



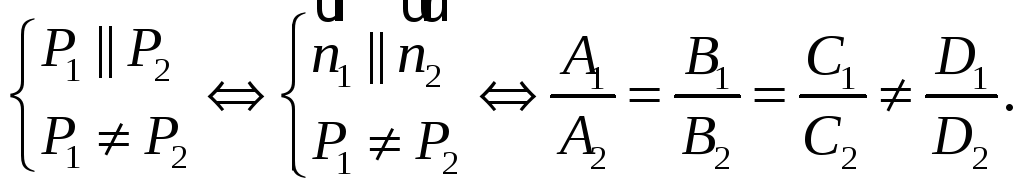
![]()


![]()


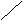

2 случай.
Плоскости совпадают. Векторы
![]() коллинеарны.
коллинеарны.
![]()
3 случай.
Плоскости пересекаются ( по прямой ). В
этом случае векторы
![]() должны быть неколлинеарны.
должны быть неколлинеарны.
![]()

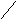
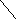
![]()
![]()



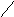






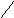
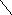



![]()
![]() неверная пропорция.
неверная пропорция.
Очевидно, что в
случае 3 угол между плоскостями равен
углу между нормалями:

Рассмотрим следующую задачу.
Пусть две
плоскости
![]() даны своими общими уравнениями:
даны своими общими уравнениями:
![]()
Необходимо
выписать уравнения плоскостей, делящих
пополам двугранные углы, образованные
при пересечении плоскостей
![]() .
Обозначим искомые плоскости как
.
Обозначим искомые плоскости как
![]()
![]()






![]()








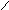

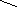




![]()








Обозначим
через
![]() текущую
точку пространства. Точка
текущую
точку пространства. Точка
![]() принадлежит одной из плоскостей
принадлежит одной из плоскостей
![]() тогда и только тогда, когда эта точка
равноудалена от плоскостей
тогда и только тогда, когда эта точка
равноудалена от плоскостей
![]() :
:
![]()
![]()
![]()
![]()
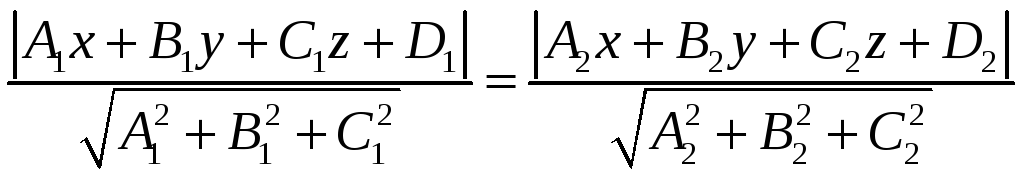
![]()

Выбираем в
последнем соотношении знаки «+» или «-»
в обозначении «![]() »,
получим уравнения плоскостей
»,
получим уравнения плоскостей
![]()
Рассмотрим
три плоскости
![]() ,
заданные своими общими уравнениями:
,
заданные своими общими уравнениями:![]() .
.
Обсудим взаимное
расположение плоскостей
![]()
Очевидно, возможны следующие случаи:
1) Плоскости параллельны (но не совпадают). В этом случае векторы нормалей должны быть коллинеарны:
![]()



![]()
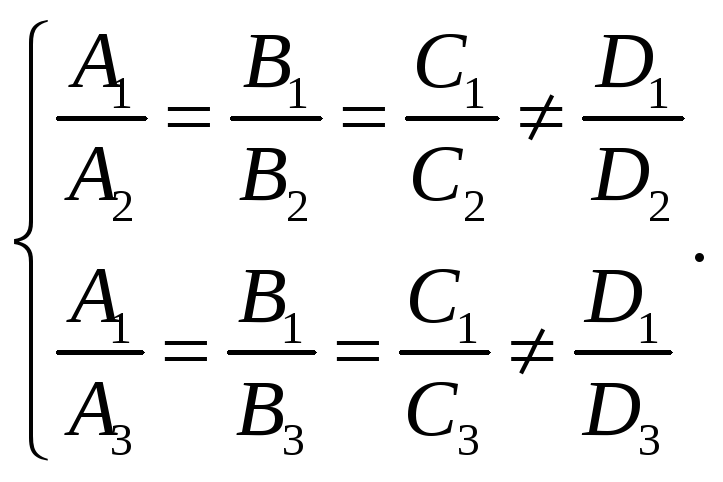
2) Плоскости пересекаются по трем параллельным прямым. В этом случае векторы нормалей должны быть компланарны, но система уравнений, состоящая из общих уравнений плоскостей, должна быть несовместна:
![]()
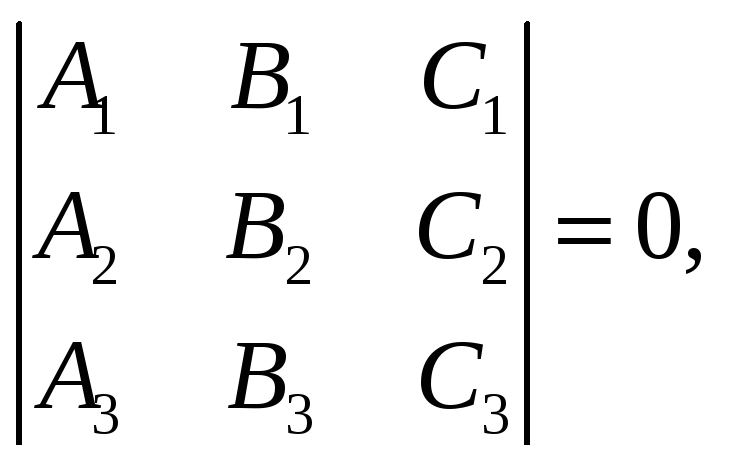
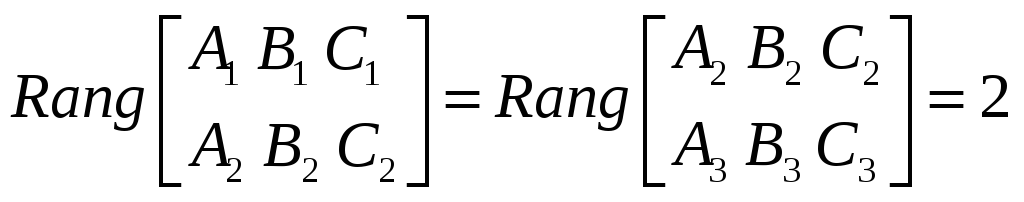 ,
,
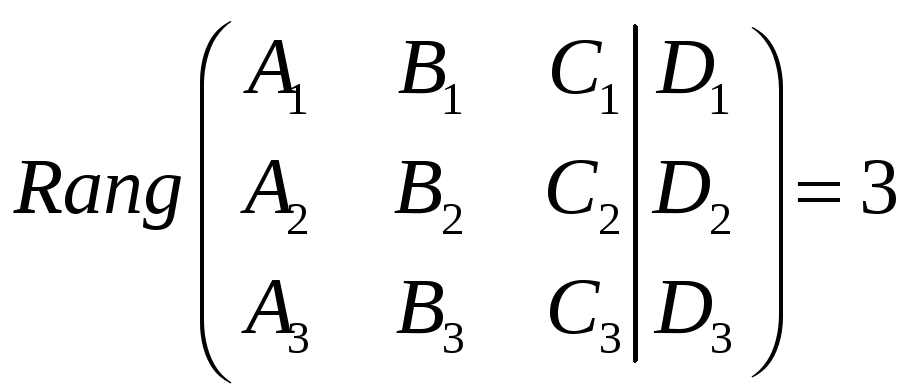


![]()
![]()
![]()

3
![]()


![]()
![]()

Выпишите условия самостоятельно.
4) Три плоскости пересекаются вдоль прямой. В этом случае система, составленная из общих уравнений плоскостей, должна быть совместна, ранг матрицы системы должен быть равен 2. Отсюда получаем:
![]()
![]()

![]()


 .
.
5) Плоскости пересекаются в одной точке. В этом случае система, составленная из общих уравнений плоскостей, должна обладать единственным решением:
![]()
![]()
![]()



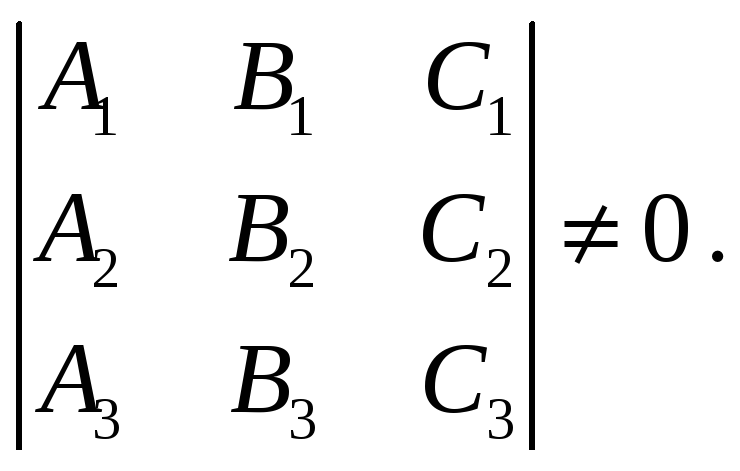
3.Различные уравнения прямой в пространстве
Пусть
![]()
![]() некоторая фиксированная точка
пространства,
некоторая фиксированная точка
пространства,
![]() фиксированный
вектор. Составим уравнение прямой L,
проходящей
через точку
фиксированный
вектор. Составим уравнение прямой L,
проходящей
через точку
![]() параллельно вектору
параллельно вектору
![]() (вектор
(вектор
![]() называется направляющим вектором прямой
L
).
называется направляющим вектором прямой
L
).
M![]() текущую точку пространства. Очевидно,
что точка
текущую точку пространства. Очевидно,
что точка
![]() лежит на прямой
лежит на прямой
![]() тогда и только тогда, когда векторы
тогда и только тогда, когда векторы
![]() и
и
![]() коллинеарны (см.рисунок):
коллинеарны (см.рисунок):
L L L![]()
![]()






Канонические уравнения прямой![]()
![]()
Уравнения (1) называются каноническими уравнениями прямой.
Замечание.
Канонические
уравнения (1) понимаются как пропорции
![]() один или два из знаменателей могу быть
равны нулю.
один или два из знаменателей могу быть
равны нулю.
Пример.
Запишем
уравнение прямой, проходящей через
точку
![]() параллельно оси
параллельно оси
![]() .
.
Имеем:
![]() Отсюда канонические уравнения искомой
прямой имеют вид
Отсюда канонические уравнения искомой
прямой имеют вид
![]() .
.
Перейдем к выводу параметрических уравнений прямой.
Пусть некоторая прямая задана своими каноническими уравнениями:
![]()
Приравниваем
дробь величине
![]() (
(![]()
![]() некоторый параметр,
некоторый параметр,
![]()
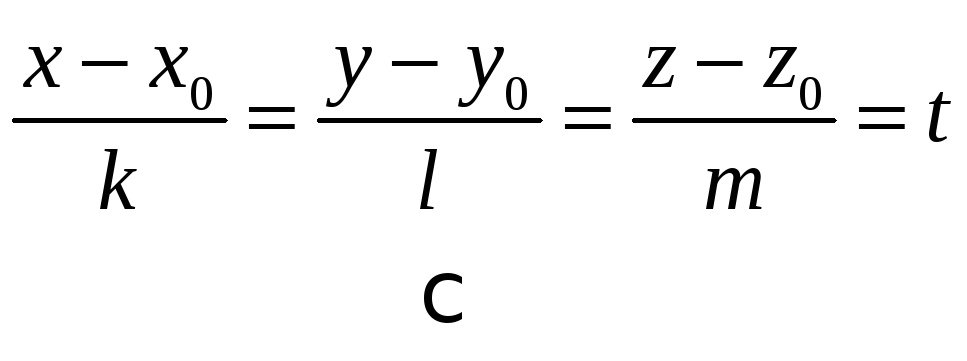
Параметрические уравнения прямой,
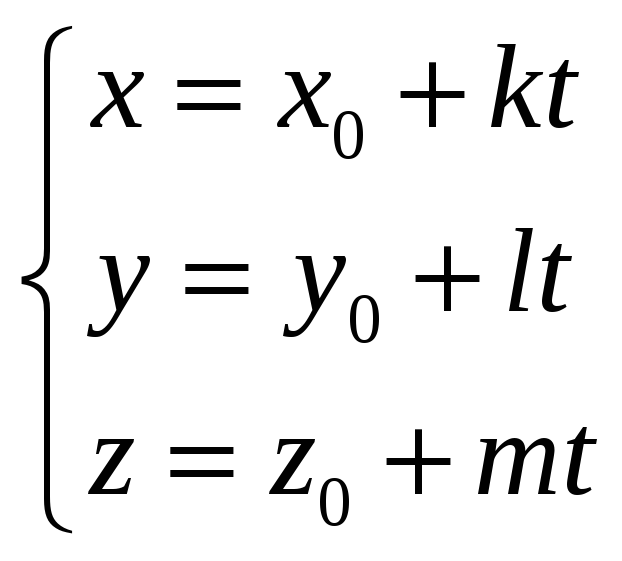
![]()
![]()
(2)
Параметрические уравнения (2) удобно использовать при решении различных задач, например, для нахождения точки пересечения прямой и плоскости.
Пример.
Найдем
координаты точки пересечения прямой
![]() с плоскостью
с плоскостью
![]() :
:
Запишем
параметрические уравнения прямой
![]() :
:
P L A







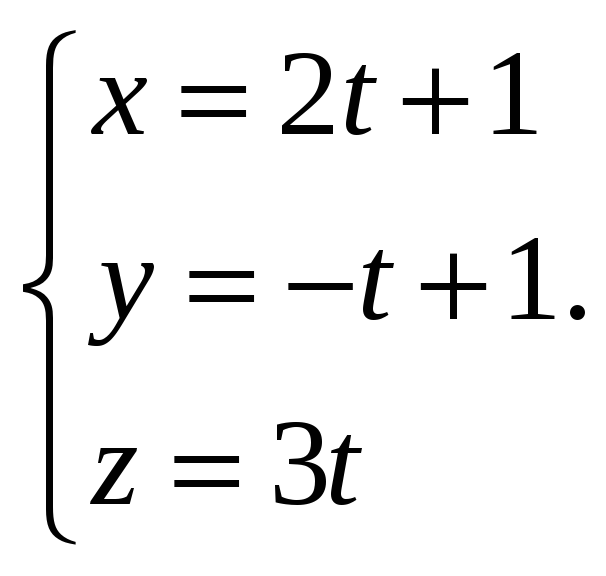
Подставим
правые части этих уравнений в уравнение
плоскости
![]() ,
получим:
,
получим:
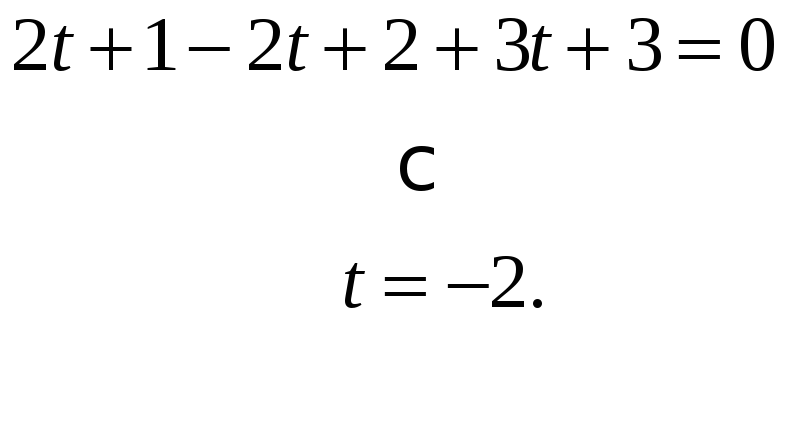
Отсюда точка
пересечения прямой и плоскости имеет
координаты
![]()
Перейдем к
составлению уравнения прямой, проходящей
через две точки
![]() и
и
![]() :
:
![]()
L
![]()
![]()



В качестве
направляющего вектора берём вектор
![]() Обозначим через
Обозначим через
![]() текущую точку пространства. Точка M
принадлежит
искомой прямой тогда и только тогда,
когда векторы
текущую точку пространства. Точка M
принадлежит
искомой прямой тогда и только тогда,
когда векторы
![]() коллинеарны.
коллинеарны.
Тогда канонические
уравнения прямой, проходящей через
точки
![]() имеют вид:
имеют вид:
Уравнения прямой, проходящей через две
фиксированные точки плоскости![]()
![]()
Пример.
Запишем
уравнения прямой, проходящей через
точки
![]() и
и
![]()
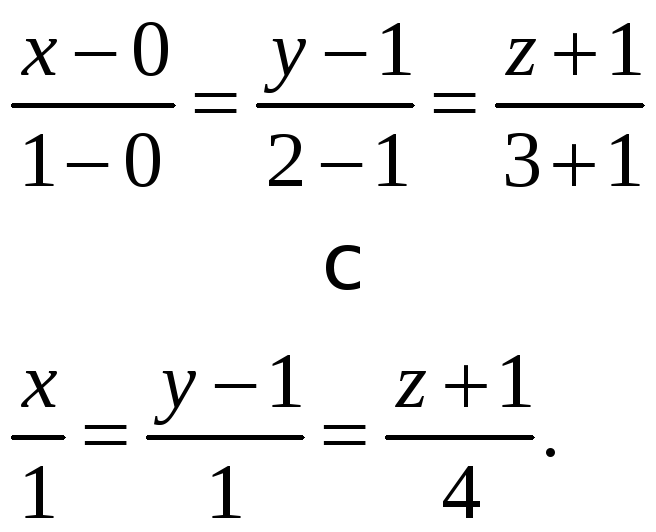
Рассмотрим
две непараллельные плоскости
![]() ,
определенные своими общими уравнениями
( см. рисунок):
,
определенные своими общими уравнениями
( см. рисунок):
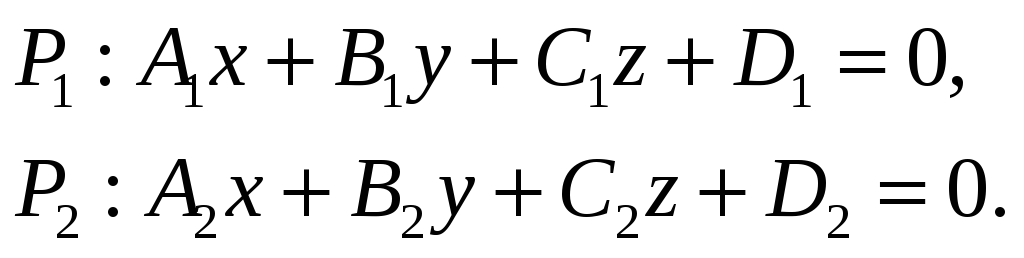
Непараллельные плоскости пересекаются вдоль прямой. Запишем уравнения плоскостей в систему:
Общие уравнения прямой
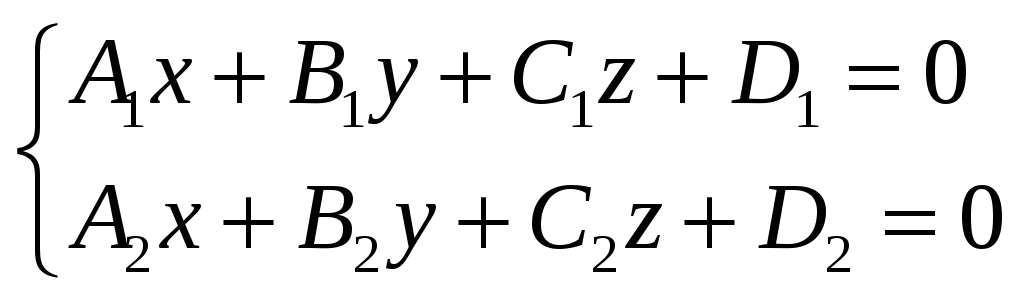
![]()
(4)



![]()






L![]()




Уравнения (4) называются общими уравнениями прямой в пространстве.
Пусть известны общие уравнения прямой L (4). Как получить канонические уравнения этой прямой?
Сначала
найдём координаты точки, лежащей на
прямой L.
Для этого подставим в систему (4), например,
![]() ,
найдём
,
найдём
![]() .
Может случиться, что система (4) при
.
Может случиться, что система (4) при
![]() не имеет решений, тогда подставим
не имеет решений, тогда подставим
![]() или
или
![]() ,
найдем недостающие координаты. Можно
доказать, что обязательно хотя бы один
из вариантов
,
найдем недостающие координаты. Можно
доказать, что обязательно хотя бы один
из вариантов
![]() ,
,
![]() ,
,
![]() позволит найти недостающие координаты
точки, принадлежащей обеим плоскостям.
Фиксируем точку
позволит найти недостающие координаты
точки, принадлежащей обеим плоскостям.
Фиксируем точку
![]() ,
,
![]() .
.
Найдём
направляющий вектор прямой L.
Этот вектор перпендикулярен векторам
![]() ,
следовательно, в качестве вектора
,
следовательно, в качестве вектора
![]() можем взять векторное произведение
векторов
можем взять векторное произведение
векторов
![]() :
:
![]()
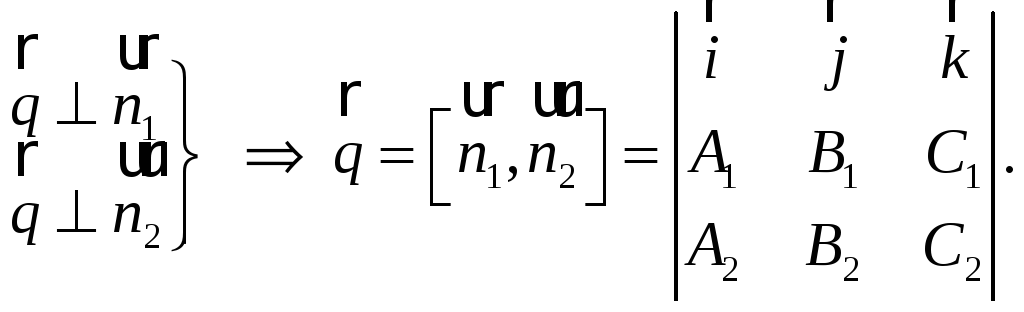
Далее записываем
канонические уравнения прямой L:
![]() .
.
Пример. Прямая L задана общими уравнениями
![]()
Выведем канонические уравнения прямой L.
Пусть
![]() Тогда решаем систему
Тогда решаем систему
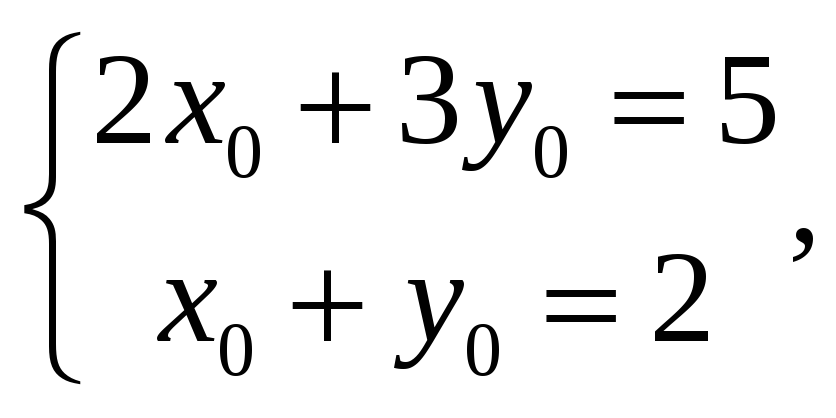
найдем
![]() Получили:
Получили:
![]()
Найдем направляющий вектор:
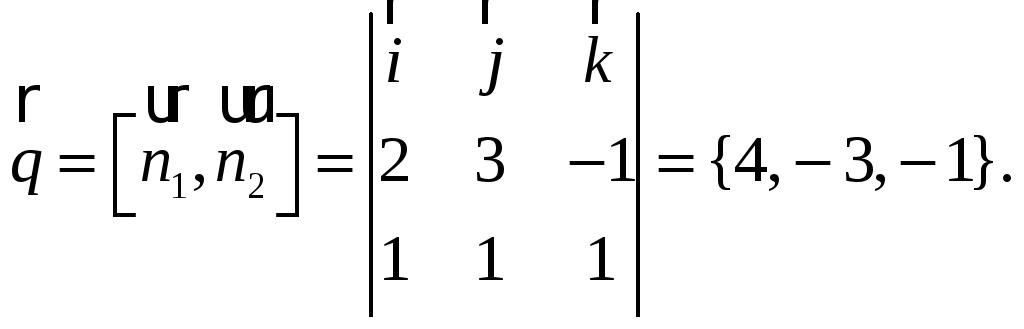
Окончательный ответ:
![]()
