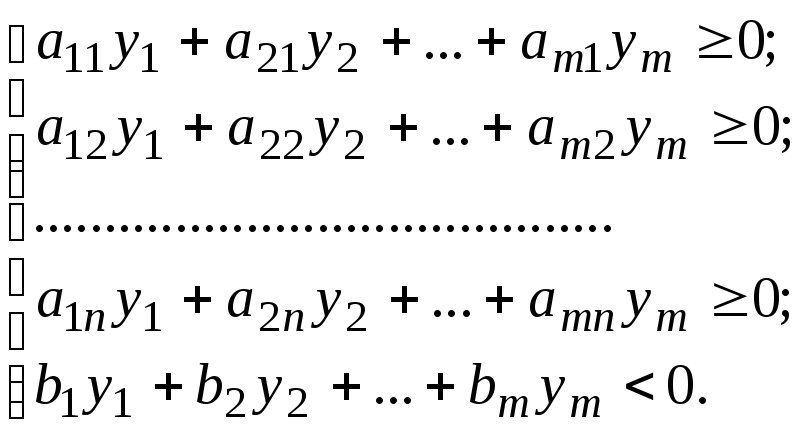- •Міністерство науки і освіти, молоді та спорту України
- •Квадратичні форми.
- •Передмова
- •Лекція 1 Тема: Квадратичні форми План:
- •Алгоритм зведення квадратичної форми до канонічного виду методом Лагранжа.
- •Лекція 2 Тема: Закон інерції квадратичних форм План:
- •Лекція 3 Тема: Ортогональне перетворення квадратичної форми до канонічного виду
- •Лекція 4 Тема: Застосування квадратичних форм до дослідження алгебраїчних рівнянь другого степеня План:
- •Лекція 5 Тема: Квадратична форма в трьохвимірному просторі та її застосування до дослідження рівнянь поверхонь другого порядку План:
- •Лекція 6 Тема: Системи лінійних нерівностей
- •Лекція 7 Тема: Системи лінійних нерівностей
- •Короткий зміст лекції:
- •Система лінійних нерівностей
- •Лекція 8 Тема: Системи лінійних нерівностей План:
- •Лекція 9 Тема: Невід’ємні розв’язки системи лінійних нерівностей План:
- •Лекція 10 Тема: Принцип граничних розв’язків системи лінійних нерівностей План:
- •Лекція 11 Тема: Задачі лінійного програмування План:
- •Лекція 12 Тема: Взаємно двоїсті задачі лінійного програмування
- •Лекція 13 Тема: Симплекс-метод розв’язування канонічної задачі лінійного програмування
- •Контрольні питання для самоперевірки:
- •Лекція 14 Тема: Знаходження невід’ємних розв’язків системи лінійних рівнянь симплекс-методом План:
- •Лекція 15 Тема: Знаходження невід’ємних розв’язків системи лінійних нерівностей симплекс-методом
Лекція 9 Тема: Невід’ємні розв’язки системи лінійних нерівностей План:
-
Теорема Фаркаша.
-
Критерій існування невід’ємних розв’язків системи m лінійних нерівностей з n невідомими.
-
Вузловий мінор.
-
Теорема про існування додатних (від’ємних) розв’язків системи лінійних нерівностей.
Короткий зміст лекції:
Якщо
нерівність
![]() є наслідком сумісної системи
є наслідком сумісної системи
![]() ,
то нерівність
,
то нерівність
![]() є наслідком системи
є наслідком системи
![]() .
.
Нерівність
![]() є наслідком сумісної системи
є наслідком сумісної системи
![]() ,
тоді і тільки тоді, коли нерівність
,
тоді і тільки тоді, коли нерівність
![]() є наслідком системи
є наслідком системи
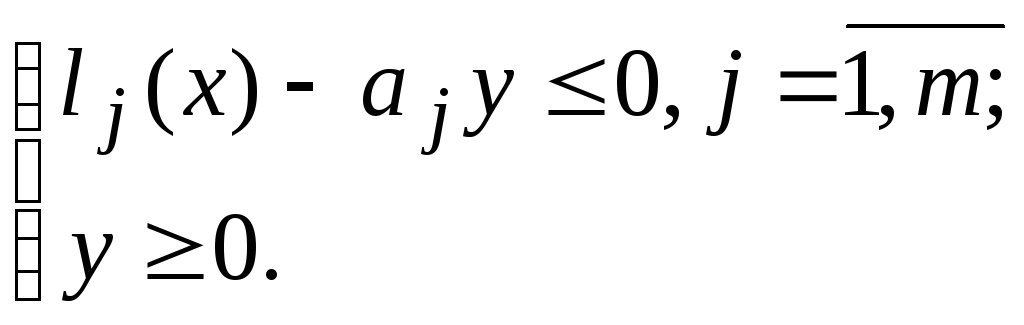
Теорема
Фаркаша.
Якщо нерівність
![]() є наслідком сумісної системи
є наслідком сумісної системи
![]() ,
то існують
,
то існують
![]() ,
для яких стверджується тотожне відносно
,
для яких стверджується тотожне відносно
![]() співвідношення
співвідношення
![]() .
.
З теореми Фаркаша випливає наступна теорема:
Системі лінійних нерівностей
|
|
(1) |
поставимо у відповідність систему
|
|
(2) |
Система лінійних нерівностей (1) має невід’ємний розв’язок тоді і тільки тоді, коли система нерівностей (2) не має невід’ємного розв’язку.
Доведення.
Нехай
система (1) має невід’ємний розв’язок
![]() .
Тоді стверджується нерівність
.
Тоді стверджується нерівність
![]() .
.![]() Покажемо, що система (2) не має невід’ємного
розв’язку.
Покажемо, що система (2) не має невід’ємного
розв’язку.
Припустимо,
що система (2) має невід’ємний розв’язок
![]() .
Тоді справедливі нерівності:
.
Тоді справедливі нерівності:
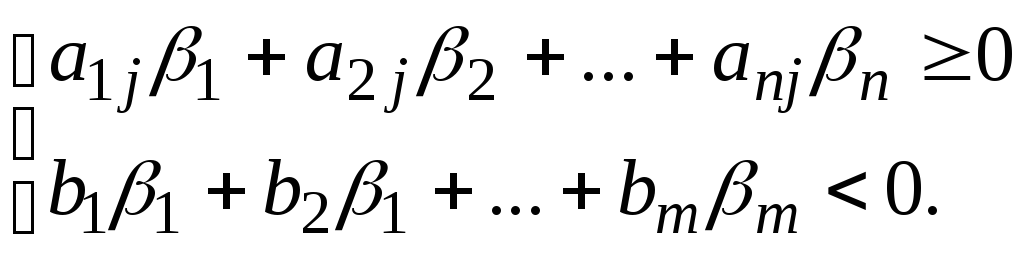
![]()
Оскільки
числа
![]() – невід’ємні, то, з одного боку, з
нерівностей
– невід’ємні, то, з одного боку, з
нерівностей
![]() випливає справедливість нерівності
випливає справедливість нерівності
|
|
(3) |
з
іншого боку, оскільки
![]() –
невід’ємні числа, то з нерівностей
–
невід’ємні числа, то з нерівностей
![]() випливає, що
випливає, що
![]() ,
а тому нерівність (3) не може мати місця.
Отже, припущення, що система (2) має
невід’ємний розв’язок, приводить до
суперечності, а тому воно невірне.
,
а тому нерівність (3) не може мати місця.
Отже, припущення, що система (2) має
невід’ємний розв’язок, приводить до
суперечності, а тому воно невірне.
Припустимо, що система (1) не має невід’ємного розв’язку. Доведемо, що система нерівностей (2) в цьому випадку має невід’ємний розв’язок.
Якщо система нерівностей (1) не має невід’ємного розв’язку, то система рівнянь:
|
|
(4) |
також не має невід’ємного розв’язку, бо якщо ця остання система мала б невід’ємний розв’язок
![]() ,
,
то
система невідомих чисел![]() задовольняла
б системі нерівностей (1).
задовольняла
б системі нерівностей (1).
Оскільки система рівнянь (4) не має невід’ємного розв’язку, то система нерівностей
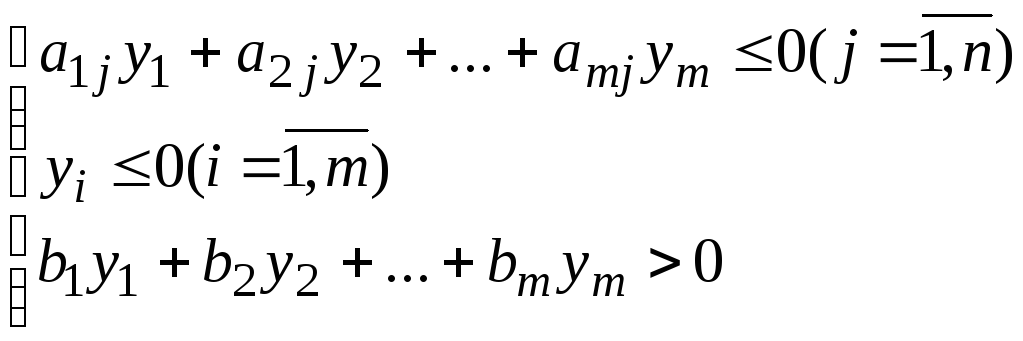
має
деякий розв’язок
![]() .
Але тоді
.
Але тоді
![]() – невід’ємний розв’язок системи
нерівностей
– невід’ємний розв’язок системи
нерівностей
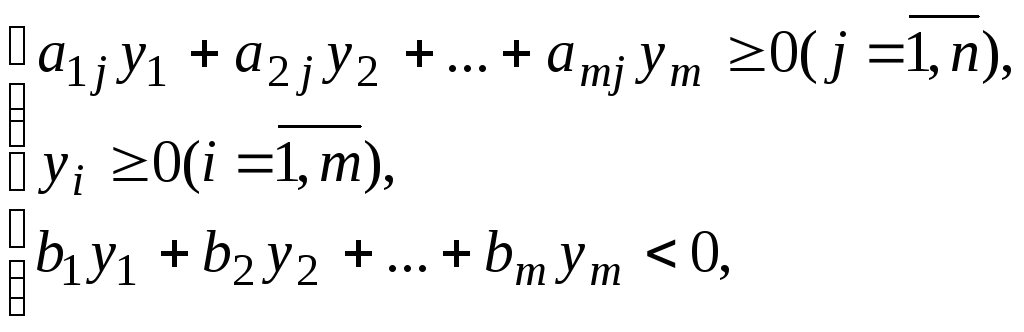
тобто
![]() невід’ємний розв’язок системи
нерівностей (2).
невід’ємний розв’язок системи
нерівностей (2).
Теорему доведено.
Отже, а) або існують невід’ємні розв’язки системи (1) і не існує невід’ємних розв’язків системи (2); б) або існують невід’ємні розв’язки системи (2) і не існує невід’ємних розв’язків системи (1).
Означення.
Відмінний від нуля мінор ∆ матриці А
системи лінійних нерівностей
![]() (відповідно системи лінійних рівнянь
(відповідно системи лінійних рівнянь
![]() )
називається вузловим
мінором
цієї системи, якщо відношення до нього
всіх визначників, одержаним отороченням
його за допомогою довільного рядка
матриці А
і стовпця вільних членів
)
називається вузловим
мінором
цієї системи, якщо відношення до нього
всіх визначників, одержаним отороченням
його за допомогою довільного рядка
матриці А
і стовпця вільних членів
![]() ,
невід’ємне.
,
невід’ємне.
Вузловий
мінор ∆ системи лінійних нерівностей
![]() (відповідно системи лінійних рівнянь
(відповідно системи лінійних рівнянь
![]() )
називається невід’ємно
(недодатно)
орієнтованим,
якщо відношення до нього кожного
визначника, одержаного з нього заміною
деякого стовпця стовпцем вільних членів
)
називається невід’ємно
(недодатно)
орієнтованим,
якщо відношення до нього кожного
визначника, одержаного з нього заміною
деякого стовпця стовпцем вільних членів
![]() ,
невід’ємне (недодатне).
,
невід’ємне (недодатне).
Справедливі наступні теореми:
-
Якщо система лінійних нерівностей
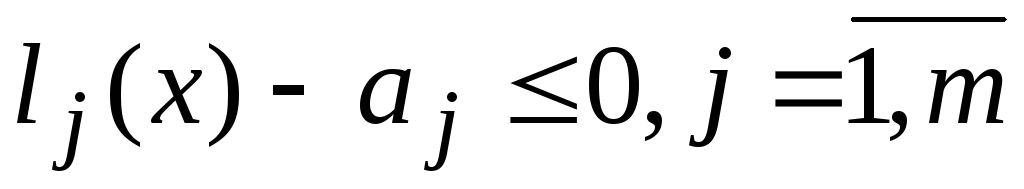 (відповідно система лінійних рівнянь
(відповідно система лінійних рівнянь
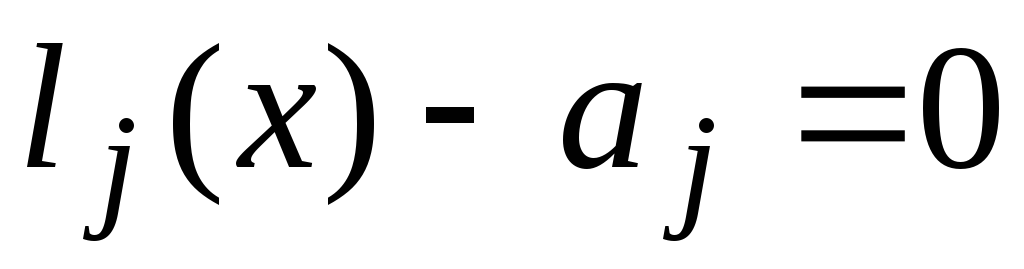 )
рангу r>0
не має нульового розв’язку, то для
того, щоб вона мала додатний (від’ємний)
розв’язок, необхідно і достатньо, щоб
хоч би один мінор матриці системи був
невід’ємно (недодатно) орієнтованим
вузловим мінором цієї системи.
)
рангу r>0
не має нульового розв’язку, то для
того, щоб вона мала додатний (від’ємний)
розв’язок, необхідно і достатньо, щоб
хоч би один мінор матриці системи був
невід’ємно (недодатно) орієнтованим
вузловим мінором цієї системи. -
Щоб система
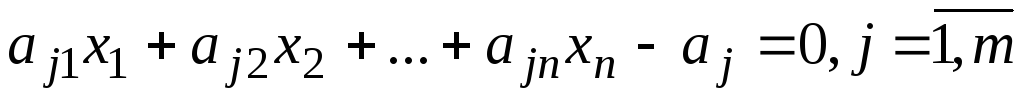 (аналогічно до системи нерівностей
(аналогічно до системи нерівностей
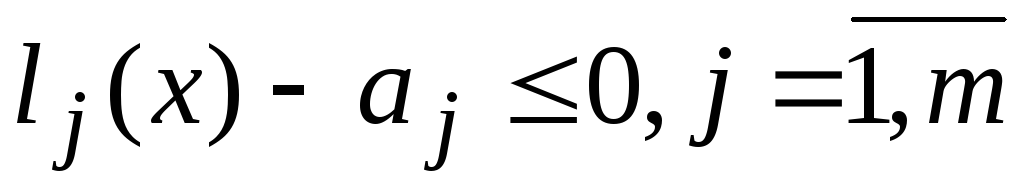 )
мала хоча б один строго додатний
розв’язок, необхідно і достатньо, щоб
система
)
мала хоча б один строго додатний
розв’язок, необхідно і достатньо, щоб
система
 (
(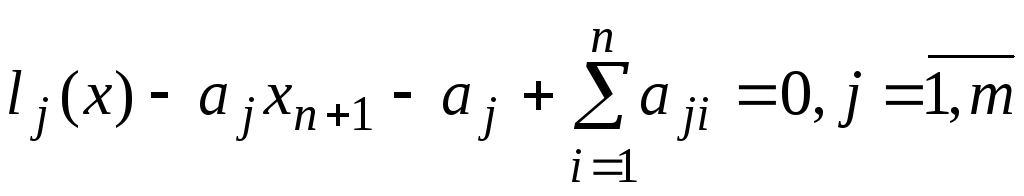 )
мала хоча б один невід’ємний розв’язок.
)
мала хоча б один невід’ємний розв’язок.
Для існування строго від’ємного розв’язку необхідно і достатньо, щоб система
![]()
![]()
мала хоч би один недодатний розв’язок.
Контрольні питання для самоперевірки:
-
Сформулюйте означення наслідку системи лінійних нерівностей
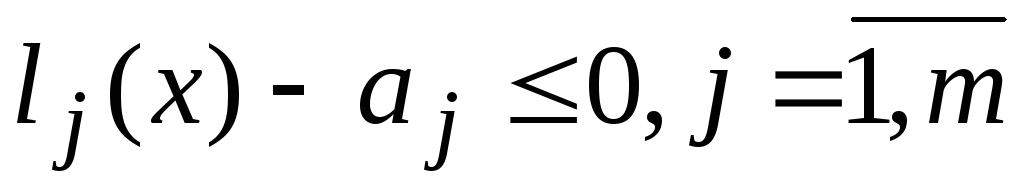 .
. -
Необхідна і достатня умова того, щоб нерівність
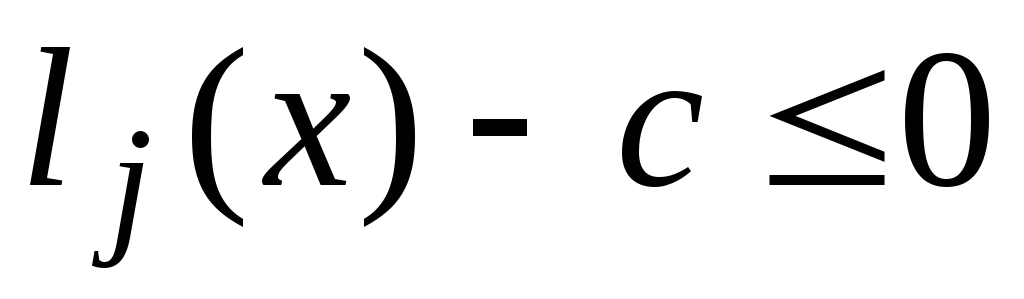 була наслідком сумісної системи
нерівностей
була наслідком сумісної системи
нерівностей
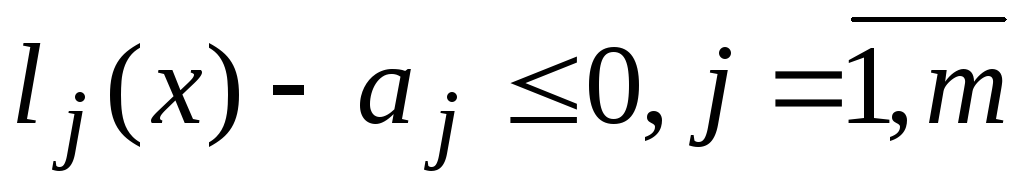 .
. -
Сформулюйте теорему Фаркаша.
-
Доведіть теорему про існування невід’ємних розв’язків системи лінійних нерівностей.
-
Дайте визначення вузлового мінору.
-
Який вузловий мінор називається додатно (від’ємно) орієнтованим?
-
Умови існування додатних (від’ємних) розв’язків системи лінійних нерівностей за допомогою вузлового мінору.
-
З’ясувати, чи має наступна система нерівностей невід’ємні розв’язки::
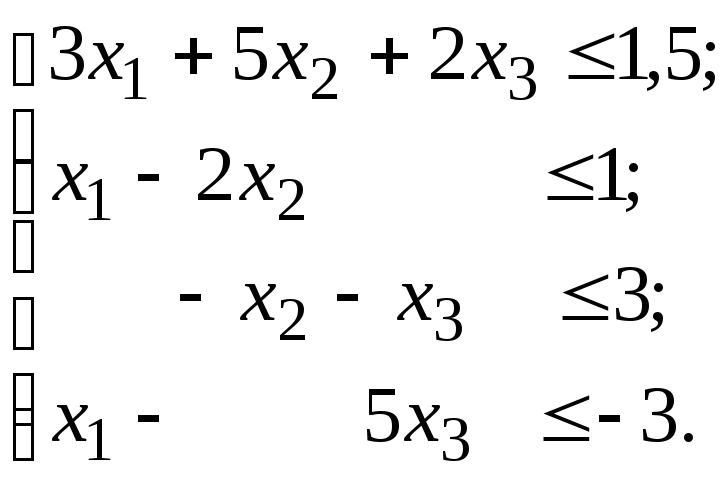
-
Для наступних систем лінійних нерівностей з’ясувати, чи мають вони:
а) додатні розв’язки;
б) від’ємні розв’язки;
в) строго додатні розв’язки;
г) строго від’ємні розв’язки:
-
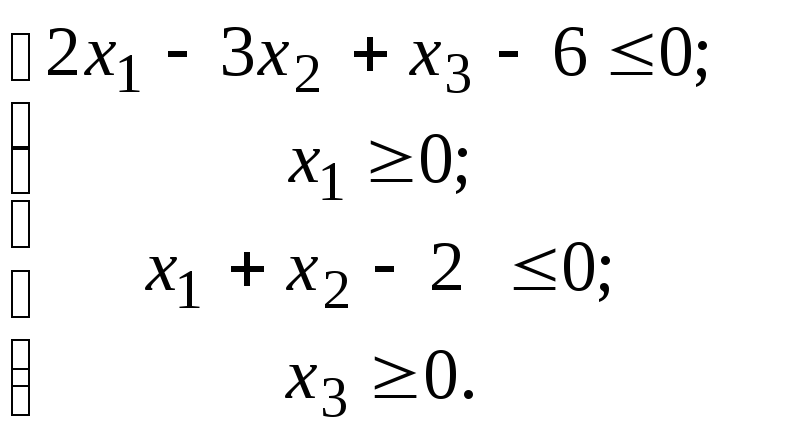 2)
2)
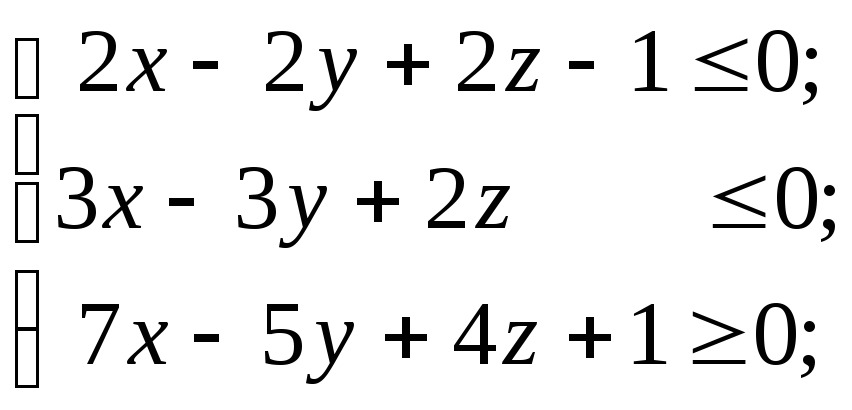
3)
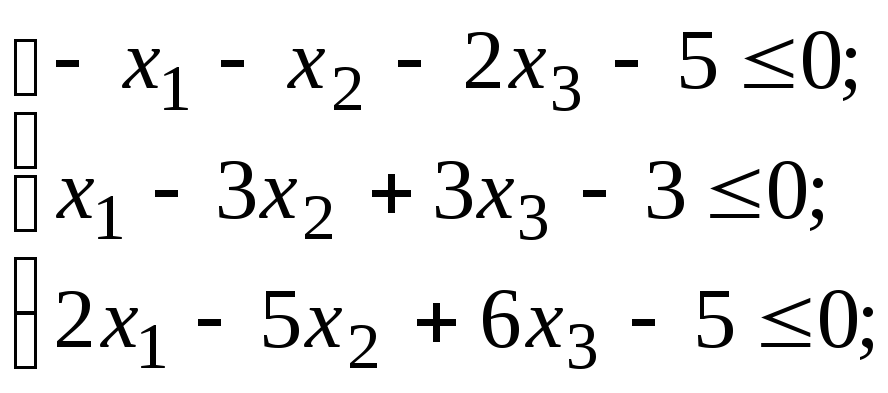 4)
4)

Література:
-
Завало С.Т., Костарчук В.Н., Хацет Б.И. Алгебра и теория чисел, ч. ІІ – К.: Вища шк., 1980. – 402 с., гл. І, §2,4.
-
С.Г. Колесник, В. В. Цыбуленко. Алгебра и теория чисел, ч. ІІ. – Х.: ХГПИ, 1992. – Гл. V, §1,3.