3. Сглаживание кубическими сплайнами

На практике часто вместо интерполяционной таблицы известна таблица экспериментальных данных где, - погрешность, таким образом, вместо значений функции нам известны результаты измерений, содержащие погрешность. Возникают задачи восстановления функции и вычисления производной функции по зашумленным данным. Использование интерполяции в такой ситуации нецелесообразно, т.к. интерполирующая кривая будет существенно зависеть от погрешности (рис. 3.1), а ее производная будет сильно отличаться от (рис. 3.2) /9/.

Если заранее известно, что результаты измерений содержат погрешности , то естественно рассматривать не задачу интерполяции, а задачу сглаживания, т.е. задачу построения гладкой (непрерывно дифференцируемой, дважды непрерывно дифференцируемой) функции, которая проходила бы не через заданные точки а вблизи них. На рис. 3.1 /9/ приведен график функции на отрезке точками отмечены результаты измерений выведена интерполяционная кривая и сглаживающая кривая (пунктиром). На рис. 3.2 /9/ приведены графики производной на отрезке производной интерполяционной кривой и производной сглаживающей кривой (пунктиром).

Рекомендуемая литература: /1, 4, 9/.

3.1. Постановка задачи сглаживания

В литературе приводятся различные формулировки постановки задачи сглаживания. Приведем две из них.

1. Пусть на отрезке задана таблица , где погрешность.

Требуется построить гладкую функцию , которая достаточно близка к функции на отрезке .

2. Пусть на отрезке задана таблица , где погрешность, и положительные числа Требуется построить гладкую функцию , такую что

Задача сглаживания заключается в восстановлении гладкой функции по зашумленным табличным данным. Понятно, что эта задача, как и задача интерполяции, имеет множество решений. Накладывая определенные ограничения на функцию , получаем задачу, имеющую единственное решение. На практике для решения задачи сглаживания чаще всего используются сглаживающие кубические сплайны. Мы рассмотрим естественный сглаживающий кубический сплайн (остальные сглаживающие кубические сплайны отличаются от него краевыми условиями).

Определение естественного сглаживающего кубического сплайна

Пусть на отрезке задана сетка в узлах которой заданы значения Естественным сглаживающим кубическим сплайном называется функция , удовлетворяющая следующим условиям:

1. функция 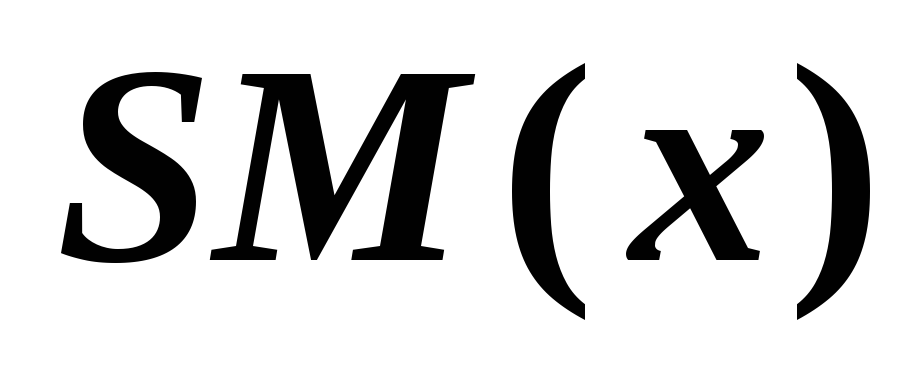- дважды непрерывно дифференцируемая функция на

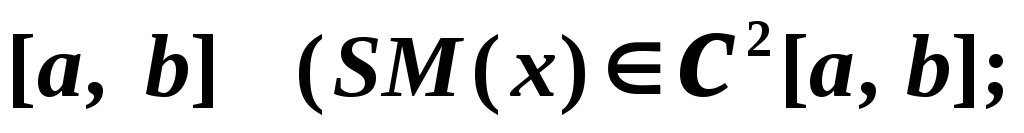
2. на каждом из отрезков 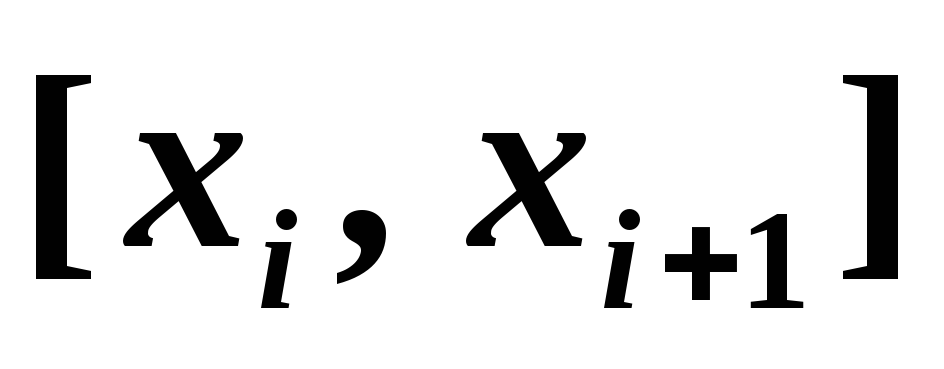функция 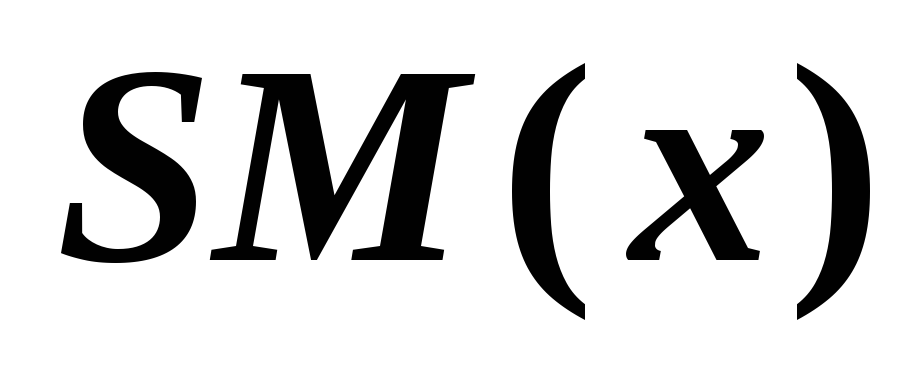является полиномом третьей степени вида

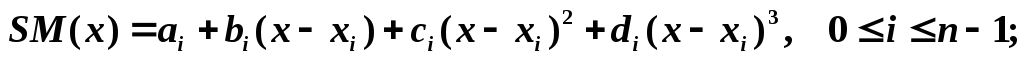
3. функция 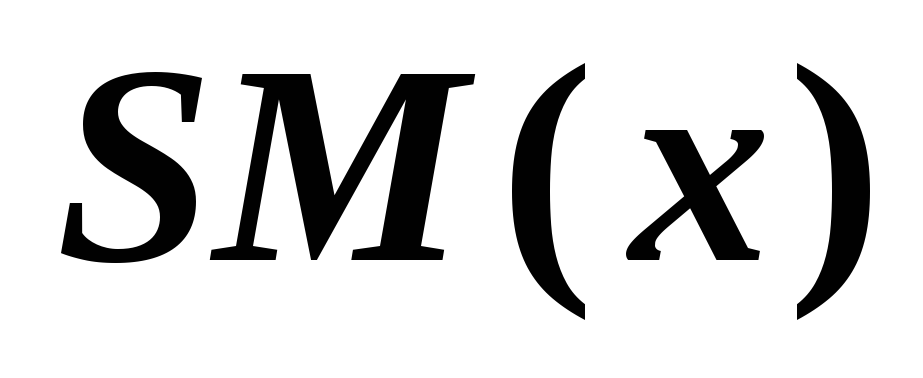доставляет минимум функционалу 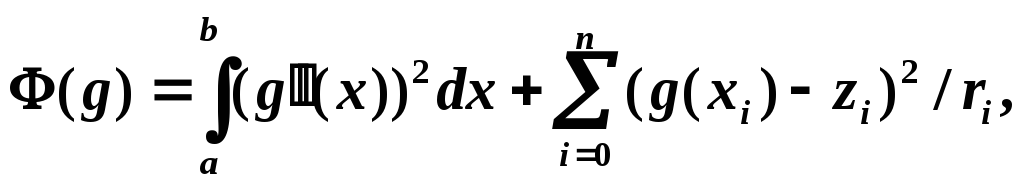где 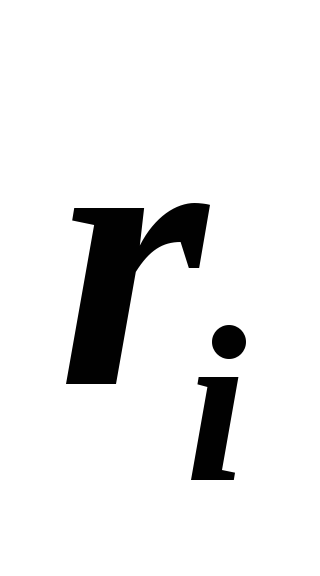- заданные положительные числа, называемые весовыми коэффициентами;

4. краевым условием

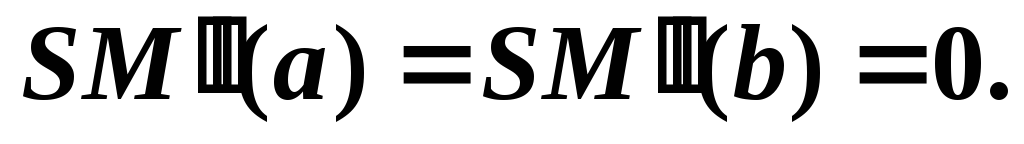
Пример. Функция

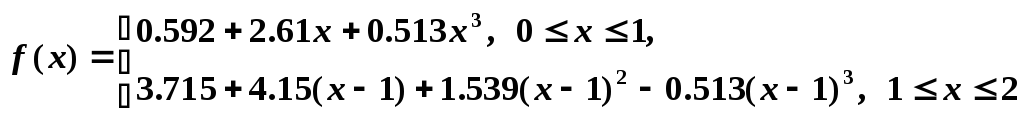
является естественным сглаживающим кубическим сплайном, определенным на отрезке и построенным по следующей таблице:

x	0	1	2
z	0.9	3.1	9.2

при

Теорема существования и единственности. Пусть заданы положительные числа и таблица причем все узлы сетки различны при . Тогда существует единственный естественный сглаживающий кубический сплайн на отрезке

Другими словами если заданы весовые коэффициенты и таблица экспериментальных данных в которой все узлы сетки различны, то существует единственный естественный сглаживающий кубический сплайн, соответствующий этой таблице и весовым коэффициентам.

Производная сглаживающего кубического сплайна – это непрерывно дифференцируемая, кусочно–параболическая функция, то есть параболический сплайн:

Замечание. Весовые коэффициенты задаваемые пользователем, позволяют в известной степени управлять свойствами сглаживающих сплайнов. Если все то и сглаживающий сплайн становится интерполяционным. Таким образом, интерполяционный кубический сплайн можно рассматривать как частный случай сглаживающего кубического сплайна (при ). Отметим, что чем меньше погрешность , тем меньше должны быть весовые коэффициенты Если же необходимо, чтобы сглаживающий кубический сплайн прошел через точку то соответствующий весовой множитель следует положить равным нулю. В практических вычислениях выбор величин является важным вопросом, для решения которого используются различные подходы /9/.