Гипербола

Определение. Гиперболой называется плоская кривая, обладающая сле-дующим свойством: разность расстояний любой ее точки от двух дан-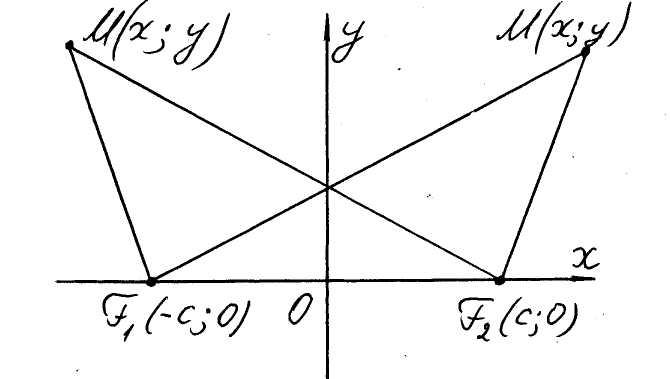ных точек (так называемых фокусов) является постоянной величиной. Как и в случае эллипса, обозначим фокусное расстояние , и расположим фокусы таким же точно образом, .

Полагая на основании определения гиперболы Рис. 4 (рис. 4, где теперь ), получаем уравнение - каноническое уравнение ги-перболы

, ( 9 )

где число определяется по формуле

. ( 10 )

Гипербола симметрична относительно ко-ординатных осей и начала координат. Она пере-секает ось в двух точках , , то есть обладает только двумя вершинами. С осью Рис. 5 Oy гипербола не пересекается и, следовательно, состоит из двух ветвей (рис. 5).

Число a называется вещественной полуосью, а b – мнимой полуосью гиперболы.

Прямые образуют так называемый основной прямоугольник гиперболы, диагонали которого, то есть прямые

, ( 11 ) называются асимптотами гиперболы. Смысл этого термина состоит в следую-щем. Если точка гиперболы уходит в бесконечность, она неограниченно приб-лижается к одной из асимптот.

■Пусть, например, точка находится в первой четверти и уходит в бесконечность. Выразив y через x с помощью уравнения (9),

,

мы убеждаемся в том, что при разность

стремится к нулю. А это значит, что точка неограниченно приближае-тся к асимптоте

■

Определение. Эксцентриситет гиперболы определяется аналогичной формулой, что и для эллипса, а именно:

( 12 )

причем, в отличие от эллипса, .

Для построения гиперболы следует сначала построить ее основной пря-моугольник и асимптоты, а затем уже заняться непосредственно самой кривой.

Замечание. Кривая, заданная уравнением

, ( 13 )

также является гиперболой (см. пунктирную линию на рис. 5). Она называется сопряженной гиперболой для гиперболы, заданной уравнением (9). Основной прямоугольник и асимптоты обеих гипербол совпадают, но числа a и b меняют-ся ролями: для сопряженной гиперболы b является вещественной, а a – мнимой полуосями. Эксцентриситет сопряженной гиперболы дается формулой

. ( 14 )

Пример. Найти расстояние от фокуса ги- Рис. 6 перболы (9) до ее асимптот (11).

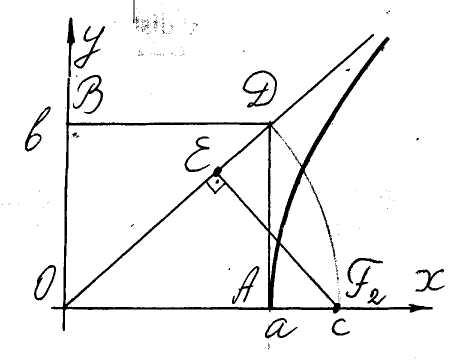
Найдем, например, расстояние от асимптоты (рис. 6).

Прямоугольные треугольники равны по гипотенузе

и общему острому углу . Следовательно,

Пример. Составить каноническое уравнение эл-липса, вершины которого находятся в фокусах гипер-болы

,

Рис. 7 а фокусы – в ее вершинах (рис. 7).

Представим канонические уравнения гиперболы и эллипса в следующем виде:

.

Из Рис. 7 и формул (5), (10) видим, что

,

откуда получаем искомое уравнение эллипса

.