3.2 Перевод из любой сс в десятичную

Перевод чисел из любой системы счислению в десятичную в целом гораздо проще, чем перевод из десятичной в любую. Перевод этот основан на полиномиальной записи числа. Вспомним представление десятичного числа:

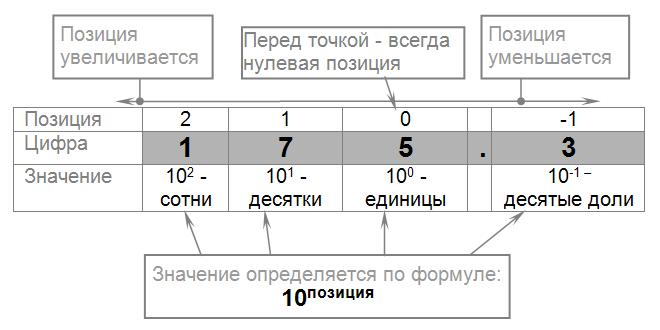
Если взять каждую цифру и умножить её на множитель, соответствующий позиции, то получится полиномиальная запись числа:

1*10²+7*10¹+5*10⁰+3*10^-1=175.3

Такаяа полиномиальная запись числа может использоваться для перевода из любой системы счисления в десятичную: т.е. необходимо исходное число представить в виде полинома по степеням основания системы счисления, а затем вычислить полученное выражение в десятичной системе.

Пример: перевод числа из 18-ричной системы счисления в десятичную:

4E7F.3F1₁₆= 4*16³ + 14*16² + 7*16¹ + 15*16⁰ + 3*16^-1 + 15*16^-2 + 1*16^-3=

16384 + 3584 + 112 + 15 + 0.1875 + 0.05859375 + 0.000244140625 = 20095.246337890625₁₀.

Обратите внимание, что перевод осуществляется в десятичную систему счисления за счёт того, что все операции (возведение в степень, умножение, сложение) выполняются в десятичной системе счисления. Если бы мы с такой же лёгкостью выполняли эти операции в любой другой системе счисления, то этот способ можно было бы использовать для перевода чисел из любой системы счисления в любую другую. На практике же при переводе из любой системы счисления в систему, отличную от десятичной, используют промежуточный перевод: x_n  x₁₀  x_k. Исключение составляют системы со степенями двойки в качестве основания (двоичная, 8-ричная, 6-ричая), где перевод осуществляется путем группировки разрядов.

3.3 Точность чисел в различных системах счисления

Источник ошибок при переводе между разными системами счисления

Важная особенность чисел состоит ещё в том, что целые числа можно представить точно в любой системе счисления. Поэтому дальнейшие рассуждения касаются только дробной части чисел.

Не всякое число может быть точно представлено в выбранной системе счисления.

Например, в десятичной системе счисления невозможно точно записать значение дроби 1/3. В десятичной системе счисления эту дробь обычно записывают так: 0.333333(3). При этом тройка в скобках означает, что она дальше повторяется бесконечное количество раз. Но для практических целей обычно можно записать число просто с определённой точностью. Например, можно записать так: 0.333333. Но при этом нужно понимать, что 1/3 не равно 0.333333. Собственно, когда мы берём и вычёркиваем некоторые наиболее младшие разряды – мы вносим ошибку.

При этом следует отметить, что не во всякой системе счисления число 1/3 невозможно представить точно. Например, в троичной системе счисления 1/3 равно 0.1₃ в точности.

Примеров чисел, которые в одной системе можно представить точно, а в другой нельзя – очень много. Например, 0.6₁₀ – в десятичной системе это точное число. А вот если мы захотим перевести его в двоичную систему счисления, то получим 0.10011001100110011001100110011001(1001)₂. То есть, невозможно точно записать число 0.6₁₀ в двоичной системе счисления без использования бесконечной дроби.

На практике мы обычно округляем до какого-то определённого количества знаков после запятой – именно в этот момент мы вносим ошибку.

Точность и чёткость

Первое, что нужно понять, когда мы имеем дело с разными числами, это отличия между точностью и чёткостью.

Когда речь идёт о числах, то речь всегда идёт о каком-нибудь количестве.

При этом, с одной стороны, как мы говорили выше, не всегда возможно записать это количество абсолютно точно – так или иначе возникает погрешность из-за того, что не все числа возможно записать в выбранной системе счисления. Но у погрешности могут быть и другие причины. Простейший пример: Вы можете просто не знать точного значения либо используемая Вами формула по своему определению не даёт точного результата. Во втором случае сколько цифр не дописывай, точность не повысится. В отличие от первого случая – если точное значение известно, то достаточно всего лишь дописать ещё один младший разряд, и получится более точное значение.

Точность указывает на то, насколько близко Ваше число к реальному значению. Чёткость же относится только к представлению числа и в нашем случае чёткость равносильна количеству цифр в числе.

Значение может быть чётким, не будучи точным, и наоборот. Например, простая цифра 3 является точным представлением числа «Пи» с точностью до одной цифры, но чётким такое представление не является. С другой стороны, число 3.87882 обладает большей чёткостью, но точность у этого числа меньше.

Точность очень часто подменяют чёткостью. Например, могут написать так: «для выполнения этого проекта потребуется 132.2456 часа». Это очень чёткое значение, но, скорее всего, точность оценки времени выполнения проекта не соответствует заявленной чёткости – в реальности может оказаться, что потребуется 132.2456 плюс-минус 10 часов. В таком случае, чтобы не вводить в заблуждение излишней чёткостью, имеет смысл округлить до десятков часов и вместо очень чёткого числа написать менее чёткое, но зато не создающее ошибочное впечатление высокой точности числа: «для выполнения проекта потребуется 130 часов».

Ещё один известный пример подмены точности чёткостью – это расписание движения поездов. Эти расписания обычно обладают чёткостью до одной минуты, но при этом расписания часто оказываются не очень точными.

С другой стороны, известны и немногочисленные обратные примеры – когда точностью жертвовали ради того, чтобы повысить чёткость. Например, согласно первому измерению высоты Эвереста, которое было сделано в 1856 году, высота вершины составляла ровно 29000 футов (8839 м). Но при этом было объявлено, что высота Эвереста составляет 29002 фута (8840 м). Это произвольное добавление было сделано, чтобы из-за круглого числа 29000 не возникло впечатление, что точность измерений невысока.

При переводе чисел между различными системами счисления следует различать точность и чёткость.

Точность перевода – это насколько точно полученное число в новой системе счисления соответствует исходному числу. При этом ошибка в точности может возникнуть из-за того, что мы округлили число в новой системе счисления, использовав какое-то фиксированное (а не бесконечное) количество разрядов.

Чёткость перевода – грубо говоря, это просто количество цифр, которые Вы получили после перевода числа из одной системы счисления в другую. Если точность уже потеряна из-за округления, то дальше, сколько не повышай чёткость, точность не увеличится.

Как определить чёткость числа

По определению, которое мы дали выше, чёткость числа – это количество цифр, которые были использованы при записи этого числа.

Например, число 0.36₁₀ записано с чёткостью в две цифры.

Мы можем легко сравнить два числа и сказать, у какого из них чёткость выше. Например, чёткость у числа 0.36324₁₀ вне всякого сомнения выше, чем чёткость числа 0.3₁₀, потому что в первом случае записано 5 значащих цифр, а во втором – только одна.

Но когда мы имеем дело с числами в различных системах счисления, то для сравнения чёткости не достаточно знать количество цифр.

Например, какое из чисел более чёткое - 0.3₁₀ или 0.1₂? Если Вы уже умеете легко переводить в уме числа из двоичной системы счисления в десятичную с небольшой точностью, то Вы наверняка уже сообразили, что 0.3₁₀ – гораздо более чёткое число, чем 0.1₂, так как в первом случае речь идёт о десятых долях (то есть, три десятых доли), а во втором случае – о половинках (то есть, одна половинка). Если использовать эти числа для записи, к примеру, роста человека, то одна цифра после запятой в десятичной системе счисления означает чёткость записи роста до 10 сантиметров, а одна цифра после запятой в двоичной системе счисления будет означать чёткость записи роста до полуметра.

То есть, чёткость, когда речь идёт о числах в разных системах счисления, – это не просто количество использованных цифр. Теперь, когда мы это знаем, мы можем уточнить понятие чёткости. Простейший способ сделать это – определить чёткость через точность. Итак:

Чёткость числа – это максимальная точность, которую может обеспечить число с таким количеством значащих цифр.

Например, если мы записываем рост человека в десятичной системе счисления с использованием одной цифры после запятой, то максимально возможная точность, которую можно получить при записи таких чисел – до 10 сантиметров. В нашем примере 0.1₁₀ метра – это самая маленькая разница, которая может возникнуть между двумя разными числами.

Самую маленькую разницу очень легко определить для числа в любой системе счисления. Например, если мы записываем рост человека в двоичной системе счисления с использованием одной цифры после запятой, то самая маленькая разница, которая может возникнуть между двумя разными числами составит 0.1₂.

Если записывать три цифры после запятой, то в обоих системах счисления самая маленькая разница (четкость) составит соответственно 0.001₁₀ и 0.001₂ – как видите, изображения чисел абсолютно одинаковые, меняется только система счисления. Если мы захотим представить рост человека в 25-ричной системе счисления с точностью до трёх цифр после запятой, то чёткость составит, как и в предыдущих случаях, 0.001₂₅.

Чтобы понять общую идею, как сравнивать чёткость чисел в разных системах счисления с разным количеством цифр после запятой, начнём со сравнения чёткости чисел в десятичной системе счисления. Например, всем очевидно, что 0.001₁₀ – это гораздо меньше, чем 0.1₁₀. Собственно, именно из этого сравнения мы сразу можем сделать вывод, что число 0.341₁₀ – гораздо более чёткое, чем число 0.3₁₀. Обратите внимание, что вывод этот мы сделали не на основании сравнения количества цифр после запятой (3 цифры или 1 цифра), а на основании сравнения чёткости (0.001₁₀ меньше, чем 0.1₁₀).

Используя это простое правило, мы можем легко сравнить чёткость различных чисел, не зависимо от системы счисления.

Как Вы думаете, какое из чисел чётче - 0.341₁₀ или 0.1011001₂? Чтобы ответить на этот вопрос, запишем чёткость этих двух чисел:

0.341₁₀ – представлено с чёткостью 0.001₁₀;

0.1011001₂ – представлено с чёткостью 0.0000001₂.

Если привести оба числа (0.001₁₀ и 0.0000001₂) к одной системе счисления, мы сможем их сравнить. В данном случае удобнее всего всё привести к десятичной системе счисления, и тогда мы получим, что в двоичной системе счисления число представлено с чёткостью 0.0000001₂=0.0078125₁₀. 0.0078125₁₀ – это больше, чем 0.001₁₀, из этого мы можем сделать вывод, что число в десятичной системе счисления чётче, несмотря даже на то, что в нём использовано меньше цифр (только три), чем в двоичной системе счисления (целых семь цифр после запятой).

Чёткость числа в любой системе счисления можно записать при помощи формулы:

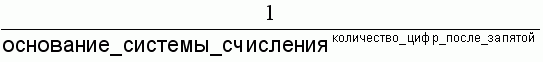
Например, чёткость числа 0.341₁₀ – 1/10³ = 0.001₁₀, а чёткость числа 0.1011001₂ – 1/2₇ = 0.0078125₁₀.

Используя нашу формулу, можно легко сравнить чёткость этих двух чисел:

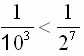
Как определить, сколько цифр должно быть в числе, чтобы это число обеспечивало заданную чёткость?

С самого начала мы узнали, что многие числа невозможно перевести из одной системы счисления в другую точно. При рассмотрении алгоритма перевода числа из десятичной системы в любую другую, мы видели, что для перевода дробной части нужно выполнять операцию умножения столько раз, сколько цифр после запятой в новой системе счисления мы хотим получить. Сколько же раз нужно выполнить эту операцию умножения?

Обычно всё зависит от конкретной решаемой задачи. Например, в компьютерах, при представлении чисел с плавающей точкой, используется мантисса с известным числом разрядов. В таком случае вопрос о том, «сколько разрядов нужно?» не возникает: размерность мантиссы - это и есть количество требуемых разрядов.

Если же количество требуемых разрядов не предопределено заранее, и Вам нужно определить, сколько разрядов нужно, то обычно пользуются следующим простым правилом: чёткость числа не должна пострадать. То есть, чёткость числа в системе счисления, в которую Вы переводите, не должна быть хуже чёткости исходного числа. Добиться этого легко, сравнивая чёткости двух чисел.

Например, мы хотим перевести число 0.341₁₀ в двоичную систему счисления. Сколько нужно двоичных разрядов, чтобы обеспечить чёткость не хуже, чем чёткость исходного числа? Мы можем взять и сравнить чёткость числа в десятичной и в двоичной системах счисления. При этом, поскольку мы не знаем, сколько цифр после запятой будет в двоичной системе счисления, вместо конкретной цифры подставим переменную:

Сравнивая эти две чёткости, мы фактически получим неравенство. Решив это неравенство, мы сможем выбрать такое минимальное n, при котором не пострадает чёткость числа. Самое сложное - это выбрать, какой поставить знак - меньше или больше?

Запомнить очень просто: знак сравнения как бы указывает направление, где лучше чёткость. Поставив правильный знак сравнения:

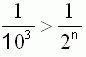
И решив полученное неравенство, получим, что для того, чтобы чёткость числа 0.341₁₀ не пострадала при переводе в двоичную систему счисления, требуется 10 разрядов (10 - это самое маленькое n, при котором будет выполняться это неравенство).

Почему не получится повысить точность, повышая чёткость?

При переводе чисел из одной системы в другую, часто выполняют проверку, выполняя обратный перевод. Например, по следующей схеме:

x₁₀  x₂  x₁₀.

При переводе из десятичной системы счисления точность теряется почти всегда. Точность может также теряться и при переводе обратно в десятичную систему счисления. Это означает, что число, которое Вы получите после такого перевода, не будет равно исходному числу точно. Исходное и полученное числа будут равны между собой только с какой-то точностью. При этом важная особенность состоит в том, что для того, чтобы повышать точность этого равенства, нужно повышать чёткость обоих переводов (и прямого, и обратного), а не только какого-то одного.

Если в приведённом выше примере Вы уже потеряли точность при переводе в двоичную систему счисления, то дальше, сколько не повышай чёткость при переводе из двоичной в десятичную – точность от этого не улучшится.

Например, мы хотим перевести число 0.23₁₀ в двоичную систему счисления, а потом проверить правильность перевода, выполнив обратный перевод.

Воспользовавшись приведённым выше алгоритмом, мы можем определить чёткость числа в двоичной системе счисления такой, чтобы она была не хуже исходного числа. Чтобы достаточно чётко представить число 0.23₁₀, в двоичной системе счисления потребуется 7 разрядов. Таким образом, 0.23₁₀ ≈ 0.0011101₂.

Это двоичное число можно перевести в десятичную систему счисления точно. При обратном переводе получим, что 0.0011101₂ = 0.2265625₁₀. В данном случае равенство точное, так как полученное число в десятичной системе счисления в точности соответствует двоичному числу.

Но оно не равно точно исходному числу 0.23₁₀, так как двоичное 0.0011101₂ является округлённым.

По большому счёту, для целей проверки, нам не требовалось переводить обратно в десятичную систему счисления с точностью до 7 знаков после запятой – достаточно было перевести с точностью до трёх, или даже только до двух знаков после запятой – так как именно такую точность мы заложили, когда выбрали 7 разрядов в двоичной системе счисления.

Можно даже сказать, что сама по себе запись 0.23₁₀ ≈ 0.2265625₁₀ выглядит странно. Вполне достаточно оставить только три цифры после запятой 0.23₁₀ ≈ 0.226₁₀.

Домашнее задание

1. Запишите свою дату рождения в виде число-месяц-год. Переведите каждое из чисел в двоичную, 5-ричную, 8-ричную, 16-ричную системы. Выполните обратный перевод.

2. Запишите число следующего вида:

((месяц-1)*30+день)/365.

Определите четкость исходного числа и необходимое количество разрядов для перевода в двоичную, 5-ричную, 8-ричную, 16-ричную системы. Выполните прямой и обратный перевод.

Домашнее задание

1. Запишите свою дату рождения в виде число-месяц-год. Переведите каждое из чисел в двоичную, 5-ричную, 8-ричную, 16-ричную системы. Выполните обратный перевод.

2. Запишите число следующего вида:

((месяц-1)*30+день)/365.

Определите четкость исходного числа и необходимое количество разрядов для перевода в двоичную, 5-ричную, 8-ричную, 16-ричную системы. Выполните прямой и обратный перевод.