Геометрический смысл производной.

Пусть функция f(z) – аналитическая в области (D). Рассмотрим на плоскости (Z) кривую (l) и на ней точку z₀. Она отобразится на плоскости (W) в кривую (L) и точку W₀ = f(z₀ ). Пусть f′(z₀) ≠ 0. Пусть далее z = z₀ + ∆z, w = w₀ + ∆w.

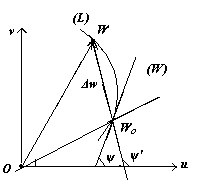
Тогда

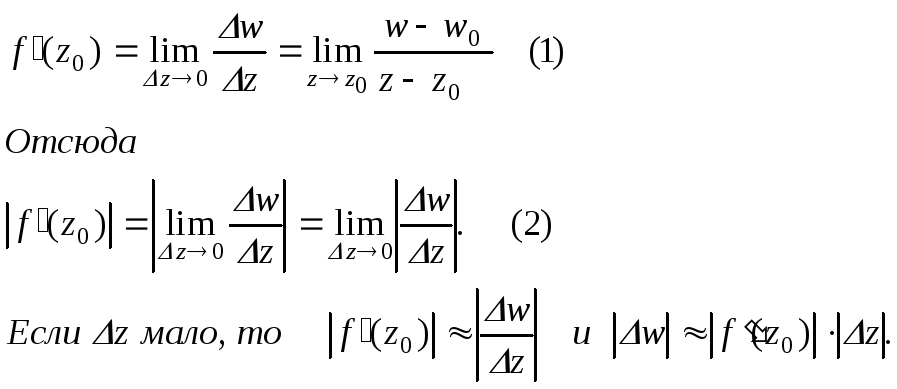
Следовательно, |f′(z₀)| - коэффициент растяжения в точке z₀ при отображении w = f(z).

В силу аналитичности функции f(z) пределы (1) и (2) не зависят от способа приближения точки z к точке z₀, т.е. от выбора кривой (l). Это означает, что предел (2) один и тот же во всех направлениях выходящих из z₀.

arg f′(z₀) =.

Отсюда, ψ = arg f′(z₀) + φ.

Таким образом, arg f′(z₀) – угол, на который надо повернуть касательную к кривой (l) в точке z₀, чтобы получить направление касательной к кривой (L) в точке w₀. В силу аналитичности функции w = f(z) величина arg f(z₀) одна и та же для всех кривых (l), проходящих через точку z = z₀.

Следовательно, при отображении с помощью аналитической функции углы между кривыми в точке z₀ сохраняются.

Отображения, обладающие в данной точке свойством консервативности углов и свойством постоянства растяжения, называются конформными отображениями в этой точке.

Аналитическое отображение является конформным, если f′(z) ≠ 0.

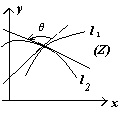
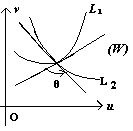
Интегралы от функций комплексного переменного.

Рассмотрим непрерывную функцию комплексного переменного

W = f(z) = u(x,y) + i v(x,y).

y Z_k+1 Пусть (l) - кусочно-гладкая линия, на которой указано

начало и конец (т.е. линия ориентирована, эта линия

∆Z_k Z_k может быть и замкнутой). Разобьем кривую

(l) произвольным образом на участки и найдем

x

z_k = x_k + i y_k, ∆z_k = ∆x_k + i ∆y_k .

Этот предел называется контурным интегралом от функции f(z) вдоль линии (l).

Очевидно,

Контурные интегралы обладают всеми свойствами криволинейных интегралов. Отметим два из них.

A

C

B

Вычисление контурных интегралов.

Пусть x = x(t), y = y(t) – параметрические уравнения кривой (L). Или в комплексной форме z = x(t) + i y(t). t = t_A → A, t = t_B → B.

Отсюда

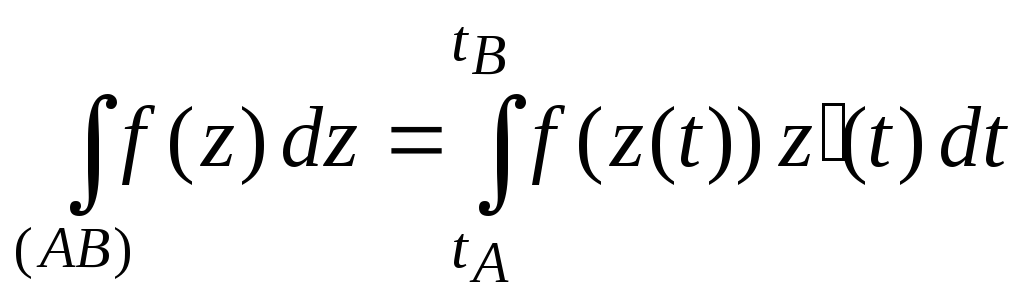
П р и м е р .

y

x = 2t, t₀ = 0, t_A = 1, z = 2t + i t, |z| =

z = 2 + i y = t.

A

O 2 x

Теорема Коши.

Пусть функция f(z) аналитическая в области (D).

Теорема.

Если функция f(z) аналитическая в замкнутой односвязной области (D), то интеграл по замкнутому контуру, ограничивающему эту область, равен нулю.

Эта теорема распространяется и на многосвязную область.

(L) Сделаем разрезы γ₁ и γ₂. Область стала односвязной.

Следовательно,

(Γ) – контуры (L), (L₁), (L₂) и разрезы (γ₁) и (γ₂)_. Разрезы

проходятся дважды в противоположных направлениях, в

силу чего интегралы по этим разрезам взаимно

Llllll ( γ₁) уничтожаются. Следовательно,

Γ

(L)

Или

(γ₂)

П р и м е р .

2. n > 0, но точка z = a лежит вне контура (L).

(L) ● z = a

3. n > 0, и точка z = a лежит в области, ограниченной контуром (L).

Проведем окружность (С) с центром в точке z = a и радиусом R, не пересекающую (L). Уравнение окружности имеет вид:

|z – a| = R, или z – a = R e^iφ, z = a + Re^iφ.

Функция аналитическая в области

(L) между (L) и (С). Следовательно,

z = a

(C)