Пример 2.6

На рис. 2.15 изображено дерево, рядом с вершинами которого  указаны их кортежи. В скобках указаны уровни центральных вершин, их две, т.е. дерево  бицентральное. Если центральные вершины совместить (слить), удалив инцидентное им ребро, то получим центральное дерево, центр v которого будет иметь кортеж:

k(v) = 24 13 941113111311 611111 4321 1.

 

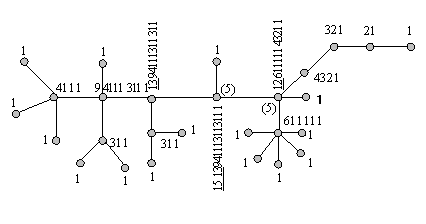Рис. 2.15. Кортежи вершин дерева

 

Теорема 2.10. Для того чтобы два дерева были изоморфны необходимо и достаточно, чтобы они оба были центральными (или бицентральными) и кортежи их центров совпадали.

(Без доказательства).

2.4. Паросочетания и двудольные графы

 

            Наибольшее паросочетание

            Метод чередующихся цепей

            Хроматическое число

            Двудольные графы

            Наибольшее паросочетание в двудольном графе

            Гамильтоновы цепи и циклы в двудольном графе

 

Наибольшее паросочетание

Паросочетанием простого графа G = (V, E) называется такое подмножество R  E его ребер, в котором никакие два ребра не имеют общей инцидентной вершины. Ребра, не имеющие общих инцидентным им вершин, называются независимыми. Поэтому иначе можно сказать, что паросочетание это множество независимых ребер.

Пример 2.7

На рис. 2.16 задан граф G, который содержит паросочетание R₁ = {2} (рис. 2.16,б) и паросочетание  R₂ = {1, 3} (рис. 2.16,с).  

 

Рис. 2.16. Граф  G (а) и его возможные паросочетания: R₁ = {2} (б); R₂ = {1, 3} (в)

 

Одной из важных задач на графе является задача нахождения паросочетания (паросочетаний, если их несколько) с наибольшим  количеством ребер. Число ребер такого паросочетания (наибольшего паросочетания) обозначается через (G). Это число является инвариантом для графа G в том смысле, что для любого графа F, изоморфного G, имеем: (F) = (G). Для графа из примера 2.7   (G) = 2.

Метод чередующихся цепей

Граф G с выделенным в нем паросочетанием  R обозначают  через G_R, ребра R с инцидентными им вершинами называют толстыми, а остальные ребра и вершины графа G_R – тонкими. Иначе, вершины инцидентные ребрам паросочетания, называют насыщенными.

Чередующейся цепью в графе G_R (относительно выделенного паросочетания) называется простая цепь ненулевой длины, ребра которой поочередно то тонкое, то толстое.

Чередующаяся цепь в G_R называется  R-увеличителем, если она соединяет тонкие (ненасыщенные) вершины.

Из этих определений следует, что  концевые ребра R-увеличителя тоже тонкие.

С помощью R-увеличителя легко переделать паросочетание R графа  G  в другое паросочетание _R, содержащее на одно ребро больше, заменив в графе G_R  все тонкие ребра увеличителя на толстые, а все толстые ребра – на тонкие.

Пример 2.8

На рис. 2.17 показано преобразование паросочетания R в паросочетание _R.

 

Рис. 2.17. Преобразование паросочетаний

 

Если граф , в свою очередь, имеет _R-увеличитель, то можно увеличить результат еще на 1 и т.д. Этот процесс можно использовать для решения задачи о наибольшем паросочетании. При этом процесс заканчивается, если выполняются условия следующей теоремы.

Теорема 2.11. Если количество ребер в паросочетании R  меньше, чем (G), то в графе G_R = (V, E) существует R-увеличитель.

Доказательство. Пусть в G = G_R паросочетание R  не является наибольшим, т.е. в G есть другое паросочетание T с большим числом ребер, чем в R. Рассмотрим суграф H графа G с ребрами из множества:  F = (R \ T)  (T \ R). Покажем, что степень каждой вершины этого суграфа не превышает двух. Действительно,

        все вершины суграфа H, не являющиеся инцидентными ребрам из множества F, изолированы;

        если некоторая вершина инцидентна ребру из паросочетания R, но не является инцидентной ребру из T, то ее степень равна единице, так как R – паросочетание;

        если некоторая вершина инцидентна ребру из паросочетания T, но не является инцидентной ребру из R, то ее степень равна единице, так как T – паросочетание;

        если некоторая вершина инцидентна ребру из  множества  (R \ T) и ребру из  (T \ R), то она имеет степень 2, в противном случае должно существовать еще одно ребро, принадлежащее одному из рассмотренных множеств, это противоречит тому, что R и T – паросочетания.

Других вершин нет. Отсюда следует, что каждая компонента суграфа H представляет собой простую цепь или простой цикл с чередованием ребер из R и T. Среди этих компонент обязательно есть простая цепь нечетной длины, начинающаяся и оканчивающаяся ребрами паросочетания T, так как ребер  в T больше, чем в R. Ясно, что это будет искомый R-увеличитель в G_R.

 

Двудольные графы

Двудольным графом называется граф G, множество вершин V которого допускает разбиение: {V₁, V₂}, где V₁ и V₂ содержат попарно несвязные вершины.

Двудольный граф более подробно записывается как G = (V₁ , V₂ , E), где V₁  V₂ = V, V₁  V₂ = , при этом ребра E могут соединять вершины только из V₁ (цвета 1) с вершинами из V₂ (цвета 2).

К понятию двудольного графа приводит ряд задач дискретной математики.