24

§ 5. Распределение молекул по проекциям скорости в состоянии термодинамического равновесия

Функция распределения

На систему, состоящую из большого числа частиц, могут действовать силы, учет которых принципиально невозможен. Такие воздействия носят случайный характер и называются стохастическими. Они могут быть связаны с молекулярным (микроскопическим) движением, оказывающим влияние на поведение макроскопической системы. Широко распространены явления, когда стохастические воздействия оказывают определяющее влияние на поведение системы, т.е. выполняется неравенство . Когда для системы выполняется это условие, связь между состояниями не является взаимно однозначной, а поведение системы подчиняется вероятностным закономерностям, на основе которых по известному набору параметров состояния в некоторый момент времени определяется вероятность состояния.

Для определения характера поведения системы, на которую оказывается стохастическое воздействие, необходимо установить вид функции распределения. Функция распределения характеризует особенности стохастических воздействий в анализируемом процессе.

Макроскопическую систему, т.е. совокупность большого числа микрочастиц, представляющую собой идеальный газ, как раз и характеризует определяющее влияние стохастических сил, а параметры ее определяются функциями распределения.

Каждая микрочастица, входящая в состав макросистемы, обладает некоторой скоростью, энергией, имеет определенные координаты. У различных микрочастиц все эти величины могут быть различными, хотя могут частично совпадать. Пусть общее число частиц макросистемы N. Обозначим через dN()-число частиц, имеющих скорости в интервале от  до +d (d-элементарное приращение). Ясно, что чем больше общее число частиц N и чем больше интервал скоростей d,тем больше будет dN: dN()N, dN()d.

Коэффициент пропорциональности для различных значений  может быть разным, поэтому можно записать

dN()=f()Nd, (1)

Функция f() и есть функция распределения микрочастиц по скоростям (аналогично, по координатам, энергии). Ясно, что

(2)

dN/N показывает, какая часть частиц имеет скорости в интервале от  до +d , т.е. вероятность того, что частицы имеют скорость в этом интервале.

Если dN/N, т.е. вероятность, разделить на d , т.е. на интервал возможных значений параметра, то мы получим плотность вероятности.

Таким образом, функция распределения - суть плотность вероятности обнаружения микрочастицы с заданным значением параметра (скорость, координата, энергия).

Поскольку dN=N, то получим

, (3)

т.е. - это условие нормировки функции распределения, которое означает, что вероятность обнаружить частицу с данным значением скорости во всем диапазоне скоростей от - до +  равна 1.

Для описания макросистемы применяют различные виды функции распределения:

• функция распределения по проекциям скорости;

• функция распределения по абсолютному значению скоростей;

• функция распределения по координатам;

• функция распределения по скоростям и координатам;

• функция распределения по энергиям.

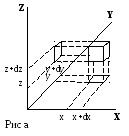
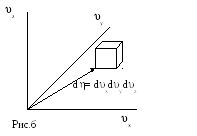
dN(x, y, z)=f( x, y, z) N dxdydz – число частиц, попадающих в элементарный объем dxdydz=dV- (рис. а).

(4) - это плотность вероятности того, что конец радиус- вектора, определяющего положение микрочастицы, лежит в элементарном объеме dV вблизи точки с координатами x, y, z. Аналогичные рассуждения можно провести и для распределения по компонентам скорости. В этом случае говорят о фазовом пространстве скоростей (_x,_y,_z) и элементе фазового пространства d= d_xd_yd_z (рис. б).

В общем случае определяют вероятность обнаружения микрочастицы в единичных интервалах вблизи некоторого значения координат и компонент скорости

dN(_x, _y, _z,x, y ,z)=f(_x, _y, _z ,x, y, z)N d_xd_yd_z dxdydz, (5) f(_x, _y, _z ,x, y, z) -функция распределения по скоростям и координатам; d_xd_yd_z dxdydz – элементарный объем 6-тимерного фазового пространства.

Что же даёт нам знание функции распределения некоторой системы?

Во-первых, функция распределения показывает, в каком интервале могут находиться параметры (скорости, координаты, энергия) микрочастиц системы и какие значения параметров наиболее вероятны.

Во- вторых, функция распределения позволяет определять средние значения физических величин макросистемы, зависящих от координат и скоростей. А именно, средние значения проявляются и определяются на опыте.

Термодинамическое равновесие – наиболее простое состояние молекулярной системы – системы многих частиц. В этом состоянии господствует хаос молекулярного движения, нет преимущественных потоков частиц, энергии, вообще нет никаких макроскопических потоков. Однако же молекулярное движение существует. Как мы уже знаем, его средняя кинетическая энергия в расчете на одну молекулу идеального газа, материальную точку массой m, равна (3/2)kT. Получить закономерность распределения молекул по скоростям – сложная задача даже в условиях термодинамического равновесия. Однако простота состояния хаоса позволила Максвеллу если не вывести, то во всяком случае, как это понятно с позиций современности, догадаться, какой вид должна иметь эта зависимость. Следуя Максвеллу, отметим, что состояние хаоса позволяет нам сделать вывод о полной независимости движения моделирующих молекулы материальных точек по всем трем степеням свободы. Это значит, что функции распределения молекул по компонентам скоростей v_x v_y v_z должны иметь одинаковый вид f(v_x) = f(v_y) = f(v_z). С другой стороны, если события, в которых молекула имеет значения компонентов скоростей v_x v_y v_z независимы, то вероятность одновременно иметь значения компонентов v_x v_y v_z определяется произведением соответствующих вероятностей:

f(v_x v_y v_z) = f(v_x)f(v_y)f(v_z). (6)

Что же можно сказать о виде функции f(v_i)? Из тех же закономерностей хаоса очевидно, что функция распределения по компонентам скоростей является симметричной относительно изменения знака компоненты скорости, f(v_i) = -f(v_i). Это означает, что f(v_i) является четной функцией компонентов скорости, в простейшем случае – четной степени компонентов скорости. Но какой степени? Здесь нам поможет обращение к механике. При анализе механического движения мы встречались с функцией скорости, прежде всего – импульсом, и функцией квадрата скорости – кинетической энергией. Из физических соображений ясно, что, как это полагал Максвелл, искомой четной функцией от скорости является кинетическая энергия:

. (7)

В результате, соотношение (1) может быть представлено в виде:

(8)

Прологарифмируем соотношение (3), чтобы перейти от произведения к сумме функций:

(9)

Так как

(10)

при ,

то при E(v) = const, f(v) = const, в том числе, при изменении соотношения между вкладами в кинетическую энергию при движении по отдельным степеням свободы. При учете этого условия продифференцируем соотношение (4) по вкладам в кинетическую энергию, соответствующим движению по отдельным степеням свободы.

(11)

(12)

(13)

Вследствие симметрии функции f(v) левые части уравнений (11-13) равны.

Тогда следует, что правые части этих уравнений должны быть равны некоторой универсальной величине, не зависящей от скорости или какой либо ее проекции.

(14)

В этом случае, для любой из проекций

, (15)

Интегрирование дает:

(16)

Постоянную A_i можно определить из условия нормировки:

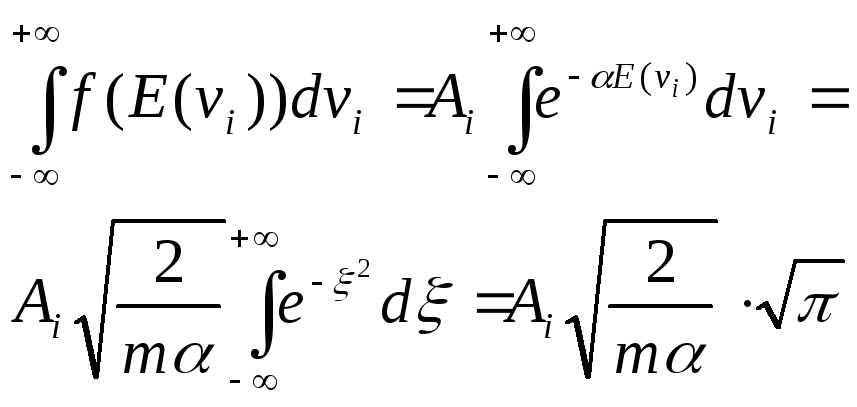(17)

Откуда 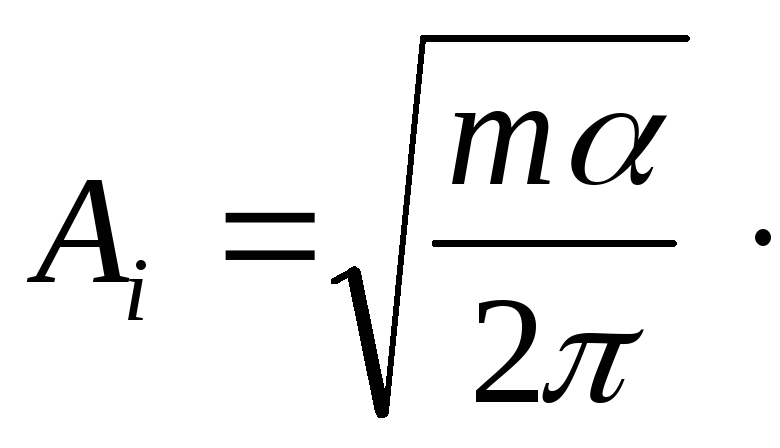(18)

Знание функции распределения молекул по проекциям скорости обеспечивает возможность определения средней величины кинетической энергии, обусловленной движением по данной степени свободы:

. (19)

На основе кинетической теории уже было получено, что средняя энергия, приходящаяся на одну степень свободы, равна (1/2)kT, откуда следует, что  = (1/kT).

Итак, функция распределения молекул по проекциям скоростей на ось ОХ имеет вид:

. (20)

Аналогичный вид имеют функции распределения молекул по проекциям скоростей на оси ОY и OZ:

, (21)

. (22)

Теперь легко определить вероятность того, что молекула одновременно имеет проекции скорости в интервалах , , . Или, согласно эргодической гипотезе, долю молекул, имеющих одновременно проекции скорости в указанных интервалах

, (23)

где функцию можно трактовать как функцию распределения молекул по векторам скоростей. В пространстве скоростей вероятность, задаваемая последним выражением, показывает вероятность того, что конец вектора скорости молекулы попадает в параллелепипед с ребрами вблизи точки с координатами .

Учитывая вид функций распределения молекул по модулям скоростей (20), (21), (22), получаем

. (24)

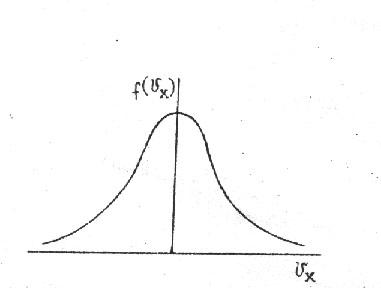
Графики функций (20) – (22) и (24) симметричны относительно начала координат

Рис. График функции распределения молекул по проекциям скорости на ось ОХ

Рис. 1.5.??. График функции распределения молекул по векторам скоростей в ??двумерном случае.