
2. Пряма.
Я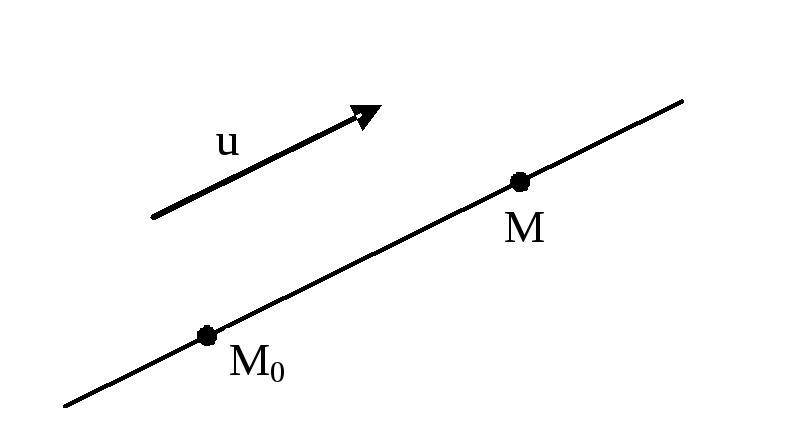 кщо
зафіксувати деякий вектор
кщо
зафіксувати деякий вектор
![]() ,
то він задає напрямок у просторі. Тим
самим визначена множина прямих паралельних
даному напрямку. Для визначення конкретної
прямої
,
то він задає напрямок у просторі. Тим
самим визначена множина прямих паралельних
даному напрямку. Для визначення конкретної
прямої
![]() з цієї множини, досить вказати точку
з цієї множини, досить вказати точку
![]() на ній (див мал. 1). Щоб визначити цю пряму
аналітично, тобто вказати рівняння, яке
пов’язує координати довільної точки
прямої
на ній (див мал. 1). Щоб визначити цю пряму
аналітично, тобто вказати рівняння, яке
пов’язує координати довільної точки
прямої
![]() ,
скористаємось колінеарністю векторів
,
скористаємось колінеарністю векторів
![]() та
та
![]() (вектор
(вектор
![]() називається напрямним
вектором
прямої) :
називається напрямним
вектором
прямої) :
![]() або
або
![]() ,
де
,
де
![]() – довільне число. Таким чином одержане
векторне
рівняння прямої
– довільне число. Таким чином одержане
векторне
рівняння прямої
![]() .
.
Ця
ж рівність для кожної координати вектора
![]() дає параметричні
рівняння прямої
дає параметричні
рівняння прямої
![]() :
:
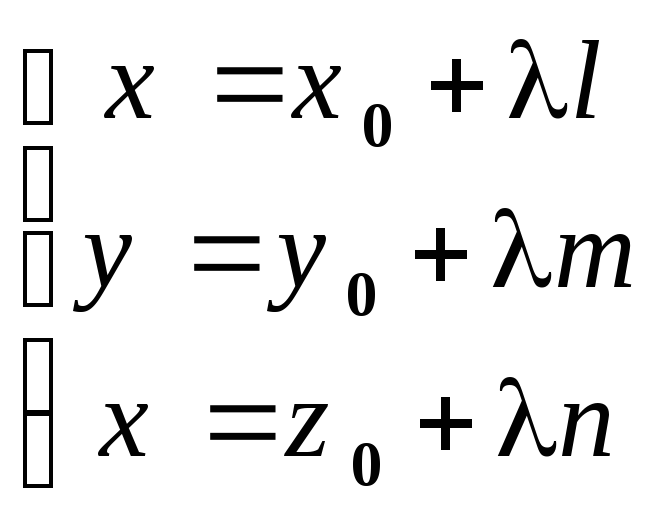 .
(1)
.
(1)
Рис.
1 Тут
![]() є параметром – кожна точка прямої
визначена деяким його
є параметром – кожна точка прямої
визначена деяким його
значенням.
Якщо з рівностей (1) виключити параметр
![]() ,
то одержимо канонічні
рівняння прямої:
,
то одержимо канонічні
рівняння прямої:
![]() (2)
(2)
Розглянемо
деякі частинні випадки. Припустимо, що
одна з координат напрямного вектора
прямої (2) рівна нулю, наприклад,
![]() .
Тоді пряма, очевидно, перпендикулярна
осі абсцис. Якщо ж
.
Тоді пряма, очевидно, перпендикулярна
осі абсцис. Якщо ж
![]() ,
то пряма перпендикулярна до площини
,
то пряма перпендикулярна до площини
![]() , тобто паралельна осі аплікат.
, тобто паралельна осі аплікат.
Пряму
також можна задати, вказавши дві точки
![]() та
та
![]() на ній. Нехай
на ній. Нехай
![]() – довільна точка шуканої прямої. Тоді
вектор
– довільна точка шуканої прямої. Тоді
вектор
![]() буде напрямним і можемо записати
канонічні рівняння
прямої, заданої двома точками:
буде напрямним і можемо записати
канонічні рівняння
прямої, заданої двома точками:
![]() .
.
Пряма у просторі може також бути визначена як лінія перетину двох непаралельних площин:
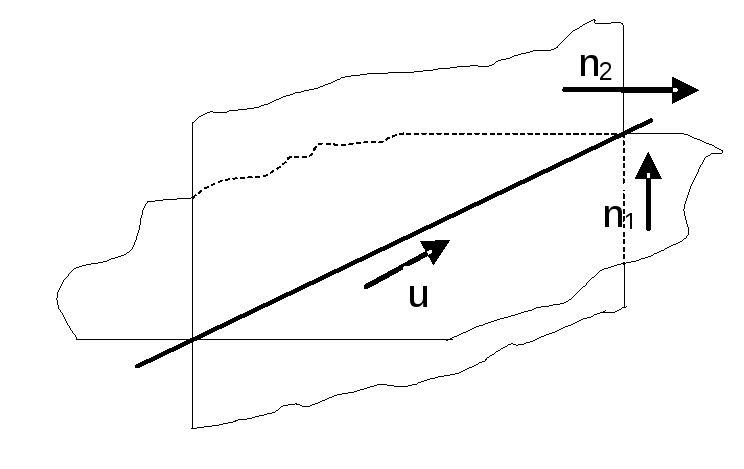
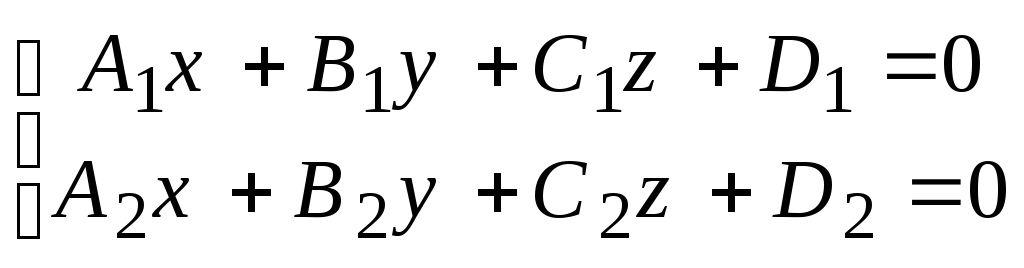 (3)
(3)
Ці
рівняння описують площини, проте дають
мало уявлення про власне пряму. Щоб
записати пряму, задану рівнянням (3), у
канонічному вигляді, необхідно визначити
напрямний вектор прямої та деяку точку
на ній. Напрямний вектор, очевидно, має
бути паралельним кожній з площин, а
отже, перпендикулярним до нормалей
![]() та
та
![]() обох площин, тому Рис.
2
можна вважати, що
обох площин, тому Рис.
2
можна вважати, що
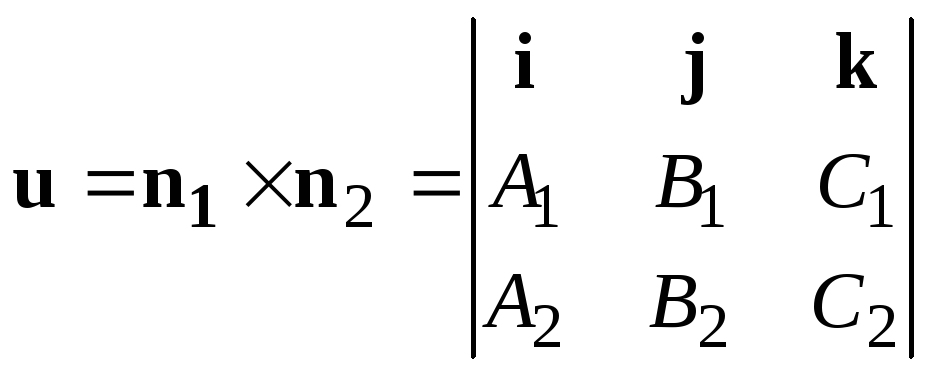 .
Для того, щоб визначити точку на прямій
(3), покладемо одну із змінних, наприклад
.
Для того, щоб визначити точку на прямій
(3), покладемо одну із змінних, наприклад
![]() ,
рівною
,
рівною
![]() і розв’яжемо систему
і розв’яжемо систему
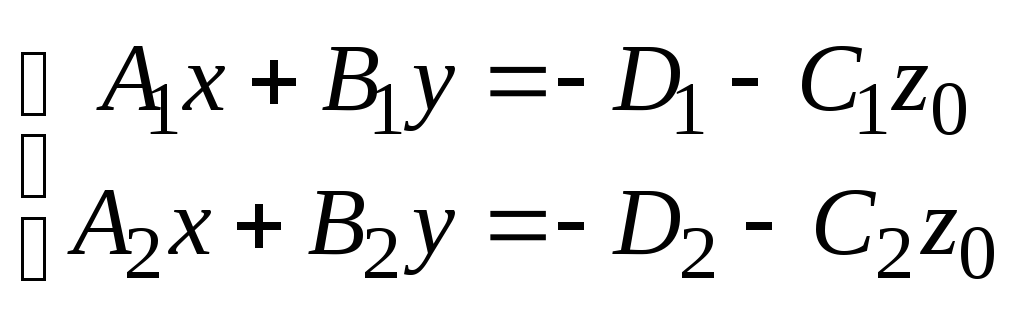 відносно змінних
відносно змінних
![]() та
та
![]() .
.
Приклад
1.
Скласти рівняння прямої, що проходить
через точку
![]() паралельно прямій
паралельно прямій
![]() .
.
Напрямний
вектор
![]() заданої прямої визначаємо із її
параметричних рівнянь:
заданої прямої визначаємо із її
параметричних рівнянь:
![]() .
Шукана пряма паралельна заданій, отже,
вектор
.
Шукана пряма паралельна заданій, отже,
вектор
![]() буде напрямним і для неї. За формулами
(2) визначаємо канонічні рівняння нашої
прямої:
буде напрямним і для неї. За формулами
(2) визначаємо канонічні рівняння нашої
прямої:
![]() .
.
Приклад
2.
Скласти канонічні рівняння прямої
![]() ,
,
![]() .
.
Напрямний
вектор
![]() шуканої прямої визначимо як векторний
добуток нормалей площин:
шуканої прямої визначимо як векторний
добуток нормалей площин:
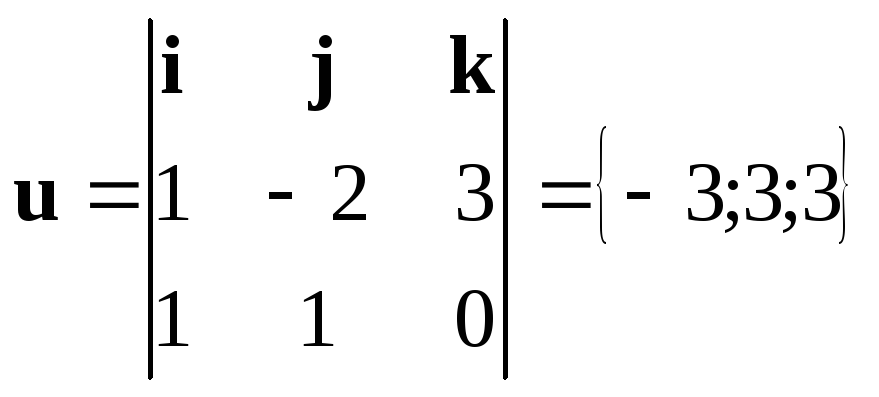 ,
або
,
або
![]() .
Знайдемо ще точку, що належить шуканій
прямій. Покладемо, наприклад,
.
Знайдемо ще точку, що належить шуканій
прямій. Покладемо, наприклад,
![]() та розв’яжемо систему
та розв’яжемо систему
![]() .
Помноживши перше рівняння на
.
Помноживши перше рівняння на
![]() та додавши до другого, знайдемо
та додавши до другого, знайдемо
![]() .
Отже,
.
Отже,
![]() ,
і точка
,
і точка
![]() належить прямій. Запишемо канонічні
рівняння цієї прямої:
належить прямій. Запишемо канонічні
рівняння цієї прямої:
![]() .
.
Зауваження.
Очевидна неоднозначність канонічних
рівнянь (2) – можна було використати
іншу точку на прямій та взяти за напрямний
будь-який вектор, колінеарний до
![]() .
.
Означення
1.
Пучком
площин,
що проходять через вісь
![]() ,
називається вся сукупність площин, що
проходять через пряму
,
називається вся сукупність площин, що
проходять через пряму
![]() .
.
Зауваження. Пучок площин англійською мовою звучить як: pencil of planes або sheaf of planes.
Теорема.
Нехай вісь пучка
![]() задана як лінія перетину двох непаралельних
площин
задана як лінія перетину двох непаралельних
площин
![]() :
:
![]() та
та
![]() :
:
![]() .
Тоді при довільних
.
Тоді при довільних
![]() та
та
![]() ,
таких, що
,
таких, що
![]() ,
пучок задається рівнянням:
,
пучок задається рівнянням:
![]()
Зауваження.
Рівняння пучка у вигляді (4) описує і
обидві площини
![]() та
та
![]() .
Якщо ж покласти у рівнянні (4)
.
Якщо ж покласти у рівнянні (4)
![]() ,
то одержимо рівняння, яке описує всі
площини пучка за винятком площини
,
то одержимо рівняння, яке описує всі
площини пучка за винятком площини
![]() .
.
Приклад
3.
Записати рівняння площини, що проходить
через пряму
![]() та точку
та точку
![]() .
Шукана площина належить пучку з віссю
.
Шукана площина належить пучку з віссю
![]() , або
, або
![]() і описується рівнянням
і описується рівнянням
![]() при деякому значенні
при деякому значенні
![]() .
Щоб визначити
.
Щоб визначити
![]() ,
підставимо в це рівняння координати
заданої точки
,
підставимо в це рівняння координати
заданої точки
![]() :
:
![]() ,
отже
,
отже
![]() .
Тому шуканою є площина
.
Тому шуканою є площина
![]() .
.
