
Число дійсних коренів
Число дійсних коренів з урахуванням кратності або дорівнює степеню рівняння, або на парне число менше. Будь-яке рівняння непарного степеня з дійсними коефіцієнтами має хоча б один дійсний корінь.
У багатьох випадках число дійсних коренів рівняння з дійсними коефіцієнтами можна визначити за правилом Декарта. Перш ніж сформулювати це правило, зробимо деякі зауваження.
1. Ми будемо розглядати кількість змін знаків у даній упорядкованій скінченній послідовності дійсних чисел
![]() (64)
(64)
розуміючи під цим кількість пар сусідніх чисел цієї послідовності, які мають протилежні знаки.
Наприклад,
у послідовності
![]() є
3 зміни знаків, а в послідовності
є
3 зміни знаків, а в послідовності
![]() є 0 змін знаків.
є 0 змін знаків.
Якщо
які-небудь з чисел
![]() дорівнюють 0, то при підрахунку числа
змін знаків їх до уваги не беруть.
дорівнюють 0, то при підрахунку числа
змін знаків їх до уваги не беруть.
Зауважимо,
що коли
перше й останнє числа
![]() і
і
![]() даної послідовності мають однакові
знаки, то кількість змін знаків у
послідовності (64)
парна; якщо ж
даної послідовності мають однакові
знаки, то кількість змін знаків у
послідовності (64)
парна; якщо ж
![]() і
і
![]() мають протилежні знаки, то кількість
змін знаків непарна.
мають протилежні знаки, то кількість
змін знаків непарна.
2. Припускатимемо, що розглядуваний многочлен не має кратних коренів, оскільки завжди можна відокремити кратні множники.
Правило Декарта. Число додатних коренів многочлена з дійсними коефіцієнтами
![]() (65)
(65)
дорівнює числу змін знаків у послідовності його коефіцієнтів або на парне число менше.
Зауваження.
1. Правило Декарта можна застосувати і для оцінки числа від’ємних коренів рівняння з дійсними коефіцієнтами.
2.
Коли наперед відомо, що всі корені даного
рівняння
![]() дійсні, то правило Декарта дає точну
відповідь на питання про число дійсних
коренів, а саме: число додатних коренів
дорівнює числу змін знаків у ряді
коефіцієнтів многочлена
дійсні, то правило Декарта дає точну
відповідь на питання про число дійсних
коренів, а саме: число додатних коренів
дорівнює числу змін знаків у ряді
коефіцієнтів многочлена
![]() а число від’ємних коренів - числу змін
знаків у ряді коефіцієнтів многочлена
а число від’ємних коренів - числу змін
знаків у ряді коефіцієнтів многочлена
![]() .
.
У більшості випадків наперед невідомо, чи всі корені рівняння дійсні. В зв’язку з цим правило Декарта, хоч і зручне з точки зору простоти застосування, не дає повної відповіді на питання про число дійсних коренів рівнянь з дійсними коефіцієнтами та їх розподіл між додатною і від’ємною півосями.
Відокремлення коренів методом Штурма
Далі
перейдемо до питання скільки
дійсних коренів рівняння з дійсними
коефіцієнтами лежить у довільному,
наперед заданому інтервалі
![]() дійсної осі.
дійсної осі.
Повну відповідь на це питання дає метод Штурма.
Нехай
![]() - деякий многочлен з дійсними коефіцієнтами,
- деякий многочлен з дійсними коефіцієнтами,
![]() Припустимо, що
Припустимо, що
![]() не має кратних коренів.
не має кратних коренів.
Знайдемо
похідну
![]() і побудуємо для
і побудуємо для
![]() та
та
![]() алгоритм, подібний до алгоритму Евкліда;
відмінність полягатиме в тому, що всі
остачі
алгоритм, подібний до алгоритму Евкліда;
відмінність полягатиме в тому, що всі
остачі
![]() ми братимемо з протилежними знаками,
тобто
ми братимемо з протилежними знаками,
тобто![]() Позначимо
Позначимо
![]()
![]() Таким
чином, одержимо:
Таким
чином, одержимо:
 (66)
(66)
де
![]() так як
так як
![]() і
і
![]() взаємно прості (за припущенням,
взаємно прості (за припущенням,
![]() не має кратних коренів) і тому
не має кратних коренів) і тому
![]()
Послідовність многочленів
![]() (67)
(67)
називається рядом функцій Штурма, або просто рядом Штурма.
У методі Штурма нас цікавитимуть не самі функції ряду Штурма або їх значення, а лише знаки числових значень цих функцій. У зв’язку з цим функції ряду (67) можна знаходити з точністю до сталого додатного множника, тобто, виконуючи ділення з остачею, домножати на сталі множники; ці множники обов’язково повинні бути додатні, щоб не змінювались знаки значень многочленів.
Введемо
поняття числа
змін знаків у ряді Штурма.
Візьмемо в ряді функцій (67)
![]() де
де
![]() - якесь дійсне число. Тоді скінченна
послідовність функцій (67) перетворюється
в послідовність чисел
- якесь дійсне число. Тоді скінченна
послідовність функцій (67) перетворюється
в послідовність чисел
![]()
![]() ,
,![]()
Число
змін знаків у цій послідовності
позначатимемо через
![]() і називатимемо його числом змін знаків
у ряді Штурма в точці
і називатимемо його числом змін знаків
у ряді Штурма в точці
![]() .
.
Основні властивості ряду функцій Штурма
Лема 1. Ніякі дві сусідні функції ряду Штурма (67) не мають спільних коренів.
Лема
2.
Якщо
![]() є коренем однієї з проміжних функцій
ряду Штурма, то значення сусідніх з нею
функцій ряду Штурма мають у цій точці
протилежні знаки.
є коренем однієї з проміжних функцій
ряду Штурма, то значення сусідніх з нею
функцій ряду Штурма мають у цій точці
протилежні знаки.
Л![]() ема
3.
Якщо
ема
3.
Якщо
![]() ,
зростаючи, проходить через корінь
якої-небудь проміжної функції ряду
Штурма, але не проходить через корінь
,
зростаючи, проходить через корінь
якої-небудь проміжної функції ряду
Штурма, але не проходить через корінь
![]() ,
то число змін знаків у ряді Штурма при
цьому не змінюється.
,
то число змін знаків у ряді Штурма при
цьому не змінюється.
Лема
4.
Якщо
![]() зростаючи, проходить через корінь
многочлена
зростаючи, проходить через корінь
многочлена
![]() ,
то число змін знаків у ряді Штурма
зменшується на одиницю.
,
то число змін знаків у ряді Штурма
зменшується на одиницю.
[Доведення самостійно. Див. Завало С. Т., Костарчук В. М., Хацет Б. І. Алгебра і теорія чисел, ч.2. – К.: Вища школа, 1976. – 384 с. – стор.332-333.]
![]() Теорема
34 (Штурма).
Я
Теорема
34 (Штурма).
Я![]() кщо
кщо
![]() i
i
![]()
![]() довільні дійсні числа, які не є коренями
многочленна
довільні дійсні числа, які не є коренями
многочленна
![]() ,
то число
,
то число
![]() дійсних коренів многочленна
дійсних коренів многочленна
![]() в інтервалі
в інтервалі
![]() дорівнює
дорівнює
![]() ,
де
,
де
![]() і
і
![]() є число змін знаків у ряді Штурма
відповідно в точках
є число змін знаків у ряді Штурма
відповідно в точках
![]() i
i
![]() .
.
Зауваження
1.
Теорема Штурма справедлива і для випадку,
коли кінці інтервалу можуть бути коренями
многочлена. Тільки тоді
![]() є число коренів не на інтервалі
є число коренів не на інтервалі
![]() ,
а на півінтервалі
,
а на півінтервалі
![]() (або на відрізку
(або на відрізку
![]() .
.
Зауваження
2.
Якщо якась з проміжних функцій ряду
Штурма
![]() не має дійсних коренів, то можна наступних
функцій Штурма не знаходити і користуватися
в теоремі Штурма «укороченим» рядом
не має дійсних коренів, то можна наступних
функцій Штурма не знаходити і користуватися
в теоремі Штурма «укороченим» рядом
![]()
Дійсно, число змін знаків у «залишковому» ряді Штурма
![]() ,
,![]() (68)
(68)
є сталими
при будь-якому
![]() .
Адже
.
Адже
![]() може пройти лише через корінь проміжної
функції ряду (68), що, за лемою 3, не впливає
на число змін знаків у цьому ряді. Отже,
«залишковий ряд» (68) не впливає на різницю
може пройти лише через корінь проміжної
функції ряду (68), що, за лемою 3, не впливає
на число змін знаків у цьому ряді. Отже,
«залишковий ряд» (68) не впливає на різницю
![]() .
.
Зауваження
3.
Якщо
![]() має кратні корені, то остання функція
ряду Штурма
має кратні корені, то остання функція
ряду Штурма
![]() вже не є сталою. Але тоді
вже не є сталою. Але тоді
![]()
![]() і можна розглянути ряд многочленів
і можна розглянути ряд многочленів
 (69)
(69)
який
вже має всі властивості, зазначені в
лемах 1-4.Через те що число змін знаків
у ряді (69) збігається з числом змін знаків
у звичайному ряді Штурма
![]() то теорема Штурма залишається в силі.
Слід лише урахувати, що вона дає в цьому
випадку число дійсних коренів не самого
многочлена
то теорема Штурма залишається в силі.
Слід лише урахувати, що вона дає в цьому
випадку число дійсних коренів не самого
многочлена
![]() ,
а многочлена
,
а многочлена
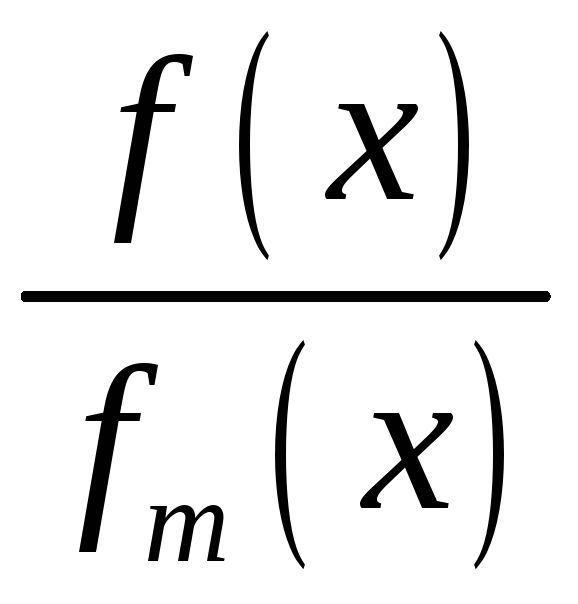 (в якому вже немає кратних коренів),
тобто число різних
коренів многочлена
(в якому вже немає кратних коренів),
тобто число різних
коренів многочлена
![]() в
в
![]() без урахування їх кратності.
без урахування їх кратності.
