Тема 6. Движение твердого тела вокруг неподвижной точки.

П

Рисунок 20

ример 23. Конус с углом при вершине и радиусом основания катится без проскальзывания по неподвижной горизонтальной поверхности. Определить скорость точки , если скорость центра основания постоянна и равна .

Решение. Движение конуса является сферическим. Мгновенная ось вращения конуса совпадает с образующей , так как скорости точек образующей равны нулю (рис. 20).

Используя формулу (5), находим угловую скорость вращения конуса вокруг мгновенной оси вращения: , где . Тогда .

Вектор угловой скорости направлен по мгновенной оси вращения от точки к точке . Скорость точки определим как вращательную скорость вокруг мгновенной оси вращения: , где ; .

Вектор скорости точки направлен аналогично вектору скорости точки , т е. перпендикулярно плоскости в соответствии с направлением угловой скорости вращения.

Ответ. .

Пример 24. Используя условие примера 23, найти ускорение точки А.

Р

Рисунок 21

ешение. Определим угловое ускорение конуса. При качении конуса по горизонтальной поверхности вектор угловой скорости будет вращаться вокруг вертикальной оси . Так как модуль вектора угловой скорости постоянен, то конец вектора описывает окружность постоянного радиуса, равного модулю вектора угловой скорости в горизонтальной плоскости. Угловую скорость вращения вектора вокруг оси определяем, как угловую скорость вращения оси конуса вокруг оси :, где , . Вектор будет направлен противоположно положительному направлению оси . Вектор углового ускорения геометрически равен скорости конца вектора угловой скорости . Ее можно определить, как вращательную скорость точки, радиус вращения которой равен модулю угловой скорости :. Вектор углового ускорения будет находиться в плоскости , приложен в неподвижной точке и направлен в сторону положительного направления оси .

Ускорение точки в сферическом движении равно: . По формулам (7), (8) находим и :, где — отрезок перпендикуляра, опущенного из точки на вектор углового ускорения; . Вектор , перпендикулярный отрезку , находится в плоскости и направлен в соответствии с угловым ускорением, т. е. если смотреть с конца вектора , то вектор должен вращаться против хода часовой стрелки.

Вектор осестремительного ускорения равен , где . . Вектор направлен по к мгновенной оси вращения:

, , .

Ответ. .

Тема 8. Сложное движение твердого тела

П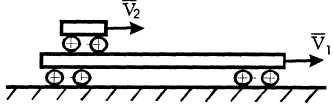ример 25. По платформе движется тележка со скоростью . Платформа движется в ту же сторону со скоростью . Найти скорость тележки (рис. 21)

Р

Рисунок 21

ешение. Скорости тележки и платформы направлены в одну сторону. Применим формулу (1) в скалярном виде и получим абсолютную скорость тележки:

Ответ. .

Пример 26.

Н

Рисунок 22

айти абсолютную угловую скорость подвижного конуса, равномерно катящегося без скольжения по неподвижному конусу, оси которых взаимно перпендикулярны (рис. 22). Известно, что , скорость точки , лежащей на оси конуса, и направлена перпендикулярно плоскости чертежа на читателя.

Решение. Точка при вращении конуса остается неподвижной. Скорость точки при качении без скольжения равна нулю. Мгновенная ось вращения проходит по прямой . Абсолютная угловая скорость вращения будет направлена по мгновенной оси вращения . Угловая скорость вращения конуса вокруг оси равна: , . Вектор будет направлен по от точки к точке . Угловая скорость вращения конуса вокруг оси равна: . Вектор будет направлен по оси вниз от точки к точке . Так как , то абсолютная угловая скорость равна: . Вектор абсолютной угловой скорости направлен по от точки к точке (рис. 22).

Ответ. .

Пример 27. Кривошип вращается с постоянной скоростью и приводит в движение колесо (рис. 23).

Определить положение мгновенной оси вращения и абсолютную угловую скорость, если , , , .

Р

Рисунок 23

ешение. Так как угловые скорости имеют одинаковое направление, то абсолютная угловая скорость равна сумме угловых скоростей кривошипа и колеса :. Для определения положения мгновенной оси вращения составим пропорцию: , , , , .

Следовательно, мгновенная ось вращения будет проходить через точку соприкосновения подвижного и неподвижного колес (рис. 23).

Ответ. , .

П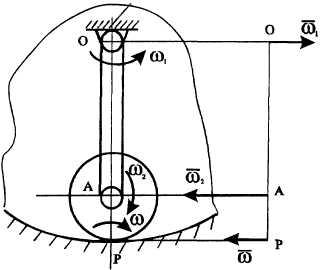ример 28. Кривошип длины вращается с угловой скоростью и приводит во вращение колесо радиуса (рис. 24). Угловая скорость колеса вокруг оси, проходящей через точку равна . Определить абсолютную угловую скорость.

Р

Рисунок 24

ешение. Так как угловые скорости вращений колеса вокруг оси, проходящей через точку и кривошипа вокруг оси, проходящей в точке , направлены в разные стороны, то. Абсолютная угловая скорость направлена в сторону большей угловой скорости и находится за осью, проходящей через точку :, , , , , .

Мгновенная ось вращения находится на расстоянии 20 см, т. е. в точке Р, которая является мгновенным центром скоростей в плоском движении колеса (рис. 24).

Ответ. , .

Пример 29. Колесо катится без скольжения по горизонтальному прямолинейному рельсу (рис. 25). Скорость центра колеса , радиус , относительная угловая скорость . Найти результирующее движение и положение мгновенной оси вращения.

Р

Рисунок 25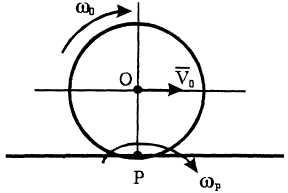

ешение. Ось относительного вращения колеса перпендикулярна плоскости чертежа. Скорость переносного движения перпендикулярна этой оси. Поэтому два движения можем заменить одним вращательным движением вокруг мгновенной оси вращения. Угловая скорость результирующего абсолютного движения равна угловой скорости относительного вращения: . Расстояние между осями будет равно .

О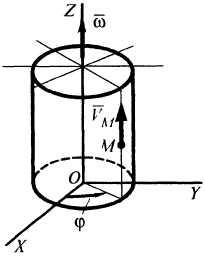твет. Мгновенная ось вращения будет проходить через точку Р.

Пример 30. По образующей цилиндра радиуса движется тело с постоянной скоростью (рис. 26). Определить вид движения тела и шаг винта, если цилиндр вращается с постоянной угловой скоростью .

Решение. Составим уравнение движения точки М в декартовой системе координат:

Рисунок 26

, , , где . Тогда , , — это уравнения винтовой линии в параметрическом виде. Шаг винта равен: .

Ответ. Движение тела винтовое, .