Критерий Рауса — Гурвица

Основная статья: Критерий устойчивости Рауса - Гурвица

Из этой теоремы легко следует критерий устойчивости, так как f(z) — устойчив по Гурвицу тогда и только тогда, когда p − q = n. Таким образом получаем условия на коэффициенты f(z), накладывая дополнительные условия  и .

Наравне с теоремой Стильеса, теорема Рауса — Гурвица дает способы характеризации устойчивых многочленов. Устойчивость — свойство, важное не только в теории функций комплексных переменных. Например, в теории управления рациональный фильтр является стабильным тогда и только тогда, когда его z-преобразованная устойчива. Она является таковой, если многочлен Лорана в знаменателе не имеет корней вне единичной окружности. Решение этой проблемы можно, однако, свести к проблеме устойчивости «обычного» многочлена в изложенной в данной статье формулировке.

Кроме того, соответствие критериев Рауса и Гурвица дает больше информации о структуре простого критерия Рауса, которая видна при изучении более сложного критерия Гурвица.

27\2 – билет 12,вопрос 2

28\1 Критерий устойчивости Найквиста — Михайлова — один из способов судить об устойчивости замкнутой системы управления по её разомкнутой амплитудно-фазовой частотной характеристике. Является одним из частотных критериев устойчивости. С помощью этого критерия оценить устойчивость весьма просто, без необходимости вычисления полюсовпередаточной функции замкнутой системы.

Условие устойчивости

Передаточная функция динамической системы  может быть представлена в виде дроби

.

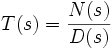Устойчивость  достигается тогда, когда все её полюса находятся в левой полуплоскости на плоскости корней. В правой полуплоскости их быть не должно. Если  получена замыканием отрицательной обратной связью разомкнутой системы с передаточной функцией 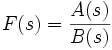, тогда полюса передаточной функции замкнутой системы являются нулями функции  Выражение  называется характеристическим уравнением системы.

Принцип аргумента Коши

Из теории функций комплексного переменного известно, что контур  охватывающий на -плоскости некоторое число неаналитических точек может быть отображён на другую комплексную плоскость (плоскость ) при помощи функции  таким образом, что получившийся контур  будет охватывать центр -плоскости  раз, причём , где  — число нулей, а  — число полюсов функции . Положительным считается направление, совпадающее с направлением контура , а отрицательным — противоположное ему.

[править]Формулировка критерия

Сначала построим контур, охватывающий правую полуплоскость комплексной плоскости. Контур состоит из следующих участков:

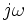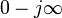• участок, идущий вверх по оси , от  до .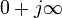

• полуокружность радиусом , начинающаяся в точке 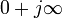 и достигающая конца в точке 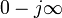 по часовой стрелке.

Далее отображаем этот контур посредством передаточной функции разомкнутой системы , в результате чего получаем плоскость АФЧХ системы. Согласно принципу аргумента число оборотов по часовой стрелке вокруг начала координат должно быть равно количеству нулей функции  минус количество полюсов  в правой полуплоскости. Если рассматривать вместо начала координат точку , получим разницу между числом нулей и полюсов в правой полуплоскости для функции . Заметив, что функция  имеет такие же полюса, что и функция , а полюса разомкнутой системы являются нулями замкнутой системы, сформулируем критерий Найквиста — Михайлова:

Пусть  — замкнутый контур в комплексной плоскости,  — число полюсов , охваченных контуром , а  — число нулей , охваченных  — то есть число полюсов  охваченных . Получившийся контур в -плоскости,  должен для обеспечения устойчивости замкнутой системы охватывать (по часовой стрелке) точку   раз, где .

Следствия критерия Найквиста-Михайлова:

• Если разомкнутая система с передаточной функцией 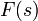 устойчива, замкнутая система является устойчивой, если АФЧХ разомкнутой системы не охватывает точку −1.

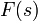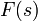• Если разомкнутая система неустойчива, то количество оборотов  вокруг точки −1 должно быть равно числу полюсов  в правой полуплоскости.

• Количество дополнительных охватов (больше, чем 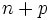) вокруг точки −1 в точности равно количеству неустойчивых полюсов замкнутой системы.

Либо

Критерий устойчивости Михайлова

Пусть ДС описывается уравнением (1) и Перейдем в частотную область  где вещественная часть будет содержать четные степени а мнимая — нечетная степени  Функции и  представляют собой модуль и фазу (аргумент) характеристического полинома. По формулам (21), (22) может быть построен годограф вектора . Определение. Динамическая система устойчива, если годограф Михайлова, начинаясь на положительной ветви вещественной оси, последовательно перемещаясь против часовой стрелки, при изменении  от нуля до бесконечности, проходит n квадрантов и в n-м квадранте уходит в бесконечность. 28\2 – билет 12,вопрос 2

29\1 Критерий устойчивости Найквиста

В 1932 году Найквист предложил принципиально новый критерий устойчивости. В отличие от критерия Гурвица, который устанавливает принадлежность корней к левой полуплоскости для любого полинома или алгебраического уравнения, критерий Найквиста предназначен для исследования устойчивости только замкнутых систем.

Критерий Найквиста — это графоаналитический критерий. Характерной его особенностью является то, что вывод об устойчивости или неустойчивости замкнутой системы делается в зависимости от вида амплитудно-фазовой (а. ф. х.) или логарифмических частотных характеристик (л. ч. х.) разомкнутой системы.

Помимо исследования устойчивости по виду указанных характеристик можно оценить и некоторые качественные показатели замкнутой системы, например, запас устойчивости. Более того, появляется возможность указать, как и за счет каких средств неустойчивая замкнутая система может быть сделана устойчивой и как можно повысить качество устойчивой замкнутой системы.

В главе 5 было введено понятие передаточной функции разомкнутой системы. Эта функция может быть представлена в виде

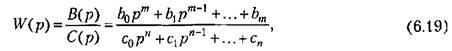
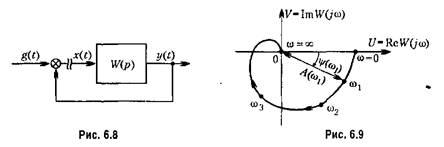
получается частотная передаточная функция разомкнутой системы

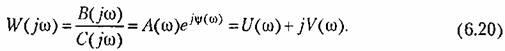
 Модуль частотной передаточной функции представляет собой отношение амплитуд выходной и входной величин:

зависит от

. От частоты зависит и сдвиг фаз, или фаза:

и откладывать на комплексной плоскости точки, соответствующие получающимся комплексным числам, то геометрическое место этих точек образует амплитудно-фазовую характеристику разомкнутой системы (рис. 6.9).

и т.д. Вдоль кривой

иногда рисуют стрелки, которые показывают направление возрастания частоты со (рис. 6.9).

попадает в начало координат.

части. Однако, если порядок системы п > 2, удобнее использовать

 этой целью передаточную функции (6.19) целесообразно представить в так называемой стандартной форме:

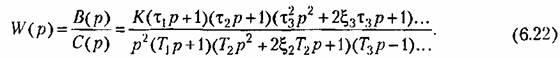
могут принимать любые значения от 0 до 1,

Соответствующая (6.22) частотная передаточная функция разомкнутой системы имеет вид:

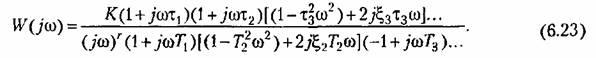
— разности их аргументов. В свою очередь, модуль произведения комплексных чисел равен произведению модулей, а аргумент — сумме аргументов. Модули и аргументы, соответствующие сомножителям передаточной функции (6.22), приведены в табл. 6.1.

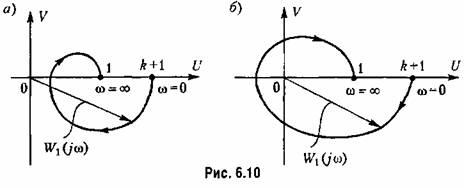
Сформулируем требования к а. ф. х. разомкнутой системы, при выполнении которых замкнутая система будет устойчивой. Ограничим вначале задачу и будем рас

 Ниже будет показано, что при определенных условиях первое ограничение может быть снято. Введем в рассмотрение вспомогательную функцию

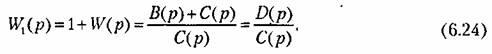
— характеристический полином замкнутой системы.

> и найдем комплекс

не должен охватывать начало

координат (рис. 6.10, а).

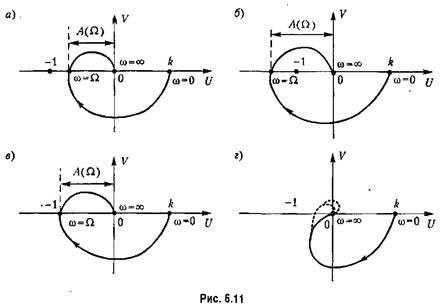
, т. е, должна проходить так, как показано на рис. 6.11, а.

Таким образом, аргумент изменяется на величину

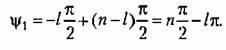
 угол поворота век-

имеется два корпя с положительной вещественной частью.

Эта граница наиболее характерна для устойчивых

в разомкнутом состоянии систем. В этом случае, как следует из выражения (6.16),

, а фаза

  т. е. а. ф, х. разомкнутой системы (рис. 6.11, в) проходит через точку

Тогда замкнутая система будет устойчивой, если

 система

— это частота незатухающих колебаний, возникающих в системе (см. рис. 6.2, г).

как видно из выражения (6.22), зависит от значений постоянных вре-

она становится неустойчивой.

В случае, изображенном на рис. 6.11, г, замкнутая система устойчива при сколь угодно большом значении коэффициента передачи ^разомкнутой системы. Однако практически всегда существуют неучтенные в передаточной функции (6.22) малые

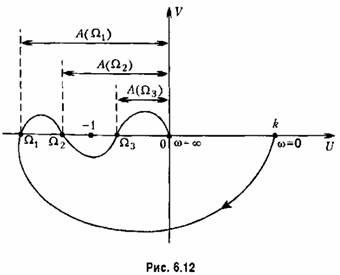
постоянные времени, из-за чего реальная а. ф. х, разомкнутой системы будет такой, как показано пунктиром, а замкнутая система станет критичной к увеличению К.

На рис. 6.12 изображен более сложный случай, когда замкнутая система может стать неустойчивой как при увеличении, так и при уменьшении коэффициента передачи разомкнутой системы. При

то замкнутая система вновь станет устойчивой.

согласно (5.13)

Поэтому система автоматического управления создается не для обеспечения устойчивости объекта, а для придания системе свойств, отличающихся от свойств объекта, например, для повышения точности поддержания управляемой величины (температуры, давления и т, п.) на заданном уровне при наличии возмущений. Однако если алгоритм управления и параметры управляющего устройства выбраны неправильно, то система автоматического управления может стать неустойчивой. Впервые такая ситуация возникла еще в XVIII в. при создании регуляторов скорости вращения валов паровых машин (см. рис. 1.12). И сразу же, как отмечено в § 6.2, появилась необходимость в разработке критериев устойчивости,

Будем полагать, что в нем кроме корней с отрицательными

в знаменателе (6.23) появится со-

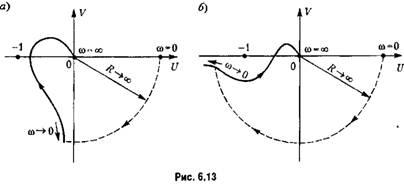
т. е, амплитудно-фазовая характеристика разомкнутой системы будет иметь разрыв непрерывности (рис. 6.13, а). Для получения определенности в ходе

модуль которого

начало которой

находится па вещественной оси, и разрыв непрерывности будет устранен. Кроме того, так как нулевой корень заменен вещественным отрицательным корнем, то разомкнутую систему можно считать устойчивой. Все это означает, что для исследования устойчивости замкнутой системы можно применять приведенную выше формулировку критерия Найквиста.

 (рис. 6.13, б).

. В этом случае (см.

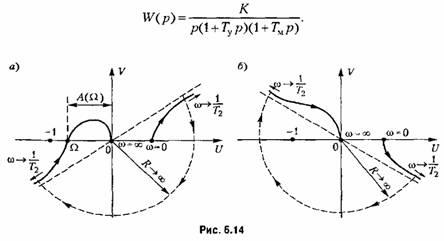
— бесконечно малая положительная величина. Тогда разрыв устранится за счет дополнения а. ф. х. полуокружностью бесконечно большого радиуса по часовой стрелке так, как показано па рис. 6.14.

.В случае рис. 6.14, б замкнутая система неустойчива.

В качестве иллюстрирующего примера рассмотрим следящую систему, структурная схема которой изображена на рис. 6.4. Для этой системы была получена передаточная функция разомкнутой системы

Модуль частотной передаточной функции разомкнутой системы (см. табл. 6.1)

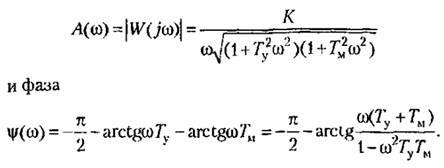
Это означает, что а, ф. х. разомкнутой системы рас-

 а. ф. х. выглядит так, как показано па рис, 6.13, а,

найдем из условия

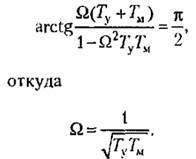
Подставив это значение в выражение для модуля, получим:

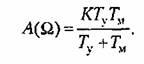
. Таким образом, условие устойчивости замкнутой системы

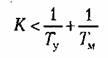
совпадает с найденным ранее условием, вытекающим из критерия Гурвица.

Обратимся теперь к более общему случаю, когда знаменатель передаточной функции разомкнутой системы содержит корпи, лежащие в правой полуплоскости. Это соответствует неустойчивой в разомкнутом состоянии системе.

Появление неустойчивости разомкнутой системы может вызываться двумя причинами. Во-первых, это может быть следствием наличия неустойчивых звеньев, подобных рассмотренным в § 4.8, в том числе и неустойчивости самого управляемого объекта. Во-вторых, это может быть следствием потери устойчивости звеньев, охваченных положительными или отрицательными обратными связями (см., например, рис. 5.4).

  должен составить

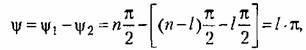
  на угол 1п против часовой стрелки. Приведенная ранее формулировка критерия Найквиста для случая, когда l = 0, вытекает отсюда как частный случай.

Таким образом, при использовании критерия Найквиста необходимо проверить, имеются ли в знаменателе передаточной функции разомкнутой системы корни, лежащие в правой полуплоскости, и сколько имеется таких корней.

Если в системе имеются местные обратные связи, например, такого типа, как это изображено па рис. 5.6, то необходимо убедиться в том, что но цепи местной обратной связи не нарушена устойчивость при разомкнутой главной обратной связи. Проверка устойчивости но цени местной обратной связи может быть сделана посредством использования любых критериев устойчивости, в том числе и посредством критерия Найквиста, который может применяться для разомкнутой местной обратной связи обычным путем построения для этой цели амплитудно-фазовой характеристики.

В случае, если для местной обратной связи будет получено указание на ее неустойчивость, необходимо определить число корней, лежащих в правой полуплоскости.

Следует заметить, что, хотя теоретически вся система в замкнутом состоянии может быть устойчивой при наличии неустойчивости по цепи местной обратной связи, практически такой случай является нежелательным и его надо избегать, стремясь использовать только устойчивые местные обратные связи. Поэтому, как правило, при расчете системы выбирают такие местные обратные связи, которые были бы устойчивыми при разомкнутой главной обратной связи.

В качестве примера рассмотрим систему угловой стабилизации ракеты, структурная схема которой изображена па рис. 6.5. Для этой системы была получена передаточная функция разомкнутой системы

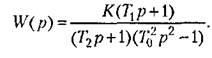
имеется два вещественных отрицательных корня

  свидетельствует о неустойчивости управляемого объекта (ракеты) и разомкнутой системы в целом. Поэтому система автоматического управления создается, в первую очередь, для обеспечения устойчивого полета ракеты.

против часовой стрелки.

Для построения а. ф. х. находим модуль и фазу (см. табл. 6.1)

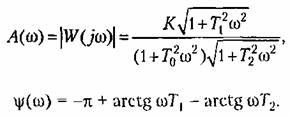
до

Эти условия совпадают с найденными ранее при помощи критерия Гурвица.

— число корней с положительной вещественной частью в характеристическом полиноме разомкнутой системы. При этом переход сверху вниз считается положительным (+1), а снизу вверх — отрицательным (-1).

. Сумма переходов равна нулю и замкнутая система устойчива.

Сделаем теперь замечание, касающееся использования для определения устойчивости замкнутой системы передаточной функции разомкнутой системы.

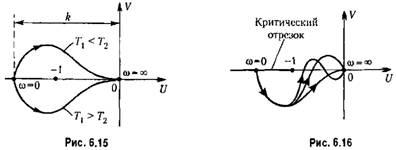
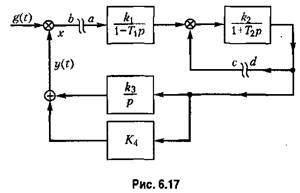
В случае многоконтурной системы управления размыкание ее для получения передаточной функции разомкнутой системы можно делать, вообще говоря, в произвольном месте. Рассмотрим, например, систему, структурная схема которой изображена на рис. 6.17.

Разомкнем систему на входе первого звена. Тогда, рассматривая точку а как вход, а точку b как выход, получаем передаточную функцию разомкнутой системы

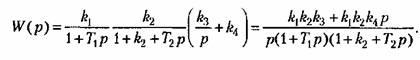
Разомкнем теперь ту же систему не па входе первого звена, а в цепи обратной связи второго звена (точка с соответствует входу, а точка (I — выходу). Передаточная функция разомкнутой системы в этом случае

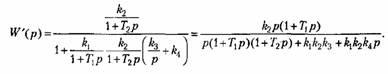
Поэтому для определения устойчивости можно пользоваться передаточной функцией разомкнутой системы, полученной размыканием исходной системы в произвольной точке, в которой выполняется условие детектирования.

связывает между собой изображения управляемой величины и ошибки, и только она связана с передаточной функцией замкнутой системы Ф(р) известным соотношением

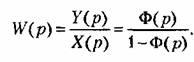
Передаточную функцию при размыкании на входе первого звена в дальнейшем будем считать главной передаточной функцией разомкнутой системы и именно ее иметь в виду при рассмотрении методов определения качества управления и синтеза систем управления.

29\2 – билет 14,вопрос 2

30\1 Установившийся режим

При проектировании систем управления часто требуется оценить ошибку слежения в установившемся режиме . В зависимости от вида воздействия и свойств системы эта ошибка может быть нулевой, постоянной или бесконечно большой величиной.

            Очень важно,  что величина установившейся ошибки  может быть легко найдена с помощью теоремы о предельном значении оригинала: .

            При использовании этой теоремы нужно выразить величину ошибки e (p)  через g(p).  Для этого рассмотрим  структурную схему замкнутой системы управления (рис. 22).

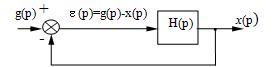
Рис. 22

            Очевидно, e (p) = g(p) - x(p) = g(p) - H(p)e(p).  Отсюда    или  e (p) = He(p)g(p) , где He(p) =  называется передаточной функцией системы управления от входного воздействия g(p) к ошибке слежения e(p). Таким образом, величину установившейся ошибки можно найти с помощью следующего соотношения:

,

где He(p) = 1/(1+H(p));   g(p) -  изображение типового входного воздействия.

            Пример 1.   Рассмотрим систему управления, в составе которой нет интеграторов, например,

                   .

            Найдем  величину  установившейся   ошибки   при   ступенчатом  входном  воздействии g(t) = g0, t ³ 0. В этом случае

.

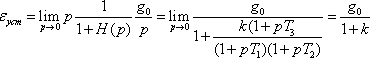            Предположим  теперь, что  входное воздействие изменяется линейно t    или   .

            Тогда   . Соответствующие входные воздействия и переходные процессы можно представить графиками на рис. 23,а и б.

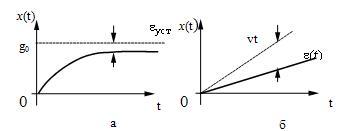
Рис. 23

            Пример 2. Рассмотрим теперь систему, содержащую один интегратор. Типичным примером может быть система сервопривода (рис. 6) с   .

            Для ступенчатого воздействия g(t) = g0    или  g(p) =  получим

.

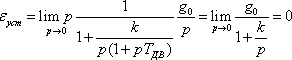При линейном входном воздействии

.

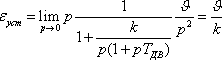Такие процессы можно проиллюстрировать соответствующими кривыми на рис.24, а и б.

Рис. 24

            Пример 3.  Рассмотрим систему с двумя интеграторами. Пусть, например,  . При ступенчатом воздействии .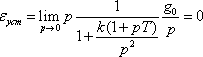

            При линейном     .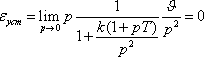

            Наконец, если входное воздействие квадратичное  g(t) = at2/2  (g(p) = a/p3), то     

.

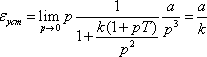            Таким образом, в системе с двумя интеграторами может осуществляться слежение за квадратичным входным воздействием при конечной величине установившейся ошибки. Например, можно следить за координатами объекта, движущегося с постоянным ускорением.

 

30\2 – билет 15,вопрос 2