
matematika_Alene
.pdf
1. Найти общий интеграл дифференциального уравнения 3ху + у2 = ( 2х2 + ху )у′
3ху + у2 = ( 2х2 + ху ) у′ 3ху + у2 =( 2х2 + ху )
3xydx + y2dx = ( 2х2 + ху )dy
3xydx + y2dx = 2х2dy + xydy / :x2
3tdx + t2dx = 2( xdt + tdx ) + t( xdt + tdx )
3tdx + t2dx = 2xdt +2tdx + txdt + t2dx
tdx = x( 2dt + tdt ) / :x и :t
2. Найти решение задачи Коши: y′ + = sin (2x), y ( ) = 1
Решаем методом Лагранжа:
ln ( y ) = - ln( x ) + C

ln ( y ) = - ln( x ) + ln ( C )
Подставим у и у′ в исходное уравнение:
c′(x) = x ∙ sin( 2x )
dc = x ∙ sin( 2x )dx
Подставим с( х ) в

Найдем решение задачи Коши, y ( ) = 1 :
3. Найти решение задачи Коши: y″ + |
|
|
, y (1) = y′ ( ) = 0 |
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдем решение задачи Коши, y′ ( ) = 0, y (1) = 0 y′ ( ) = 0
y (1) = 0
4. Найти общее решение дифференциального уравнения:
y″ + 100y = 20sin( 10x ) – 30cos( 10x ) – 200e10x
y″ + 100y = 0
k2 + 100 = 0 k2 = -100
k =
yoo = c1∙cos( 10x ) + c2∙sin( 10x )
уч = x ( Acos(10x) +Bsin( 10x ) ) + ce10x
Используем формулу: (u∙v)′ = u′v + uv′, u = x, v = Acos(10x) + B∙sin( 10x ) y′ч = 1∙( Acos( 10x ) +Bsin( 10x ) ) + x∙( Acos(10x) +Bsin( 10x ) )′ + 10ce10 x =
=Acos( 10x ) +Bsin( 10x ) + x∙( -10Asin( 10x ) + 10Bcos( 10x )) + 10ce10 x =
=Acos( 10x ) +Bsin( 10x ) + 10x∙( Bcos( 10x ) - Asin( 10x )) + 10ce10 x
y″ = ( Acos( 10x ) +Bsin( 10x ) + 10x∙( Bcos( 10x ) - Asin( 10x )) + 10ce10 x )′=
= -10Asin( 10x ) + 10Bcos( 10x ) +10 ( Bcos( 10x ) - Asin( 10x ) ) + 10x∙( -10Bsin( 10x ) –
10Acos( 10x )) + 100 ce10 x = -20Asin( 10x ) + 20Bcos( 10x ) – 100x(Bsin( 10x ) + Acos( 10x )) + 100 ce10 x
Подставляем в исходное уравнение:
-20Asin( 10x ) + 20Bcos( 10x ) – 100x(Bsin( 10x ) + Acos( 10x )) + 100 ce10 x + 100x∙( Acos(10x) +Bsin( 10x )) + 100ce10x = 20sin( 10x ) – 30cos( 10x ) – 200e10x
-20Asin( 10x ) + 20Bcos( 10x ) + 200ce10x =20sin( 10x ) – 30cos( 10x ) – 200e10x
Отсюда имеем:
y = yч+ уоо = |
c1∙cos( 10x ) + c2∙sin( 10x ) |
Вычислить интегралы:

Решаем методом неопределенных коэффициентов:
2x + 1 = A( x – 1 )( x + 4 ) + Bx( x +4 ) + Cx( x – 1 ) 2x + 1 = A( x2 + 4x – x – 4 ) + Bx2 + 4Bx + Cx2 – Cx 2x + 1 = Ax2 + 4Ax – Ax – 4A + Bx2 + 4Bx + Cx2 – Cx 2x + 1 = x2( A + B + C ) + x(3A + 4B - C) - 4A
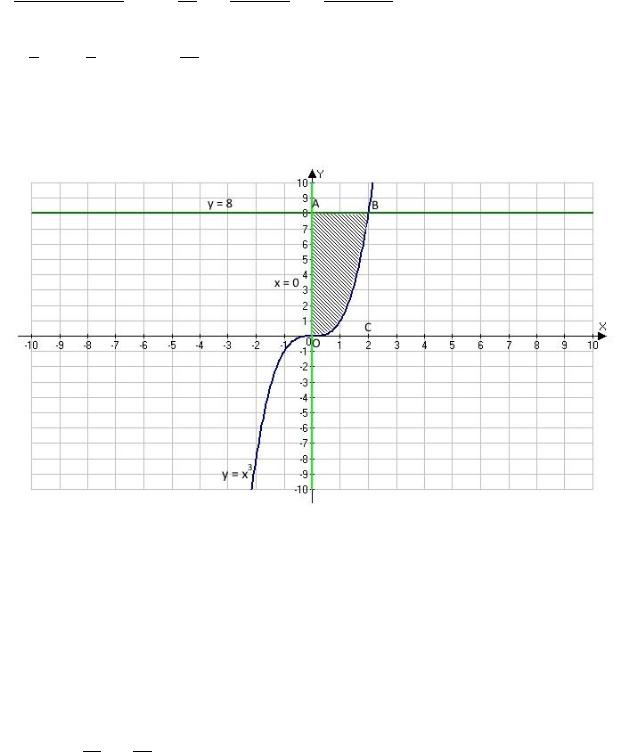
Вычислить площадь фигуры, ограниченной линиями y = x3, y = 8, x = 0
Точки пересечения графиков y = x3 и y = 8: x3 = 8 => x = 2
Пределы интегрирования:
х = 0, х = 2
Найдем площадь фигуры ОВС:
ОАВС - прямоугольник. Найдем площадь фигуры ОАВС:
S = 8 ∙ 2 = 16 кв.ед.
Найдем площадь фигуры ОАВ: SOAB = 16 – 4 = 12 кв.ед.

Воспользуемся признаком Даламбера:
По признаку Даламбера ряд сходится.
Это знакочередующийся ряд, удовлетворяющий условиям теоремы Лейбница. Так как
По теореме Лейбница ряд сходится. Рассмотрим ряд, составленный из модулей:

Следовательно, исходный ряд сходится условно.
Используем признак Даламбера:
Составляем стандартное неравенство:
Исследуем сходимость степенного ряда на концах найденного интервала:

Исследуем полученный числовой ряд на сходимость по признаку Лейбница:
Члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий, значит, убывание монотонно. Ряд сходится. входит в интервал сходимости.
Ряд сходится.
Задание 4. Разложить функцию ln( 1 + x – 12x2 ) в ряд Тейлора по степеням х.
Найдём корни квадратного трёхчлена 1 + x – 12x2 :
-12x2 + x + 1 = 0
D = 1 + 4 (-12) = 49
С учётом того, что логарифм произведения равен сумме соответствующих логарифмов, функция примет вид :
f(x) = ln( 1 + x – 12x2 ) = ln( ) = ln( 4x + 1 )+ ln( 1 - 3x )
Воспользуемся разложением функции ln( 1 + t ) в ряд Маклорена по степеням t:

Тогда f( x ) = ln( 4x + 1 )+ ln( 1 - 3x ) =
Задание 5. Вычислить интеграл с точностью 0,001
Воспользуемся разложением функции y = sin t в ряд Маклорена:
Тогда при t = x2 получим:
Т.к. ряд всюду сходится, интегрируем почленно:
Это знакочередующийся ряд, удовлетворяющий условиям теоремы Лейбница, т.к.
Поэтому остаток ряда не превосходит первого отброшенного члена.
