9. Графоаналитический метод решения

задачи линейного программирования

Транспортная задача является частным случаем задачи линейного программирования на отыскание оптимума – максимума или минимума линейной функции для неотрицательных переменных, связанных системой линейных ограничений в виде неравенств или уравнений.

Если число переменных равно двум, то задача имеет простое графическое (геометрическое) решение.

Пусть требуется найти оптимальное значение функции

(1.5.1)

при ограничениях:

(1.5.2)

(1.5.3)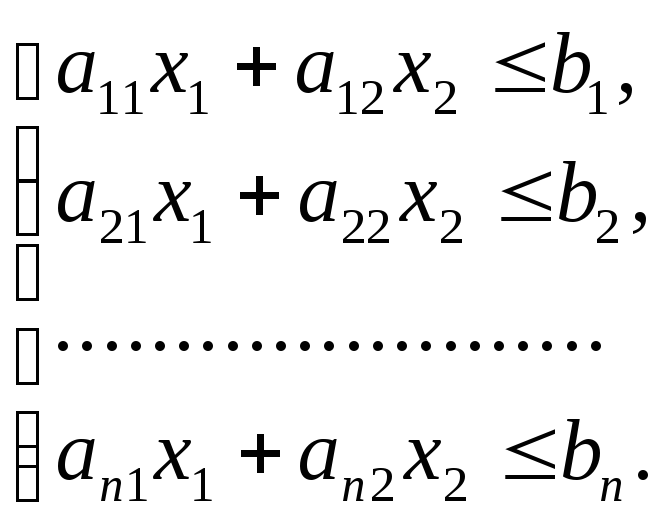

.

Неравенство определяет на плоскостиполуплоскость. Для ее определения построим границу полуплоскости – прямую(удобнее всего ее строить по точкам пересечения с осями координат). Чтобы определить, какую из полуплоскостей надо взять, берется произвольная точкавне прямой (чаще всего точка) и ее координаты подставляются в неравенство. Если неравенство выполняется, то берут полуплоскость, содержащую точку; если не выполняется – не содержащую точку. Область , полученная пересечениями полуплоскостей, определенных для каждого из неравенств системы (1.5.1), (1.5.2), и лежащая в первой четверти, и есть область допустимых значений.

После этого строится линия уровняфункции цели. Для этого сначала построим нормальный вектори, затем, перпендикулярную ему прямую, проходящую через точку(рис.1.5.1). Векторуказывает направление увеличения функции цели. Прямаяназываетсяопорной, если она имеет хотя бы одну общую точку с областью и вся область лежит по одну сторону от. Далее эта прямая передвигается по направлению векторапараллельно самой себе.

Если имеются две опорные прямые, то принимает иизначения (на одной из прямых, на другой -). Если имеется одна опорная прямая, топринимает на данной областиилии не ограничена сверху или снизу соответственно, в зависимости от вида области. Если опорных прямых нет, тоне ограничена и сверху и снизу.

Пример. Завод может производить два вида болтов для крепления колес автомобилей. Для каждого вида болтов должно последовательно использоваться четыре разных группы оборудования, имеющегося в следующих количествах: оборудования группы А – 24, группы В – 16, группы С – 32, и группы D – 24 единицы.

При существующей на заводе технологии, на производство единицы продукции первого вида требуется занять: оборудования группы А – 2, группы В – 1, С – 4 и группы D – 0 единиц.

Техническими коэффициентами при производстве продукции второго вида будут 2,2,0 и 4.

Известно, что единица продукции первого вида дает заводу прибыль 4руб., а второго – 6руб. Сколько единиц продукции каждого вида должен производить завод, чтобы получить наибольшую прибыль?

Запишем исходные данные задачи в форме таблицы.

Группы оборудования	Технические коэффициенты		Общее количество оборудования
	первый вид продукции	второй вид продукции
А	2	2	24
В	1	2	16
С	4	0	32
D	0	4	24
Прибыль (руб./ед. прод.)	4	6

Обозначим через количество единиц продукции каждого вида, которое будет производить завод. Тогда экономико-математическая модель задачи будет иметь вид переопределенной системы неравенств с двумя неизвестными:

, .

Целевая функция будет иметь следующее выражение:

.

Теперь наша задача математического программирования имеет законченный вид.

Далее в прямоугольной системе координат изобразим полученную математическую модель задачи.

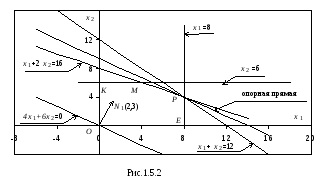
Построим многоугольник допустимых решений (рис.1.5.2).

Проведем в системе координат прямые, координаты точек которых характеризуют максимальное использование оборудования всех групп:,,,. Взяв какую-нибудь точку, например, начало координат, установим, какую полуплоскость определяет соответствующее уравнению неравенство. В результате пересечения полуплоскостей получим некоторый многоугольник, представляющий собой геометрическое место точек, координаты которых определяютвозможный при данных условиях производства вариант плана выпуска продукции. Любая точка, лежащая за пределами многоугольника , своими координатами покажет невозможность выполнения такого плана, так как он не будет обеспечен необходимым производственным оборудованием.

Оптимальное решение достигается при максимальном использовании производственного оборудования. Оно определяется координатами точек, лежащих на границах многоугольника , и в первую очередь, координатами точек, являющихся вершинами многоугольника, так как координаты вершин многоугольника определяют области возможного решения производственной программы, при которой одна, две группы оборудования или более будут использованы полностью.

Найдем точку области допустимых решений, координаты которой соответствуют оптимальному решению, графическим путем. Для этого строим нормальный радиус-вектор или вектор меньшей длины, координаты которого пропорциональны координатам вектора, и через точкупроводим прямую, перпендикулярную ему. Построенную прямуюперемещаем параллельно самой себе в направлении вектора. Прямые, параллельные первоначально полученной прямой, называютсялиниями уровня доходности. Удаляясь от начала координат в направлении вектора , то есть увеличивая значение целевой функции, можно найти такую прямую, которая будет касаться только одной вершины выпуклого множества возможных решений. Очевидно, что будет вершина многоугольника, наиболее удаленная от линии уровня. Координаты этой вершины и покажут оптимальное решение задачи на.

Из рис. 1.5.2 следует, что опорной, по отношению к многоугольнику решений , эта прямая становится в точке, где функцияпринимает максимальное значение. Точкалежит на пересечении прямыхи. Координаты точкиопределяются из решения системы этих уравнений.

Наилучшая производственная программа состоит в выпуске первого вида продукции единиц и второго вида продукцииединицы. При этом максимальная прибыль будет 56руб.

Легко проверить, что любая другая программа выпуска будет менее выгодна.