Glava_5

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Институт экономики, управления и природопользования СФУ

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

совместна. Т.

r n, r 2,n

.pdf

Скачиваний:

Добавлен:

29.03.2016

Размер:

435.5 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

5. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ.
Определение 5.1. Системой		m линейных уравнений с n неизвестными
называется система:
a11x1 a12 x2			a1n xn b1,
	a22 x2		a2n xn	b2 ,
a21x1	a22 x2		a2n xn	b2 ,	(5.1)
					(5.1)

a x a		x	a x b .
m1 1	m2	2	mn n	m

Определение 5.2. Матрица

основной матрицей системы (5.1).

a		a	a
	11	12	1n
	a	a	a
A
	21	22	2n


	a	a	a

	m1	m2	mn

называется

Определение 5.3. Матрица

неизвестных.

X x , x		,	, x	T

1	2		n

называется столбцом

Определение

свободных членов.

Тогда систему

	B b1,b2 ,	T
5.4. Матрица	B b1,b2 ,	,bn	называется
(5.1) можно записать в матричном виде:
AX B

столбцом

(5.2)

		a		a	a	b
			11	12	1n	1
			a	a	a	b
			a	a	a	b
Определение 5.5. Матрица	A		21	22	2n	2
Определение 5.5. Матрица	A


			a	a	a	b
			a	a	a	b
			m1	m2	mn	m

расширенной матрицей системы (5.1).

называется

Определение 5.6. Столбец

X x , x		,	, x	T

1	2		n

называется решением

системы (5.1), если при подстановке его в (5.2) получаем матричное тождество.

Системы бывают несовместные и совместные.

Совместные системы бывают определенными и неопределенными.

Определение 5.7. Система (5.1) называется совместной (совместимой),

если имеет хотя бы одно решение, в противном случае она несовместна

(несовместима).

Определение 5.8. Совместная система называется определенной, если она имеет единственное решение, в противном случае она неопределенная.

Определение 5.9. Система (5.2) называется однородной, если противном случае она неоднородна.

, в

Теорема 5.1 (Кронекера – Капелли).

Система (5.1) совместна тогда и только тогда, когда ранг расширенной матрицы равен рангу основной матрицы, то есть r( A) r( A) .

Совместная система будет определенной, если ранг матрицы равен числу неизвестных, то есть r( A) n .

Совместная система будет неопределенной, если ранг матрицы меньше

числа неизвестных, то есть

r( A) n .

Методы решения систем линейных уравнений.

Метод Крамера.

Рассмотрим случай,

когда

m n , то есть основная матрица системы (5.1)

квадратная.

Итак,

если

A 0

(матрица невырожденная ), то решение системы

(5.1) можно найти по формулам Крамера:

, x2

Здесь

определители, которые получаются из

заменой

, а

i -го столбца столбцом свободных членов.

					x		2x
Пример 5.1. Найти	решение системы					1	2
Пример 5.1. Найти	решение системы					x	3x
						x	3x
						1	2
Крамера.
Решение. Найдем	1	2	5,	1	2		5,
	1	3	1	4	3
			1

Отсюда	x			x			1
			1 1,			2
	1			2

			2( 1)	1
Проверка		1			Система решена верно.

		1 3( 1) 4

1	по	формулам
4	по	формулам
4
2	1	1	5;
	1	4

Матричный метод.
Рассмотрим случай, когда	m n , то есть основная матрица

(5.1) квадратная.

В матричном виде система записывается AX B . Пусть A 0 , тогда существует A 1 . Тогда X A 1B .

системы

		5.2.		Найти				решение			системы			x		2x		1,	матричным
Пример		5.2.		Найти				решение			системы				1		2		матричным
															x1 3x2 4
методом.
Выпишем		A		1		2		, B		1
Выпишем		A				3		, B		.
				1		3				4
Найдем	A		1		2	5 0			(можно решать матричным методом).
Найдем	A					5 0			(можно решать матричным методом).
			1	3
				1								1	3			2
Найдем A 1					A		. Получаем				A 1			1		1	.
Найдем A 1				A	A		. Получаем				A 1	5					.
				A								5

			x	1		1	3	2	1	1	5	1
Тогда решение			1		B
		X	x	A		5	1	1	4	5	5	1	.

			2
Отсюда,	x1 1, x2 1.

Метод Гаусса.

Методом Гаусса можно решать невырожденные и вырожденные системы и системы с прямоугольными матрицами. Кроме того, этот метод требует меньше вычислительной работы и в настоящее время является самым эффективным.

Определение 5.10. Две системы линейных уравнений называются

эквивалентными (равносильными), если

1)все решения одной являются решениями другой и наоборот;

2)обе несовместны.

Эквивалентные преобразования систем:

1)строки расширенной матрицы системы можно менять местами;

2)любую строку расширенной матрицы системы можно умножить на

произвольное число

и сложить с другой строкой;

3) в расширенной матрице можно менять местами столбцы с коэффициентами неизвестных.


После этих преобразований системы можем получить такую строку в
расширенной матрице системы – 0,0,	,0 c . Тогда:
а) если c 0, то это говорит о линейной зависимости строк матрицы A .
б) если c 0 , то система несовместна.		Такая строка означает, что в
эквивалентной системе есть уравнение вида		0 x1 0 x2	0 xn c , чего

быть не может.

Метод Гаусса (прямой ход)

Выпишем расширенную матрицу системы (5.1) и путем эквивалентных преобразований приведем ее к трапецеидальному виду. Возможны следующие варианты.

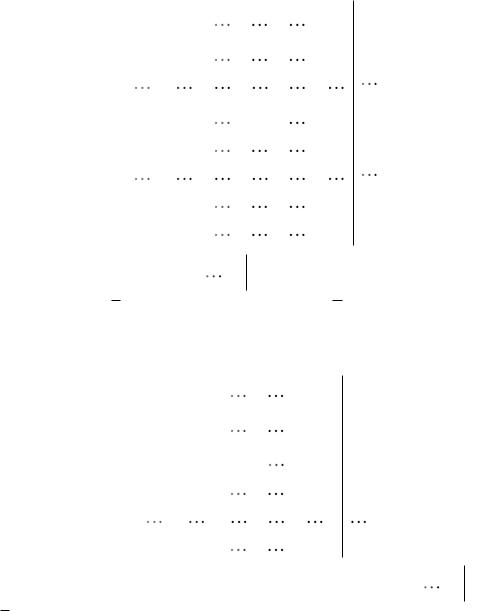
1. Получим матрицу вида

a11

Здесь есть строка вида

Или, r A r, r A r

a12 a22

		0	a	rr
				rr
		0
		0
		0
				k
	0	0	0 b
1; отсюда				r

a	b
a	1
1n	b
a	b
a	2
2n

	br
a	br	.
rn		.
0	0


0	bk
0	bk
0	0
0	0
, значит система несовместна.
A r A , следовательно система

несовместна (по теореме Кронекера – Капелли). 2. Получим матрицу вида

Система совместна,

так

как

нет

строки

вида

; или

0 b

r A r A .

Тогда:

а) если r n , то система имеет единственное решение;

б) если r n , то система имеет бесконечное множество решений.

Решения системы находят обратным ходом метода Гаусса. Обратный ход

а) r n .

Выписываем последнее уравнение в эквивалентной системе и находим

x	n	. Затем переходим к	n 1 уравнению, подставляя в него	x	n	, находим	x	и
	n				n		n 1

так далее.

б) r n .

Определение 5.11.. Базисным минором матрицы называется отличный от нуля угловой минор, порядок которого равен r .

Первые

неизвестных считаем базисными неизвестными, а остальные

свободными, придавая им следующие значения:

xr 1 c1, xr 2 c2 ,	, xn cn r .
Далее последовательно выражаем базисные неизвестные через
свободные.
Из последнего ненулевого уравнения находим xr			и т. д.
Получаем общее решение системы X x1, x2			T
Получаем общее решение системы X x1, x2		,..., xr ,c1,c2 ,...,cn r .
Придавая c1,c2 ,	,cn r любые значения из	R ,	получим бесконечное

множество частных решений системы.

Пример 5.3. Найти решение системы

	2x	x		x		2,
	1		2		3
x	3x		x		6,
x	3x		x		6,
1		2		3
x 2x				2x			2
x 2x				2x			2
	1		2		3

методом

Гаусса.

Решение. Прямой ход.

Преобразуем эквивалентными преобразованиями расширенную матрицу системы.

			2				1	1			2			1				3	1		6				1		3	1	6
A					1		3	1		6					1			2	2		2					0	5	1	4
A					1		3	1		6					1			2	2		2					0	5	1	4

				1			2	2			2					2		1	1		2					0	7	3	10
				1			2	2			2					2		1	1		2					0	7	3	10

	1				1								1				1		3		6
	1				1			3		6				0				1	5		4
														0				1	5		4
			0			1 5				4				0				0 22			22
			0			3	7			10
																x1		x3	x2		bi
																x1		x3	x2		bi
Итак,					r A r						3, система совместна,											т.			к.,		r n 3 ,		то система
Итак,					r A r				A		3, система совместна,											т.			к.,		r n 3 ,		то система
имеет единственное решение.
Метод Гаусса (обратный ход)
Запишем эквивалентную систему:
x		x				3x		6,
1					3		2
		x			5x 4,						Из последнего уравнения											x		1, из второго уравнения
			3				2																2
	22x2						22.
	22x2						22.
x 1, из первого уравнения													x		2.
3													1
Ответ.						x1 2, x2					1,	x3	1.
Пример 5.4. Найти решение системы																					2 y x 3,						методом Гаусса.
Пример 5.4. Найти решение системы																											методом Гаусса.
																				2x 4 y 5.
																		49

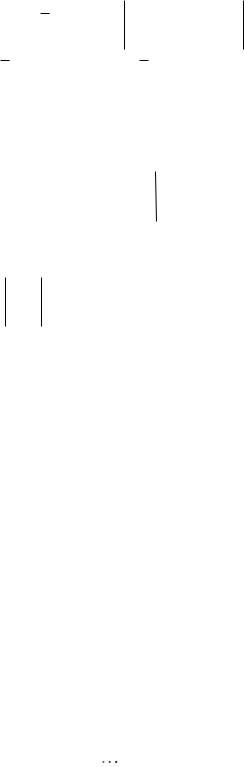
	1		2	3	1		2
Решение: A		2	4	5		0	0


r A 1, r A 2,	r A r A .

Ответ. Решений нет.

Пример 5.5. Найти решение системы

3		Система несовместна, т. к.,
11

x		x	x	1,	методом Гаусса.
	1	2	3		методом Гаусса.
		x2 x3		0.

бесконечное множество решений).

Так	как r A r		2 , то	система
		A
3 , то	система неопределенная			(имеет

Итак,

1	1
0	1

базисный минор, а

x ,	x
1	2

базисные неизвестные,

x
3

свободная неизвестная.

Положим x3 c . Из последнего уравнения, x2

Из первого уравнения, x1	1 2c .
Итак, x1 1 2c , x2 c	,	x3 c ,	где	c R ;
Х 1 2c, c,c T . Придавая c		любые значения из

множество частных решений системы. Проверка общего решения:

c 0, x2 c .

общее решение системы: R , получим бесконечное

1 2c c c 1

	c c 0

Положим, c 1, Частное решение Х (c

1	1	Решение найдено верно.
	0	Решение найдено верно.
0	0

тогда получим частное решение: x1 3,

1) 3, 1,1 T .

, x3 1.

Однородные системы линейных уравнений

Определение 5.12. Система вида AX 0 называется однородной.

Однородная система всегда совместна. Очевидно, что у нее есть решение x1 0, x2 0, , xn 0 . Это решение называется нулевым или

тривиальным.

Возможны два случая.

1.Если число неизвестных равно рангу основной матрицы, то есть r A n , то система имеет единственное нулевое решение.

2.Если r n , то система имеет бесконечное множество решений и общее решение системы находится методом Гаусса.

Среди решений однородной системы уравнений, являющихся

n -

мерными векторами, можно выбрать конечную максимальную линейно независимую систему решений (векторов). Т. е., любое другое решение будет являться линейной комбинацией этих решений.

Определение 5.13. Любая максимальная линейно независимая система решений однородной системы уравнений называется фундаментальной системой решений (Ф.С.Р.).

Теорема 5.2. Фундаментальная система решений

однородных уравнений состоит из ( n r ) решений E1 число неизвестных системы, а r – ранг матрицы системы.

системы

, E	,..., E
2	n

линейных r , где n −

Придавая свободным неизвестным значения

получаем Ф.С.Р. − E1, E2 ,..., En r .

1	0	0 ...
0	1	0 ...
... ... ... ...
0	0	0 ...

0
0
0
		(n
...

1
1

Пример 5.6. Найти общее решение однородной системы уравнений и

			x x			x	2x		0,
фундаментальную систему решений:				1	2	3	4			.
фундаментальную систему решений:				3x 2x 5x				0.		.
				3x 2x 5x				0.
					1	3	4
Решение. Выпишем	матрицу				системы				и	приведем ее к
1		1	1		2	1	1		1	2	, r 2 .
трапецеидальному виду: A											, r 2 .
	3	0	1		5	0	3		1	1

	Базисный минор											1		1		, базисные неизвестные										x1 и	x2 , свободные
	Базисный минор											0	3			, базисные неизвестные										x1 и	x2 , свободные
												0	3
неизвестные			x3 c1 ,					x4 c2 .
	Выразим базисные неизвестные через свободные. Из последней строки
матрицы:
		3x c c					0 ,							c c
											x			1				2		.	Из первой строки матрицы найдем x .
											x									.	Из первой строки матрицы найдем x .
		2	1			2						2				3											1
																3
x x		c 2c			0		,		x			c 2c							c1 c2 ,			x	2	c 1	2	c .	Итак, общее
x x		c 2c			0		,		x			c 2c							c1 c2 ,			x		c 1		c .	Итак, общее
1	2	1	2						1				1				2				3	1	3 1		3	2
решение Х				2		c1		5				1			1
									c2	,			c1				c2	,c1			,c2 .
				3				3	c2	,		3	c1		3		c2	,c1			,c2 .
				3				3				3			3

Ф.С.Р. состоит из	n r 4 2 2	решений. Придавая	c	и c	значения
			1		2
1, 0 и 0, 1, получаем:

E2	5	;	1		, E1	2		1			X c1E1 c2 E2 .
E2	3	;	3	;0;1	, E1	3	;	3	;1;0	и	X c1E1 c2 E2 .
	3		3			3		3

Пусть дана неоднородная система уравнений	AX
Определение 5.14. Однородная система	AX
приведенной системой для неоднородной системы.

B .0

называется

5.1. Доказать совместность и найти решение систем линейных уравнений: а) методом Гаусса; б) методом Крамера;

в) методом обратной матрицы.

x 2 y z 4
		5 y 3z 1;
3x		5 y 3z 1;
	2x	7 y z 8
	2x	7 y z 8

x y z 1
		y 2z 3;
2x		y 2z 3;
	3x	3z 5
	3x	3z 5

2x 2x				x	x		4
	1		2	3		4
	4x		3x	x	2x			6
	4x		3x	x	2x			6
	1		2	3			4
			5x	3x		4x			12
8x			5x	3x		4x			12
	1		2	3			4
	3x		3x	2x		2x			6
	3x		3x	2x		2x			6
	1		2	3			4

;

2x 4 y 3z 1

2)x 2 y 4z 3 ;3x y 5z 2x y z 2

4)2x 2 y 2z 4 ;3x y z 5

	2x			3x		11x 5x					2
			1		2			3		4
		x	x		5x			2x		1

6)		1		2		3		4
		2x		x		3x		2x		3

			1		2		3		4
	x		x		3x			4x		3
		1		2		3		4

5.2. Найти общее решение, одно частное решение и фундаментальную систему решений однородных систем линейных уравнений.

1)3x1

4x11

3)	x1 x2
5)	0 x1

x2 4x3 0 5x2 7x3 0 ; 5x2 6x3 0

x3	0	;
0 x	0 x		0 x
2		3	4

;

	2x x			5x	7x	0
		1	2	3	4
2)			2x2 7x3 5x4				0 ;
	4x1
		2x	x	x 5x		0

		1	2	3	4
4)	x1 x2 x3 x4 0					;
6)	9x1		21x2 15x3 5x4 0					.

	12x1 28x2				20x3		7x4	0

5.3. Исследовать на совместность и найти решения систем:

x y z 1

1) 2x y z 2 ;3x 2 y 2z 3

5.4. Определить при каких а и b система

x y z 2

2)3x 2 y 3z 5 .2x 3y 4z 3

3x 2 y z b5x 8 y 9z 3 :2x y аz 1

1) определена; 2) несовместна; 3) не определена.

	ax y z 1
5.5. Определить при каких а система			:
	x ay z 1
		x y аz 1


1) определена; 2) несовместна; 3)	не определена.

ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ №2

1.Найти определитель: а) разложением по строке (столбцу); б) методом Гаусса.

	1
	3
1.	5
	1
	3
	2
		2
3.		1
	1
	4
		1
		1
		0
5.		2
		2
		2

2	1	1
1	1	1
4	1	0
1	1	0
3	3	3
2	1	1
3	1	1
0	1	0
1	1	0
4	4	4
2	1	1
2	1	1
3	3	0
2	2	1
2	2	2

1
1
0	;
1
1

1
1
0	;
1
2
1
1
1
0	;
1
1

	4	2	1	1
	1	0	1	1
2.	0	1	3	0
	1	1	1	2
	1	1	1	1
	2	2	1	1
	1	2	1	1
4.	2	1	1	0
	1	1	1	0
	3	3	3	3
	2	2	1	1
	1	2	1	1
6.	2	3	3	0
	0	0	0	3
	3	3	3	3

1
1
0	;
1
1

1
1
0	;
1
1

1 0 ; 1

5	2	1	1
1	1	1	1
2	1	2	0
1	1	1	0
2	2	2	2
3	2	1	1
2	2	1	1
2	1	1	0
4	4	4	3
2	2	2	2

11 0 0 1

1 0 1

;

	2	2	1	1	1
	1	2	1	1	1
8.	0	1	1	0	0	;
	1	1	1	0	1
	3	3	3	3	1
	3	2	1	1	1
	3	3	1	1	1
10.	1	0	1	0	0	;
	4	4	4	3	1
	2	2	2	2	1

	3
	1
11.	2
	1
	3
	5
	5
	3
13.	1
	3
	3
	2
	2
	1
15.	4
	4
	3
	5
	2
17.	0
	1
	2
	4
	4
19.	1
	1
	1
	2
	2
	0
21.	3
	5
	3

2	1	1
1	1	1
1	2	0
1	1	1
3	3	3
2	1	1
1	1	1
0	1	0
3	3	4
3	3	3
2	1	1
0	1	1
3	1	0
4	4	3
3	3	3
2	1	1
0	1	1
1	3	0
1	1	4
2	2	2
2	1	1
3	1	1
2	1	0
1	1	0
1	1	1
2	1	1
1	1	1
2	1	0
5	5	4
3	3	3

11 0 1 2 11 0 11 11 0 12 11 0 1 0 11 0 11 11 0 11

;

		2	2	1	1	1
		2	1	1	1	1
12.	5		4	1	0	0 ;
		1	2	0	4	1
	1		1	1	1	1
		4	2	1	1	1
		3	2	1	1	1
14.		2	3	3	0	0	;
		3	3	3	0	1
		1	1	1	1	1
		2	2	1	1	1
		0	1	1	1	1
16.		1	2	3	1	0	;
		1	1	1	4	1
		2	2	2	2	0
		2	2	1	1	1
		0	1	1	1	1
18.		0	1	2	0	0	;
		1	1	1	3	1
		3	3	3	3	2
		2	2	1	1	1
		1	2	1	1	1
20.		2	1	1	0	0	;
		4	4	4	3	1
		2	2	2	2	1
		2	2	1	1	1
		1	2	1	1	1
22.		0	1	1	0	0	;
		1	1	1	2	1
		1	1	1	1	1

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.11.2018176.13 Кб92КР производственныемощности.doc
#
04.05.2019129.54 Кб73-4 занятие. Духовная сфера общества.doc
#
04.05.2019132.61 Кб15-6-7 занятие. Человек. Деятельность. Социализа...doc
#
19.11.20191.18 Mб1dokumenty.docx
#
27.09.2019118.7 Кб13FILOSOFIYa.docx
#
29.03.2016435.5 Кб5Glava_5.pdf
#
29.03.2016337.2 Кб36Glava_9.pdf
#
17.04.2019170.5 Кб0Gosudarstvennoe_upravlenie-Dnevnoe.doc
#
29.03.20161.75 Mб88i-917692.pdf
#
15.04.201998.3 Кб3IAS 36.doc
#
15.04.2019107.52 Кб3IAS 38.doc

	4	2	1	1
	1	0	1	1
2.	0	1	3	0
	1	1	1	2
	1	1	1	1
	2	2	1	1
	1	2	1	1
4.	2	1	1	0
	1	1	1	0
	3	3	3	3
	2	2	1	1
	1	2	1	1
6.	2	3	3	0
	0	0	0	3
	3	3	3	3

2	1	1
1	1	1
1	2	0
1	1	1
3	3	3
2	1	1
1	1	1
0	1	0
3	3	4
3	3	3
2	1	1
0	1	1
3	1	0
4	4	3
3	3	3
2	1	1
0	1	1
1	3	0
1	1	4
2	2	2
2	1	1
3	1	1
2	1	0
1	1	0
1	1	1
2	1	1
1	1	1
2	1	0
5	5	4
3	3	3

		2	2	1	1	1
		2	1	1	1	1
12.	5		4	1	0	0 ;
		1	2	0	4	1
	1		1	1	1	1
		4	2	1	1	1
		3	2	1	1	1
14.		2	3	3	0	0	;
		3	3	3	0	1
		1	1	1	1	1
		2	2	1	1	1
		0	1	1	1	1
16.		1	2	3	1	0	;
		1	1	1	4	1
		2	2	2	2	0
		2	2	1	1	1
		0	1	1	1	1
18.		0	1	2	0	0	;
		1	1	1	3	1
		3	3	3	3	2
		2	2	1	1	1
		1	2	1	1	1
20.		2	1	1	0	0	;
		4	4	4	3	1
		2	2	2	2	1
		2	2	1	1	1
		1	2	1	1	1
22.		0	1	1	0	0	;
		1	1	1	2	1
		1	1	1	1	1

	4	2	1	1
	1	0	1	1
2.	0	1	3	0
	1	1	1	2
	1	1	1	1
	2	2	1	1
	1	2	1	1
4.	2	1	1	0
	1	1	1	0
	3	3	3	3
	2	2	1	1
	1	2	1	1
6.	2	3	3	0
	0	0	0	3
	3	3	3	3

2	1	1
1	1	1
1	2	0
1	1	1
3	3	3
2	1	1
1	1	1
0	1	0
3	3	4
3	3	3
2	1	1
0	1	1
3	1	0
4	4	3
3	3	3
2	1	1
0	1	1
1	3	0
1	1	4
2	2	2
2	1	1
3	1	1
2	1	0
1	1	0
1	1	1
2	1	1
1	1	1
2	1	0
5	5	4
3	3	3

		2	2	1	1	1
		2	1	1	1	1
12.	5		4	1	0	0 ;
		1	2	0	4	1
	1		1	1	1	1
		4	2	1	1	1
		3	2	1	1	1
14.		2	3	3	0	0	;
		3	3	3	0	1
		1	1	1	1	1
		2	2	1	1	1
		0	1	1	1	1
16.		1	2	3	1	0	;
		1	1	1	4	1
		2	2	2	2	0
		2	2	1	1	1
		0	1	1	1	1
18.		0	1	2	0	0	;
		1	1	1	3	1
		3	3	3	3	2
		2	2	1	1	1
		1	2	1	1	1
20.		2	1	1	0	0	;
		4	4	4	3	1
		2	2	2	2	1
		2	2	1	1	1
		1	2	1	1	1
22.		0	1	1	0	0	;
		1	1	1	2	1
		1	1	1	1	1

	4	2	1	1
	1	0	1	1
2.	0	1	3	0
	1	1	1	2
	1	1	1	1
	2	2	1	1
	1	2	1	1
4.	2	1	1	0
	1	1	1	0
	3	3	3	3
	2	2	1	1
	1	2	1	1
6.	2	3	3	0
	0	0	0	3
	3	3	3	3

2	1	1
1	1	1
1	2	0
1	1	1
3	3	3
2	1	1
1	1	1
0	1	0
3	3	4
3	3	3
2	1	1
0	1	1
3	1	0
4	4	3
3	3	3
2	1	1
0	1	1
1	3	0
1	1	4
2	2	2
2	1	1
3	1	1
2	1	0
1	1	0
1	1	1
2	1	1
1	1	1
2	1	0
5	5	4
3	3	3

		2	2	1	1	1
		2	1	1	1	1
12.	5		4	1	0	0 ;
		1	2	0	4	1
	1		1	1	1	1
		4	2	1	1	1
		3	2	1	1	1
14.		2	3	3	0	0	;
		3	3	3	0	1
		1	1	1	1	1
		2	2	1	1	1
		0	1	1	1	1
16.		1	2	3	1	0	;
		1	1	1	4	1
		2	2	2	2	0
		2	2	1	1	1
		0	1	1	1	1
18.		0	1	2	0	0	;
		1	1	1	3	1
		3	3	3	3	2
		2	2	1	1	1
		1	2	1	1	1
20.		2	1	1	0	0	;
		4	4	4	3	1
		2	2	2	2	1
		2	2	1	1	1
		1	2	1	1	1
22.		0	1	1	0	0	;
		1	1	1	2	1
		1	1	1	1	1