2 4 5 2

2 1 29 10

3

2 12 39

7 0

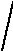
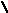0 15 39

1 0 5 4 2 5

0 17 8

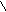7 8

8 8

3 0 23 31

8 6 0

t _p 31

N R

t _n

Рис. 2.10 - Сетевой график

Находим параметры по событиям.

1) Ранний срок наступления события i, t_p ( i ).Это максимальный путь от начального события до i - го события:

t_p( 1 ) = 0; t_p( 2 ) = t_1,2 = 2

В третье событие входят 2 работы : (2,3) и (1,3), значит

t_p(3)=max{t_p(2) + t_2,3 ; t_p(1) + t_1,3}=max{2+5, 8}= 8

В четвертое событие входит одна работа (3,4)

t_p(4) = t_p(3)+t_3,4 = 8+7=15

В пятое событие входят 2 работы : (2,5) и (4,5), значит

t_p(5)=max{t_p(2) + t_2,5 ; t_p() + t_4,5}=max{2+4, 15+12}= 27

В шестое событие входят две работы : (4,6) и (3,6), значит

t_p(6)=max{t_p(4) + t_2,5 ; t_p(3) + t_3,6}=max{15+4, 8+23}= 31

В седьмое событие входят три работы : (5,7); (4,7); (6,8) значит

t_p(7)=max{t_p(5) + t_5,7 ; t_p(4) + t_4,7; t_p(6) + t_6,7}=

max{5+5, 27+10,31+8}= 39

2) Поздний срок наступления события i, t_n ( i ) — это разность между продолжительностью максимального пути l_max и пути наибольшей продолжительности от данного события i до конечного события.

Рассчитывается t_n ( i ) по обратной схеме t_p ( i ). Значит, расчет начинаем от конечного события, ориентируемся на выходящие работы, берем минимум разности.

Для конечного события

t_n(7) = t_p(7)=39

Из шестого события выходит одна работа : (6,7)

t_n(6) = t_n­­­­­­­_­(7) - t_6,7 = 39 - 8 = 31

Из пятого события выходит одна работа : (5,7)

t_n(5) = t_n­­­­­­­­(7) - t_5,7 = 39 - 10 = 29

Из четвертого события выходит 3 работы : (4,5);(4,6);(4,7)

t_n(4) = min{ t_n­­­­­­­_­(5) - t_4,5 ; t_n­­­­­­­_­(6) - t_4,6 ; t_n­­­­­­­_­(7) - t_4,7 }=

min{29 - 12; 31 - 4; 39 - 5}= 17

Из третьего события выходит 2 работы : (3,4);(3,6)

t_n(3)=min{t_n­­­­­­­_­(4) - t_3,4 ; t_n­­­­­­­_­(6) - t_3,6}=min{17 - 7;31 - 23}= 8

Из второго события выходит 2 работы : (2,5);(2,3)

t_n(2)=min{t_n­­­­­­­_­(5) - t_2,5 ; t_n­­­­­­­_­(3) - t_1,3}=min{8 - 5;29 - 4}= 3

Из начального события выходит 2 работы : (1,2);(1,3)

t_n(1)=min{t_n­­­­­­­_­(2) - t_1,2 ; t_n­­­­­­­_­(3) - t_1,3}=min{3 - 2;8 - 8}= 0

Для начального события должно выполняться условие:

t_p( 1 ) = t_n ( 1 ) = 0 .

3) Находим резерв времени по событиям:

R( i ) = t_n( i ) - t_p( i ).

R(1) = 0; R(2) = 3-2 =1; R(3) = 8-8 = 0;

R(4) = 17-15 = 2; R(5) = 29-27 = 2; R(6) = 31-31 = 0;

R(7) = 39-39 = 0.

4) Критический путь проходит по событиям с нулевым резервом времени R( i ) = 0, т.е. 1, 3, 6, 7, (выделено на графе). Длина критического пути L_кр — это самый длинный путь от начального события до конечного :

L_кр = t_p(7) = 39.

Рассчитаем необходимые параметры по работам.

5) Ранний срок окончания работы ( i , j ) :

t_p.o( i , j )=t_p( i ) + t_i,j

t_p.o(1,2)=t_p(1) + t_1,2 = 0+2 = 2;

t_p.o(1,3)=t_p(1) + t_1,3 = 0+8 = 8;

t_p.o(2,3)=t_p(2) + t_2,3 = 2+5 = 7;

t_p.o(2,5)=t_p(2) + t_2,5 = 2+4 = 6;

t_p.o(3,4)=t_p(3) + t_3,4 = 8+7 = 15;

t_p.o(3,6)=t_p(3) + t_3,6 = 8+23 = 31;

t_p.o(4,5)=t_p(4) + t_4,5 = 15+12 = 27;

t_p.o(4,6)=t_p(4) + t_4,6 = 15+4 = 19;

t_p.o(4,7)=t_p(4) + t_4,7 = 15+5 = 20;

t_p.o(5,7)=t_p(5) + t_5,7 = 27+10 = 37;

t_p.o(6,7)=t_p(6) + t_6,7 = 31+8 = 39;

6) Поздний срок наступления окончания работы ( i , j ):

t_n.o (1,2) = t_n(2) = 3; t_n.o (2,3) = t_n(3) = 8;

t_n.o (1,3) = t_n(3) = 8; t_n.o (2,5) = t_n(5) = 29;

t_n.o (3,4) = t_n(4) = 17; t_n.o (4,5) = t_n(5) = 29;

t_n.o (3,6) = t_n(6) = 31; t_n.o (4,6) = t_n(6) = 31;

t_n.o (5,7) = t_n(7) = 39; t_n.o (4,7) = t_n(7) = 39.

t_n.o (6,7) = t_n(7) = 39;

7) Полный резерв времени работы i , j — это время, на которое можно увеличить продолжительность данной работы, не изменяя при этом продолжительность критического пути L_кр.

R_n( i , j ) = t_n ( j ) - t_p( i ) - - t_i,j;

R_n(1,2) = t_n (2) - t_p(1) - t_1,2 = 3-0-2 = 1;

R_n(1,3) = t_n (3) - t_p(1) - t_1,3 = 8-0-8 = 0;

R_n(2,3) = t_n (3) - t_p(2) - t_2,3 = 8-2-5 = 1;

R_n(2,5) = t_n (5) - t_p(2) - t_2,5 = 8-2-4 = 2;

R_n(3,4) = t_n (4) - t_p(3) - t_3,4 = 17-8-7 = 2;

R_n(3,6) = t_n (6) - t_p(3) - t_3,6 = 31-8-23 = 0;

R_n(4,5) = t_n (5) - t_p(4) - t_4,5 = 29-15-12 = 2;

R_n(4,6) = t_n (6) - t_p(4) - t_4,6 = 31-15-4 = 12;

R_n(5,7) = t_n (7) - t_p(5) - t_5,7 = 39-27-10 = 2;

R_n(6,7) = t_n (7) - t_p(6) - t_6,7 = 39-31-8 = 0;

Работа (4,7) имеет большой резерв времени (12), значит можно с этой работы снять на данном этапе ресурсы и перебросить их на работы лежащие на критическом пути. Аналогично, работы (2,5),(3,4),(4,5),(5,7) имеют резерв времени равный 2 . Работу (2,3) считаем под критической, а работы с нулевым резервом времени — критические. На рисунке критический путь отмечен жирной линией.

2.8. Оптимизация на сетях.

Пусть S - произвольная, частично ориентированная сеть, каждому ребру u которой приписанное неотъемлемое число c(u) - пропускная способность. Потоком в сети S называется пара (f, w), где w - некоторая ориентация всех неориентированных ребер сети, а f(u) -заданная на множестве всех ребер функция с не отрицательными значениями, которые не превосходят пропускных способностей, и такая, что в каждой внутренней вершине  выполняется закон Кірхгофа, соответственно которой сумма значений потока по ребрам, которые входит в вершину, равно сумме потоков по ребрам, которые выходит с вершины . Иными словами, для f(u) выполняются условия:

0  f(u)  c(u) для всех вершин сети;

R() = 0 для всех внутренних вершин, где

а () (соответственно '()) - множество всех ребер, которое выходят из  (соответственно входящих в ) при ориентации w.

Поскольку сумма значений R() по всем вершинах сети, включая полюса, равно нулю (каждое ребро есть исходным для одной вершины и входным для другой), то R(_s) = - R(_s). Значение R = R(_s) называется величиной потока.

Рассмотрим задачу определения максимального значения Rmax потока через сеть S при заданных значениях пропускных способностей. Ответ может быть получен в терминах сечений сети.

Сечением сети называется множество ребер, при удалении которых сеть становится несвязной, причем полюса попадают в разные компоненты связности. В сети на рис.2.11 примерами сечений есть {d, e, f}, {b, c, e, g, h}, {d, g, h, i}.

5

7 a d h 2

_S 2 c 4 e 3 g _S

3 b 4 i

1

f

Рис. 2.11 - Задача максимального потока

Сечение называется простым, если при удалении какого-нибудь его ребра, оно перестает быть сечением. Да, сечения {d, e, f} и {b, c, e, g, h} есть простыми, а сечение {d, g, h, i} не является таким. По-видимому, что для каждого ребра простого сечения можно указать цепь, что проходить через это ребро, но не проходит через иные ребра данного сечения.

Если в связной сети выполняется простое сечение, то сеть распадается ровно на две части: левую часть, что содержит _S, и правую часть, что содержит _S. Каждое ребро простого сечения связывает вершины с разных частей. Будем называть ребро сечения прямым, если оно в сети не ориентированное или ориентирован слева по правой сторону, и обратным в противном случае. Будет ориентированное ребро прямым или обратным, зависит от выбора сечения. Так, в примере ребро е в сечениях {d, e, f} и {b, c, e, g, h} - обратное, а в сечении {a, c, e, g, i}- прямое.

Каждому простому сечению W припишем пропускную способность c(W), равную сумме пропускных способностей всех его прямых ребер. В примере на рис.2.11 сечение {d, e, f} имеет пропускную состоятельность 5+1=6, а сечение {b, c, e, g, h} - 3+2+3+2=10.

Теорема о максимальной пропускной состоятельность сети сформулированная Фордом и Фалкерсоном в таком виде: Максимальный размер потока Rmax через сеть S равно минимальной с пропускных способностей c_min ее простых сечений. Доказательство этой теоремы приведено в [2]. Эта теорема положена в основу задачи определения максимальной пропускной состоятельности сети.

Рассмотрим алгоритм Форда-Фалкерсона определение максимального потока.

Шаг 0. Пусть источники помечены но не просмотрены, а все остальные узлы не помечены.

Шаг 1. Выбрать любой помеченный, но не просмотренный узел i.

Шаг 2. Просмотреть все дуги e (i, j) с пропускной способностью  _е  0, соединяющие узел i с еще не помеченными узлами j. Приписать пометки узлам j и отметить дуги e _j = e = (i, j).Теперь узел i помечен и просмотрен, узлы j помечены, но не просмотрены. Если при этом сток оказался помеченным, то необходимая цепь найдена. В противном случае после просмотра по всем дугам (i, j) перейти к шагу 3.

Шаг 3. Пусть узел i помечен и просмотрен. Перейти к шагу 1 и повторять шаги алгоритма до тех пор, пока не останется помеченных и не просмотренных узлов. На этом поиск максимального потока заканчивается.

Рассмотрим пример.