
Лек1 Парная регрессия и корреляция
.docxЛекция 1 Парная регрессия и корреляция
1.1 Спецификация модели
Ставя цель дать количественное описание взаимосвязей между экономическими переменными, эконометрика прежде всего связана с такими методами статистики, как регрессия и корреляция.
В зависимости от количества факторов (переменных х), включенных в уравнение регрессии, принято различать парную и множественную регрессии.
Парная регрессия представляет собой модель, где среднее значение зависимой (объясняемой) переменной у рассматривается как функция одной независимой (объясняющей) переменной х, т.е. это модель вида
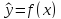
Множественная регрессия представляет собой модель, где среднее значение зависимой (объясняемой) переменной у рассматривается как функция нескольких независимых (объясняющих) переменных х1,х2, …, т.е. это модель вида

Уравнение простой регрессии характеризует связь между двумя переменными, которая проявляется как некоторая закономерность лишь в среднем по совокупности наблюдений.
В уравнении регрессии корреляционная по сути связь признаков представляется в виде функциональной связи, выраженной соответствующей математической функцией. Практически в каждом отдельном случае величина у складывается их двух слагаемых:

где
 – фактическое значение результативного
признака;
– фактическое значение результативного
признака;
 –
теоретическое
значение результативного признака,
найденное исходя из соответствующей
математической функции связи у и х, т.е.
из уравнения регрессии;
–
теоретическое
значение результативного признака,
найденное исходя из соответствующей
математической функции связи у и х, т.е.
из уравнения регрессии;
 – случайная
величина, характеризующая отклонения
реального значения результативного
признака от теоретического, найденного
по уравнению регрессии.
– случайная
величина, характеризующая отклонения
реального значения результативного
признака от теоретического, найденного
по уравнению регрессии.
Запишем
уравнение зависимости
 от
от
 в виде регрессионного уравнения:
в виде регрессионного уравнения:

где  – неслучайная (детерминированная)
величина;
– неслучайная (детерминированная)
величина;
 – случайные величины.
– случайные величины.
 – регрессионные остатки модели
(отклонения модельных данных от
фактических)
– регрессионные остатки модели
(отклонения модельных данных от
фактических)
 – называется объясняемой (зависимой)
переменной [выходной, результирующей,
эндогенной переменной, результативным
признаком]
– называется объясняемой (зависимой)
переменной [выходной, результирующей,
эндогенной переменной, результативным
признаком]
 – называется объясняющей (независимой)
переменной или регрессором [входной,
экзогенной переменной, фактором,
факторным признаком]
– называется объясняющей (независимой)
переменной или регрессором [входной,
экзогенной переменной, фактором,
факторным признаком]
Причины появления в модели случайной величины ε или возмущения:
1) ошибки спецификации модели
Неправильный
выбор математической функции для
 и недоучет в уравнении регрессии
какого-либо существенного фактора, т.е.
использование парной регрессии вместо
множественной.
и недоучет в уравнении регрессии
какого-либо существенного фактора, т.е.
использование парной регрессии вместо
множественной.
2) выборочный характер исходных данных
Ошибки выборки имеют место в силу неоднородности данных в исходной статистической совокупности.
3) ошибки измерения переменных
т.о.
 – случайная величина с некоторой
функцией распределения, которой
соответствует функция распределения
случайной величины
– случайная величина с некоторой
функцией распределения, которой
соответствует функция распределения
случайной величины
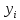
Спецификация модели – формулировка вида модели исходя из соответствующей теории связи между переменными.
Основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели:
В парной регрессии спецификация модели связана с выбором вида математической функции, а в множественной – также с отбором факторов, включаемых в модель.
В
парной регресcии
выбор вида математической функции
 может быть осуществлен тремя методами:
может быть осуществлен тремя методами:
– графическим (базируется на поле корреляции);
– аналитическим, т.е. исходя из теории изучаемой взаимосвязи;
– экспериментальным (путем сравнения величины остаточной дисперсии Dост, рассчитанной при разных моделях).
Результаты многих исследований подтверждают, что число наблюдений должно в 6-7 раз превышать число рассчитываемых параметров при переменной х.
1.2 Метод наименьших квадратов
Построение линейной регрессии сводится к оценке её параметров – a и b .
Одним из методов оценки параметров линейной регрессии является метод наименьших квадратов.
Метод
наименьших квадратов позволяет получить
такие оценки параметров а и b,
при которых сумма квадратов отклонений
фактических значений результативного
признака у от расчетных (теоретических)
 минимальна:
минимальна:

Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной:

Следовательно,

Т.е.
задача наилучшей аппроксимации набора
наблюдений
 линейной функцией
линейной функцией
 сводится к минимизации функционала
сводится к минимизации функционала
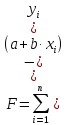
Запишем
необходимые условия экстремума функции
двух переменных
 ,
т.е. приравняем к нулю её частные
производные:
,
т.е. приравняем к нулю её частные
производные:

или

Раскроем скобки и получим систему нормальных уравнений для оценки параметров а и b:

Решение a и b системы можно легко найти:


где 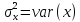 – выборочная дисперсия
переменной х;
– выборочная дисперсия
переменной х;
cov(x,y) – выборочный корреляционный момент или выборочная ковариация
Замечание:
1)
Уравнение прямой линии
 ,
полученное в результате минимизации
функционала F
проходит через точку
,
полученное в результате минимизации
функционала F
проходит через точку
 .
.
2)
Подставляя полученное значение а
из первого уравнения системы ( ) в
уравнение регрессии
 получим
получим

или

где параметр b называется коэффициентом регрессии у по х. Его величина показывает на сколько единиц в среднем изменяется переменная у при увеличении переменной х на одну единицу.
1.3 Уравнения в отклонениях
Обозначим
через
 и
и
 отклонения от средних по выборке значений
отклонения от средних по выборке значений
 и
и
 ,
,
 ,
,
 .
.
Решим ту же задачу:
Подобрать
линейную функцию
 минимизирующую функционал
минимизирующую функционал

Из
геометрических соображений ясно, что
решением задачи будет та же прямая на
плоскости (x,y),
что и для исходных данных
 .
Переход от х,у
к отклонениям хʹ,уʹ
означает
лишь перенос начала координат в точку
.
Переход от х,у
к отклонениям хʹ,уʹ
означает
лишь перенос начала координат в точку

Решая задачу, мы получим


и
уравнение регрессии в отклонениях
примет вид

1.4 Парное уравнение регрессии может быть записано в матричной форме:

где Y
– вектор-столбец размерности ( фактических значений результативного
признака;
фактических значений результативного
признака;
B
– вектор-столбец
размерности ( подлежащих оценке параметров модели,
т.е. коэффициента регрессии b
и свободного члена (параметра а
в уравнении
подлежащих оценке параметров модели,
т.е. коэффициента регрессии b
и свободного члена (параметра а
в уравнении
 );
);
X=(x0,x1)
– матрица размерности ( значений факторов. При этом х0=1
и связано с наличием в уравнении регрессии
свободного члена, а х1 –
собственно реальные значения включенного
в уравнение регрессии фактора;
значений факторов. При этом х0=1
и связано с наличием в уравнении регрессии
свободного члена, а х1 –
собственно реальные значения включенного
в уравнение регрессии фактора;
Е
– вектор-столбец случайной величины
 размерности .
размерности .
Матрица исходных данных примет вид:




Оценка вектора В после применения МНК в матричной форме составит:

1.5 Основные гипотезы, лежащие в основе классической линейной модели парной регрессии
1. Спецификация модели

2.
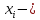 детерминированная величина
детерминированная величина
Вектор
 не коллинеарен вектору
не коллинеарен вектору

3.
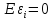 , т.е. математическое ожидание ошибок
(остатков) равно нулю.
, т.е. математическое ожидание ошибок
(остатков) равно нулю.
4.
 неизменность дисперсий ошибок (остатков),
дисперсия не зависит от i.
неизменность дисперсий ошибок (остатков),
дисперсия не зависит от i.
5.
 некоррелированность ошибок для разных
наблюдений
некоррелированность ошибок для разных
наблюдений
6.
Ошибки
 имеют совместное нормальное распределение
имеют совместное нормальное распределение
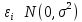
Комментарии к основным гипотезам:
Спецификация
модели отражает наше представление о
механизме зависимости
 от
от
 и сам выбор объясняющей переменной
и сам выбор объясняющей переменной
 .
.
Условие
 означает, что
означает, что
 ,
т.е. при фиксированном
,
т.е. при фиксированном
 среднее ожидаемое значение
среднее ожидаемое значение
 равно a+bxi.
равно a+bxi.
Условие
независимости дисперсии ошибки от
номера наблюдения (от регрессора
 )
:
)
:
 ,
i=1,…,n
называется гомоскедастичностью.
,
i=1,…,n
называется гомоскедастичностью.
Случай,
когда условие гомоскедастичности не
выполняется называется гетероскедастичностью.
Условие
 указывает на некоррелированность
ошибок для разных наблюдений. Это условие
часто нарушается в случае, когда наши
данные являются временными рядами.
указывает на некоррелированность
ошибок для разных наблюдений. Это условие
часто нарушается в случае, когда наши
данные являются временными рядами.
В случае, когда это условие не выполняется, говорят об автокорреляции ошибок.
