
- •Тема 1. Природа эконометрики
- •1.1. Общие понятия эконометрических моделей
- •1. 2. Типы эконометрических моделей
- •1. 3. Типы данных
- •Тема 2. Корреляционный анализ в эконометрических исследованиях
- •2.1. Функциональная, статистическая и корреляционная зависимости
- •2.2. Понятие о двумерном корреляционном анализе
- •2.3. Понятие о многомерном корреляционном анализе
- •2.4. Ранговая корреляция
- •Тема 3. Регрессионный анализ в эконометрических исследованиях
- •3.1. Задача регрессионного анализа
- •3.2. Идентификация модели регрессии
- •3.3. Линейная парная регрессия и оценка параметров
- •3.4. Проверка значимости параметров линейной парной регрессии
- •3.5. Интервалы прогноза по линейному уравнению регрессии
- •3.6. Нелинейная регрессия
- •3.7. Корреляционное отношение и индекс корреляции
- •3.8. Множественный регрессионный анализ
- •4.9. Ковариационная матрица и ее выборочная оценка
- •4.10. Определение доверительных интервалов для коэффициентов и функции множественной регрессии
- •4.11. Мультиколлинеарность
- •Тема 5. Методы и модели анализа динамики экономических процессов
- •5.1. Понятия экономических рядов динамики
- •5.2. Предварительный анализ динамических рядов экономических показателей
- •5.3. Сглаживание динамических рядов
- •4.3. Расчет показателей динамики развития эконометрических процессов
- •4.4. Тренд-сезонные экономические процессы и их анализ
- •Тема 5. Модели прогнозирования экономических процессов
- •5.7. Трендовые модели на основе кривых роста
- •5.2. Оценка адекватности и точности трендовых моделей
- •5.3. Прогнозирование экономической динамики на основе трендовых моделей
- •5.4. Адаптивные модели прогнозирования
- •Лучшая модель ар(1,1)
- •Характеристика остатков
- •Тема 8. Системы взаимозависимых эконометрических моделей
- •8.1. Особенности систем взаимозависимьех моделей
- •8.2. Формы представления систем взаимозависимых эконометрических моделей
- •8.3. Косвенный метод оценки коэффициентов структурной формы систем взаимозависимых эконометрических моделей
- •8.4. Оценивание параметров структурной формы на основе двухшагового мнк с использованием инструментальных переменных
- •1. На первом шаге конструируются новые значения зависимых
- •2. На втором шаге значения используются вместо значений
- •8.5. Оценки параметров системы взаимозависимых эконометрических моделей с использованием трехшагового мнк
4.9. Ковариационная матрица и ее выборочная оценка
Вариации оценок параметров будут, в конечном счете, определять точность уравнения множественной регрессии. Для их измерения в многомерном регрессионном анализе рассматривают так называемую ковариационную матрицу К, являющуюся матричным аналогом дисперсии одной переменной:
 .
.
где
элементы
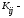 ковариации
(или
корреляционные
моменты) оценок
параметров
ковариации
(или
корреляционные
моменты) оценок
параметров
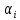 и
и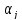
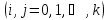 .
Ковариация
двух переменных определяется как
математическое ожидание произведения
отклонений этих переменных от их
математических ожиданий [Ссылка]. Поэтому
.
Ковариация
двух переменных определяется как
математическое ожидание произведения
отклонений этих переменных от их
математических ожиданий [Ссылка]. Поэтому
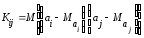 , (13.28)
, (13.28)
где
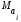 и
и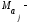 математические
ожидания соответственно для параметров
математические
ожидания соответственно для параметров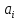 и
и
 .
.
Ковариация характеризует как степень рассеяния значений двух переменных относительно их математических ожиданий, так и взаимосвязь этих переменных.
В
силу того, что оценки
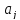 ,
полученные методом наименьших квадратов,
являются несмещенными оценками параметров
,
полученные методом наименьших квадратов,
являются несмещенными оценками параметров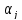 ,
т.е.
,
т.е.
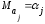 ,
выражение(13.28)
примет
вид:
,
выражение(13.28)
примет
вид:
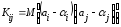 .
.
Рассматривая ковариационную матрицу К, легко заметить, что на ее главной диагонали находятся дисперсии опенок параметров регрессии, ибо
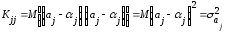 .
(13.29)
.
(13.29)
В сокращенном виде ковариационная матрица К имеет вид:
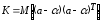 .
(13.30)
.
(13.30)
Учитывая (13.28) мы можем записать
 .
.
Тогда выражение (12.30) примет вид:
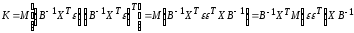 ,
(13.31)
,
(13.31)
ибо элементы матрицы X —неслучайные величины.
Матрица
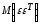 представляет
собой ковариационную матрицу
вектора возмущений
представляет
собой ковариационную матрицу
вектора возмущений
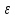 :
:
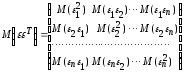
в
которой все элементы, не лежащие на
главной диагонали, равны нулю в силу
предпосылки 4
о
некоррелированности возмущений
 ,
и
,
и между
собой,
а
все элементы, лежащие на главной
диагонали, в силу предпосылок 2
и
3
регрессионного
анализа
равны
одной и той же дисперсии
между
собой,
а
все элементы, лежащие на главной
диагонали, в силу предпосылок 2
и
3
регрессионного
анализа
равны
одной и той же дисперсии
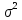 :
:
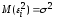 .
.
Поэтому
матрица
 ,
где
,
где
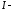 единичная
матрица
единичная
матрица
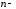 го
го
порядка.
Следовательно, в силу (13.31)
ковариационная
матрица вектора
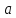 оценок
параметров:
оценок
параметров:
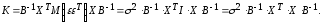
Так
как
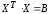 и
и
 ,
то окончательно получим:
,
то окончательно получим:
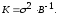 (13.32)
(13.32)
Таким
образом, с
помощью обратной матрицы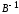 нормальных
уравнении регрессии
определяется
не только сам вектор
нормальных
уравнении регрессии
определяется
не только сам вектор
 оценок
параметров (13.28),
но
и дисперсии и ковариации его компонент.
оценок
параметров (13.28),
но
и дисперсии и ковариации его компонент.
Входящая в (13.32) дисперсия возмущений неизвестна. Заменив ее выборочной остаточной дисперсией
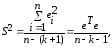 (13.33)
(13.33)
по
(13.32)
получаем
выборочную оценку ковариационной
матрицы К.
(В
знаменателе выражения (13.33)
стоит
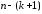 ,
а
не
,
а
не
 ,
как
это было выше в (13.6).
Это
связано с тем, что теперь
,
как
это было выше в (13.6).
Это
связано с тем, что теперь
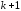 степеней
свободы (а не две) теряются при определении
неизвестных параметров, число которых
вместе со свободным членом
степеней
свободы (а не две) теряются при определении
неизвестных параметров, число которых
вместе со свободным членом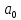 равно
равно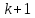 .
.
4.10. Определение доверительных интервалов для коэффициентов и функции множественной регрессии
Перейдем
теперь к оценке значимости коэффициентов
регрессии
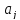 и
построению доверительного интервала
для параметров регрессионной модели
и
построению доверительного интервала
для параметров регрессионной модели
 .
.
В
силу (13.29),
(13.32) и
изложенного выше оценка дисперсии
коэффициента регрессии
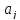 определится
по формуле:
определится
по формуле:
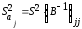
где
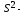 несмещенная
оценка параметра
несмещенная
оценка параметра
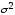 ;
;
 диагональный
элемент матрицы
диагональный
элемент матрицы
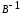 .
.
Среднее
квадратическое отклонение (стандартная
ошибка) коэффициента регрессии
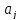 примет
вид:
примет
вид:
 .
(13.34)
.
(13.34)
Значимость
коэффициента регрессии
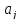 можно
проверить, если учесть, что статистика
можно
проверить, если учесть, что статистика
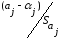 имеет
имеет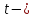 распределение
Стьюдента с
распределение
Стьюдента с
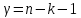 степенями
свободы. Поэтому
степенями
свободы. Поэтому
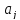 значимо
отличается от нуля на уровне
значимости
значимо
отличается от нуля на уровне
значимости
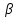 ,
если
,
если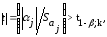 соответствующий
соответствующий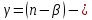 ныйдоверительный
интервал для параметра
ныйдоверительный
интервал для параметра
 есть
есть
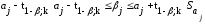 .
(13.35)
.
(13.35)
Наряду
с интервальным оцениванием коэффициентов
регрессии по (13.35)
весьма
важным для оценки точности определения
зависимой переменной (прогноза) является
построение доверительного
интервала для функции регрессии или
для условного математического
ожидания зависимой переменной
 ,
найденного в предположении, что
объясняющие переменные
,
найденного в предположении, что
объясняющие переменные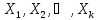 приняли
значения, задаваемые вектором
приняли
значения, задаваемые вектором
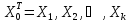 .Выше
такой интервал получен для уравнения
парной регрессии (см. (13.13)
и
(13.12)).
Обобщая
соответствующие выражения на случай
множественной регрессии, можно получить
доверительный интервал для
.Выше
такой интервал получен для уравнения
парной регрессии (см. (13.13)
и
(13.12)).
Обобщая
соответствующие выражения на случай
множественной регрессии, можно получить
доверительный интервал для
 :
:

где
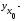 групповая
средняя, определяемая по уравнению
регрессии,
групповая
средняя, определяемая по уравнению
регрессии,
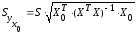 (13.36)
(13.36)
— ее стандартная ошибка.
При
обобщении формул (13.15)
и
(13.14)
аналогичный
доверительный
интервал для индивидуальных значений
зависимой переменной
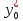 примет
вид:
примет
вид:
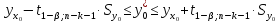 (13.37)
(13.37)
где
 .
(13.38)
.
(13.38)
Доверительный
интервал для дисперсии возмущений
 в
множественной регрессии с надежностью
в
множественной регрессии с надежностью
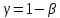 строится аналогично парной модели
по формуле(13.20)
с
соответствующим изменением числа
степеней свободы критерия
строится аналогично парной модели
по формуле(13.20)
с
соответствующим изменением числа
степеней свободы критерия
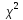 :
:
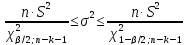 (13.39)
(13.39)
Пример
13.6.
По
данным примера 13.4
оценить
сменную добычу
угля на одного рабочего для шахт с
мощностью пласта 8 м и уровнем механизации
работ 6%; найти 95%-ные доверительные
интервалы для индивидуального и среднего
значений сменной добычи угля на 1
рабочего для таких же шахт. Проверить
значимость коэффициентов регрессии и
построить для них 95%-ные доверительные
интервалы. Найти с надежностью 0,95
интервальную оценку для дисперсии
возмущений
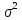 .
.
Решение. В примере 13.4 уравнение регрессии получено в виде:
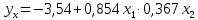 .
По
условию надо оценить
.
По
условию надо оценить
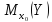 ,
где
,
где
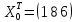 .
Выборочной оценкой
.
Выборочной оценкой ,
является
групповая средняя, которую найдем по
уравнению регрессии:
,
является
групповая средняя, которую найдем по
уравнению регрессии:
 .
Для построения доверительного
интервала для М (у) необходимо знать
дисперсию его оценки
.
Для построения доверительного
интервала для М (у) необходимо знать
дисперсию его оценки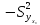 .
Для
ее вычисления обратимся к табл. 13.7
(точнее к ее двум последним столбцам,
при составлении которых учтено, что
групповые средние определяются по
полученному уравнению регрессии).
.
Для
ее вычисления обратимся к табл. 13.7
(точнее к ее двум последним столбцам,
при составлении которых учтено, что
групповые средние определяются по
полученному уравнению регрессии).
Теперь
по (13.37):
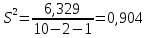 и
и
 (т).
(т).
Определяем стандартную ошибку групповой средней г> по формуле (13.41). Вначале найдем
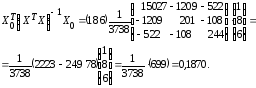
Теперь
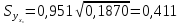 (т).
(т).
По
табл. IV приложений при числе степеней
свободы
 находим
находим
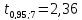 .
По
(13.40)
доверительный
интервал для
.
По
(13.40)
доверительный
интервал для
 ,
равен
,
равен
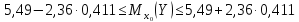 или
или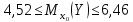 (т).
(т).
Итак, с надежностью 0,95 средняя сменная добыча угля на одного рабочего для шахт с мощностью пласта 8 м и уровнем механизации работ 6% находится в пределах от 4,52 до 6,46 т.
Сравнивая
новый доверительный интервал для функции
регрессии
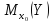 ,
полученный
с учетом двух объясняющих переменных,
с аналогичным интервалом с учетом одной
объясняющей переменной (см. пример
13.1),
можно
заметить уменьшение его величины. Это
связано с тем, что включение в модель
новой объясняющей переменной позволяет
несколько повысить точность модели
за счет увеличения взаимосвязи зависимой
и объясняющей переменных (см. ниже).
,
полученный
с учетом двух объясняющих переменных,
с аналогичным интервалом с учетом одной
объясняющей переменной (см. пример
13.1),
можно
заметить уменьшение его величины. Это
связано с тем, что включение в модель
новой объясняющей переменной позволяет
несколько повысить точность модели
за счет увеличения взаимосвязи зависимой
и объясняющей переменных (см. ниже).
Найдем
доверительный интервал для индивидуального
значения
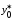 при
при
 по
(13.43):
по
(13.43):
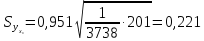 (т)
и по (13.42):
(т)
и по (13.42):
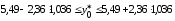 ,
т. е.
,
т. е.
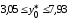 (т).
(т).
Итак, с надежностью 0,95 индивидуальное значение сменной добычи угля в шахтах с мощностью пласта 8 м и уровнем механизации работ 6% находится в пределах от 3,05 до 7,93 (т).
Проверим
значимость коэффициентов регрессии
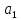 и
и
 .
В
примере 13.4
получены
.
В
примере 13.4
получены
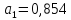 и
и
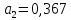 .
Стандартная
ошибка
.
Стандартная
ошибка
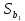 в
соответствии с (13.38)
равна:
в
соответствии с (13.38)
равна:
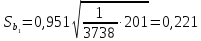 .
Так
как
.
Так
как
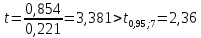 ,
то
коэффициент
,
то
коэффициент
 значим.
Аналогично вычисляем
значим.
Аналогично вычисляем
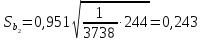 и
и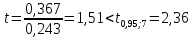 т.е. коэффициент
т.е. коэффициент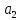 незначим
на 5%-ном уровне.
незначим
на 5%-ном уровне.
Доверительный
интервал имеет смысл построить только
для значимого коэффициента регрессии
 :
по
(13.39)
:
по
(13.39)
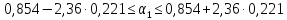 или
или
 .
.
Итак,
с надежностью 0,95 за счет изменения на
1 м мощности пласта
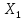 (при
неизменном
(при
неизменном
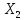 )
сменная
добыча угля на одного рабочего У
будет изменяться в пределах от 0,332 до
1,376 т.
)
сменная
добыча угля на одного рабочего У
будет изменяться в пределах от 0,332 до
1,376 т.
Найдем
95%-ный доверительный интервал для
параметра ст2.
Учитывая, что
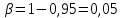 ,
,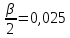 ,
, найдем по табл.
V
приложений при
найдем по табл.
V
приложений при
 степенях свободы
степенях свободы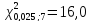 ;
;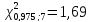 и по формуле(13.43')
и по формуле(13.43')

Таким образом, с надежностью 0,95 дисперсия возмущений заключена в пределах от 0,565 до 5,35, а их стандартное отклонение — от 0,751 до 2,31 (т).
Формально переменные, имеющие незначимые коэффициенты регрессии, могут быть исключены из рассмотрения. В экономических исследованиях исключению переменных из регрессии должен предшествовать тщательный качественный анализ. Поэтому может оказаться целесообразным все же оставить в регрессионной модели одну или несколько объясняющих переменных, не оказывающих существенного (значимого) влияния на зависимую переменную.
