
MetodTM2
.pdf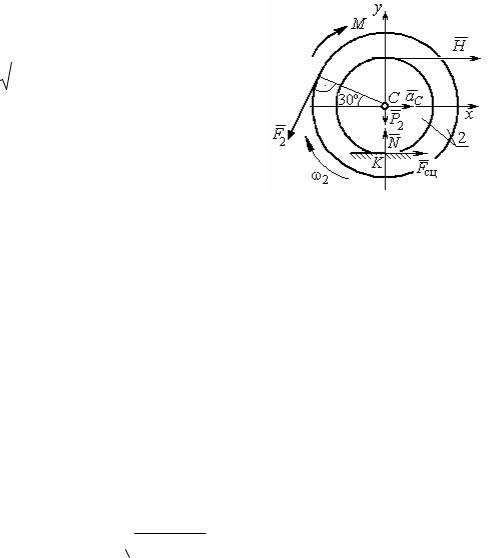
Для определения динамической реакции шарнира О1 диска 1 применим теорему о движении центра масс. Выберем оси координат O1x и O1y , как показано на рис. 5.9, и составим уравнение движения центра масс диска 1 в
проекциях на оси координат с учётом того, что сам центр масс неподвижен и его ускорение равно нулю.
Получим систему:
|
H + X1 − F1sin45o = 0, |
Y1 − P1 − F1cos45o = 0 . |
|||||
Отсюда, с учётом найденной величины усилия в стержне Н = 28,63 Н, на- |
|||||||
ходим составляющие |
динамической |
реакции |
|
||||
шарнира: X1 = 27,94 H, Y1 = 96,57 H. Полная реак- |
|
||||||
|
= |
|
|
=100,53 Н. |
|
|
|
ция шарнира R |
X 2 |
+ Y 2 |
|
|
|||
O |
1 |
1 |
|
|
|
||
1 |
|
|
|
|
|
|
|
Для определения величины силы сцепления |
|
||||||
диска 2 с поверхностью качения и нормальной |
|
||||||
составляющей реакции опоры диска используем |
|
||||||
теорему о движении центра масс. Силы, прило- |
Рис. 5.10. Силы, действующие |
||||||
на диск 2 во время движения |
|||||||
женные к диску 2, и выбранная система коорди- |
|||||||
|
|||||||
нат хСу показаны на рис. 5.10. Уравнения движения центра масс диска 2 в про-
екциях на оси x, y имеют вид:
m2aC = H + Fсц − F2cos60o ,
0 = −F2cos30o − P2 + N .
С учетом найденных значений реакции стержня Н = 28,63 Н и ускорения центра масс диска 2 aC = 6,85 м/с2, находим силу сцепления и нормальную ре-
акцию опоры: Fсц = 28,27 Н, N = 85,98 Н.
Полная реакция опоры RK = 
 N 2 + Fсц2 = 90,51 Н.
N 2 + Fсц2 = 90,51 Н.
123
6.АНАЛИТИЧЕСКАЯ МЕХАНИКА
6.1.Принципы механики. Общее уравнение динамики
Силой инерции материальной точки называют векторную величину, мо-
дуль которой равен произведению массы точки на модуль её ускорения, и на-
правленную противоположно этому ускорению
|
r |
|
Rи = −ma , где m – масса точки; a – вектор ус- |
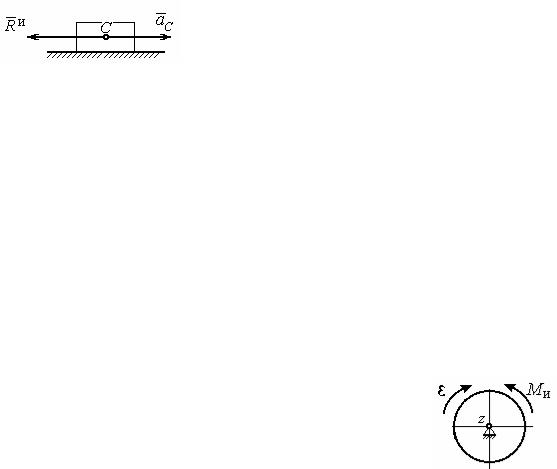
Рис. 6.1. Главный вектор сил |
корения точки. |
|
|
инерции при поступательном |
При поступательном движении тела с ус- |
движении твердого тела |
корением центра масс aс система сил инерции, |
|
приложенных к каждой точке тела, приводится к главному вектору сил инер-
ции Rи , равному по величине Rи = maс , приложенному в центре масс тела и направленному в сторону, противоположную ускорению aс (рис. 6.1).
При вращении тела вокруг неподвижной оси z, проходящей через центр масс, главный вектор сил инерции, приведённый к центру масс тела, обращает-
ся в нуль (так как ускорение центра масс равно нулю). Таким образом, система
сил инерции приводится к паре сил с моментом |
|
|
M и , равным главному моменту сил инерции отно- |
|
|
сительно оси вращения. Величина главного мо- |
|
|
мента сил инерции M и = J zε, где |
J z – момент |
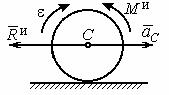
Рис. 6.2. Главный момент |
|
|
сил инерции при враще- |
инерции тела относительно оси z; ε |
– угловое ус- |
нии тела вокруг оси, про- |
корение тела. Направлен главный |
момент сил |
ходящей через центр масс |
|
||
инерции в сторону, противоположную угловому ускорению (рис. 6.2).
При плоскопараллельном движении тела с ускорением центра масс aс и
угловым ускорением ε система сил инерции, приложенных к каждой точке те-
ла, приводится к силе Rи , равной главному вектору сил инерции, и паре сил с моментом M и , равным главному моменту сил инерции относительно оси,
124
проходящей через центр масс тела перпендикулярно плоскости движения
(рис. 6.3). Главный вектор сил инерции равен по модулю произведению массы |
||
тела на ускорение его центра масс: Rи = ma , при- |
|
|
с |
|
|
ложен в центре масс тела и направлен в сторону, |
|
|
противоположную ускорению aс центра масс. |
|
|
Главный момент сил инерции равен по величине |
Рис. 6.3. Главный вектор |
|
произведению момента инерции тела относительно |
и главный момент сил |
|
инерции при плоскопа- |
||
|
||
оси, проходящей через центр масс перпендикуляр- |
раллельном движении |
|
но плоскости движения, на угловое ускорение тела: |
твердого тела |
|
|
||
M и = Jсε , где Jс – момент инерции тела. Направлен главный момент сил инерции в сторону, противоположную угловому ускорению (см. рис. 6.3).
Принцип Даламбера для системы. Если в любой момент времени к ка-
ждой из точек системы кроме действующих на нее внешних и внутренних сил присоединить соответствующие силы инерции, то полученная система сил бу-
дет уравновешенной. Принцип Даламбера даёт возможность составлять уравне-
ния движения механической системы в виде уравнений равновесия:
|
|
|
åF e + Rи = 0, åM |
O |
(F e ) + M и = 0, |
||
|
|
|
k |
|
k |
O |
|
где F e – |
внешние силы, приложенные к системе; |
Rи – главный вектор сил |
|||||
k |
|
|
|
|
|
|
|
инерции; |
M |
О |
(F e ) – момент внешних сил, приложенных к системе, относитель- |
||||
|
|
k |
|
|
|
|
|
но произвольного центра О; MOи |
– главный момент сил инерции относительно |
||||||
центра О. |
|
|
|
|
|
|
|
Силы, действующие на систему, можно подразделить на активные и ре-
акции связей. Идеальными связями в механической системе называют такие связи, для которых сумма элементарных работ их реакций на любом возмож-
ном перемещении равна нулю.
Принцип возможных перемещений. Для равновесия механической сис-
темы с идеальными связями необходимо и достаточно, чтобы сумма
125
элементарных работ всех активных сил, приложенных к точкам системы, была равна нулю на любом возможном перемещении системы: åδA(Fkакт ) = 0, где
δA(Fkакт ) – элементарная работа активных сил на возможном перемещении.
Совместное применение принципа Даламбера и принципа возможных пе-
ремещений приводит к формулировке общего уравнения динамики.
Общее уравнение динамики. При движении механической системы с идеальными связями в каждый момент времени сумма элементарных работ всех приложенных активных сил и сил инерции на любом возможном перемещении равна нулю: å δA(Fkакт ) + åδA(Rkи ) = 0, где δA(Fkакт ) , δA(Rkи ) – элементарные работы активных сил и сил инерции, приложенных к системе, на её воз-
можном перемещении.
При вычислении элементарных работ активных сил и сил инерции ис-
пользуют обычные формулы для вычисления работы сил на элементарном пе-
ремещении точек их приложения. При этом переменные силы на элементарном перемещении точек их приложения считаются постоянными.
6.2.Задание Д6. Исследование механической системы
сприменением общего уравнения динамики
Механическая система состоит из груза и двух дисков. Радиус однородно-
го диска R или r и радиусы ступеней ступенчатого диска R и r указаны на схеме.
Тела соединены нерастяжимыми нитями или невесомыми стержнями. Система движется в вертикальной плоскости из состояния покоя под действием сил тя-
жести P1, P2 , P3 , постоянной силы F , а также пары сил с переменным момен-
том М. Направление действия силы F и наклон плоскости движущихся тел оп-
ределяются углами α и β , показанными на схемах. Радиус инерции ступенча-
того диска относительно оси, проходящей через центр масс перпендикулярно плоскости движения, iz .
126
Качение дисков без проскальзывания. Скольжение между невесомым стержнем и дисками отсутствует. Движение грузов по плоскости без трения.
Нити и стержни, соединяющие груз и диски, параллельны соответствующим плоскостям, по которым двигаются тела.
Найти уравнение движения центра масс диска 3. Определить реакцию шарнира диска 2 в момент времени t = 1 с. Варианты задания приведены на рис. 6.4 – 6.5. Исходные данные выбираются из табл. 6.1.
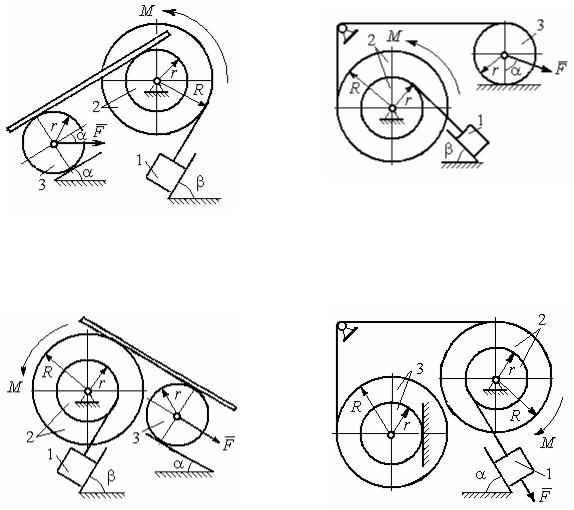
Варианты № 1, 11, 21 |
Варианты № 2, 12, 22 |
|
|
|
|
Варианты 3, 13, 23 |
Варианты № 4, 14, 24 |
|
|
|
|
Рис. 6.4. Задание Д6. Исследование движения механической системы с применением общего уравнения динамики.
Номера вариантов задания 1 – 4, 11 – 14, 21 – 24
127

|
Окончание вариантов задания Д6 |
Варианты № 5, 15, 25 |
Варианты № 6, 16, 26 |
|
|
|
|
|
|
Варианты № 7, 17, 27 |
Варианты № 8, 18, 28 |
|
|
|
|
|
|
Варианты № 9, 19, 29 |
Варианты № 10, 20, 30 |
|
|
|
|
Рис. 6.5. Задание Д6. Исследование движения механической системы с применением общего уравнения динамики.
Номера вариантов задания 5 – 10, 15 – 20, 25 – 30
128
Таблица 6.1
Исходные данные задания Д6. Исследование движения механической системы с применением общего уравнения динамики
Номер |
Р1, Н |
Р2, Н |
Р3, Н |
F, Н |
М, Н·м |
α , |
β , |
R, |
r, |
iz, м |
варианта |
||||||||||
задания |
|
|
|
|
|
град |
град |
м |
м |
|
1 |
10 |
20 |
8 |
20 |
3(2+t2) |
30 |
60 |
0,6 |
0,3 |
0,4 |
2 |
10 |
22 |
15 |
15 |
4(t+3) |
30 |
30 |
0,8 |
0,4 |
0,6 |
3 |
5 |
18 |
10 |
6 |
8(t2+1) |
90 |
30 |
0,4 |
0,3 |
0,3 |
4 |
5 |
22 |
10 |
5 |
14(t2+t+1) |
30 |
– |
0,6 |
0,5 |
0,6 |
5 |
5 |
20 |
16 |
9 |
3(t2+4) |
45 |
60 |
0,6 |
0,3 |
0,5 |
6 |
10 |
16 |
14 |
15 |
4(5+t) |
60 |
30 |
1,0 |
0,6 |
0,8 |
7 |
6 |
20 |
20 |
8 |
9(3t2+2) |
45 |
– |
0,8 |
0,6 |
0,8 |
8 |
16 |
25 |
15 |
12 |
5(t2+4) |
30 |
60 |
1,2 |
0,6 |
0,8 |
9 |
5 |
20 |
12 |
8 |
4(3+5t) |
60 |
30 |
0,6 |
0,4 |
0,5 |
10 |
6 |
25 |
8 |
10 |
5(3t+6) |
30 |
– |
1,0 |
0,8 |
0,9 |
11 |
4 |
22 |
8 |
15 |
2+ t2 |
45 |
45 |
0,8 |
0,4 |
0,6 |
12 |
15 |
18 |
15 |
10 |
5(t+3) |
30 |
60 |
1,0 |
0,5 |
0,7 |
13 |
6 |
20 |
10 |
4 |
5(t2+2) |
30 |
60 |
0,6 |
0,5 |
0,4 |
14 |
10 |
25 |
15 |
8 |
16(t+2) |
60 |
– |
0,8 |
0,6 |
0,7 |
15 |
8 |
18 |
20 |
10 |
6(t+2) |
30 |
90 |
1,2 |
0,6 |
1,0 |
16 |
8 |
18 |
12 |
12 |
5(3+t2) |
90 |
60 |
0,8 |
0,6 |
0,7 |
17 |
5 |
20 |
10 |
10 |
2t2+20 |
60 |
– |
0,9 |
0,6 |
0,8 |
18 |
20 |
15 |
20 |
15 |
3(t+4) |
60 |
30 |
0,8 |
0,4 |
0,7 |
19 |
8 |
20 |
12 |
10 |
4(3+t) |
45 |
45 |
1,2 |
0,4 |
0,8 |
20 |
12 |
20 |
10 |
6 |
6(3t+4) |
45 |
– |
1,0 |
0,6 |
0,9 |
21 |
15 |
25 |
12 |
12 |
6+t2 |
60 |
60 |
0,6 |
0,3 |
0,5 |
22 |
20 |
22 |
18 |
15 |
2(2t+9) |
45 |
45 |
0,8 |
0,4 |
0,6 |
23 |
8 |
24 |
12 |
8 |
7(3t2+2) |
30 |
45 |
0,8 |
0,5 |
0,6 |
24 |
12 |
20 |
18 |
10 |
6(t+4) |
90 |
– |
0,5 |
0,3 |
0,4 |
25 |
5 |
20 |
12 |
12 |
9(2+t2) |
60 |
30 |
1,4 |
0,7 |
1,2 |
26 |
10 |
12 |
10 |
8 |
6(2+t) |
30 |
45 |
1,2 |
0,8 |
0,9 |
27 |
6 |
18 |
16 |
14 |
8(2t2+3) |
30 |
– |
0,8 |
0,2 |
0,6 |
28 |
10 |
20 |
20 |
20 |
3(t2+3) |
45 |
30 |
0,6 |
0,3 |
0,5 |
29 |
10 |
18 |
8 |
12 |
5(4+t+ t2) |
30 |
60 |
1,2 |
0,8 |
0,9 |
30 |
8 |
18 |
10 |
15 |
8(t2+5) |
60 |
– |
1,0 |
0,8 |
0,9 |
Пример выполнения задания Д6. Исследование движения механической системы с применением общего уравнения динамики
Механическая система состоит из груза 1, движущегося поступательно,
ступенчатого диска 2 (каток), катящегося по неподвижной поверхности,
129
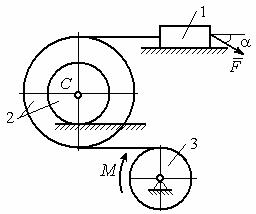
и однородного диска 3 (блок), вращающегося вокруг неподвижной оси, прохо-
дящей через центр масс блока (рис. 6.6). Качение катка 2 без проскальзывания,
|
скольжение груза 1 – без трения. |
||||
|
Движение системы |
происходит |
под |
||
|
действием сил тяжести, силы F , |
при- |
|||
|
ложенной к грузу 1 и пары сил |
с мо- |
|||
|
ментом |
М, приложенной к диску 3. |
|||
|
Найти |
уравнение |
движения |
центра |
|
|
масс катка 2, если движение системы |
||||
Рис. 6.6. Схема движения механической |
началось из состояния покоя. Опреде- |
||||
системы |
лить реакцию шарнира диска |
3 |
как |
||
|
|||||
функцию времени и в момент t = 1 с, если: P1 = 10 Н; P2 = 20 Н; P3 = 15 Н;
F = 5(t+1) Н; M = 6(1+ 2t) Н·м; R2 = 0,8 м; r2 = 0,2 м; R3 = 0,4 м; i2С = 0,6 м.
Решение
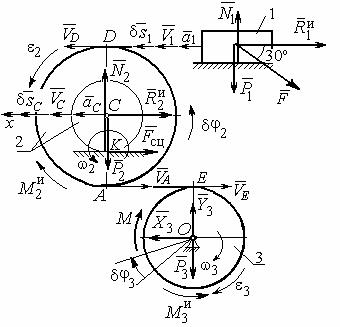
В рассматриваемой механической системе активными силами являются силы тяжести P1, P2 , P3 , сила F и пара сил с моментом М. Реакциями связей являются нормальные реакции опор: N1, N2 , сила сцепления катка 2 с непод-
вижной поверхностью Fсц и реакция шарнира О блока 3, разложенная на со-
ставляющие X3 , Y3 (рис. 6.7). Связи идеальные, так как скольжение груза 1
происходит по гладкой поверхности без трения, качение диска 2 без проскаль-
зывания, а ось вращения блока 3 неподвижна. Предположим, направление дви-
жения в системе задаёт пара сил с моментом М, приложенная к блоку 3. Блок 3
вращается с угловой скоростью ω3 и угловым ускорением ε3 , скорость центра масс катка 2 – VC , его ускорение – aC , угловые скорость и ускорение катка 2 –
ω2 и ε2 , скорость и ускорение груза 1 – V1 и a1 . Направления векторов скоро-
стей и ускорений точек и угловых скоростей и ускорений тел показаны на рис. 6.7.
130
Общее уравнение динамики имеет вид:
|
|
åδA(F акт ) + åδA(Rи ) = 0 . |
|||
|
|
|
k |
k |
|
Присоединим к телам системы силы инерции. Груз 1 движется поступа- |
|||||
тельно. Главный вектор сил |
|
|
|||
инерции груза 1 |
Rи приложен |
|
|
||
|
1 |
|
|
|
|
в центре масс груза и направ- |
|
|
|||
лен в сторону, противополож- |
|
|
|||
ную ускорению a1 груза 1. |
|
|
|||
Модуль главного вектора сил |
|
|
|||
инерции груза 1 Rи = m1a1, где |
|
|
|||
|
1 |
|
|
|
|
m1 – масса груза 1; a1 – вели- |
|
|
|||
чина ускорения груза 1. |
|
|
|
||
Выберем |
центром |
при- |
Рис. 6.7. Расчётная схема исследования движения |
||
ведения сил инерции катка 2, |
|||||
|
механической системы |
||||
|
|
|
|
||
совершающего |
плоское |
дви- |
|
|
|
жение, его центр масс – точку С. Тогда система сил инерции катка 2 приводятся к силе, равной главному вектору сил инерции R2и , приложенному в центре масс катка 2, и паре сил с моментом, равным главному моменту сил инерции M2и от-
носительно оси, проходящей через центр масс перпендикулярно плоскости движения. Главный вектор сил инерции направлен в сторону, противополож-
ную ускорению aC , и равен по величине R2и = m2 aС , где m2 – масса катка 2; aC
– величина ускорения центра масс, Главный момент сил инерции по величине равен: M 2и = J2Cε2 , где J2C – момент инерции катка 2 относительно оси, про-
ходящей через центр масс перпендикулярно плоскости движения; ε2 – угловое ускорение катка 2. Направление главного момента сил инерции M 2и в сторону,
противоположную угловому ускорению ε2.
131
Главный вектор сил инерции, приложенных к блоку 3 и приведённых к центру масс блока, равен нулю, так как блок вращается вокруг неподвижной оси, проходящей через центр масс, и ускорение центра масс блока равно нулю.
Силы инерции блока 3 приводятся к паре сил, момент которой равен главному
моменту сил инерции M3и относительно оси вращения. Главный момент сил инерции блока 3 равен по величине M3и = J3Oε3 , где J3O – момент инерции блока 3 относительно оси вращения; ε3 – угловое ускорение блока 3, и направ-
лен в сторону, противоположную угловому ускорению ε3 .
Главные векторы и главные моменты сил инерции показаны на рис. 6.8.
Определим кинематические соотношения между скоростями точек систе-
мы и выразим их через скорость VC центра масс катка 2. Каток 2 катится по не-
подвижной поверхности без скольжения. Мгновенный центр скоростей катка находится в точке K касания катка с поверхностью (см. рис. 6.7). В этом случае
угловая |
скорость |
катка |
2 |
|
|
ω |
2 |
= |
VC |
= |
VС |
. |
|
Скорость точки А катка 2: |
||||||||||||||||||||||||
|
|
СK |
r |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
V |
A |
= w |
2 |
× AK = w |
2 |
(R |
|
- r )=V |
|
|
R2 − r2 |
. Скорость точки Е блока 3 равна скоро- |
||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
2 |
|
C |
|
|
r2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
сти точки А катка 2, VE =VA . Тогда угловая скорость блока 3: |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ω = |
VE |
|
= |
VA |
= V |
|
(R2 − r2 ) |
. |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
R3 |
|
|
R3 |
|
|
|
|
C |
R3r2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Скорость груза 1 равна скорости точки D катка 2: |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
V = V |
D |
= w |
2 |
× DK = w |
2 |
(R + r ) = V |
|
(R2 + r2 ) |
. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
C |
|
|
r2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Соотношения между ускорениями определяются путем дифференцирова- |
||||||||||||||||||||||||||||||||||||
ния установленных кинематических равенств: |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
a = a |
C |
(R2 + r2 ) |
, |
ε |
2 |
= |
aС |
, |
|
ε |
3 |
= a |
C |
|
(R2 − r2 ) |
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
r2 |
|
|
|
|
|
|
|
|
|
|
r2 |
|
|
|
|
|
R3r2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Выразим кинематические равенства между скоростями в дифференциаль132
