KS_tema_9 (1)

После приведения подобных в правой части этого выражения, оно приобретает вид

ln kt ln 1 ln(1 ) (1 ) ln kt

Теперь осталось приравнять коэффициенты при одинаковых функциях в правой и левой части выражения:

ln 1 ln(1 )

(1 ) .

Отсюда,

тоже находится единственным образом. Таким образом, мы доказали, что наша догадка о виде функции V () была верной. Более того мы её точно знаем.

Из (**) и (***) следует, что оптимальное правило для капитала имеет вид

kt 1 kt .

Значит, оптимальное правило для выбора потребления (из ct kt kt 1 ) есть

ct (1 )kt .

То есть оптимальные потребление и инвестиции (которые при полном выбытии капитала совпадают с количеством капитал) составляют постоянную во времени долю выпуска.

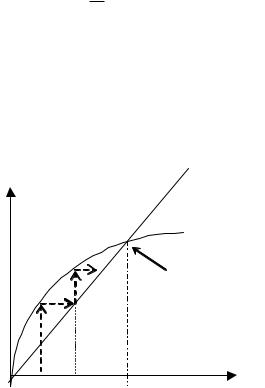
Уравнение движения равновесного капитала можно графически представить на Рис. 9.1.

И графически (из Рис 9.1), и алгебраически (с помощью уравнения движения равновесного движения капитала (***)) легко показать, что для любого положительного значения начального капитала, динамика модели приводит к устойчивому значению капитала kss , которое находится из (***) (когда kt 1 kt kss ), как

1

kss ( )1 .

То есть эта экономика не характеризуется долгосрочным ростом, а сходится к устойчивому состоянию, в котором капитал, потребление и выпуск постоянны во времени.

Рис. 9.1. Графический поиск устойчивогосостояния в моделиоптимального роста

Имея значения капитала в устойчивом состоянии, легко посчитать устойчивый уровень потребления и выпуска, которые, соотвественно, равны

9.2.3 Характеристика оптимального решения задачи, записанной в функциональной

форме

Если функция V () в (9.4) дифференцируема (условия, при которых она дифференцируема установили Бенвенисте и Шейнкман (1979) ) и вогнутая, решение задачи социального планирования можно характеризовать при помощи условий первого порядка.

308 Методы решения задач динамической оптимизации

k0 - задано.

Тогда условия первого порядка для задачи максимизации, записанной в правой стороне

(9.9), имеют вид

Тем не менее, не зная V () , мы не можем знать V () и не можем решить уравнение

(9.10) относительно оптимального выбора kt* 1 . Поэтому необходимо ещё одно условие оптимального решения, следующее из (9.10), дающее вид функции V () . Это условие можно получить, продифференцировав обе части выражения (9.10) по переменной состояния kt , предварительно предположив, что в правую часть (9.10) уже подставлено оптимальное правило поведения kt* 1 (kt ) , то есть

V (kt ) u f (kt ) (1 )kt kt* 1 (kt ) V (kt* 1 (kt )) .

Используя Теорему об огибающей, мы получаем

Чтобы понять, как получено (9.11), надо понять теорему об огибающей.

Предположим, что унас есть

и y* (x) оптимальной правило, которое максимизирует правую часть (9.12), то есть

Итак, решение задачи социального планирования, то есть Парето оптимальное решение, а следовательно, и набор последовательностей для потребления и капитала,

соответствующий равновесному решению в силу выполнения первой и второй теорем благосостояния, полностью задан условиями (9.15), (9.5), (9.6) для любого периода t :

u (ct ) f (kt 1 ) (1 ) u (ct 1 )

ct kt 1 f (kt ) (1 )kt k0 - задано.

Используя эти условия, можно без труда посчитать устойчивое состояние

(динамическое равновесие) модели, kt kss , t :

1

f (kss ) 1 .

То есть равновесное количество капитала в устойчивом состоянии зависит только от коэффициента дисконтирования полезности и от коэффициента выбытия капитала.

Основные понятия Темы 9

Задача динамической оптимизации в непрерывном времени.

Переменная контроля. Переменная состояния. Закон движения переменной состояния.

Гамильтониан. Условия трансверсальности.

Гамильтонианы текущего и приведенного значения целевой функции.

Задача динамической оптимизации в дискретном времени.

Модель оптимального роста.

Задача социального планирования.

Задача в последовательной форме.

Задача в функциональной форме.

Уравнение Беллмана. Переменные контроля. Переменные состояния.

Неподвижная точка сжимающего отображения.

Метод «Угадай, но проверяй».

Итеративно-аналитический метод.

Итеративно-численный метод.

Теорема об огибающей.

Литература к Теме 9

Основная:

Vinogradov, V.1999, A cook-book of mathematics, CERGE-EI lecture notes, CERGE-EI Stokey, N, Lucas, R. and E. Prescott, 1989, Recursive methods in economic dynamics, Harvard University Press