Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет им. H.Э.Баумана

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

metod_ukaz_3_semestr_new

.pdf

Скачиваний:

Добавлен:

23.03.2016

Размер:

2.15 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 44

Обратим внимание читателя на появление еще одной постоянной интегрирования C3 . Это

легко понять, если заметить, что исходная система уравнений (3.22) – (3.26) содержит три диф-

ференциальных уравнения первого порядка. В начальный момент времени ток IL через катушку

индуктивности равен	BlC2		+ C , т. е. определяется значениями двух постоянных интегрирова-

	ω	0 L	3

ния.

Располагая зависимостями от времени для тока через конденсатор и тока через катушку ин-

дуктивности, по уравнению (3.24) после необходимых преобразований получаем зависимость тока через перемычку:

I= mω0 (BlC2 cos ω0 t − E sin ω0 t ) + C3 .

B 2 l 2

Начальное значение тока через перемычку составляет

I (0 ) = m ω 0 C 2 + C 3 .

B l

Таким образом, все искомые переменные задачи определены в общем виде (с точностью до определения констант интегрирования). При выводе зависимости скорости перемычки от вре-

мени пришлось дифференцировать исходное уравнение (3.26), при этом в окончательном ре-

зультате исчезла постоянная величина ускорения свободного падения g. Необходимо убедиться,

что полученное решение действительно удовлетворяет дифференциальному уравнению для скорости перемычки. Проверка этого условия (оно должно выполняться для произвольного мо-

мента времени) приводит к соотношению

C3 = − gm .

Итак, постоянную интегрирования С1 мы определили единственным образом, постоянную интегрирования С3 также определили единственным образом. Постоянная интегрирования С2

пропорциональна электрическому току через конденсатор в начальный момент времени, она же участвует в формировании начального тока через катушку индуктивности и, таким образом, в

формировании начального тока через перемычку. Формально ее значение может быть произ-

вольным. Физически допустимыми являются начальные условия, позволяющие однозначно оп-

ределить значение постоянной интегрирования С2.

По условию задачи известно, что ток через перемычку в начальный момент времени равен нулю. Приравнивая выражение для I(0) нулю, получаем

C 2 = ω 0 .

После этого решение задачи приобретает окончательный вид:

υ(t) =

sin ω t −

(1 − cos ω t);

ω0

Blg

q(t) = −C

sin

ω0t + E cos ω0t ;

ω0

IC (t) = C(−Blg cos ω0t + Eω0 sin ω0t);

(t) =

Blg

cos ω t −

sin ω t −

;

Lω2

Lω

(1 − LCω2 )

Blg

I (t) =

cos ω0t − E sin ω0t

−

Lω0

ω0

Особенностью рассматриваемой задачи является то, что при ее решении потребовалось ус-

тановить законы изменения во времени заряда конденсатора, тока через конденсатор и тока че-

рез катушку индуктивности. Заметим, что в практически интересных случаях задание началь-

ных условий для параметров сложной электрической цепи может представлять определенные трудности.

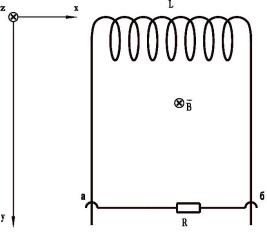
Задача 3.2. По двум гладким медным шинам скользит перемычка массой М, закон движения которой задан функцией y(t ) = a exp(−nt ) , где а и n — постоянные величины. Сопротивление перемычки равно R , поперечное сечение S, концентрация носителей заряда (электронов) в про-

воднике перемычки равна n0 .

Рис. 3.9

Сверху шины замкнуты электрической цепью, содержащей индуктивность L в соответствии с рис. 3.9. Расстояние l между шинами является постоянной величиной. Система находится в однородном переменном магнитном поле с индукцией Bz (t ) = c exp(− mt ) , перпендикулярном плоскости, в которой перемещается перемычка, а параметры c и m в законе изменения индук-

ции магнитного поля являются постоянными положительными величинами. Сопротивление

шин, скользящих контактов, а также самоиндукция контура пренебрежимо малы. Ток I через

перемычку в начальный момент времени равен нулю.

Найти:

–закон изменения электрического тока во времени I (t);

–закон изменения напряженности электрического поля E(t ) в перемычке;

–силу Fy (t ), действующую на перемычку, необходимую для обеспечения заданного закона

движения;

– связь между силой Ампера, действующей на перемычку, и силой Лоренца, действующей на электроны в перемычке.

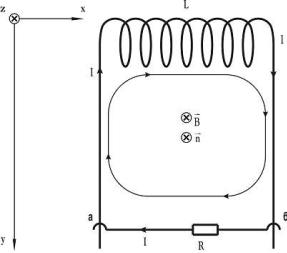
Рис. 3.10

Решение. Выберем направление единичной нормали	n так, чтобы
Решение. Выберем направление единичной нормали	n так, чтобы	n	↑↑ B , тогда поток век-

тора B будет положительным (рис. 3.10). Поток вектора B сквозь поверхность, натянутую на


контур аLба, равен Φ = ( B , n ) ly. ЭДС индукции, обусловленная изменением этого потока, в со-
ответствии с законом Фарадея
E		= −	d Φ	= −	d	[B		(t ) y (t )l ].	(3.34)
E	i	= −		= −		[B	z	(t ) y (t )l ].	(3.34)
	i		dt		dt		z
			dt		dt

Направление обхода рассматриваемого контура аLба согласуем с выбранным направлением вектора нормали n правилом правого винта. Тогда уравнение Кирхгофа (3.11) применительно к данной задаче примет вид

Ei	−	LdI	= IR.	(3.35)

		dt

Следует отметить, что в соотношении (3.35) ток I положительный, поскольку выбран так,

что его направление совпадает с направлением обхода контура аLба (см. рис. 3.10). Так как в

условии задачи заданы закон движения перемычки y(t ) = a exp(−nt )	и закон изменения магнит-
ного поля Bz (t ) = c exp(− mt ) , значение ЭДС индукции в соответствии с законом (3.1) равно
Ei =a l c(m + n) exp[−(m + n)t ].	(3.36)

Тогда для тока I (t ) , протекающего в контуре аLба, с учетом выражения (3.36) для Ei			полу-
чаем неоднородное дифференциальное уравнение с начальным условием I (0) = 0 :
L	dI	+ IR =a l c(m + n) exp[−(m + n)t ].	(3.37)

	dt

При решении однородного уравнения (3.37) воспользуемся методом Лагранжа. Запишем это

решение в форме

I (t) =

−

A(t ) exp

t . (3.38)

Подставим (3.38) в исходное уравнение (3.37) и найдем значение A(t) :

al c(m + n)

A(t ) =

exp

− (m + n) t

+ D.

− (m + n) L

Тогда общее решение уравнения (3.37) примет вид

a l c(m + n)

I (t ) = D exp

−

exp{[−(m + n)]t} . (3.39)

R − (m + n) L

В этом выражении значение константы D определим из начального условия I (0) = 0 :

D = −

a l c(m + n)

R − (m + n)L

Частное решение уравнения (3.37) с нулевым начальным условием имеет вид

alc(m + n)

I (t ) =

exp [−(m + n)t ]− exp

−

(3.40)

( R − (m + n) L)

Динамическое уравнение движения перемычки в проекции на ось Oy (аналог уравнения

(3.20)) в рассматриваемом случае выглядит следующим образом:

M	dυ y	= Mg + I l B + F (t), (3.41)

	dt	z	y

где I (t ) определяется зависимостью (3.40), а Fy (t)			— проекция на ось Oу управляющей силы,

действующей на перемычку. Из заданного в условиях задачи закона движения перемычки най-

дем производную по времени от проекции на ось Oy скорости перемычки:

dυ y = a n2 exp(−nt ) . dt

Тогда проекция управляющей силы Fy (t) из уравнения (3.41) с учетом последнего соотношения будет равна


	2		2		c2 al 2 (m + n)			R
Fy (t) = M a n		exp(−nt) − Mg − I l Bz = M a n		exp(−nt ) − Mg −		exp[−(2m + n)t ] − exp	−		− m t
Fy (t) = M a n		exp(−nt) − Mg − I l Bz = M a n		exp(−nt ) − Mg −		exp[−(2m + n)t ] − exp	−		− m t
					R − (m + n)L			L

Плотность тока в перемычке определяется зависимостью

j =	I (t)	,	(3.42)

	S

где S — площадь поперечного сечения проводника.

Напряженность электрического поля в перемычке определяем из закона Ома в дифференци-

альной форме

E =

= jρ

(3.43)

уд

где ρуд

— удельное сопротивление медной перемычки (справочное значение, см. [6]).

Среднюю скорость u направленного движения электрических зарядов,

образующих элек-

трический ток, находим из уравнения

u ,

j =

где

— модуль заряда электрона; n0 — объемная концентрация носителей заряда. В этом

случае справедливо соотношение

u =

(3.44)

n 0

где плотность тока j в перемычке определена зависимостью (3.42), модуль заряда электрона

e = 1, 6 10−19 Кл. Тогда полная скорость носителей зарядов (электронов)

υ = u + υп ,

где υп — скорость движения перемычки, при этом

υп y = dy / dt = −an exp(−nt )

— проекция скорости движения перемычки на ось Oy.

Сила Лоренца, которая действует на заряд, определяющий электрический ток, имеет вид

(3.45)

[υ

× B ] =

[( u

+ υ

) × B ] =

[ u

× B ] +

[υ

× B ]

Отметим, что векторы первого и второго слагаемых в соотношении (3.45) взаимно перпен-

дикулярны. Тогда

F =	e
F =	e	([ u	× B])2	+ ([υ	п	× B])2 .
л					п

Сила Лоренца, действующая на все носители зарядов,

F * = F S l n		= S l n	e						(3.46)
F * = F S l n		= S l n	e	[ u	× B] 2	+ [υ	п	× B])2 .	(3.46)
л	0	0					п

Сила Ампера, действующая на перемычку,

Fa = I l Bz .

Отношение этих сил с учетом соотношений I = jS , j = n0 e u после соответствующих пре-

образований равно

I l B

u SlB

≤ 1

S l n0

[ u

× B]2

+ [υп

× B]2 S l n0

[ u

× B]2

[υп

× B]2

1 +

В рассмотренных задачах закон электромагнитной индукции играет существенную роль.

Электродинамическое уравнение (второй закон Кирхгофа), полученное с помощью этого зако-

на, входит в общую замкнутую систему дифференциальных уравнений. Учет начальных усло-

вий позволяет найти единственное решение поставленной задачи, обладающее физическим смыслом.

ПРИЛОЖЕНИЕ

ОБЩИЕ ВЫРАЖЕНИЯ ДЛЯ ОПЕРАТОРОВ grad, div, rot, 2

Ортогональная криволинейная система координат ( x1, x2 , x3 ):

gradU =

∂U

h1 ∂x1

h 2 ∂x2

3 ∂x3

∂

div A =

(h2 h3 Ax1 ) +

(h1h3 Ax2 ) +

(h1h2 Ax3

)

h1h2 h

∂x2

∂x3

∂x1

h1e1

h2e2

h3e3

∂

rot A

h1h2 h3

∂x1

∂x2

∂x3

h1 Ax

h2 Ax

h3 Ax

(П.1)

(П.2)

(П.3)

∂

h h

∂U

∂

h h

∂U

∂

h h ∂U

2U =

2 3

1 3

(П.4)

h h h

∂x

h ∂x

∂x

h ∂x

∂x

h ∂x

1 2 3

— вектор-функция; (e1 ,

e2 , e3 )

Здесь U — скалярная функция; A{Ax

, Ax

, Ax }

— единичные ба-

зисные векторы; (h1 , h2 , h3 ) — метрические элементы (коэффициенты Ламе).

Прямоугольные координаты:

x1 = x, x2 = y, x3 = z; h1 = 1, h2 = 1, h3 = 1;

(П.5)

= i ; e = j ;

e = k .

Цилиндрические координаты:

x1 = r, x2 = ϕ, x3 = z; h1 = 1, h2

= r, h3 = 1;

(П.6)

= e ;

e = e ;

= e .

Связь с прямоугольными координатами:

x = R cos ϕ; y = r sin ϕ; z = z.

Координатные поверхности:

цилиндры r = const, плоскости ϕ = const,

плоскости z = const .

Сферические координаты:

x1 = r,		x2 = θ,		x3 = ϕ;			h1 = 1, h2	= r, h3	= r sin θ;
e	= e ;	e	= e		;	e = e .			(П.7)
1	r	2	θ			3	ϕ
Связь с прямоугольными координатами:
x = r sin θ cos ϕ,					y = r sin θ sin ϕ,			z = r cos θ.

Координатные поверхности:

концентрические сферы r = const, плоскости ϕ = const,

конусы θ = const .

ЛИТЕРАТУРА

1.Иродов И.Е. Электромагнетизм. М.: Физматлит, 2000.

2.Сивухин Д.В. Общий курс физики: В 5 т. Т. 3: Электричество. М.: Физматлит, 1996.

3.Детлаф А.А., Яворский Б.М. Курс физики. М.: Высш. шк., 2000.

4.Тамм И.Е. Основы теории электричества. М.: Наука, 1989.

5.Савельев И.В. Курс общей физики: В 5 т. Т. 4: Электричество. М.: Физматлит, 1998.

6.Физические величины: Справ. / Под ред. И.С. Григорьева, Е.З. Мелихова. М.: Энерго-

атомиздат, 1991.

<<< < Предыдущая 1 2 34 / 44

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
02.05.2019946.18 Кб3METODIChKA_Romanenko.doc
#
10.02.20151.85 Mб73MetodUkazначерт.pdf
#
24.11.2019199.17 Кб4Metod_ukazania.doc
#
10.02.2015262.74 Кб20metod_ukazania_stud-bakalavram_kurs_rab.pdf
#
09.02.20152.16 Mб19metod_ukaz_3_semestr_new.pdf
#
23.03.20162.15 Mб7metod_ukaz_3_semestr_new.pdf
#
10.02.20152.44 Mб19Metricheskie zadachi.pdf
#
09.02.2015285.88 Кб22Met_rek_po_vyp_KR_EONP_EP_2013 (1).docx
#
10.11.2019330.75 Кб3MGTU_UMK_kursovaya.doc
#
10.02.201510.05 Mб36mmt-virtreal_red.PDF
#
09.02.2015109.57 Кб5mnoshtext.doc