
Golovko
.pdf
x2 = A(x + 1)(x2 x + 1) + B(x2 x + 1) + (Cx + D)(x2 + 2x + 1):
Приравнивая коэффициенты при всех степенях, получаем систему (последнее равенство можно было не писать, раскрывая скобки сразу в исходном урав-
нении):
x3 : 0 = A + C;
x2 : 1 = B + 2C + D; x1 : 0 = B + C + 2D; x0 : 0 = A + B + D;
решая которую находим A = 31 |
, B = C = 31 |
, D = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
Таким образом, |
1 |
|
|
|
dx |
|
1 |
|
|
|
dx |
|
|
1 |
|
|
|
|
x |
|
|
|
1 |
|
|
|
|
1 |
|
|
|||||||||||
|
RR |
|
|
x2 |
|
|
|
R |
|
|
|
R j |
|
|
|
R |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
R (x |
2 ) |
|
4 |
x+1 |
|
|
|
|
j |
|
|
|
|
|
|
|
|
3 3 |
|
3 |
|
|
|
|||||||||||||
|
|
(x+1)(x3+1) dx = 3 |
|
|
+ 3 |
|
|
(x+1)2 + 3 |
|
|
x2 x+1 dx = 3 ln jx + 1j |
3(x+1) + |
||||||||||||||||||||||||||||||
1 |
|
2x 1 |
1 |
|
|
dx |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
2 |
|
|
1 |
|
|
2x 1 |
|
|
||||||||
6 |
|
x2 |
|
x+1 |
dx+ |
6 |
|
|
1 |
2+ 3 |
|
= |
|
3 ln x+1 |
|
|
3(x+1) |
+ |
6 ln(x |
|
|
x+1)+ |
p |
|
arctg |
|
p |
|
|
+C: |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
2. Метод Остроградского (обобщенный)
Если в разложении знаменателя рациональной дроби на линейные и квадратные множители без корней несколько кратных множителей (особенно квадратичных), то метод неопределенных коэффициентов приводит к очень длинным выкладкам. В этом случае можно воспользоваться (обобщенной) формулой Остроградского, которая справедлива для любой правильной рациональной функции:
Z |
Q(x)dx = |
Q1(x)+ |
x |
|
a1 |
+ : : : x |
|
as |
+ x2 + p1x + q1 |
+ : : : x2 + ptx + qt dx; |
||||
|
|
Z |
|
|
|
|
|
|
|
|
||||
|
P (x) |
P1(x) |
|
|
A1 |
|
|
As |
|
B1x + C1 |
|
Btx + Ct |
||
где P и Q многочлены из утверждения в начале параграфа, |
Q1 много- |
|||||||||||||
член с теме же неприводимыми множителями, что и Q, только в cтепенях, на единицу меньших, P1 многочлен, степень которого ниже степени многочлена Q1. Для отыскание неопределнных коэффициентов (в многочлене P1 è â ñëà-
гаемых второго интеграла), следует продифференцировать обе части формулы Остроградского.
Замечание. Также как и в первом методе, количество неизвестных коэффициентов равно степени знаменателя.
Замечание. Общий метод Остроградского можно найти, например, в [1] ( 2).
|
|
|
|
Найти интеграл R |
dx |
|
|||
Решение. |
|
(x2+1)2 |
|
||||||
Задача 2.5. |
|
|
|
|
|
. |
|||
По формуле Остроградского |
|
|
|||||||
R |
dx |
|
Ax+B |
|
R |
Cx+D |
|
|
|
(x2+1)2 = |
2 |
|
+ |
x2+1 dx. |
|
|
|||
|
x2+1 |
|
|
|
|||||
Продифференцировав последнее равенство, получаем:
1 |
|
A(x +1) 2x(Ax+B) |
Cx+D |
|
(x2+1)2 |
= |
|
(1+x2)2 |
+ x2+1 . |
Таким образом,
1 = A(x2 + 1) 2x(Ax + B) + (Cx + D)(x2 + 1) = Cx3 + (A 2A + D)x2 + ( 2B + C)x + A + D.
11
Приравнивая коэффициенты при всех степенях, получаем систему:
x3 : |
0 |
= C |
|
2 |
|
|
= A + D; |
x1 |
: |
0 |
|
x0 |
: 0 |
= 2B + C; |
|
x |
: |
1 |
= A + D; |
решая которую находим B = C = 0, A = D = 1 |
|||||||||||
Таким образом, |
|
|
|
|
|
|
|
2 . |
|||
|
1 |
|
dx |
|
x |
|
1 |
||||
1 |
|
x |
|
|
|
|
|||||
R |
|
dx = |
|
+ |
|
R |
|
= |
|
+ |
2 arctg x + C. |
(x2+1)2 |
2(x2+1) |
2 |
x2+1 |
2(x2+1) |
|||||||
12

3. Интегрирование тригонометричеких и гиперболических функций
В этом параграфе основное внимание будет уделено интегрированию тригонометрических функций. Гиперболические функции интегрируются аналогич- ными методами.
Замечание. Для преобразования выражений с гиперболическими функциями удобно использовать формулы:
ch2 x sh2 x = 1; ch2 x = 12 (ch 2x + 1); sh2 x = 12 (ch 2x 1);
2ch x ch y = ch (x + y) + ch (x y);
2sh x sh y = ch (x + y) ch (x y);
2sh x ch y = sh (x + y) + sh (x y).
В предыдущем параграфе был приведен метод интегрирование рациональных функций. Иногда интегралы от тригонометрических и гиперболических функций с помощью замены можно свести к интегралам от рациональных функций (или табличным интегралам), после чего можно использовать методы предыдущего параграфа.
Рассмотрим интегралы следующего вида:
Z
R(sin x; cos x)dx; |
(1) |
где R(x; y) рациональная функция двух переменных. В следующих случаях удобно использовать замены:
1)åñëè R( sin x; cos x) = R(sin x; cos x), òî t = cos x;
2)åñëè R(sin x; cos x) = R(sin x; cos x), òî t = sin x;
3)åñëè R( sin x; cos x) = R(sin x; cos x), òî t = tg x.
Замечание. Замены 1) и 2) обычно приводят к более коротким выкладкам, чем замена 3).
Замечание. Замены 1) и 2) легко запомнить следующим образом: если одна из тригонометрических функций (sin x или cos x) входит в рациональную
функцию только в нечетной степени, то другую следует заменить на t.
Интегралы (1) всегда можно свести к интегралам от рациональных функций с помощью замены t = tgx2 (универсальной тригонометрической подстановки ),
òàê êàê ïðè ýòîì |
|
|
|
|
|||
sin x = |
2t |
; cos x = |
12 t2 |
; dt = |
dx |
= t2+1 dx: |
|
2 |
2 x |
||||||
|
t +1 |
t |
+1 |
|
2 cos 2 |
2 |
|
Подстановка t = tgx |
часто приводит к громоздким вычислениям, поэтому |
||||||
|
|
2 |
|||||
прибегать к ней следует только тогда, когда не видно других путей к вычислению интеграла.
Замечание. Все указанные выше замены сводят интегралы (1) к интегра-
лам от рациональных функций.
Задача 3.1. Найти интеграл R sin3 x cos4 xdx.
Решение.
13

|
Так как подынтегральная функция обладает свойством |
R( sin x; cos x) = |
||||||||||||||||||||
|
R(sin x; cos x), используем замену t = cos x. При этом dt = |
2 |
|
sin xdx è |
|
|
||||||||||||||||
t4Rdt = t7 |
|
t5 |
+ C = |
7R |
|
|
|
5 |
|
+ C. |
R |
|
|
|
R |
t6dt |
|
|||||
R |
sin |
7 cos |
5 |
= |
7 |
sin |
|
x |
5cos |
x( sin xdx) |
= (1 t |
)t |
dt = |
|
|
|
||||||
|
|
|
|
|
cos |
x |
|
cos |
x |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
2 |
|
|
8, и для того, чтобы найти интеграл от |
|||||||||||
|
Замечание. В случае использования в задаче 3.1 замены |
t = tg |
2 |
знаме- |
||||||||||||||||||
натель оказался бы равным |
|
(t |
|
+ 1) |
|
|
|
|
|
|
|
|
||||||||||
полученной рациональной функции, пришлось бы проделать громоздкие вы- числения.
|
|
|
|
|
|
|
|
|
|
Найти |
|
|
|
|
|
R |
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение. |
|
|
|
x |
|
|
4 sin x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Задача 3.2. |
|
|
|
|
интеграл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Делаем замену t = tg 2 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4(t 41 ) |
|
|||||||||||||||||||
R |
|
|
dx |
|
4Rtg |
|
|
|
2dt |
|
|
|
|
|
R |
|
dt |
|
|
|
|
1 |
R |
|
|
dt |
|
1 |
|
4 |
|
|
||||||||||
|
2 |
|
|
|
|
x2 1 |
t +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
sin x = |
4+4t2 |
|
|
2t = 2 |
|
1 2 |
15 |
= 2 |
p arctg |
p |
+ |
||||||||||||||||||||||||||||||
4 |
|
|
|
2 |
|
|
|
2t |
= 2 |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
(t |
+1) 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(t |
|
4 ) |
+ 16 |
|
15 |
|
15 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
C = |
p |
|
arctg |
|
p |
|
|
+ C: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
15 |
|
15 |
|
|
|
|
|
4 ch x 3 sh x dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Задача 3.3. Найти интеграл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Решение, 1 способ. |
|
|
|
d(2 ch xR |
|
sh x) |
|
|
sh x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 ch x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
2 sh x ch x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
C, à |
|
2 ch x Rsh x dx = x + C, Ròî |
|
|
||||||||||||||||||||||||||||||||||||||
|
для нахождения исходного интеграла достаточно |
|||||||||||||||||||||||||||||||||||||||||
Òàê êàê |
|
2 ch x sh x dx = |
|
2 ch x sh x |
= ln j2 ch x |
sh xj+C = ln(2 ch x sh x)+ |
||||||||||||||||||||||||||||||||||||
|
|
|
2 ch x |
sh x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4 chRx 3 sh x |
= A2 sh x ch x + B 2 ch x sh x : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
представить его в виде линейной комбинации этих двух интегралов: |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
2 ch x sh x |
|
|
|
|
2 ch x sh x |
|
|
|
2 ch x sh x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Приравнивая в числителе коэффициенты при sh x и ch x, получаем систему:
3 = 2A B;
4= A + 2B;
решая которую находим A = 23 , B = 53 . Таким образом, исходный интеграл
ch x 3 sh x |
dx = |
2 |
R |
2 sh x ch x |
5 |
R |
2 ch x sh x |
2 |
ln j2 ch x sh xj+ |
5 |
R 42 ch x sh x |
3 |
2 ch x sh x dx+ |
3 |
2 ch x sh x dx = |
3 |
3 x+C: |
Замечание. Отметим, что прием, заключающейся в представлении подынтегральной функции в виде линейной комбинации двух функций, интералы от которых легко находятся, был использован в задаче 1.6.
Решение, 2 способ.
|
Так как подынтегральная функция обладает свойством R |
( sh |
x |
ch x) = |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
; 2 |
|
||
R(sh x; ch x), используем замену t = th x. При этом dt = |
|
dx = (1 t )dx è |
|||||||||||||||||||||||||||||||||||||
ch2x |
|||||||||||||||||||||||||||||||||||||||
исходный интеграл |
|
|
|
|
|
4 3 th x dx = |
|
|
|
4 3t 2 dt = |
|
|
4 3t |
|
dt: |
|
|
||||||||||||||||||||||
|
I = |
R |
4 ch x 3 sh x dx = |
R |
R |
|
R |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
2 ch x sh x |
|
|
|
|
|
|
|
|
2 th x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2 t)(1 t ) |
|
(t 2)(t 1)(t+1) |
|
|
|
|
||||||||||||||||
|
Представим полученную рациональную функцию в виде суммы элементар- |
||||||||||||||||||||||||||||||||||||||
ных дробей: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
4 3t |
|
= |
|
|
A |
+ |
|
|
B |
+ |
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
(t 2)(t 1)(t+1) |
|
t 1 |
|
|
|
|
t+1 |
|
|
t 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Таким образом, 4 3t = A(t + 1)(t 2) + B(t 1)(t 2) + C(t 1)(t + 1). |
1 |
|||||||||||||||||||||||||||||||||||||
B = |
67 , |
C = 32 |
, откуда |
|
|
|
|
|
|
|
|
|
|
|
|
t = 1, t = 1, t = 2, находим A = |
2 , |
||||||||||||||||||||||
|
Подставляя в последнее равенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
I = 21 |
R |
dt |
+ 67 |
R |
|
dt |
32 |
R |
|
|
dt |
+C = 21 ln jt 1j+ 67 ln jt+1j 32 ln jt 2j+C = |
||||||||||||||||||||||||||
|
t 1 |
t+1 |
|
t 2 |
|||||||||||||||||||||||||||||||||||
|
2 ln th |
x |
1 + 6 |
|
|
|
|
|
|
|
|
|
|
3 |
|
th x |
|
2 + C: |
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
j |
|
|
j |
|
7 |
ln |
j |
th x + 1 |
j |
|
2 ln |
j |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
||||||||||||
14

4. Интегрирование иррациональных функций
1. Интегралы вида
R x; |
ax + b |
|
p1 |
; : : : ; |
ax + b |
|
pn |
dx; |
(2) |
|
|
|
|
||||||
cx + d |
|
cx + d |
|
ãäå n 2 N, p1; p2; : : : ; pn 2 Q, a; b; c; d 2 R, ad bc 6= 0, использованием замены
ax+b = tm, где m общий знаменатель рациональных чисел p1; p2; : : : ; pn,
cx+d
приводятся к интегралу от рациональной функции.
|
|
Задача 4.1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
Решение. |
|
|
|
|
Найти интеграл R px+ px2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Так как подынтегральная функциÿ является рациональной функцией отно- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
, то используем замену x = tÍÎÊ(2;3) = t6. |
||||||||||||||||||||||||||||||||||||||||||||||||
сительно переменных x1 = x2 , x2 = x |
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Таким образом, dx = 6t5dt и исходный интеграл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
6t5dt |
|
|
|
|
|
|
|
|
|
|
t2dt |
|
|
|
|
|
|
|
|
|
|
t2 1 dt |
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
tdt |
6 |
dt |
|
|
|
|
|
|
|
dt |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
p |
x |
+ px2 = |
|
|
|
t3+t4 = 6 |
|
t+1 |
= 6 |
|
|
|
|
t+1 |
|
|
|
|
+ 6 |
|
|
|
|
|
t+1 |
= 6 |
|
|
|
|
|
|
|
|
+ 6 |
|
|
|
|
t+1 |
= |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
t2 |
R |
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
C = 3p3 |
|
|
|
|
|
6p6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p6 |
|
|
|
|
|
|
|
|
|
|
C. |
|
|
|
|
R |
|
|
|
R |
|
|
|
|
|
|||||||||||||||||||||||||||||||
6 |
+ 6 ln |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x |
|
+ 6 ln( |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 |
|
|
j |
R+ 1 + |
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
R |
|
|
+ 1) + R |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Замечание. 6 наименьшая степень t, которая позволяет избавиться от |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
иррациональности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
Рассматрим интеграл, который сводится к виду (2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
интеграл R |
|
p |
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
Задача 4.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти |
|
|
x 1 |
|
x+1 |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
px 1+px+1 dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Сократив дробь на |
|
|
p |
|
|
|
|
|
|
|
, |
сведем исходный интеграл к виду |
(2) |
: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
I = |
|
|
|
x 1 |
p |
dx = |
|
|
|
q |
|
dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
px 1+px+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qx+1 |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
ÄëÿRтого, чтобы св |
åñòи интеграл к интегралу от |
рациональной функции, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
сделаем замену t = |
|
|
|
|
|
x 1 . Таким образом, 2tdt = |
|
2dx |
|
|
|
|
= 2 |
|
1 t2 |
|
2 dx è |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4t(t 1) |
|
|
|
qx+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tdt |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x+1) |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
I = |
|
|
|
|
(t+1)(1 t)2(1+t)2 |
|
dt = 4 |
|
|
|
(t 1)(t+1)3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Представим полученную рациональную функцию в виде суммы элементар- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ных рациональных дробей: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
t |
|
|
|
|
|
= |
|
|
A |
|
|
+ |
|
|
B |
|
|
+ |
|
|
|
C |
|
+ |
|
|
|
|
D |
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
(t 1)(t+1) |
3 |
|
|
t 1 |
|
t+1 |
|
|
|
|
|
2 |
(t+1) |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(t+1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
Таким образом, t = A(t + 1)3 + B(t |
|
1)(t + 1)2 + C(t |
|
1)(t + 1) + D(t |
|
1). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
Подставляя в последнее выражение t = 1, получаем, что A = |
8 , подставляя |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
t = 1, получаем, что D = 21 |
; приравнивая в нем коэффициенты при t3, ïîëó- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
÷àåì, ÷òî |
0 = |
|
A |
+ |
B, откуда B |
= |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
t0 |
, получаем, что |
|
0 = |
A |
|
B |
|
C |
|
D, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 , à ïðè |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
откуда C = |
4 . Таким образом, исходный интеграл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
dt |
|
|
|
|
1 |
|
|
|
|
|
|
|
dt |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|||||||||||||||||||||||
|
|
I = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
4 |
|
|
|
|
|
|
|
+p2 |
|
|
|
|
|
|
|
|
|
|
= |
|
8 ln jt |
1j |
8 ln jt + 1j + |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
8 |
|
|
|
t 1 |
8 |
|
|
p |
t+1 |
|
|
|
|
|
(t+1)2 |
|
|
|
|
|
|
(t+1)3 |
|
|
4(t+1) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
C |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
x 1 |
|
x+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x+1 |
|
|
|
|
|
|
|
|
|
|
C: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
= |
|
|
|
ln |
|
R |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 + |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
4(t+1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
px 1+px+1 |
|
|
|
|
|
|
4(px 1+px+1) 4(px 1+px+1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Замечание. Мы рассмотрели интегралы, являющиеся рациональной функцией от x и фиксированной дробно-линейной функции в рациональных степе-
íÿõ.
2. Интегралы вида |
Z |
|
xm(axn + b)pdx;
15

где a; b 2 R, m; n; p 2 Q, причем a 6= 0, b 6= 0, n 6= 0, p 6= 0, называют интегра-
лами от дифференциального бинома. Эти интегралы сводятся к интегралам от рациональных функции в следующих трех случаях:
p целое число,
m+1
n целое число,
m+1 + p целое число.
n
В первом случае (это интеграл вида (2)) используется замена x = tN , ãäå
N общий знаменатель дробей m и n; во втором и третьем случаях соответственно замены axn + b = ts è a + bx n
p.
Замечание. Написанные выше подстановки называются подстановками Че- бышева. В остальных случаях интегралы от дифференциального бинома не выражаются через элементарные функции.
|
|
|
|
Задача 4.3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
Найти интеграл R x2 p3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
(x3+2)5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
Заметим, что это интеграл от дифференциального бинома с m |
|
|
|
, n = 3, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
p = |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m+1 |
+ p |
|
, то используем замену 1 + 2x 3 |
= 2. Таким |
|||||||||||||||||||||||||||||||||||||||||||||||||||
3 . Òàê êàê |
|
|
|
|
|
|
= t3 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
2 Z |
|
|
|
|
|
|
|
2 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
образом, 6x 4dx = 3t2dt (òî åñòü dx = 5 t |
x2 dt ) è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
31 dt = |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
= |
|
1 |
|
|
x 2(x3(1+2x 3)) 3 t2x4dt = |
|
|
1 |
|
|
x 3t 3dt = |
1 |
|
|
t |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x2 p3 (x3+2)5 |
|
2 |
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2t |
|
|
|
|||||||||||||||||||||
|
|
|
1R |
|
|
|
|
1 |
|
|
|
|
dt |
|
|
|
|
|
tR |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
R |
|
|
|
|
. |
|
|
|
|
R |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p1+2x 3 |
|
|
|
|
|
|
|
8 p3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
dt + |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
+ C = |
|
|
|
|
|
|
|
|
|
|
|
|
|
+ C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
4 |
|
4 |
|
|
|
|
t3 |
|
4 |
8t2 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1+2x 3)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3. Тригонометрические и гиперболические замены. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
R |
|
|
|
|
|
|
R |
|
|
|
|
Найти интеграл R pp |
2 |
|
|
2 |
|
|
|
|
|
|
, ãäå |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
Задача 4.4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Решение. |
|
|
|
|
|
|
x |
|
dx |
|
|
|
|
|
p > 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x = |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
Этот интеграл можно найти с помощью тригонометричекой замены |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
; ]. Тогда dx = p cos tdt, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
p sin t, ãäå t |
2 |
|
[ |
|
|
|
|
|
|
|
p2 |
|
x2 = |
p2 cos2 t = p cos t (òàê |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
à |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
êàê p cos t > 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
â ñèëó òîãî, ÷òî t 2 [ 2 ; 2 ]), p |
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
2 |
|
|
x |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2t |
|
p2 sin 2t |
|
|
|
|
p |
|
arcsin p |
|
|||||||||||
|
|
|
|
|
|
p2 x |
|
x2dx = p2 |
|
cos2 tdt = 2 |
|
(1+cos 2t)dt = |
|
|
|
+ |
|
|
|
|
|
+C = |
|
|
|
|
|
+ |
||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
2 |
|
4 |
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
p |
|
sin(2 arcsin |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
R p |
|
|
|
p |
|
|
|
+ C: |
|
|
|
|
|
R |
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
В следующих случаях удобно использовать следующие тригонометрические |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(и гиперболические) замены: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1) в интеграле |
|
R(x; |
p2 x2)dx замены x = p sin t, x = p cos t, x = p th t; |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
R R(x; p |
|
|
|
)dx замены x = |
p |
, x = p ch t; |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2) в интеграле |
x2 p2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
cos t |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
R R(x; p |
|
|
)dx замены x = p tg t, x = p sh t. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3) в интеграле |
x2 + p2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Эти замены |
|
позволяют избавиться от иррациональности и свести интеграл |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
R |
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
ê âèäó (1). |
|
|
|
|
|
|
|
|
Найти интеграл R |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
Задача 4.5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
1+px2+2x+2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
Выделяя полный квадрат в подкоренном выражении и используя замену |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x = t + 1, сводим исходный интеграл к указанному выше виду: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
I = |
|
|
|
|
|
|
|
dx |
|
|
|
|
= |
|
1+p |
dx |
= |
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
1+p |
|
|
|
|
|
|
1+p |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x2+2x+2 |
|
(x+1)2+1 |
|
|
t2+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Используем замену |
|
|
|
|
|
|
|
|
|
|
R |
; |
|
|
|
|
|
|
. Тогда dt = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
è |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rt = tg u, ãäå t |
2 |
|
|
|
|
cos |
u |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
16
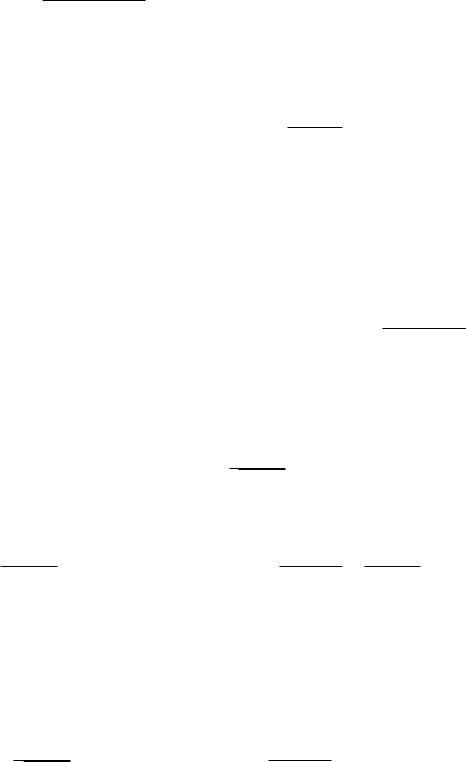
|
du |
|
|
du |
|
du |
|
|||||
I = |
cos2 u(1+p |
|
|
= |
|
|
|
|
= |
|
: |
|
cos2 u(1+ |
1 |
) |
cos2 u+cos u |
|||||||||
tg2u+1) |
||||||||||||
|
|
|
cos u |
|
|
|||||||
ÄëÿRвычисления |
последнего интеграла воспользуемся универсальной триго- |
|||||||||||||||||||||||||||||
|
|
|
R |
|
|
|
|
|
|
R |
cos u = 12 v2 |
|
|
|
|
|
|
|
|
|
(v2+1)du |
|
||||||||
нометрической подстановкой v = tgu |
|
|
|
|
dv = |
du |
= |
|
||||||||||||||||||||||
|
|
|
2 u |
|
|
|
2 , |
|||||||||||||||||||||||
а интеграл |
|
|
|
|
|
|
|
|
|
|
2 . Тогда |
|
v +1 , |
|
|
|
|
|
2 cos |
2 |
|
|
|
|
||||||
1 |
|
|
|
2dv |
|
|
|
|
|
v2+1 |
|
|
|
v2+1 |
|
R |
v2 |
+1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
I = |
|
|
|
|
|
|
= 2 |
|
|
|
|
|
|
|
dv = 2 |
|
|
|
|
dv = |
|
|
1 dv = |
|||||||
1 v2 |
|
2 |
1 v2 |
v2+1 |
(1 |
|
v2)2 |
+(1 |
|
v2)(1+v2) |
2 |
|
2v2 |
v2 |
|
|||||||||||||||
R |
v2+1 |
|
+ v2+1 |
|
R |
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|||||||||
R dv 2 R |
dv |
v2 1 |
= v ln
1 v
1+v
+ C = tg
arctg(x 1)
2
|
|
1+tg |
2 |
|
|
|
|
|
|
|
1 tg |
arctg(x 1) |
|
|
|
|
|
2 |
|
|
|||
|
ln |
|
|
|
|
|
+ C: |
|
|
|
arctg(x |
1) |
|
||
|
|
|
|
|
|
|
|
4. Для вычисления интегралов вида
|
|
Z |
|
ax2 + px + q ; |
|
|
(3) |
||
|
|
|
|
|
Pn(x)dx |
|
|
|
|
ãäå Pn многочлен степени n, |
|
p |
|
|
|
|
|
||
Z |
|
|
целесообразно воспользоваться формулой |
|
|||||
pax2 + bx + c = Q(x)pax2 + bx + x + Z |
pax2 + bx + c; |
(4) |
|||||||
|
|
Pn(x)dx |
|
|
|
|
|
dx |
|
где Q многочлен степени не выше, чем n 1, а некоторое число. Диффе- p
ренцируя обе части формулы (4) и затем умножая на ax2 + bx + c, получаем равенство многочленов, из которого находим и коэффициенты многочлена
Q.
Замечание. Этот метод аналогичен методу Остроградского (для вычисления интегралов от рациональных функций).
Замечание. Количество неопределенных коэффициентов в данном методе
на 1 больше степени многочлена в числителе. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Задача 4.6. |
Найти интеграл |
R |
|
2x2 3x |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Решение. |
|
px2 2x+5 dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
По формуле (4) |
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
R |
|
2x2 3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
px2 2x+5 dx = (Ax + B) x 2x + 5 + px2 2x+5 : |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
Продифференцировав последнее равенство, получаем |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
2x 3x |
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
x |
2 |
2x + 5 + (Ax + B) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
p |
|
|
= A |
|
|
|
2p |
|
|
|
+ |
p |
|
|
. |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
x2 2x+5 |
|
|
|
x2 2x+5 |
x2 2x+5 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2x2 3x = A(x2 2x + 5) + (Ax + B2)(x1 1)0+в правой. |
и левой части, полу- |
|||||||||||||||||||||||||||||||||||||||||||||||||||
Приравнивая коэффициенты при x , x и x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
чаем систему: |
|
|
|
|
|
|
x2 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
= 2A + B; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
3 = 3A + B; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x : |
|
0 = 5A B + ; |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
решая которую находим A = 1, B = 0, = 5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
Таким образом, |
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
2x2 3x |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||
1 +Rpx2 |
|
2x + 5 + C. |
|
2x + 5 |
|
5 |
R |
p |
|
|
|
= 2x x |
|
2x + 5 |
|
j |
x |
|
||||||||||||||||||||||||||||||||||
(x 1) |
2 |
+4 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
px2 |
|
2x+5 dx = 2x x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 ln |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5. Интегралы вида |
|
Z |
(x )kpax2 + bx + c |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17
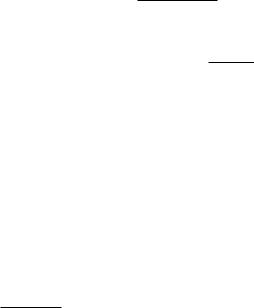
использованием замены t |
= |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
x приводятся к интегралам вида (3), причем |
||||||||||||||||||||||||||||||||||||||||||||||||||||
n = k 1. |
|
|
|
Найти интеграл R |
|
|
|
|
|
|
dx |
|
dx |
, |
x > |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Решение. |
|
|
|
(x+1)p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
x2+x+1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
Задача 4.7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Делаем замену t = |
1 |
|
. Ïðè ýòîì t > 0, x = 1 t t , dx = dtt2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
x+1 |
è |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
R |
|
|
dx |
|
|
|
|
|
R |
|
|
|
|
|
tdt |
|
|
|
|
|
|
|
x+2pxR2+x |
dt |
|
|
R |
|
|
|
|
dt |
|
|
|
|
|
||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
p |
2 |
|
|
|
|
|
t |
|
|
|
|
|
t |
|
|
|
1 |
+1 |
|
|
t+1 = |
|
|
|
2 |
x+14 |
|
||||||||||||||||||||||
|
|
(x+1)px2 |
+x+1 |
= |
|
t2 |
|
( |
1 t |
) |
2 |
+ 1 t |
+1 |
|
= |
pt2 |
|
|
( |
t |
|
1 |
) |
2+ 3 = |
|
|||||||||||||||||||||||||||
|
Замечание. После замены мы получили |
|
|
|
|
|
|
âèäà (3) ñ n = 0, |
|
|||||||||||||||||||||||||||||||||||||||||||
|
интеграл |
|||||||||||||||||||||||||||||||||||||||||||||||||||
ln t |
2 + |
|
t |
|
t + 1 + C = |
ln |
|
|
|
|
2(x+1) |
|
|
|
|
|
|
+ C = ln 1 x+2px2+x+1 |
+ C1. |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
на 1 меньшим, чем степень линейной |
|
части знаменателя, |
как и должно быть. |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
òî åñòü |
|
6. Интегралы вида |
|
|
|
|
|
|
|
|
Z |
|
(x2(+ px + q) 2m2+1 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ax + B)dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
ãäå p2 4q < 0, можно представить в виде линейной комбинации двух интегралов |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Z |
(x2 + px + q) |
2m2+1 |
|
|
|
|
|
è |
|
|
Z |
(x2 + px + q) 2m2+1 : |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(2x + p)dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Первый интеграл берется подстановкой |
u = x2 + px + q, а второй подстановкой Абеля t = |
|||||||||||||||||||||||||||||||||||||||||||||||||||
(p |
|
)0 = |
|
p |
2x+p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
x2 + px + q |
|
|
|
сводится к интегралу от многочленов. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
2x2+px+q
18

5. Задачи для самостоятельного решения
Найти интеграл (1 36). Основные методы интегрирования
1. |
R (x2 2)2dx. |
||||||||
2. |
R |
sin 3x sin 4xdx. |
|||||||
3. |
x2 cos x3dx. |
||||||||
|
R |
|
|
|
|
|
|
|
|
4. |
R |
|
2p |
x |
dx. |
||||
|
p |
|
|
|
|||||
|
x |
||||||||
5. |
pcos x sin7 xdx. |
||||||||
|
R |
|
|
|
|
|
|
|
|
6. |
R |
|
cos ln x+ln2 x dx. |
||||||
7. |
|
23x+2 dx. |
|||||||
|
|
|
|
|
|
|
|
x |
|
R
x 3x+5
R
8.x sin(2x + 1)dx.
9.R (x2 + x) sh 3xdx.
10. |
R |
arctg xdx. |
|
|
||||||||||||||
11. |
ln3 x |
pxdx. |
|
|
||||||||||||||
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
12. |
R |
cos 2x sh 3xdx. |
||||||||||||||||
13. |
x2arctg xdx. |
|
|
|||||||||||||||
14. |
R |
|
ln(4+th2 x) |
dx. |
|
|
||||||||||||
|
1+sh2 x |
|
|
|
|
|
|
|||||||||||
15. |
R |
x arcsin |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
x |
|
dx. |
|||||||||
px+1 |
|
|||||||||||||||||
|
R |
|
|
|
|
|
|
|
|
|
||||||||
16. |
R |
|
arcctg p |
x |
|
dx. |
|
|
||||||||||
|
p |
|
|
|
3 |
|
|
|
|
|
||||||||
|
x |
(x+1) 2 |
|
|
|
|
|
|
|
|
|
|
||||||
Интегрирование рациональных функций
|
R |
3 |
|
2 |
|
|
|
|
|
|
|
|
|
17. |
x 2 4x |
|
|
+1 |
dx. |
|
|
|
|
|
|||
|
x |
4x+3 |
|
|
|
|
|
|
|||||
|
|
2+5 |
|
|
|
|
|
|
|
||||
18. |
|
x |
|
|
|
dx. |
|
|
|||||
|
2 |
(x+2) |
|
|
|||||||||
|
R |
|
1) |
|
|
|
|
|
|
|
|||
|
(x x2+5x |
|
. |
|
|
|
|||||||
19. |
R |
|
dx |
|
|
|
|
|
|||||
(x 1)(x2+5) |
|
|
|
|
|
||||||||
|
2x3+6x2+3x 5 |
|
|
|
. |
|
|||||||
20. |
R |
|
+1)(x2+x+2) |
dx |
|
|
|||||||
|
(2xx3 |
|
x2+2x+2 |
|
|
|
. |
||||||
21. |
R |
x4 3x3+5x2 5x+2 |
dx |
|
|||||||||
22. R x5+x2 1 dx.
x6+2x4+x2
Интегрирование тригонометричеких и гиперболических функций
23. |
R sh3 x ch4 xdx. |
||
24. |
R |
dx |
|
sin2 x cos4 x |
. |
||
19

25. |
R sin2 x cos 3xdx. |
||
26. |
R |
dx |
|
2 sin x+cos x+5 . |
|||
Rtg x 5
27.2 tg x+1 dx.
Интегрирование иррациональных функций
dx
28. |
R |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
px5+ px3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
p |
|
|
|
|
|
|
|
|
|
dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
29 |
|
|
2x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
30.R |
|
|
|
|
x 1 |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
R |
5 |
|
|
|
x |
|
1)7(x |
|
2)3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
p3 |
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
31. |
R |
|
ppx+1 |
dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
32. |
|
|
|
|
|
|
|
xx |
|
|
dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
p2x4+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
33. |
|
|
x+1 |
dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
R |
|
px2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
34. |
R |
|
p |
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
x |
2+2x+5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
35. |
R |
|
|
2p |
|
|
|
|
, x > 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
x |
x2+4x+2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
36. |
|
|
|
|
|
|
4x+3 |
dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
R (x2+x+1) 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
ОТВЕТЫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1. |
x5 |
|
34 x3 + 4x + C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
2. |
sin2 x sin147x + C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
3. |
sin x3 |
|
|
|
+ C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4. |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
+ C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
ln 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos4 x + 73 sin2 x 31 p |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
cos6 x |
3 |
|
|
|
+ C. |
||||||||||||||||||||||||||||||||||||||||||
5. 2 |
|
|
|
|
|
|
cos3 x |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
15 |
|
|
11 |
|
||||||||||||||||||||||||||||||||||||||||||||||||
6. sin ln x + |
|
ln3 x |
|
+ C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
7. |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3x + 5) + |
|
13 |
|
|
2x 3 |
|
|
. |
|
|
|
|||||||||||||||||||||||||||
|
2 |
|
ln(x |
|
|
|
|
p |
11 |
arctg p |
11 |
+ C |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
8. |
x cos(2x+1) |
+ |
|
sin(2x+1) |
+ C. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
9. |
|
(9x2+9x+2) ch 3x 3(2x+1) sh 3x |
+ C. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
10. |
x arctg x |
ln(1+x2) |
+ C. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
11. |
|
2 |
|
|
x |
3 |
(9 ln3 x |
18 ln2 x + 24 ln x 16) + C. |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
27 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
12. |
|
2 sin 2x sh 3x+3 cos 2x ch 3x + C. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
13. |
|
x3 |
|
arctgx |
|
x2 |
|
|
ln(1+x2) |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
+ C. |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
6 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
14. |
th x ln(1 + th2 x) 2th x + 4arctg |
th x |
+ C. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
20
