2420-differencial-noe-ischislenie-funkciy-odnoy-peremennoy

3.ПРОИЗВОДНАЯ И ЕЕ ПРИЛОЖЕНИЕ

КИССЛЕДОВАНИЮ ФУНКЦИЙ

3.1. Производная функции в точке

ОПРЕДЕЛЕНИЕ 3.1. Пусть функция f(x) определена в U(x0) и х – произвольная точка этой окрестности. Если существует конечный

предел отношения f (x) − f ( x0 ) при х → х0, то функция называется x − x0

дифференцируемой в точке х0, а сам предел называется производной функции f(x) в точке х0 и обозначается f '(x0), т.е.

Обозначим x = x – x0 – приращение аргумента при переходе из точки х0 в точку х, а вызванное этим приращением приращение функции y = f(x0 + x) – f(x0). Тогда

f ′(x0 ) = lim

y

x→0 x

– предел отношения приращения функции при переходе из точки х0 в точку x0 + x к вызвавшему это приращение приращению аргумента

x, когда приращение аргумента стремится к нулю.

3.2. Непрерывность дифференцируемой функции

ТЕОРЕМА 3.1. Если функция f(x) дифференцируема в точке x0, то она непрерывна в этой точке.

Доказательство. Пусть существует

f (x) − f (x0 ) = f ′(x0 ) + o(1) при х → х0, x − x0

71

откуда получим, что

f(x) – f(x0) = (f '(x0) + о(1))(х – х0) → 0 при х → х0,

т.е.

lim f (x) = f (x0 ).

x→x0

Замечание. Непрерывность функции в точке не является достаточным условием ее дифференцируемости в этой точке. Например, f(x) = х непрерывна в точке х = 0, но

То есть функция не имеет производной в точке х = 0.

3.3. Дифференциал функции

Пусть функция у = f(x) дифференцируема в точке х0, т.е. существует

x часть приращения функции у = f(x) в точке х0 называется дифференциалом функции в точке х0 при приращении x и обозначается

df(х0; x) или df(х0) или df или dу.

Теперь приращение функции можно записать так:

y = f(x0 + x) – f(x0) = df(х0; x) + о( x) при х → 0.

Замечание. Для большей симметрии записи дифференциала приращение х обозначают dх и называют дифференциалом независимой переменной. Таким образом, дифференциал можно записать в виде

df(хо) = f '(x0)dх.

72

Если функция дифференцируема в каждой точке некоторого интервала, то ее дифференциал dy – функция от х и dx

dy = f '(x)dx.

Отсюда, в частности, получается выражение для производной

f ′(x) = dy dx

– отношение дифференциала функции к дифференциалу независимой переменной.

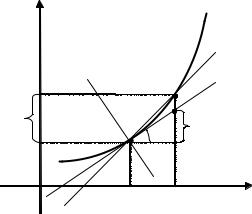
3.4.Геометрический смысл производной

идифференциала

Пусть функция определена в U(x0) и дифференцируема в точке х0.

ОПРЕДЕЛЕНИЕ 3.3. Касательной к графику функции у = f(x) в точке М0 называется предельное положение секущей L при х → 0.

Если функция дифференцируема в точке х0, то угловой коэффици-

из уравнения секущей, называется вертикальной касательной к графику функции в точке М0.

Нормалью к графику функции в точке М0 называется прямая, перпендикулярная касательной, проходящая через точку М0. Ее уравнение имеет вид

73

Из уравнения касательной, в частности, получим

у– у0 = f ′(x0)(х – х0) = df(х0)

–приращение ординаты касательной при переходе из точки х0 в точку х (рис. 3.1).

Рис. 3.1. Геометрический смысл производной и дифференциала

3.5.Физические приложения производной

идифференциала

1.Если S(t) – путь, пройденный материальной точкой за время t, то S'(t) – мгновенная скорость материальной точки, а ds = S'(t)dt – расстояние, которое прошла бы материальная точка за промежуток времени от t до t + dt, если бы она двигалась со скоростью, равной мгновенной скорости в момент t.

2.Если Q(t) – количество электричества, протекающего через поперечное сечение проводника в момент времени t, то Q'(t) = I – сила тока.

3.Если N(t) – количество вещества, образующегося в момент t в ходе химической реакции, то N'(t) – скорость химической реакции.

74

3.6. Правила дифференцирования

ТЕОРЕМА 3.2. (Дифференцирование суммы, произведения, частного.) Если функции f и g дифференцируемы в точке х, то в этой

75

= f (x + x) g(x) − f ( x) g(x) + f ( x) g( x) − f ( x) g( x + x) =

СЛЕДСТВИЕ. Если функция f(х) дифференцируема в точке х и С = const, то

ТЕОРЕМА 3.3. (Дифференцирование сложной функции.) Пусть

1)функция u = ϕ(x) дифференцируема в точке x0;

2)функция у = f(u) дифференцируема в точке u0 = ϕ(х0).

Тогда сложная функция у = f(ϕ(x)) дифференцируема в точке x0 и

fx′ (ϕ( x0 )) = fu′(u0 )ϕ′x ( x0 ).

Или, короче,

dy = dy du . dx du dx

Доказательство. Функция u = ϕ(x) дифференцируема в точке x0, следовательно, ее приращение при переходе из точки х0 в точку х представимо в виде

u = ϕ(x) − ϕ(x0) = ϕ'(x0) x + о( x) при x → 0.

Аналогично, функция у = f(u) дифференцируема в точке u0, т.е.

y = f(u) − f(u0) = f '(u0) u + о( u) при u → 0.

С учетом сказанного выше, последнее равенство можно преобразовать к виду

y = f(ϕ(x)) − f(ϕ(x0)) = f '(u0)(ϕ'(x0) x + о( x)) + о( u) =

= f '(u0)ϕ'(x0) x + f '(u0)о( x) + о( u),

а затем разделить на x:

76

Замечание. Правило вычисления производной сложной функции распространяется на композицию любого конечного числа функций. Например:

(f(ϕ(g(x))))' = f '(ϕ(g(x))) ϕ'(g(x)) g'(x).

ТЕОРЕМА 3.4. (Дифференцирование обратной функции.) Если функция у = f(x) непрерывна и строго монотонна на отрезке [x0 − δ, x0 + δ] и имеет производную f '(x0) ≠ 0, тогда обратная к ней функция

Доказательство. Пусть f(x) строго возрастает на отрезке [x0 − δ,

x0 + δ]. Обозначим α = f(x0 − δ), β = f(x0 + δ). Тогда на отрезке [α, β] определена обратная функция x = g(y), непрерывная и строго возрас-

77

4. Тригонометрические функции a) y = sin x, x R:

(sin x)′ = cos x.

б) y = cos x, x R:

(cos x)′ = (sin(π/2 – x))′ = cos(π/2 – x) (π/2 – x)′ = sinx.

в) y = tgx, х ≠ π/2 + πn, n Z:

5. Степенная функция y = xα, αR, x > 0:

(xα )′ = (eαln x )′ = eαln x (α ln x)′ = xα α = αxα−1 . x

6. Обратные тригонометрические функции Здесь воспользуемся теоремой о дифференцировании обратной

функции.

a) y = arcsin x, x (–1, 1), y (– π/2, π/2):

б) y = arcos x, x (–1, 1), y (0, π):

79

г) y = cthx, x ≠ 0:

3.8. Производная n-го порядка

ОПРЕДЕЛЕНИЕ 3.4. Пусть функция f(x) определена в Uδ(x0) и имеет производную f ′(x) в каждой точке этого интервала. Если в точке х0 существует производная от f ′(x), то она называется второй производной от функции f(x) в этой точке и обозначается f ′′(x0), или f (2)(x0).

80